Grundkenntnisse
1.
Mache einen Überschlag. Kreuze die Zahl an, die dem Ergebnis am nächsten liegt.

(1 Pkt.)
2.
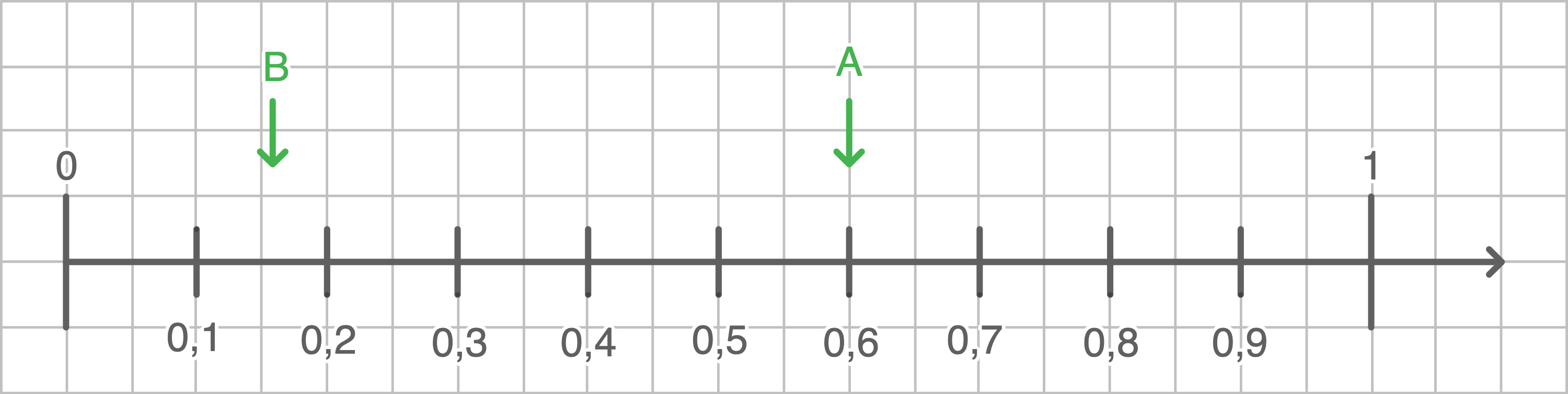
Markiere möglichst genau am Zahlenstrahl:


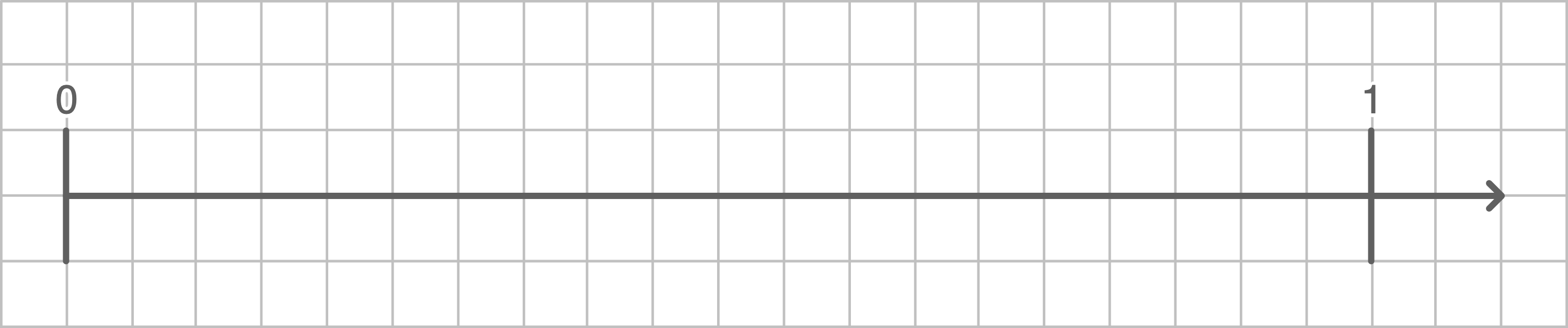

(1 Pkt.)
3.
Berechne die Differenz von  und
und 
(1 Pkt.)
4.
Eine Kiwi kostet  Eine Packung mit vier Kiwis wird für
Eine Packung mit vier Kiwis wird für  angeboten.
angeboten.
Luisa rechnet und sagt dann zur Verkäuferin: „Ich möchte 4 einzelne Kiwis.“
Warum? Begründe rechnerisch.
Luisa rechnet und sagt dann zur Verkäuferin: „Ich möchte 4 einzelne Kiwis.“
Warum? Begründe rechnerisch.
(1 Pkt.)
5.
Die einzelnen Würfel des Körpers haben eine Kantenlänge von 
Die vier grauen Würfel werden herausgenommen.
Um wie viel verändert sich nun die Oberfläche des Körpers?
verändert sich nun die Oberfläche des Körpers?
Die vier grauen Würfel werden herausgenommen.
Um wie viel
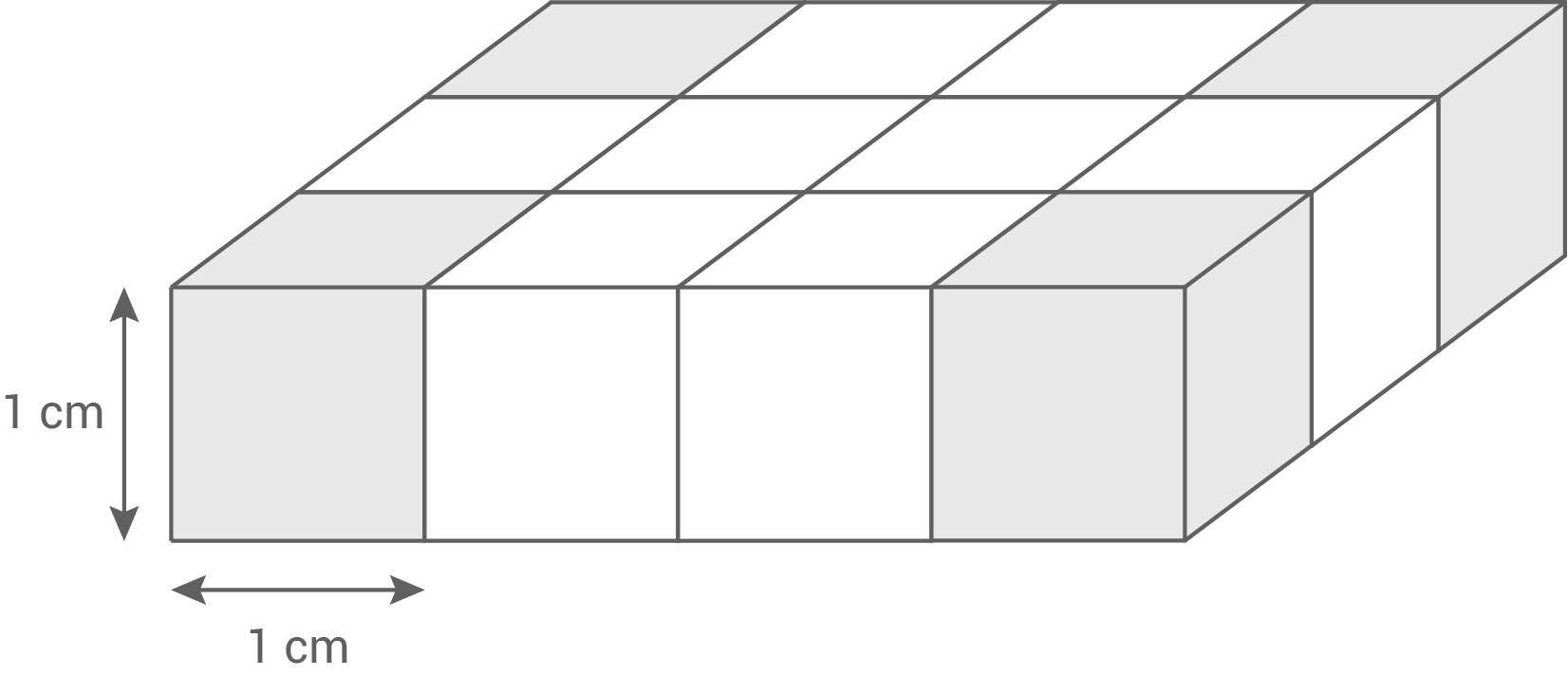
(1 Pkt.)
6.
Setze die Zahlenreihe um 2 Zahlen fort.


(1 Pkt.)
7.
Löse die Gleichung.

(1 Pkt.)
8.
Das Kreisdiagramm gibt das Ergebnis einer Wahl an.
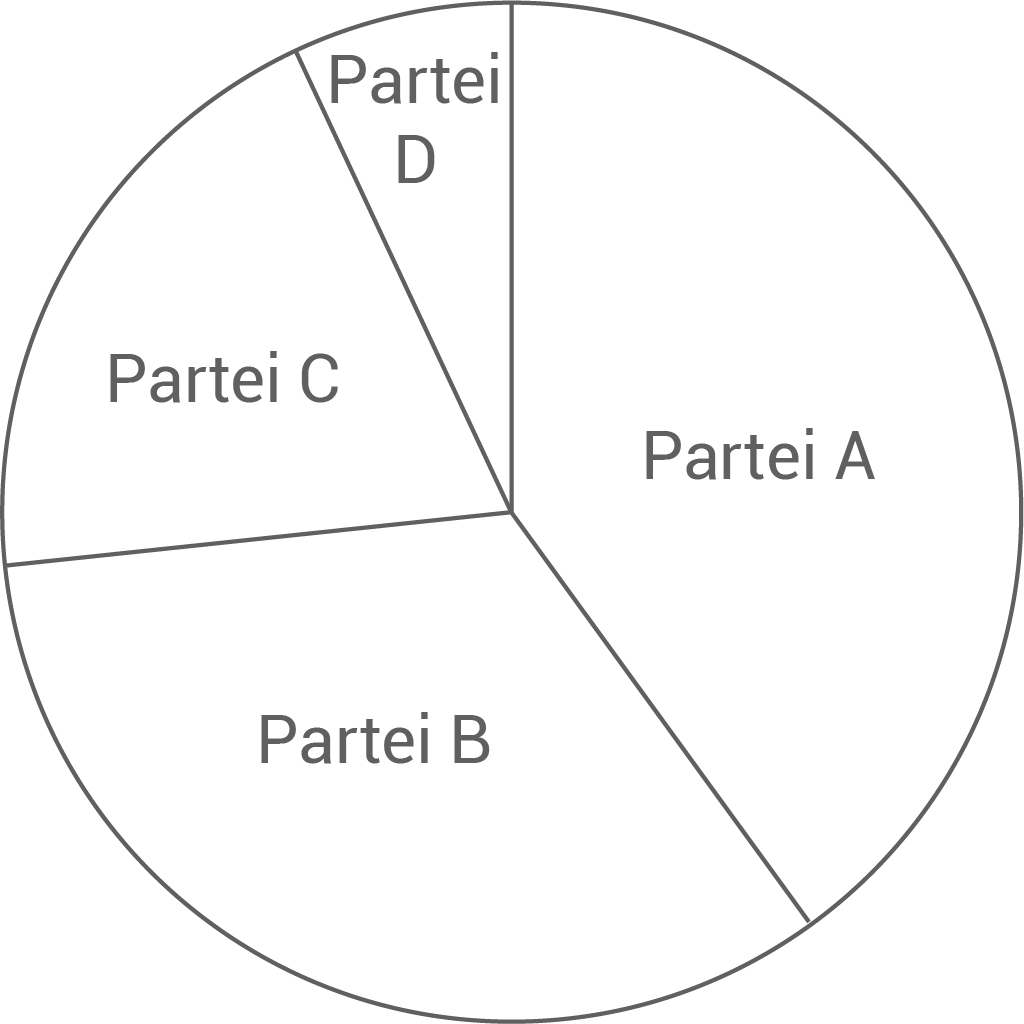 Wie viel Prozent der Wähler haben Partei C gewählt?
Wie viel Prozent der Wähler haben Partei C gewählt?

(1 Pkt.)
9.
Konstruiere folgendes Dreieck: 


(1 Pkt.)
10.
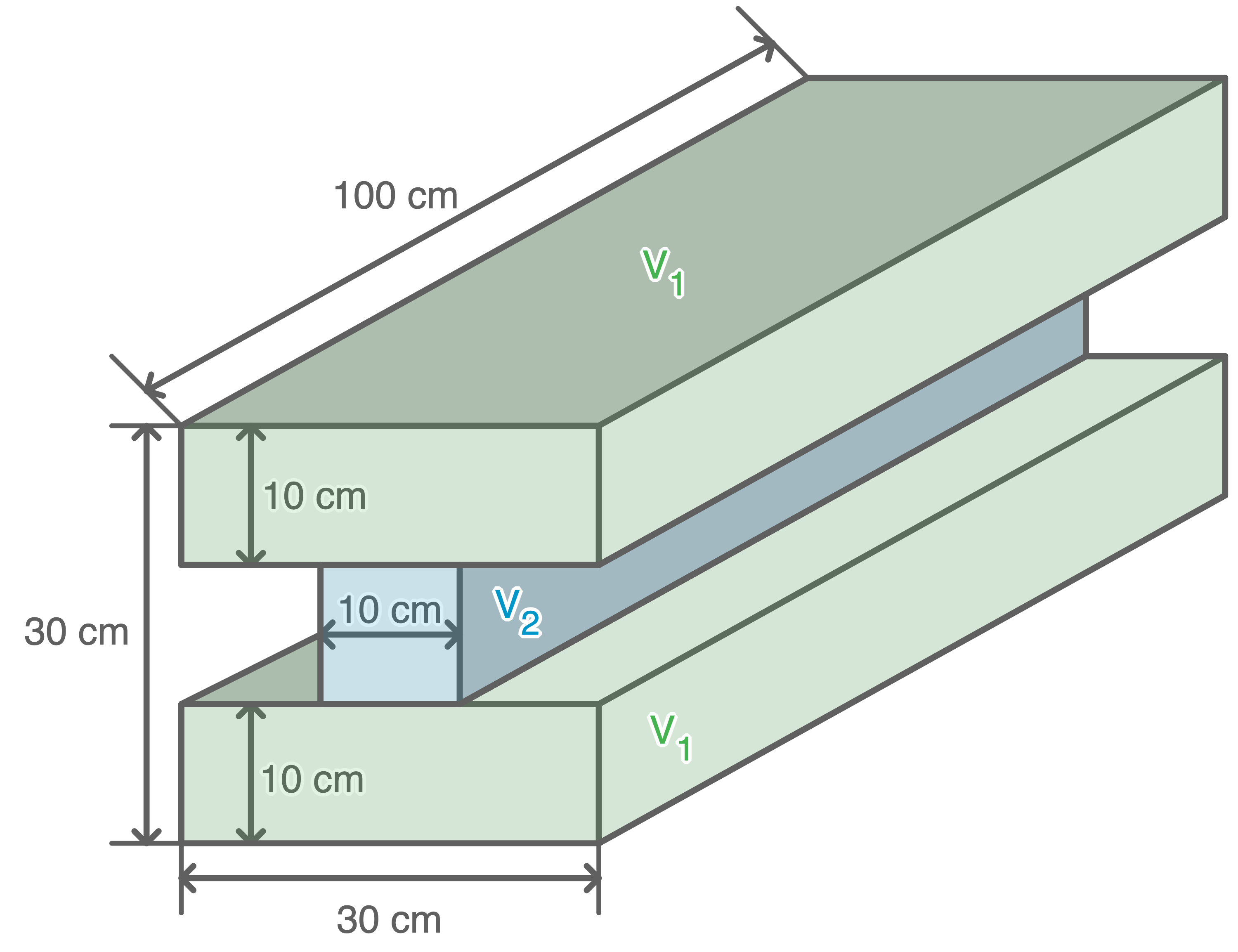
Berechne das Volumen des Körpers.
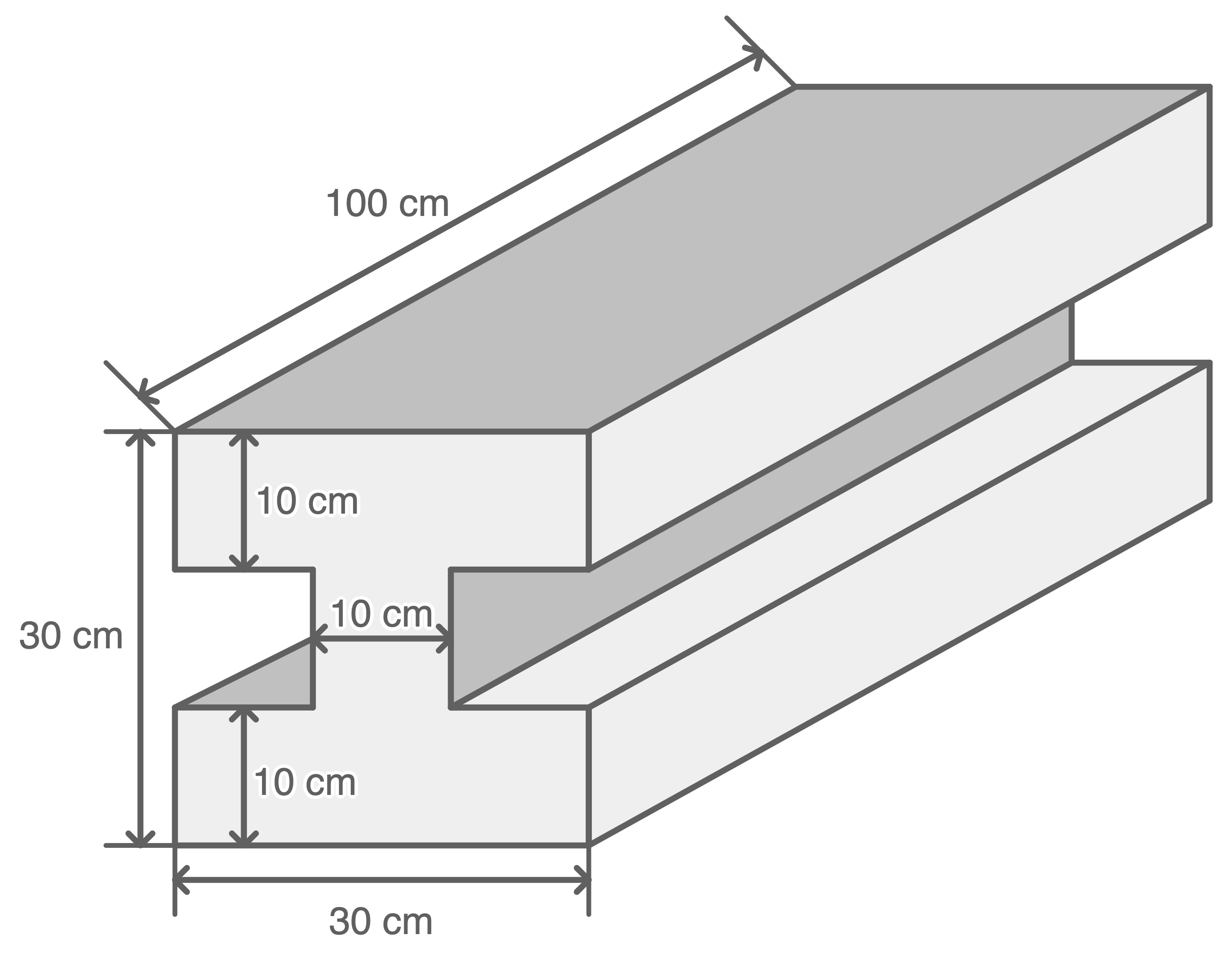

Zeichnung nicht maßstabsgetreu
(1 Pkt.)
1.
2.
Es gilt:

3.
Rechnung 1
 Rechnung 2
Rechnung 2
 Differenz
Differenz

4.
Preis für vier einzelne Kiwis:
Luisa kauft die vier Kiwis einzeln, da sie damit  spart.
spart.
| , | |||||||
| , | |||||||
| , | |||||||
| , | |||||||
| , |
5.
Oberfläche mit den vier grauen Würfeln
Ein grauer Würfel hat Flächen, die zur Oberfläche des Körpers zählen. Bei vier grauen Würfeln sind es insgeamt
Flächen, die zur Oberfläche des Körpers zählen. Bei vier grauen Würfeln sind es insgeamt  Flächen, die zur Oberfläche des Körpers zählen.
Oberfläche ohne die vier grauen Würfel
Flächen, die zur Oberfläche des Körpers zählen.
Oberfläche ohne die vier grauen Würfel
Sobald ein grauer Würfel wegfällt, fallen zwar Flächen weg, aber gleichzeitig kommen
Flächen weg, aber gleichzeitig kommen  Flächen der anderen Würfel hinzu. Bei vier grauen Würfeln sind es insgeamt
Flächen der anderen Würfel hinzu. Bei vier grauen Würfeln sind es insgeamt  Flächen, die bei der neuen Oberfläche des Körpers wegfallen.
Um wie viel
Flächen, die bei der neuen Oberfläche des Körpers wegfallen.
Um wie viel  verändert sich nun die Oberfläche des Körpers?
verändert sich nun die Oberfläche des Körpers?
![\(\begin{array}[t]{rll}
O_{\text{Veränderung}}&=&16\cdot a^2-8\cdot a^2 \\[5pt]
O_{\text{Veränderung}}&=&16\cdot (1\,\text{cm})^2-8\cdot (1\,\text{cm})^2 \\[5pt]
O_{\text{Veränderung}}&=&16\,\text{cm}^2-8\,\text{cm}^2 \\[5pt]
O_{\text{Veränderung}}&=&8\,\text{cm}^2 \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/acbedc79c0a71a919bc7feb9c6136e88c4046bd359471e88ff1502665e8e0205_light.svg) Die Oberfläche wird also um
Die Oberfläche wird also um  kleiner.
kleiner.
Ein grauer Würfel hat
Sobald ein grauer Würfel wegfällt, fallen zwar
6.
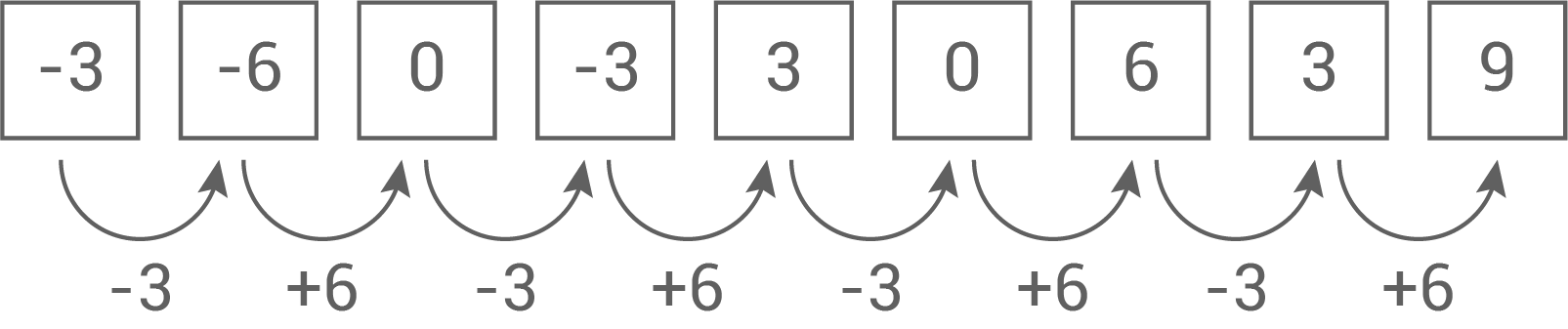
7.
8.
Um anzugeben, wie viel Prozent der Wähler Partei C gewählt haben, wird der Mittelpunktswinkel des Segments „Partei C“ benötigt:
Durch Messung mit dem Geodreieck ergeben sich  Dreisatz anwenden:
Dreisatz anwenden:




![\(\begin{array}{rcl}
100\,\% & \mathrel{\widehat{=}}& 360^{\circ}\\[5pt]
10\,\% & \mathrel{\widehat{=}}& 36^{\circ}\\[5pt]
20\,\% & \mathrel{\widehat{=}}& 72^{\circ}\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/e8f8677a73dbf46fac906b0a62ea270e5e40aabe2b5f8bec081183224bb9a2a1_light.svg)




 Prozent der Wähler haben Partei C gewählt.
Prozent der Wähler haben Partei C gewählt.
9.
Konstruktionsschritte:
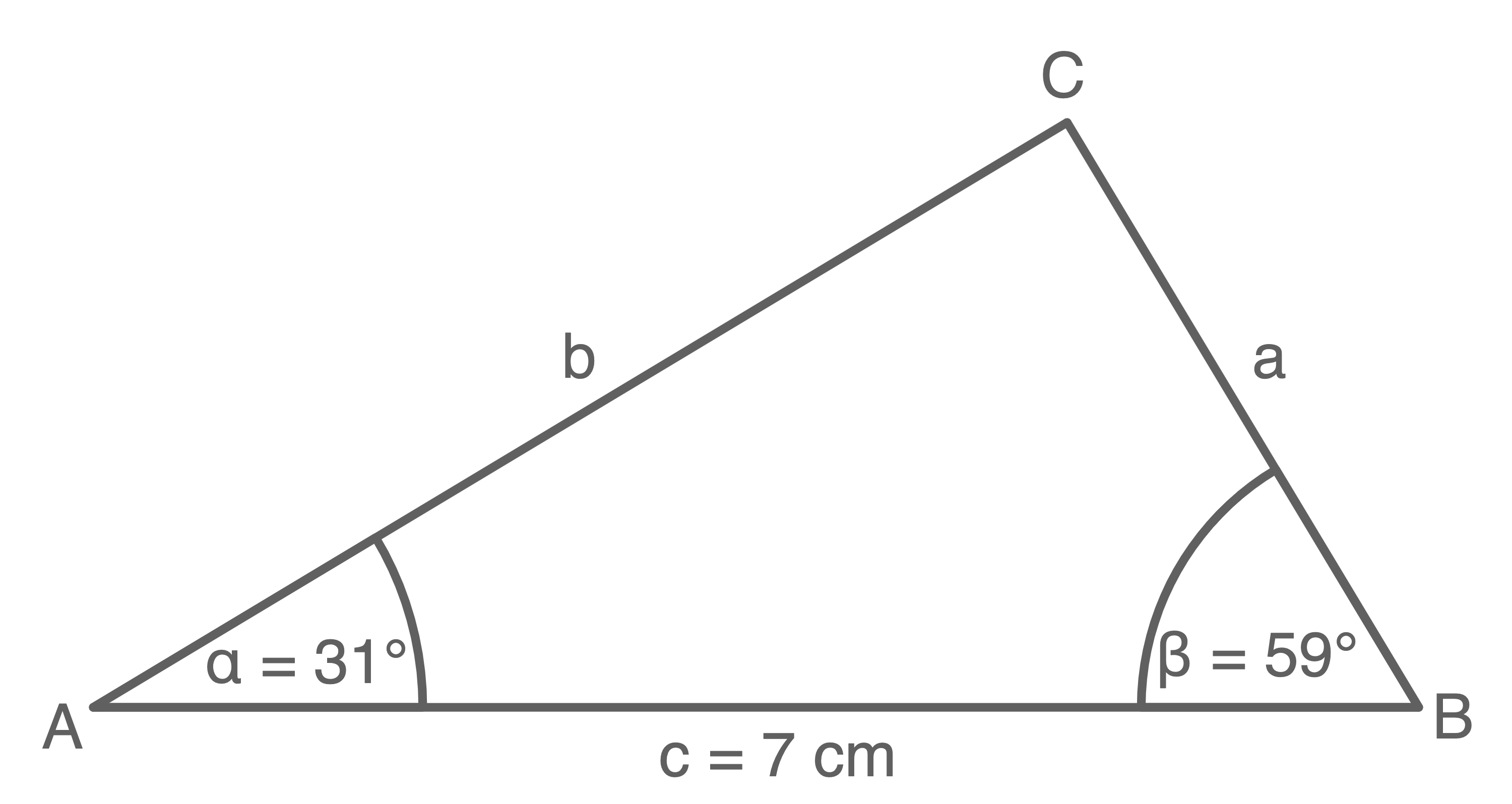
- Seite
zeichnen.
- Winkel
in Punkt A abtragen und Seite
mit beliebiger Länge einzeichnen.
- Winkel
in Punkt B abtragen und Seite
mit beliebiger Länge einzeichnen.
- Der Schnittpunkt der Seiten
und
bildet den Punkt

10.
Um das Volumen zu berechnen, wird der Körper in berechenbare Teilkörper zerlegt.
Eine mögliche Zerlegung:
 Volumen
Volumen  berechnen
berechnen
![\(\begin{array}[t]{rll}
V_1&=&a\cdot b\cdot c\\[5pt]
V_1&=&30\,\text{cm} \cdot 10\,\text{cm} \cdot 100\,\text{cm} \\[5pt]
V_1&=&30\,000\,\text{cm}^3
\end{array}\)](https://www.schullv.de/resources/formulas/d58508f602292dbc71359d0266202ccb41a2eb1135ce524d0330f803e4dc9d16_light.svg) Volumen
Volumen  berechnen
berechnen
![\(\begin{array}[t]{rll}
V_2&=&a\cdot b\cdot c\\[5pt]
V_2&=&10\,\text{cm} \cdot 10\,\text{cm} \cdot 100\,\text{cm} \\[5pt]
V_2&=&10\,000\,\text{cm}^3
\end{array}\)](https://www.schullv.de/resources/formulas/9048a52d9f5bde92eab71d8adc2a85d8ba565c759aede1e06b24d6c8da6d677a_light.svg) Volumen des gesamten Körpers berechnen
Volumen des gesamten Körpers berechnen
![\(\begin{array}[t]{rll}
V_{\text{Körper}}&=& 2\cdot V_1+V_2 \\[5pt]
V_{\text{Körper}}&=& 2\cdot 30\,000\,\text{cm}^3+10\,000\,\text{cm}^3 \\[5pt]
V_{\text{Körper}}&=& 70\,000\,\text{cm}^3 \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/bc0d132b8ee747774997dbc788f064105602011e6ec66a2cedf321dbfb59581a_light.svg)
