Wahlpflichtaufgaben
Aufgabe 1 – Kaffee
a)
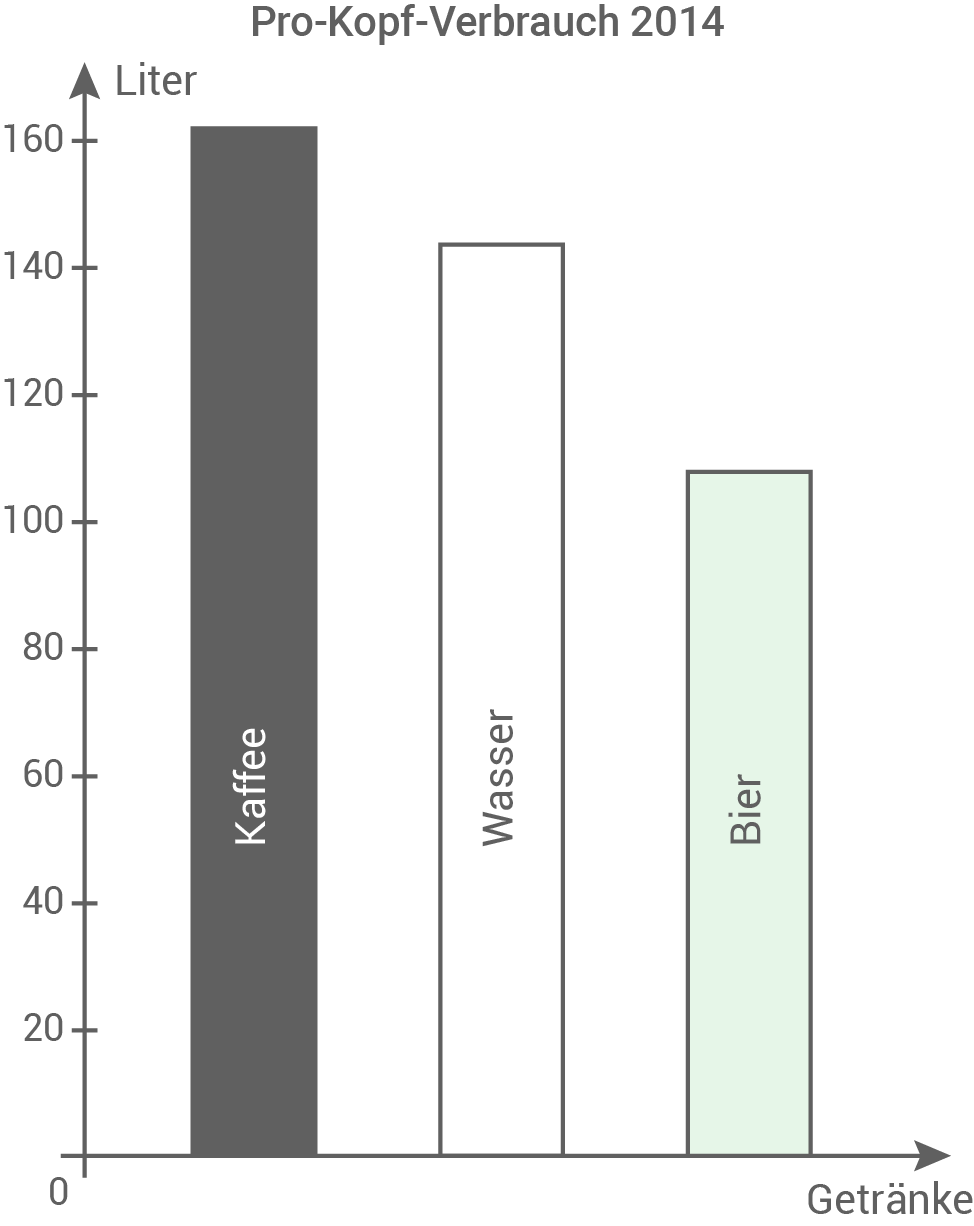
Die Werte zeigen den durchschnittlichen Pro-Kopf-Verbrauch in Deutschland im Jahr 2014:
- Kaffee:
- Wasser:
- Bier:
(2 Pkt.)
b)
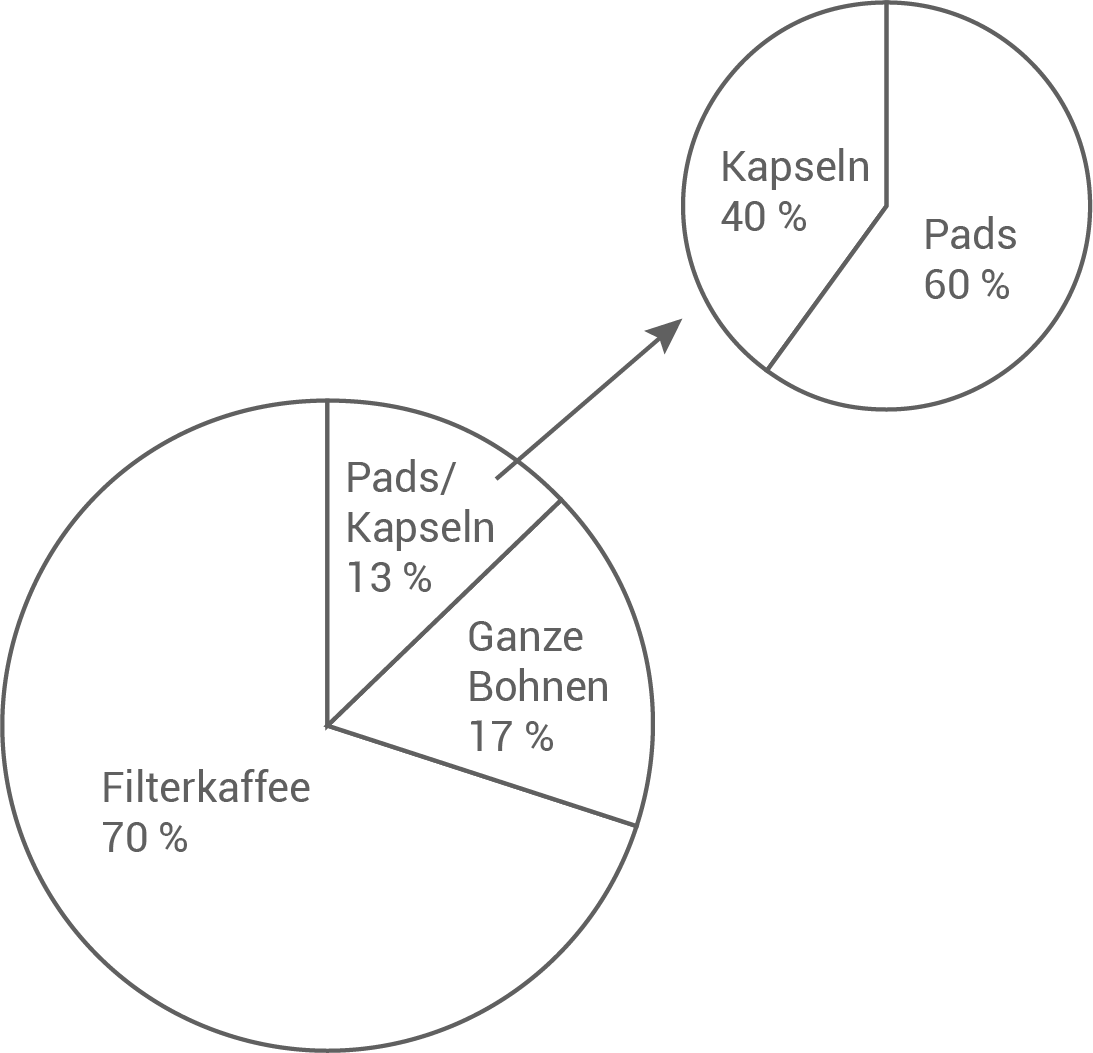
Wie viel Liter Kaffee werden mit Kapseln zubereitet?
Kaffeekonsum in Deutschland
162 Liter
162 Liter

(2 Pkt.)
c)
Die Abbildung zeigt eine Verpackung, in der sich 16 Kaffeepads befinden.
16 Kaffeepads haben ein Volumen von
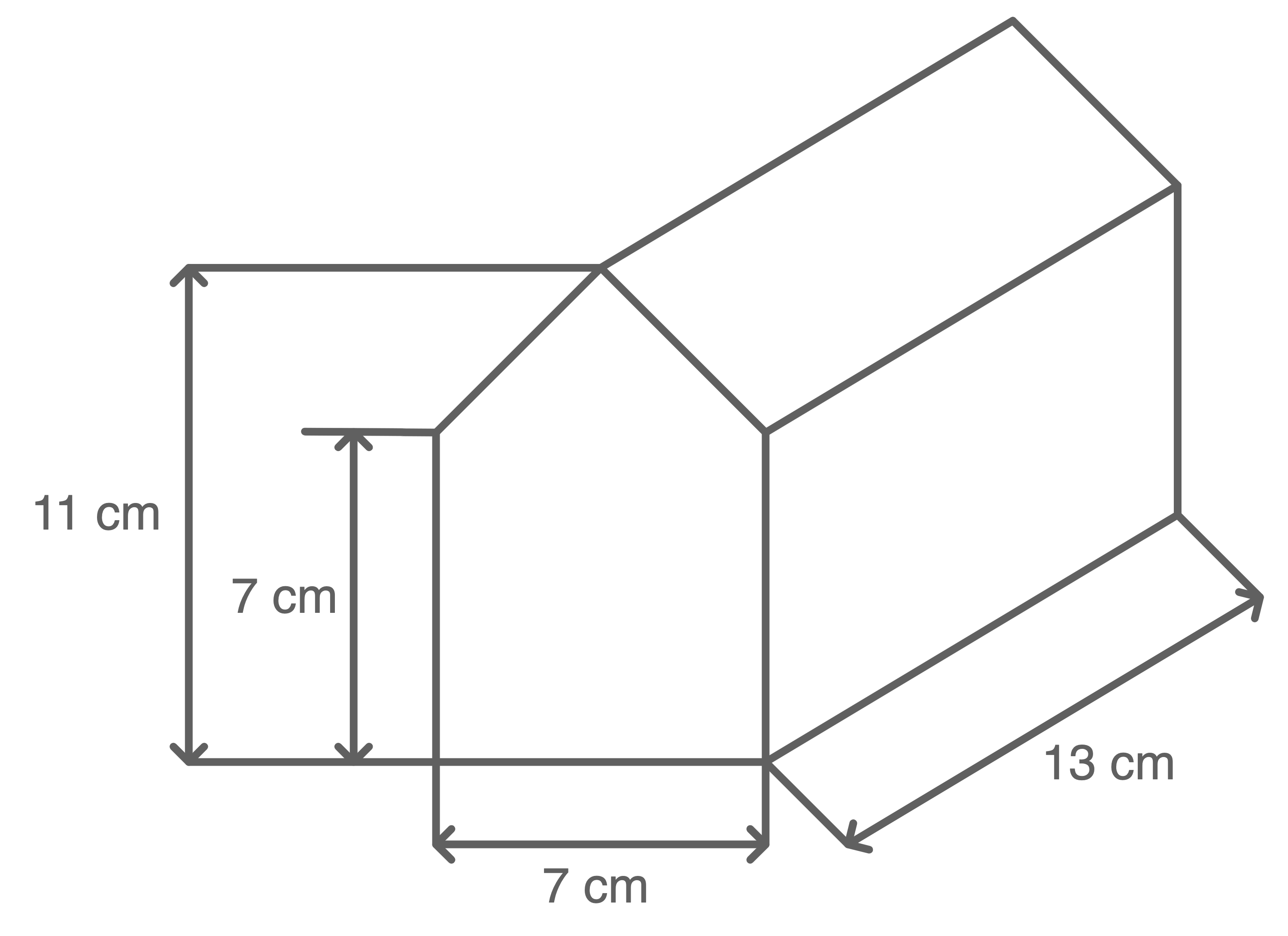
16 Kaffeepads haben ein Volumen von

Mogelpackung
Eine Verpackung muss mindestens zu befüllt sein, ansonsten gilt sie als Mogelpackung.
befüllt sein, ansonsten gilt sie als Mogelpackung.
Handelt es sich hierbei um eine Mogelpackung? Berechne und begründe deine Antwort.
Eine Verpackung muss mindestens zu
(2 Pkt.)
Aufgabe 2 – Dinosaurier
a)
Das Auto ist genau  lang.
lang.
 Ermittle möglichst genau die wirkliche Spannweite des Flugsauriers.
Ermittle möglichst genau die wirkliche Spannweite des Flugsauriers.

(2 Pkt.)
b)
Ein Argentinosaurus wog ca.  Tim sagt: „Alle 450 Schülerinnen und Schüler unserer Schule wiegen zusammen mehr.“
Tim sagt: „Alle 450 Schülerinnen und Schüler unserer Schule wiegen zusammen mehr.“
Hat er recht? Begründe rechnerisch.
Hat er recht? Begründe rechnerisch.
(2 Pkt.)
c)
Die Entwicklung der Tierarten ist in Form einer Uhr dargestellt.
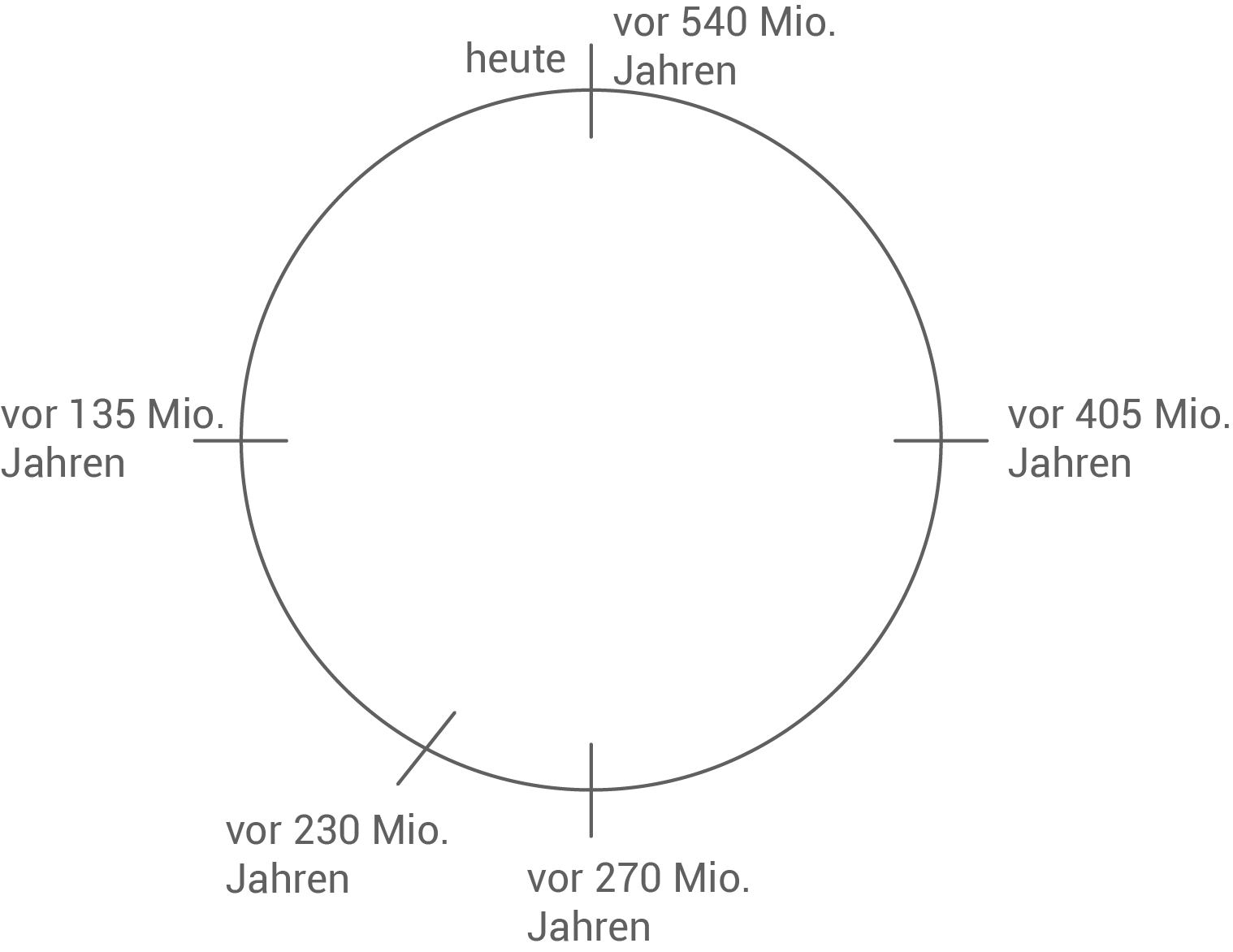 Man nimmt an, dass:
Man nimmt an, dass:
 .
.
Zeichne genau den Zeitraum ein, in dem die Dinosaurier gelebt haben.

- die Entwicklung der Tierarten vor
Jahren begann.
- es vor
Jahren die ersten Dinosaurier gab.
- die Dinosaurier vor
Jahren ausgestorben sind.
Zeichne genau den Zeitraum ein, in dem die Dinosaurier gelebt haben.
(2 Pkt.)
Aufgabe 3 – Sticker
a)
In einem Supermarkt erhält man je  Einkaufswert ein Stickerpäckchen.
Einkaufswert ein Stickerpäckchen.

- Wie viele Stickerpäkchen erhält Marie für folgenden Einkauf?
| Einkaufsliste |
|---|
| 2 Butter |
| 1 Waschmittel |
| 1 Kiste Saft |
| 3 Milch |
| 1 kg Äpfel |

- Simon fehlen bei seinem Einkauf noch Waren im Wert von mindestens
, damit er 3 Stickerpäckchen erhält.
Wie teuer ist sein bisheriger Einkauf?
(2 Pkt.)
b)
Eine Firma möchte auf dem Plakat 150 Sticker in Originalgröße abbilden.
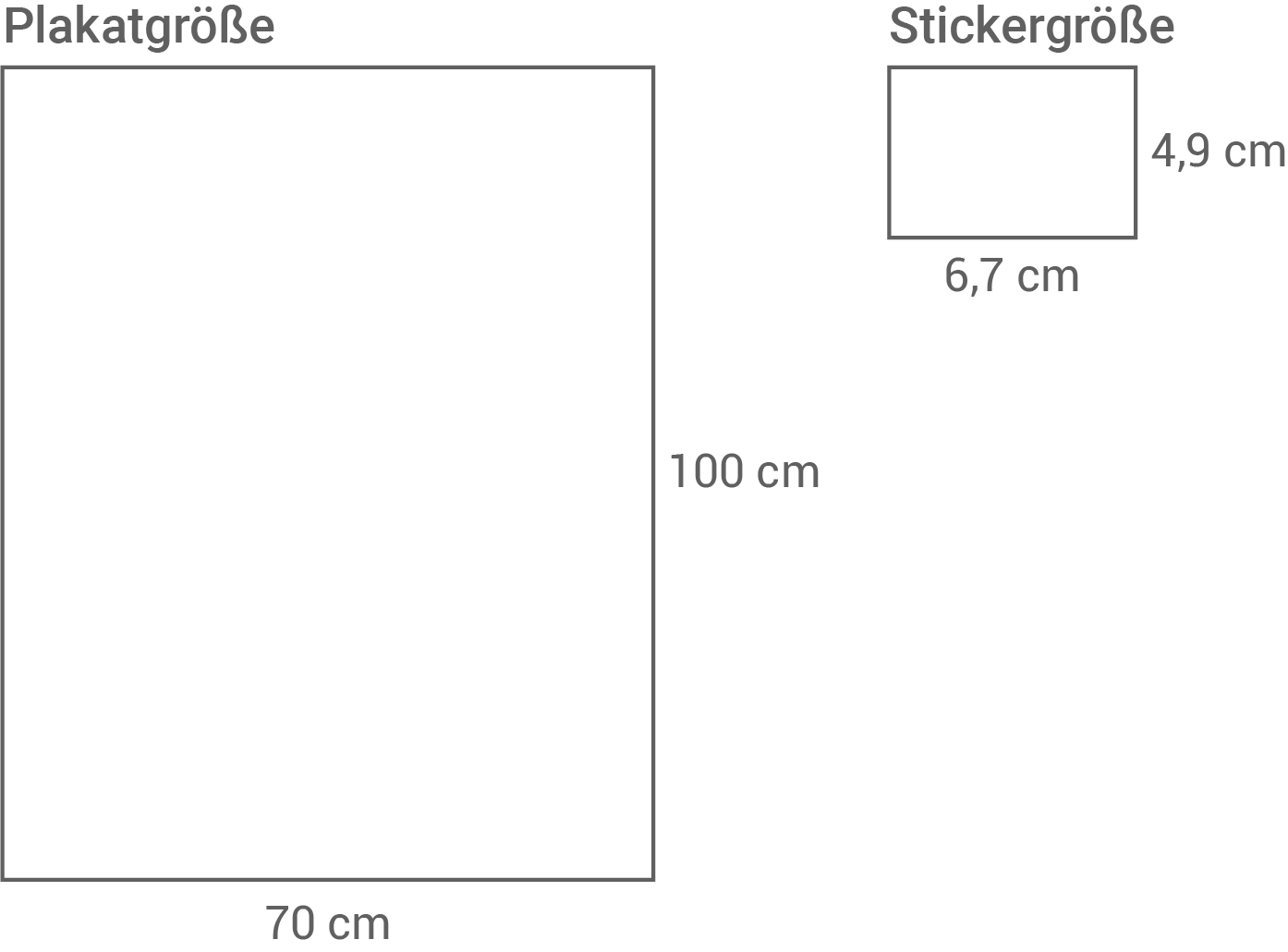 Wie viel Prozent der Fläche des Plakates sind mit Stickern bedeckt?
Wie viel Prozent der Fläche des Plakates sind mit Stickern bedeckt?

Zeichnungen nicht maßstabsgetreu
(2 Pkt.)
c)
Sascha kauft 200 Sticker in einer verschlossenen quaderförmigen Box.
Ein Sticker hat die Maße x
x  und ist
und ist  dick.
Zeichne das Netz der quaderförmigen Box.
dick.
Zeichne das Netz der quaderförmigen Box.
Ein Sticker hat die Maße
(2 Pkt.)
Aufgabe 4 – Fitnessstudio
a)
Wie oft muss Max monatlich mindestens ins Fitnessstudio gehen, damit sich für ihn ein Jahresbeitrag lohnt?
Fitnessstudio
Tageskarte: 
Jahresbeitrag:
Jahresbeitrag:
(2 Pkt.)
b)
Das Bild zeigt eine aus drei Zylindern zusammengesetzte Hantel.

 Die Hantel wird gleichmäßig mit Wasser befüllt.
Die Hantel wird gleichmäßig mit Wasser befüllt.


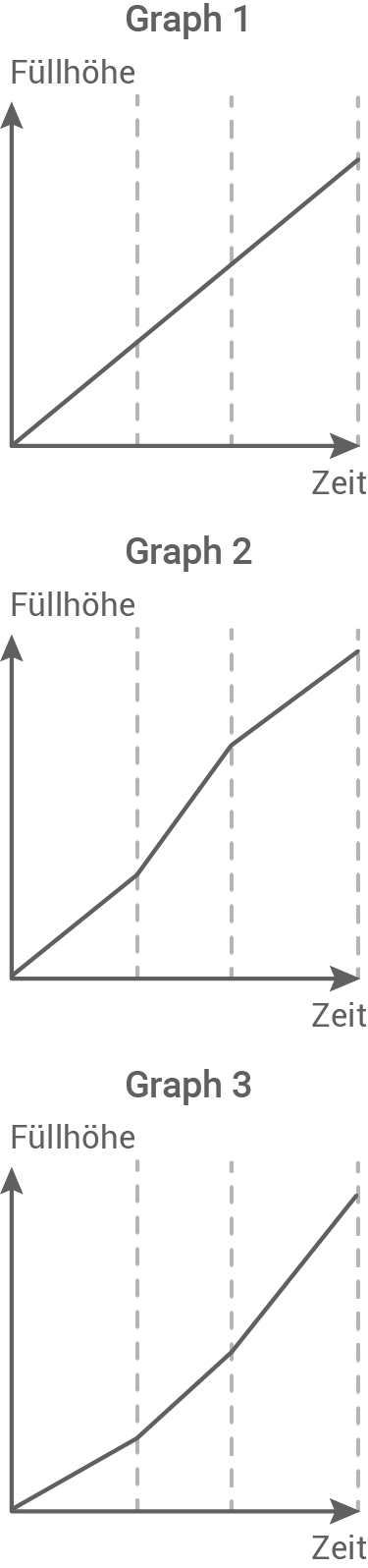
- Welcher Graph passt zu diesem Vorgang?
- Begründe, warum der von dir gewählte Graph zum Füllvorgang passt.
(2 Pkt.)
c)
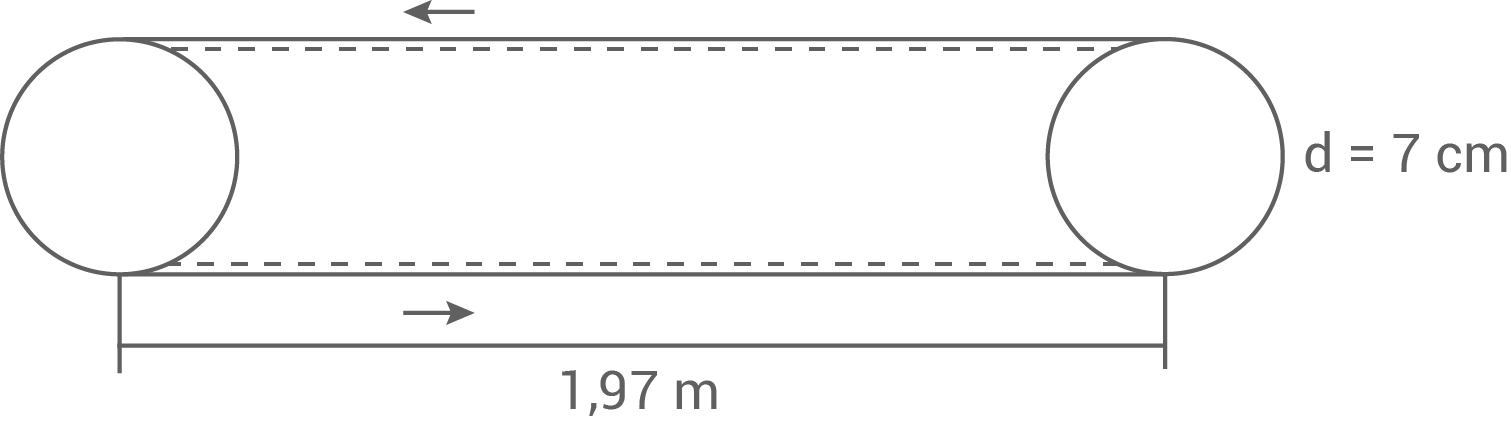
Moritz läuft 60 Minuten auf dem Laufband. Dabei dreht sich das Laufband 2650 Mal.
 Wie viel Kilometer ist Moritz gelaufen?
Wie viel Kilometer ist Moritz gelaufen?

(2 Pkt.)
Lösung 1
a)
Maßstab:  Daraus folgt:
Daraus folgt:

b)
Wie viel Liter Kaffee werden mit Pads/Kapseln zubereitet?
 Liter Kaffee werden mit Pads/Kapseln zubereitet.
Liter Kaffee werden mit Pads/Kapseln zubereitet.
Jetzt kann berechnet werden, wie viel Liter nur mit Kapseln zubereitet werden. Wie viel Liter Kaffee werden mit Kapseln zubereitet? Liter Kaffe werden mit Kapseln zubereitet.
Liter Kaffe werden mit Kapseln zubereitet.
Lösung über den Dreisatz




![\(\begin{array}{rcl}
100\,\% & \mathrel{\widehat{=}}&162\,\text{l}\\[5pt]
1\,\% & \mathrel{\widehat{=}}& 1,62\,\text{l}\\[5pt]
13\,\% & \mathrel{\widehat{=}}& 21,06\,\text{l}
\end{array}\)](https://www.schullv.de/resources/formulas/9332f2f15cd40e4206911ac75780571df23d595156d285c9ce241d4274baca2a_light.svg)




Lösung über die Formel
![\(\begin{array}[t]{rll}
P&=&\dfrac{G\cdot p}{100} \\[5pt]
P&=&\dfrac{162\,\text{l}\cdot 13}{100} \\[5pt]
P&=&21,06\,\text{l}\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/2799ad68ff687906174299aa176b9fc95aa0dd18836384b324a0314e3be190ac_light.svg)
Jetzt kann berechnet werden, wie viel Liter nur mit Kapseln zubereitet werden. Wie viel Liter Kaffee werden mit Kapseln zubereitet?
Lösung über den Dreisatz




![\(\begin{array}{rcl}
100\,\% & \mathrel{\widehat{=}}&21,06\,\text{l}\\[5pt]
1\,\% & \mathrel{\widehat{=}}& 0,2106\,\text{l}\\[5pt]
40\,\% & \mathrel{\widehat{=}}& 8,424\,\text{l}
\end{array}\)](https://www.schullv.de/resources/formulas/6ce9b692e70105a86af5974f380f72881d5461d9b73ff135be79c7933d1aaddb_light.svg)




Lösung über die Formel
![\(\begin{array}[t]{rll}
P&=&\dfrac{G\cdot p}{100} \\[5pt]
P&=&\dfrac{21,06\,\text{l}\cdot 40}{100} \\[5pt]
P&=&8,424\,\text{l}\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/e022eab53d6b191dbd9422c2328b164c6e36c0c08932fd5330fb0c3f7770bdee_light.svg)
Etwa
c)
Um die Frage zu beantworten, muss das Volumen der Verpackung berechnet werden.
Für das Volumen benötigt man die Grundfläche  und die Höhe
und die Höhe  des Körpers. Die Höhe ist bereits gegeben mit
des Körpers. Die Höhe ist bereits gegeben mit  Flächeninhalt der Grundfläche
Flächeninhalt der Grundfläche  berechnen
Die Grundfläche setzt sich aus einem Quadrat und einem Dreieck zusammen:
berechnen
Die Grundfläche setzt sich aus einem Quadrat und einem Dreieck zusammen:
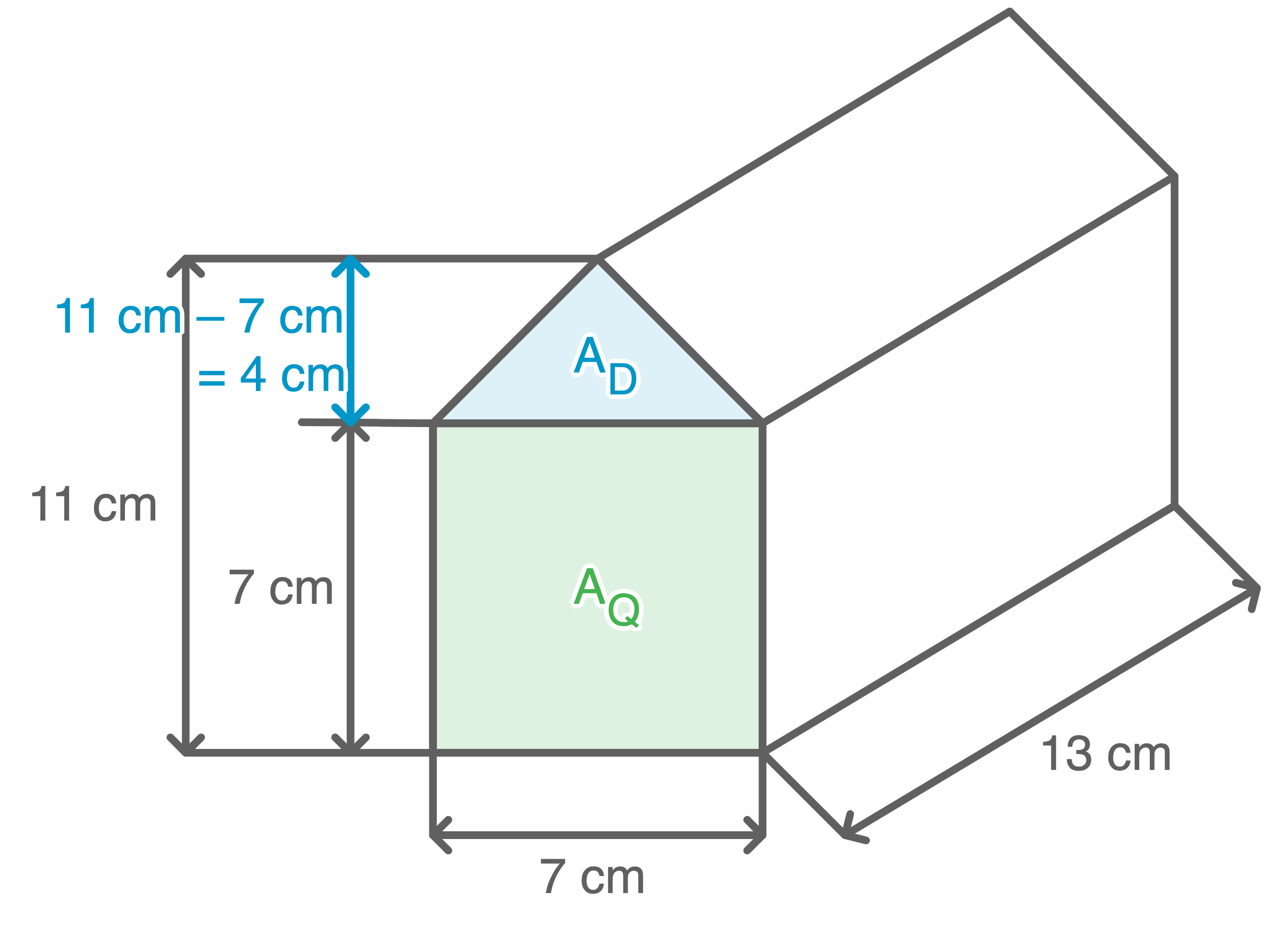 Flächeninhalt des Dreiecks berechnen
Flächeninhalt des Dreiecks berechnen
![\(\begin{array}[t]{rll}
A_D&=& \dfrac{g\cdot h}{2} \\[5pt]
A_D&=& \dfrac{7\,\text{cm}\cdot 4\,\text{cm}}{2}\\[5pt]
A_D&=&14\,\text{cm}^2\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/277cd28204cfbd676b5727e077968ab5c56d83631c7f3fa5d63db967be3c5f8e_light.svg) Flächeninhalt des Quadrats berechnen
Flächeninhalt des Quadrats berechnen
![\(\begin{array}[t]{rll}
A_Q&=& a^2 \\[5pt]
A_Q&=& (7\,\text{cm})^2 \\[5pt]
A_Q&=& 49\,\text{cm}^2 \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/22e456da299122adce1bc64965ece9423980852dc4501c3fd3168956c882fd18_light.svg) Daraus ergibt sich für
Daraus ergibt sich für  :
:
![\(\begin{array}[t]{rll}
A_{\text{gesamt}}&=&A_D+A_Q \\[5pt]
A_{\text{gesamt}}&=&14\,\text{cm}^2+49\,\text{cm}^2 \\[5pt]
A_{\text{gesamt}}&=&63\,\text{cm}^2 \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/5a9c06b2bbfa8aa9d2e7da9a16c5dae211f85c9a3b27157ffe1e6811a64ffe96_light.svg) Volumen der Verpackung berechnen
Volumen der Verpackung berechnen
![\(\begin{array}[t]{rll}
V&=&A_{\text{gesamt}}\cdot h \\[5pt]
V&=&63\,\text{cm}^2\cdot 13\,\text{cm} \\[5pt]
V&=&819\,\text{cm}^3
\end{array}\)](https://www.schullv.de/resources/formulas/86ec26aea0994d329eeaf276e379243340315b67220f8bd69b68f7bbd4e3b4c2_light.svg) 70 % des Volumens berechnen
70 % des Volumens berechnen
 Kaffee enthalten ist. Es müssten aber mindestens
Kaffee enthalten ist. Es müssten aber mindestens  enthalten sein.
enthalten sein.

Lösung über den Dreisatz




![\(\begin{array}{rcl}
100\,\% & \mathrel{\widehat{=}}&819\,\text{cm}^3\\[5pt]
1\,\% & \mathrel{\widehat{=}}&8,19\,\text{cm}^3\\[5pt]
70\,\% & \mathrel{\widehat{=}}&573,3\,\text{cm}^3\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/5606ffe2cc82d04cd18933a2b759d066fc7cf375843d96e77000cae876011344_light.svg)




Lösung über die Formel
![\(\begin{array}[t]{rll}
P&=&\dfrac{G\cdot p}{100} \\[5pt]
P&=&\dfrac{819\,\text{cm}^3\cdot 70}{100} \\[5pt]
P&=&573,3\,\text{cm}^3\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/7a93cc0aec9ec94e2cac56e073e98bc33ba0ac93a75e423c9330ac5a455246b9_light.svg)
Es handelt sich um eine Mogelpackung, da nur Lösung 2
a)
Maße des Autos in der Zeichnung: 
Maße der Spannweite in der Zeichnung: Je nach Bildschirmgröße kann die Messung variieren. Die Vorgehensweise bleibt jedoch die gleiche.
Mit diesen Angaben kann mithilfe des Dreisatzes die wirkliche Spannweite ermittelt werden:
Je nach Bildschirmgröße kann die Messung variieren. Die Vorgehensweise bleibt jedoch die gleiche.
Mit diesen Angaben kann mithilfe des Dreisatzes die wirkliche Spannweite ermittelt werden:




![\(\begin{array}{rcl}
5,1\,\text{cm} & \mathrel{\widehat{=}}& 4,3\,\text{m}\\[5pt]
1\,\text{cm} & \mathrel{\widehat{=}}& \dfrac{4,3}{5,1}\,\text{m}\\[5pt]
12,7\,\text{cm} & \mathrel{\widehat{=}}& \dfrac{4,3}{5,1} \cdot 12,7\,\text{m}\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/ed67ebc07102c12075860863889cd5d68515ccf2c45404ad017726fb3120dcb8_light.svg)




 Die wirkliche Spannweite des Flugsauriers beträgt etwa
Die wirkliche Spannweite des Flugsauriers beträgt etwa 
Maße der Spannweite in der Zeichnung:
b)
Wenn Tims Aussage stimmt, dann beträgt das durchschnittliche Gewicht eines Schülers:  Da das nicht möglich ist, hat Tim nicht recht.
Da das nicht möglich ist, hat Tim nicht recht.
c)
Um die Uhr zu zeichnen, werden die Mittelpunktswinkel benötigt:
Mittelpunktswinkel für das Segment „Zeit, in der die Dinosaurier lebten“




![\(\begin{array}{rcl}
540\,\text{Mio. Jahre} & \mathrel{\widehat{=}}& 360^{\circ} \\[5pt]
1\,\text{Mio. Jahre} & \mathrel{\widehat{=}}& \dfrac{360}{540}^{\circ} \\[5pt]
230\,\text{Mio. Jahre} & \mathrel{\widehat{=}}& \dfrac{360}{540}\cdot 230^{\circ}
\end{array}\)](https://www.schullv.de/resources/formulas/757dc027d476e497983d94bd1d4ee9a1fbb216ba2a3100397a8c3f6dcc470e0c_light.svg)




 Mittelpunktswinkel für das Segment „Zeit nach den Dinosauriern“
Mittelpunktswinkel für das Segment „Zeit nach den Dinosauriern“




![\(\begin{array}{rcl}
540\,\text{Mio. Jahre} & \mathrel{\widehat{=}}& 360^{\circ} \\[5pt]
1\,\text{Mio. Jahre} & \mathrel{\widehat{=}}& \dfrac{360}{540}^{\circ} \\[5pt]
65\,\text{Mio. Jahre} & \mathrel{\widehat{=}}& \dfrac{360}{540}\cdot 65^{\circ}
\end{array}\)](https://www.schullv.de/resources/formulas/8851b8c0dddc191c5037cc95135cba5d27a5cddf943b4ed5bc73bb903e44cf12_light.svg)




 Uhr zeichnen
Uhr zeichnen
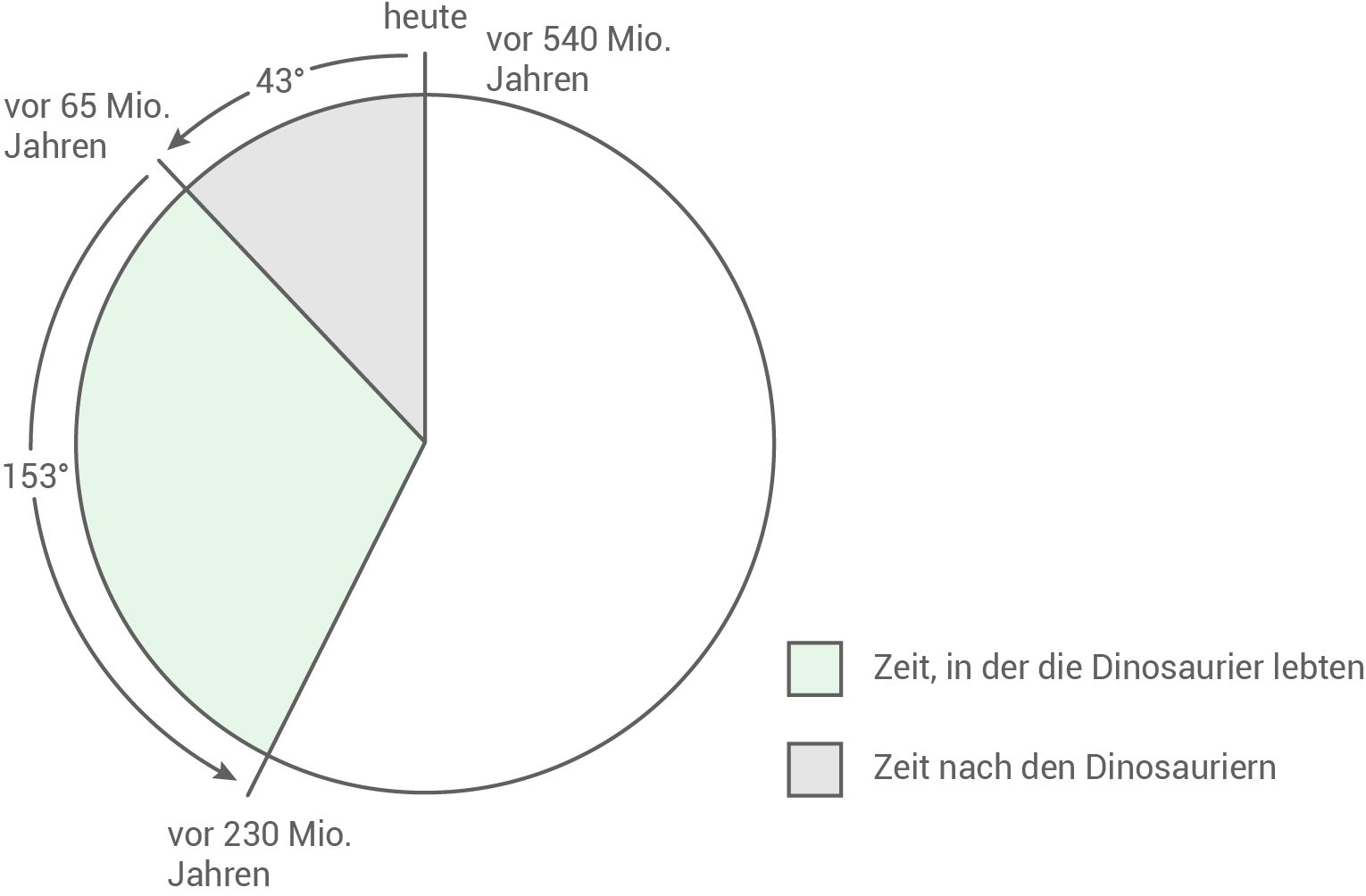 Beachte beim Zeichnen den Radius
Beachte beim Zeichnen den Radius 

Lösung 3
a)
Wie viele Stickerpäckchen erhält Marie für folgenden Einkauf?
Hierfür müssen die Gesamtkosten des Einkaufs berechnet werden:
Marie erhält 2 Stickerpäckchen für ihren Einkauf.
Wie teuer ist Simons bisheriger Einkauf?
Damit Simon 3 Stickerpäckchen bekommt, braucht er einen Einkaufswert von  Also beträgt Simons bisheriger Einkauf:
Also beträgt Simons bisheriger Einkauf: 
| , | ||||||||||
| , | ||||||||||
| , | ||||||||||
| , | ||||||||||
| , | ||||||||||
| , | ||||||||||
| , | ||||||||||
| , | ||||||||||
| , |
b)
Fläche des Plakats berechnen
![\(\begin{array}[t]{rll}
A_P&=&a\cdot b \\[5pt]
A_P&=&100\,\text{cm}\cdot 70\,\text{cm} \\[5pt]
A_P&=&7\,000\,\text{cm}^2
\end{array}\)](https://www.schullv.de/resources/formulas/b04930495497e70511bbf80916884efc6d3dcfa3d0e0cc001ee2c46873747deb_light.svg) Fläche eines Stickers berechnen
Fläche eines Stickers berechnen
![\(\begin{array}[t]{rll}
A_S&=&a\cdot b \\[5pt]
A_S&=&4,9\,\text{cm}\cdot 6,7\,\text{cm} \\[5pt]
A_S&=&32,83\,\text{cm}^2
\end{array}\)](https://www.schullv.de/resources/formulas/5e941ebdb33744d8aad7fa3003cbd421adf83d91bc3f9cb767e8001ae31a81a9_light.svg) Fläche aller Sticker berechnen
Fläche aller Sticker berechnen
![\(\begin{array}[t]{rll}
A_\text{Gesamt}&=&150\cdot A_S \\[5pt]
A_\text{Gesamt}&=&150\cdot 32,83\,\text{cm}^2 \\[5pt]
A_\text{Gesamt}&=&4\,924,5\,\text{cm}^2
\end{array}\)](https://www.schullv.de/resources/formulas/d4e0f0b63d34205c30be70762e7ed37b680fe91eef58651febb8d9bde210c900_light.svg) Prozentsatz berechnen
Lösung über den Dreisatz
Prozentsatz berechnen
Lösung über den Dreisatz
 Lösung über die Formel
Lösung über die Formel
![\(\begin{array}[t]{rll}
p\,\% &=&\dfrac{P\cdot 100}{G}\,\% & \\[5pt]
p\,\% &=&\dfrac{4\,924,5\cdot 100}{7\,000}\,\% & \\[5pt]
p\,\% &=& \boldsymbol{70,35\,\%}
\end{array}\)](https://www.schullv.de/resources/formulas/d7f9c5e7530069779b561d86652c91dbcc702e64dd55005fe63e259865069bff_light.svg) Das Plakat wäre zu
Das Plakat wäre zu  mit Stickern bedeckt.
mit Stickern bedeckt.
c)
Höhe der 200 Sticker:  Damit ergibt sich folgendes Netz:
Damit ergibt sich folgendes Netz:
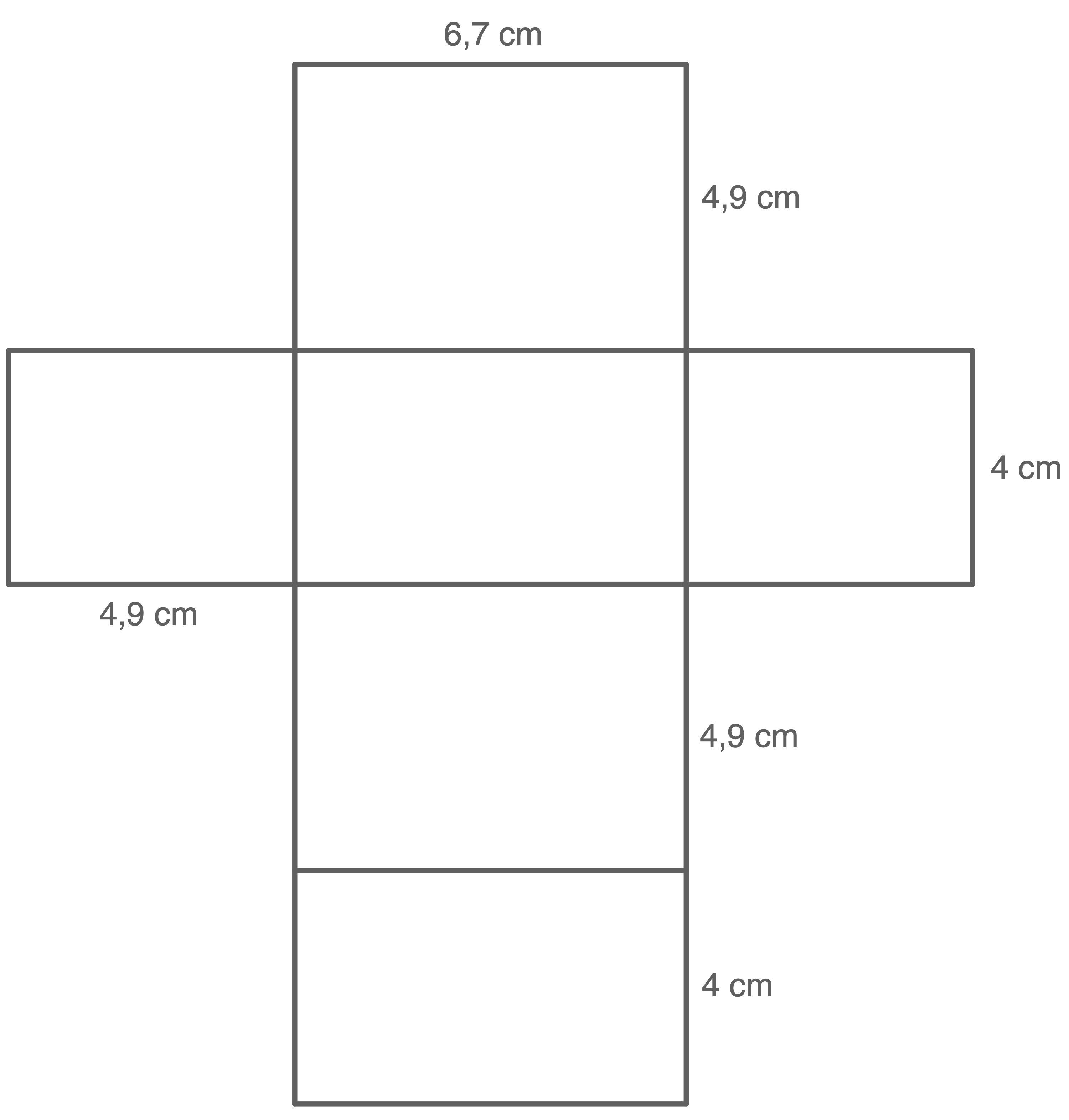

Lösung 4
a)
Der Jahresbeitrag kostet pro Monat 
 Max müsste mindestens 5-mal monatlich ins Fitnessstudio gehen, damit sich für ihn ein Jahresbeitrag lohnt.
Max müsste mindestens 5-mal monatlich ins Fitnessstudio gehen, damit sich für ihn ein Jahresbeitrag lohnt.
b)
Welcher Graph passt zu diesem Vorgang?
Graph 2
Begründung
Im ersten und letzten Abschnitt der Hantel steigt das Wasser gleich schnell. Die dazugehörigen Teilgraphen müssen dort also gleich steil verlaufen.
Im mittleren Abschnitt der Hantel steigt das Wasser schneller, da die Hantel hier schmaler ist. Der mittlere Teilgraph muss somit steiler sein.
Beides trifft auf Graph 2 zu. Bei Graph 1 steigt das Wasser bei allen Teilgraphen gleich schnell. Die Hantel müsste also in allen Abschnitten die gleiche Form haben.
Bei Graph 3 steigt das Wasser von Abschnitt zu Abschnitt immer schneller. Die Hantel müsste also von unten nach oben immer schmäler werden.
Im mittleren Abschnitt der Hantel steigt das Wasser schneller, da die Hantel hier schmaler ist. Der mittlere Teilgraph muss somit steiler sein.
Beides trifft auf Graph 2 zu. Bei Graph 1 steigt das Wasser bei allen Teilgraphen gleich schnell. Die Hantel müsste also in allen Abschnitten die gleiche Form haben.
Bei Graph 3 steigt das Wasser von Abschnitt zu Abschnitt immer schneller. Die Hantel müsste also von unten nach oben immer schmäler werden.
c)
Die Strecke, die Moritz bei einer Drehung des Laufbands zurücklegt, setzt sich zusammen aus der Länge oben, Länge unten und den beiden Halbkreisen links und rechts (= ein ganzer Kreis).
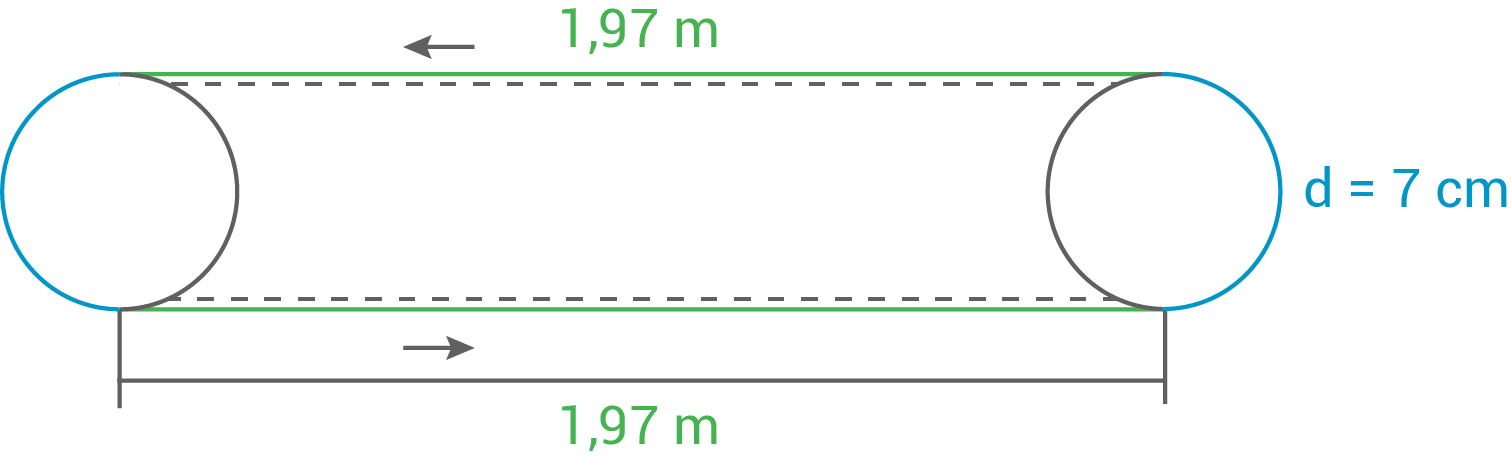 Die beiden Halbkreise entsprechen dem Umfang eines Kreises:
Die beiden Halbkreise entsprechen dem Umfang eines Kreises:
![\(\begin{array}[t]{rll}
u&=&\pi\cdot d \\[5pt]
u&=&\pi\cdot 7\,\text{cm} \\[5pt]
u&\approx&22\,\text{cm} \\[5pt]
u&=&0,22\,\text{m} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/96095db2a828a4eada688d335722263c2b8b790ed3f1c9d94aa810e97964b843_light.svg) Streckenlänge bei einer Drehung des Laufbands:
Streckenlänge bei einer Drehung des Laufbands:  Streckenlänge bei 2650 Drehungen des Laufbands:
Streckenlänge bei 2650 Drehungen des Laufbands:  Moritz ist etwa
Moritz ist etwa  gelaufen.
gelaufen.
