Pflichtteil A1

Jannik kauft ein. Wie viel muss er insgesamt bezahlen?

2 Hefte für je $89\,\text{ct}$
1 Zirkel für $9,78\,€$
1 Taschenrechner für $18,99\,€$
1 Geodreieck für $0,95\,€$

(1 Pkt.)

Trage eine passende Zahl ein.
$\dfrac{1}{4}\lt \text{____}\lt \dfrac{2}{5}$

(1 Pkt.)

Max kauft sich eine Hose und bezahlt dafür 24 Euro. Wie teuer war die Hose vorher?

Rabattaktion:
Alle Hosen sind um $70 \,\%$ reduziert!

(1 Pkt.)

Löse die Gleichung.
$35 x+16-12 x=18 x-(23+8 x)$

(1 Pkt.)

Dilara behauptet: „Alle drei Figuren haben den selben Flächeninhalt.“
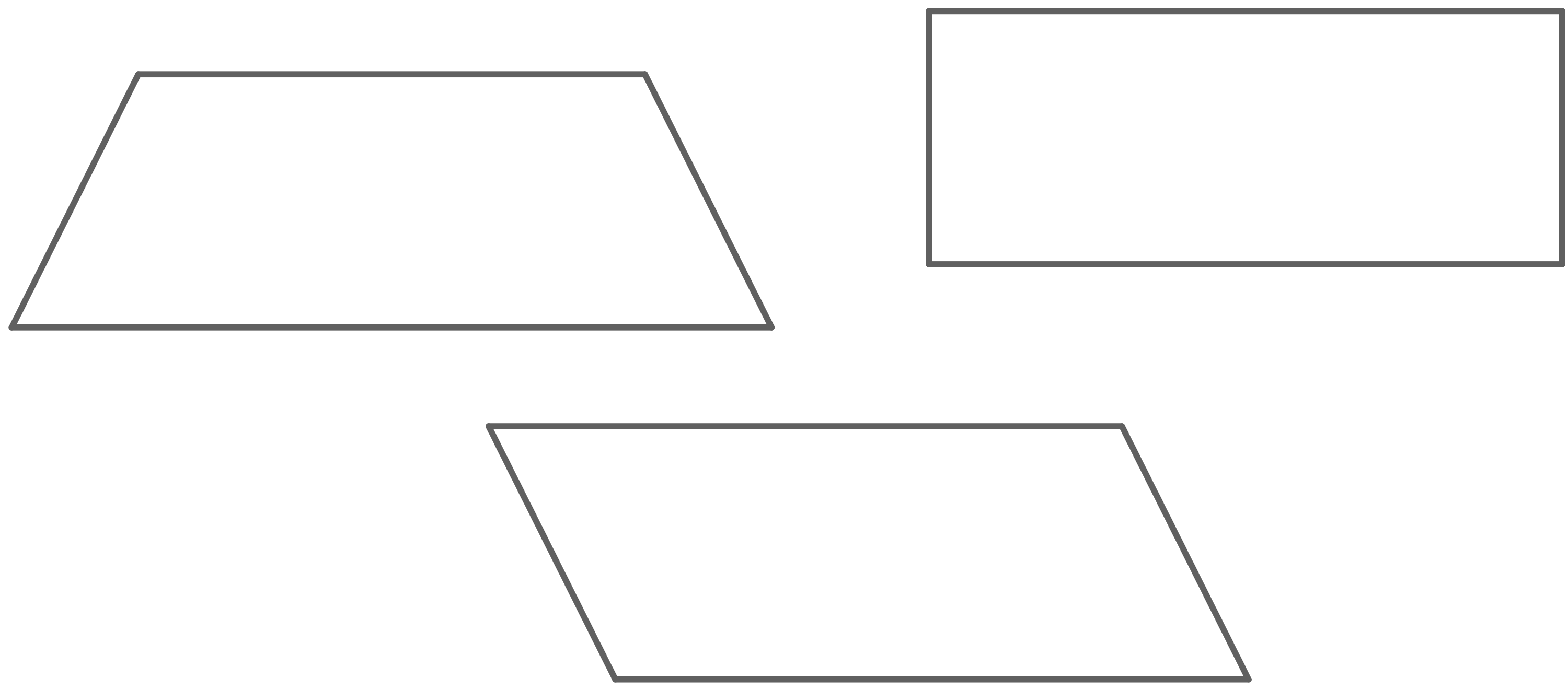
Hat sie recht? Begründe deine Antwort.

(1 Pkt.)

Ein Quader wird vollständig mit Würfeln gefüllt.
Das Volumen eines Würfels beträgt $1\,\text{dm}^3$ .

Zeichnung nicht maßstabsgetreu!

Maße des Quaders:
Länge: $2\,\text{m}$
Breite: $1\,\text{m}$
Höhe: $1,5\,\text{m}$

Wie viele $1\,\text{dm}^3$ Würfel werden benötigt?

(1 Pkt.)

Kreuze die passende Lösung an.
Jedes Rechteck ist ...

	... ein Drache
	... eine Raute
	... ein Parallelogramm
	... ein Quadrat

(1 Pkt.)

Beantworte mit Hilfe des Schaubilds folgende Fragen:

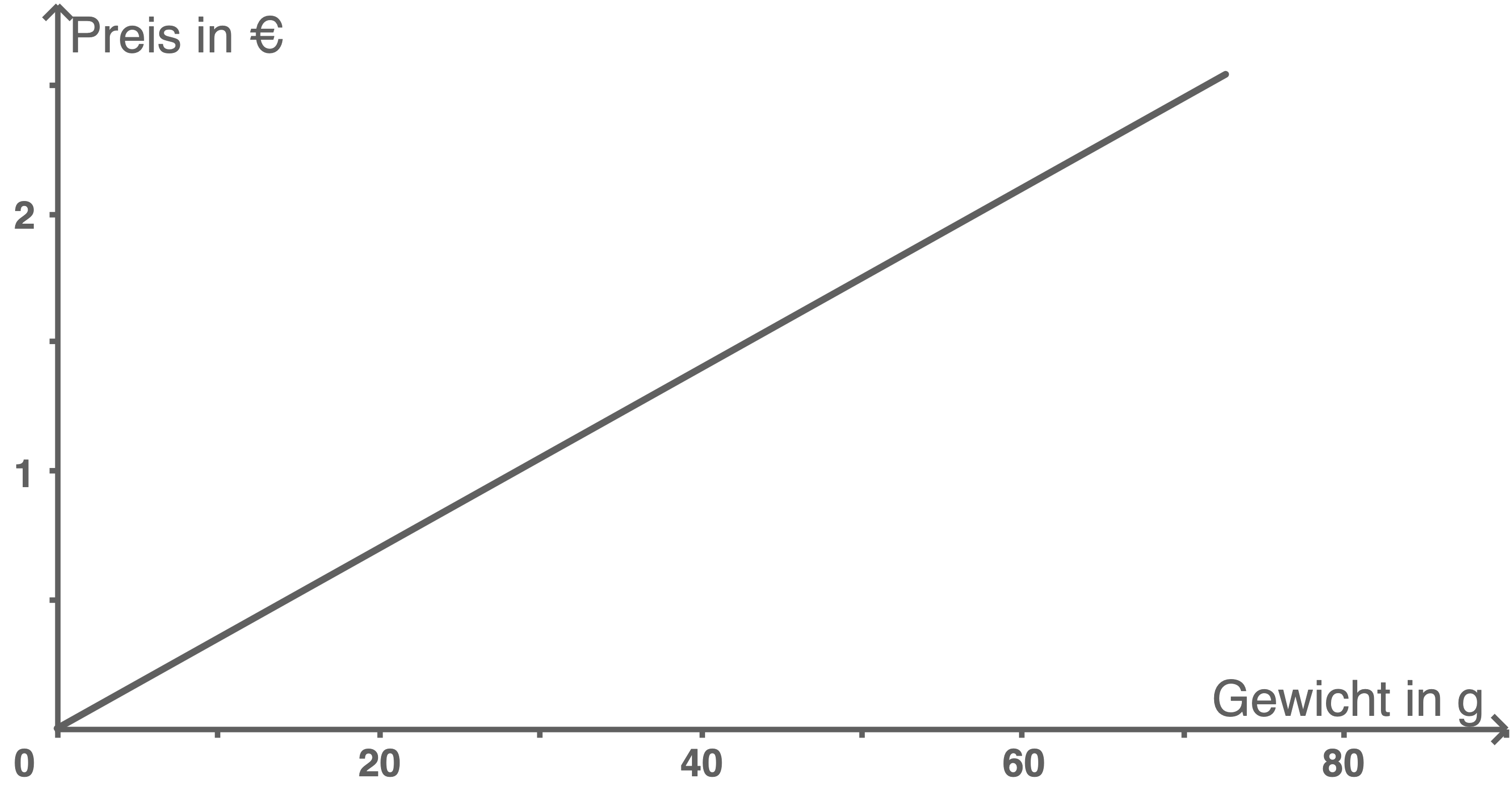
Wie viel $€$ kosten $50\,\text{g}$ Lachs?
Wie viel Lachs bekommt man für $2\,€$ ?

(1 Pkt.)

Bei diesem besonderen Würfelnetz sind drei Flächen nicht beschriftet.

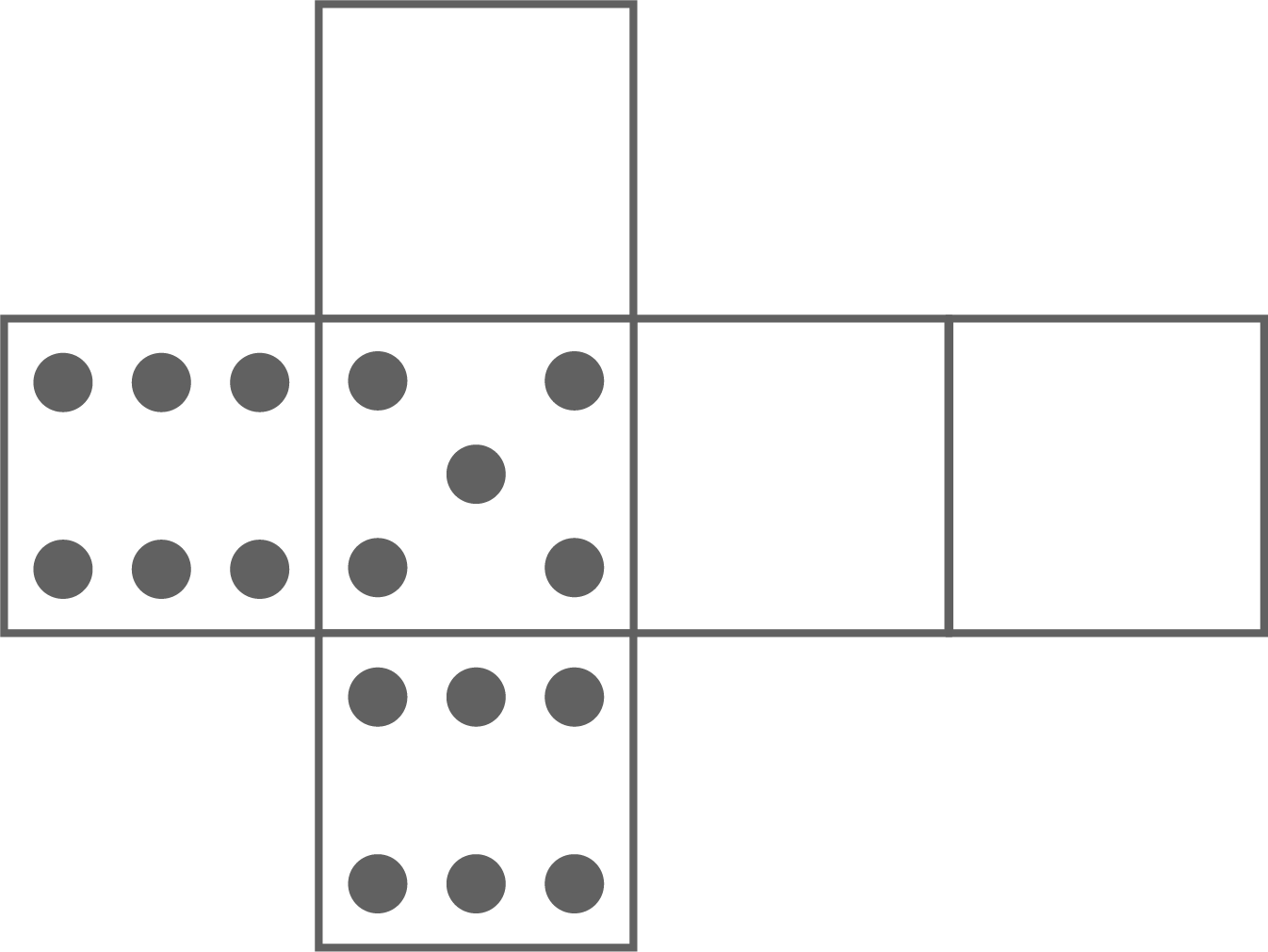Ergänze die fehlenden Augenzahlen so, dass die Wahrscheinlichkeit eine gerade Zahl zu würfeln bei $\frac{2}{3}$ liegt.
Beschrifte alle Flächen.

(1 Pkt.)

10.

Im Schülercafé wurde eine Woche lang Eis verkauft.
Die Tabelle zeigt, wie viele Eiskugeln pro Tag verkauft wurden.

Montag	45
Dienstag	103
Mittwoch	83
Donnerstag	65
Freitag	24

Wie viele Eiskugeln wurden durchschnittlich pro Tag verkauft?

(1 Pkt.)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

		$0$	,	$8$	$9$
		$0$	,	$8$	$9$
		$9$	,	$7$	$8$
	$1$	$8$	,	$9$	$9$
$+$		$0$	,	$9$	$5$

		$3$	$1$	,	$5$	$0$

Jannik muss insgesamt $31,50\,€$ bezahlen.

Hauptnenner bestimmen

$\dfrac{5}{20}\lt \text{____} \lt \dfrac{8}{20}$

Mögliche Lösungen

$\dfrac{1}{4}\lt \dfrac{6}{20}\lt \dfrac{2}{5}$ oder $\dfrac{1}{4}\lt \dfrac{7}{20}\lt \dfrac{2}{5}$

$24\,€$ entsprechen $30\,\%$ des ursprünglichen Preises, da die Hose um $70\,\%$ reduziert wurde.

$:3$

$\cdot 10$ Grau geschwungener Pfeil, der nach rechts unten zeigt.

$\begin{array}{rcl} 30\,\% & \mathrel{\widehat{=}}& 24\,€\\[5pt] 10\,\% & \mathrel{\widehat{=}}& 8\,€\\[5pt] 100\,\% & \mathrel{\widehat{=}}& 80\,€ \end{array}$

$:3$

$\cdot 10$

Die Hose hat ursprünglich $80\,€$ gekostet.

$\begin{array}[t]{rll} 35x+16-12x&=&18x-(23+8x) &\\[5pt] 35x+16-12x&=&18x-23-8x &\\[5pt] 23x+16&=&10x-23 &\quad \scriptsize \mid\;-10x \\[5pt] 13x+16&=&-23 &\quad \scriptsize \mid\;-16 \\[5pt] 13x&=&-39 &\quad \scriptsize \mid\;:13 \\[5pt] x&=&-3 \\[5pt] \end{array}$

Bei den Figuren handelt es sich um ein Rechteck, ein Trapez und ein Parallelogramm. Durch Abmessen erkennt man, dass alle drei Figuren dieselbe Höhe haben.

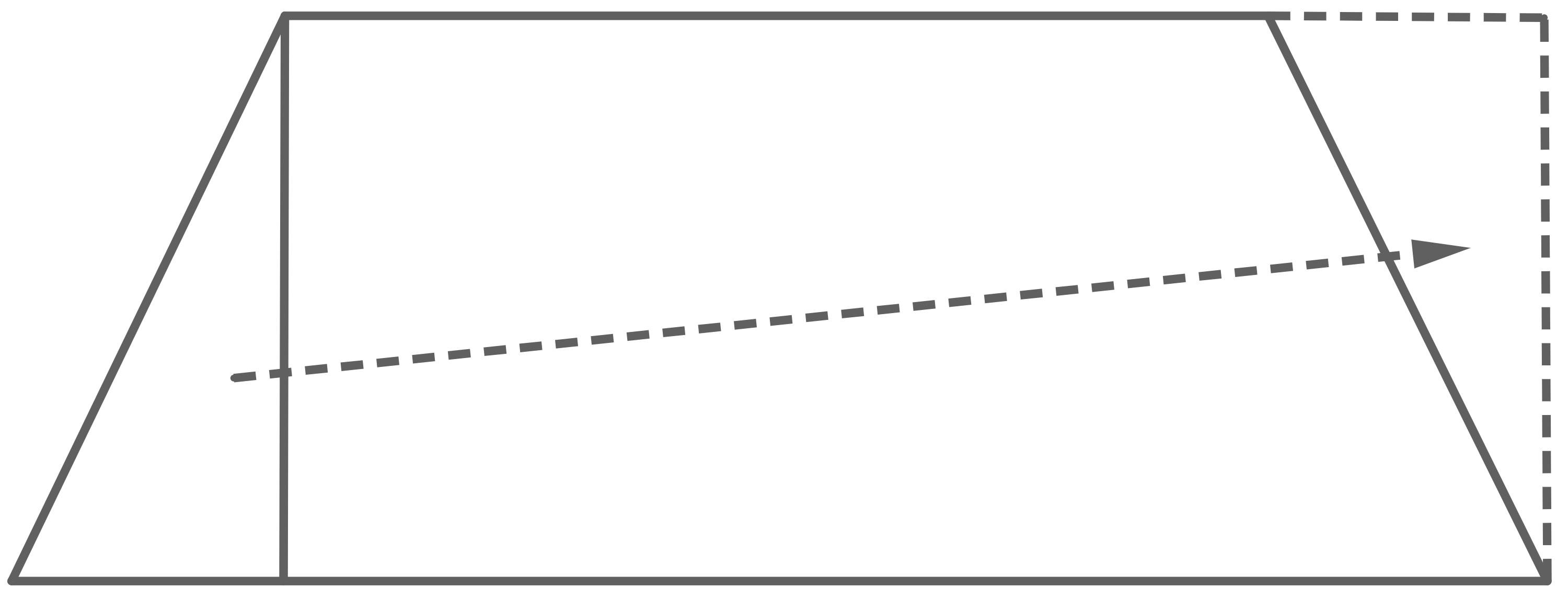
Vergleich: Rechteck und Trapez

Zerlegt man das Trapez wie abgebildet, entsteht genau die Form des Rechtecks. Somit haben die beiden Figuren denselben Flächeninhalt.

BaWü HSA 2022 Trapez Strecke Fläche Figur

Vergleich: Rechteck und Parallelogramm

Durch Abmessen erkennt man, dass diese Figuren nicht nur dieselbe Höhe, sondern auch die gleiche Grundseite haben.
Um den Flächeninhalt eines Rechtecks zu bestimmen, wird gerechnet: „Grundseite mal Höhe“
Und um den Flächeninhalt eines Parallelogramms zu bestimmen, wird ebenfalls gerechnet: „Grundseite mal Höhe“. Somit haben die beiden Figuren denselben Flächeninhalt.

Dilara hat also recht.

Alternativ können alle benötigten Seitenlängen abgemessen und der Flächeninhalt der drei Figuren berechnet werden.

1. Schritt: Volumen des Quaders berechnen

$\begin{array}[t]{rll} V&=&a\cdot b\cdot c \\[5pt] V&=&2\,\text{m}\cdot 1\,\text{m}\cdot 1,5\,\text{m} \\[5pt] V&=&2\,\text{m}^2\cdot 1,5\,\text{m} \\[5pt] V&=&3\,\text{m}^3 \end{array}$

2. Schritt: Ergebnis umrechnen in Kubikdezimeter

$3\,\text{m}^3\cdot 1\,000=3\,000\,\text{dm}^3$

3. Schritt: Anzahl der Würfel bestimmen

Da ein Würfel ein Volumen von $1\,\text{dm}^3$ und der Quader ein Volumen von $3\,000\,\text{dm}^3$ besitzt, werden $3\,000$ Würfel benötigt.

Jedes Rechteck ist ...

	... ein Drache.
	... eine Raute.
	... ein Parallelogramm.
	... ein Quadrat.

Erklärung
Eigenschaft jedes Rechtecks: Gegenüberliegende Seiten sind parallel und gleich lang.

Drache: Hat zwei Paare nebeneinanderliegender Seiten, die gleich lang sind.
Raute: Alle vier Seiten sind gleich lang.
Parallelogramm: Gegenüberliegende Seiten sind parallel und gleich lang.
Quadrat: Alle vier Seiten sind gleich lang.

$50\,\text{g}$ Lachs kosten ca. $1,75\,€$

Für $2\,€$ bekommt man ca. $58\,\text{g}$ Lachs.

Hinweis: Für die erste Lösung werden alle Ergebnisse zwischen $1,70\,€$ und $1,80\,€$ als richtig gewertet.
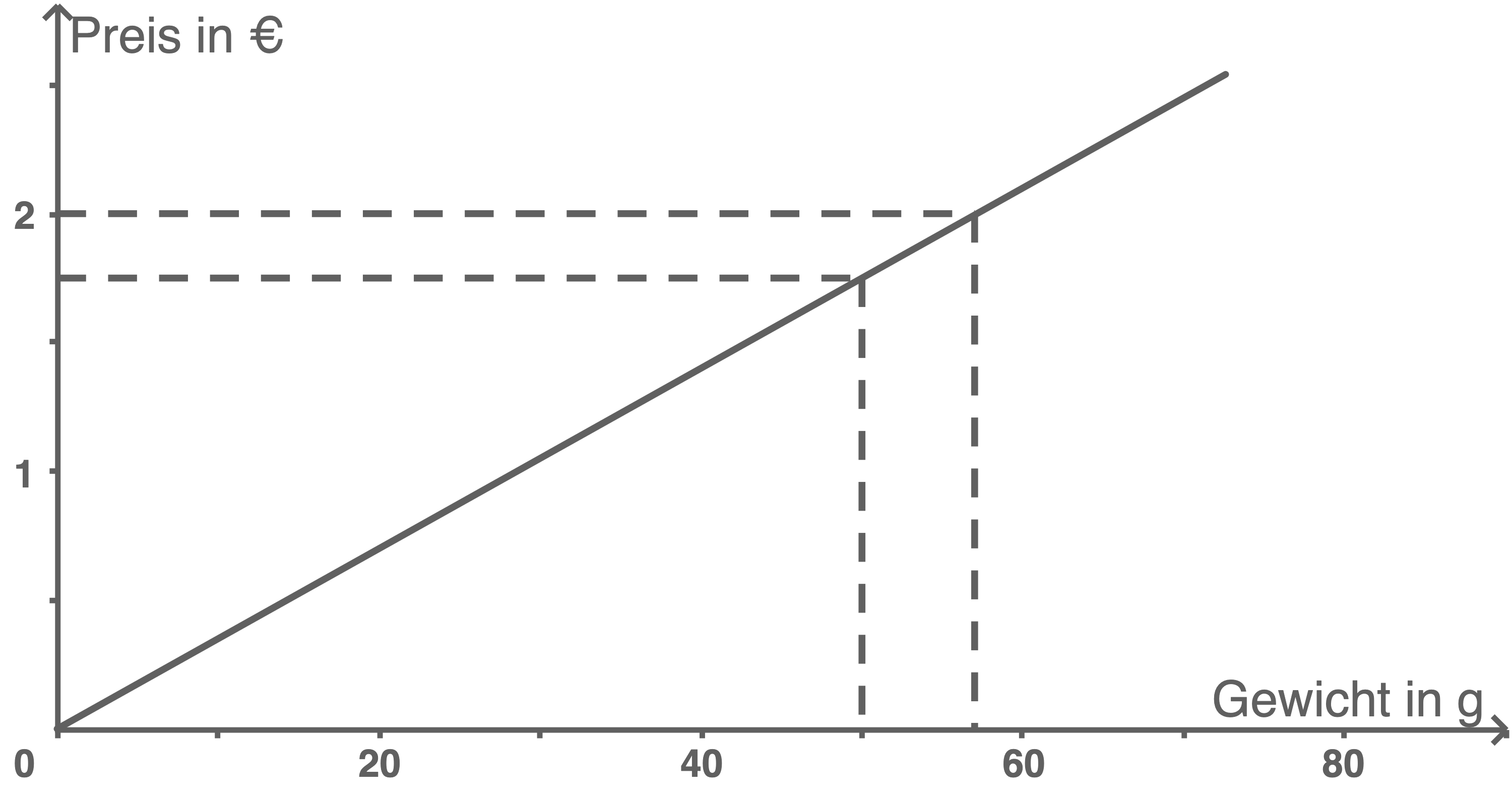
Für die zweite Lösung werden alle Ergebnisse zwischen $56\,\text{g}$ und $59\,\text{g}$ als richtig gewertet.

Um zu wissen, wie viele gerade Zahlen und wie viele ungerade Zahlen der Würfel haben muss, wird der Bruch auf den Nenner $6$ erweitert (denn der Würfel hat insgesamt 6 Flächen): $\dfrac{2}{3}=\dfrac{4}{6}.$

Der Würfel muss also

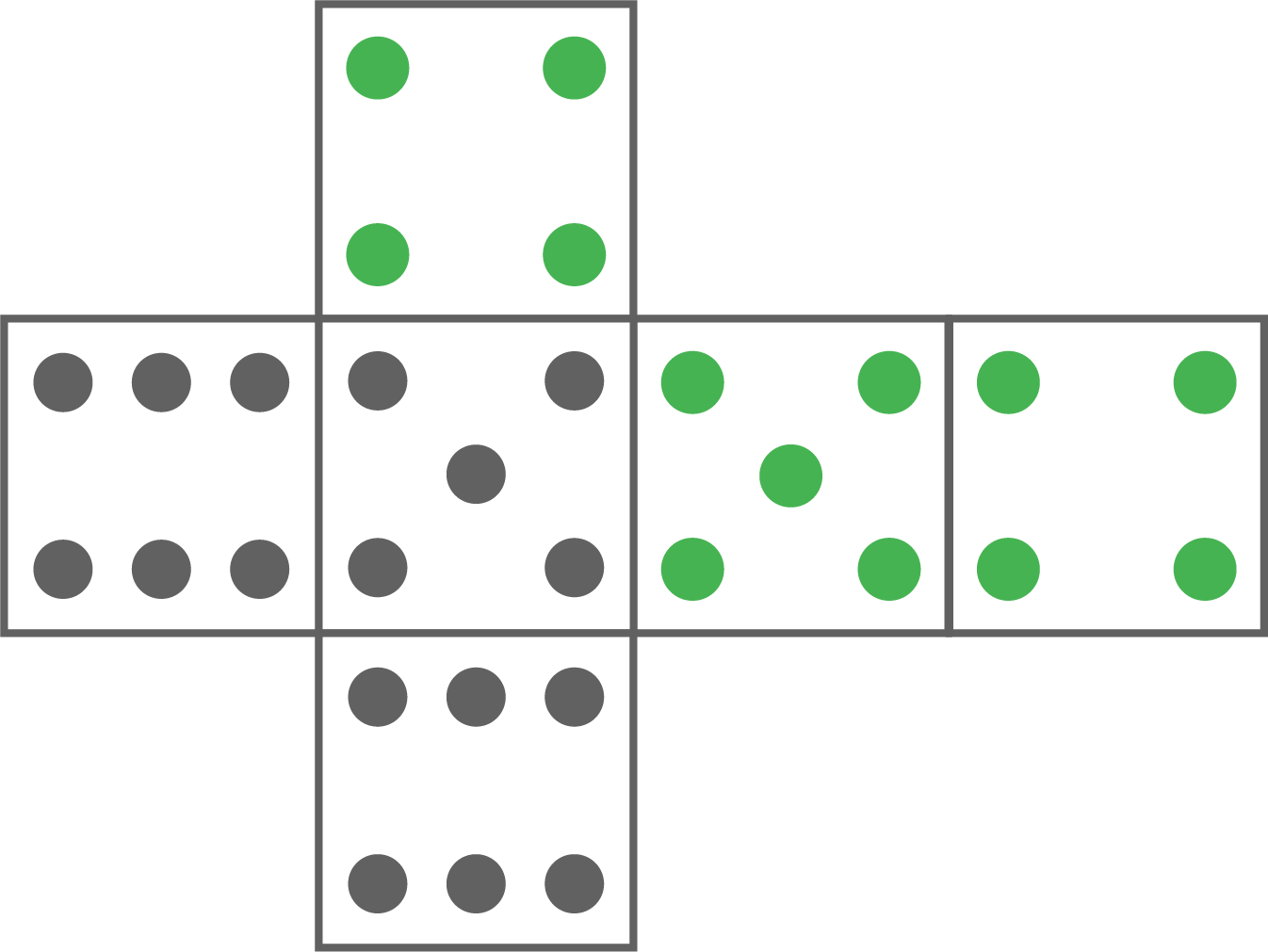
4 gerade Zahlen und
2 ungerade Zahlen besitzen

Da bereits zwei gerade Zahlen und eine ungerade Zahl eingezeichnet sind, müssen zwei weitere gerade Zahlen und eine weitere ungerade Zahl eingezeichnet werden.

Mögliche Lösung

10.

1. Schritt: Gesamtanzahl der verkauften Eiskugeln berechnen

		$4$	$5$
	$1$	$0$	$3$
		$8$	$3$
		$6$	$5$
$+$		$2$	$4$

	$3$	$2$	$0$

2. Schritt: Durchschnitt berechnen

Hier wird die Gesamtanzahl durch $5$ geteilt, da an insgesamt fünf Tagen Eis verkauft wurde.

$320:5=64$

Durchschnittlich wurden pro Tag 64 Eiskugeln verkauft.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

		$0$	,	$8$	$9$
		$0$	,	$8$	$9$
		$9$	,	$7$	$8$
	$1$	$8$	,	$9$	$9$
$+$		$0$	,	$9$	$5$

		$3$	$1$	,	$5$	$0$

		$0$	,	$8$	$9$
		$0$	,	$8$	$9$
		$9$	,	$7$	$8$
	$1$	$8$	,	$9$	$9$
$+$		$0$	,	$9$	$5$

		$3$	$1$	,	$5$	$0$

		$0$	,	$8$	$9$
		$0$	,	$8$	$9$
		$9$	,	$7$	$8$
	$1$	$8$	,	$9$	$9$
$+$		$0$	,	$9$	$5$

		$3$	$1$	,	$5$	$0$