Grundkenntnissse

Bei welchem Angebot spart man mehr Geld für das Kleidungsstück?
Begründe rechnerisch.

Angebot A

Angebot B

(1 Pkt.)

Kreuze die Aufgabe an, die das größte Ergebnis hat.

	$\dfrac{1}{2} \cdot \dfrac{1}{2}$
	$\dfrac{1}{3}-\dfrac{1}{3}-\dfrac{1}{3}$
	$\dfrac{1}{8}: \dfrac{1}{8}$
	$\dfrac{1}{5}+\dfrac{1}{5}+\dfrac{1}{5}+\dfrac{1}{5}$

(1 Pkt.)

Berechne.

$10^4 \cdot\left(8 \dfrac{1}{5}-1,7\right)$

(1 Pkt.)

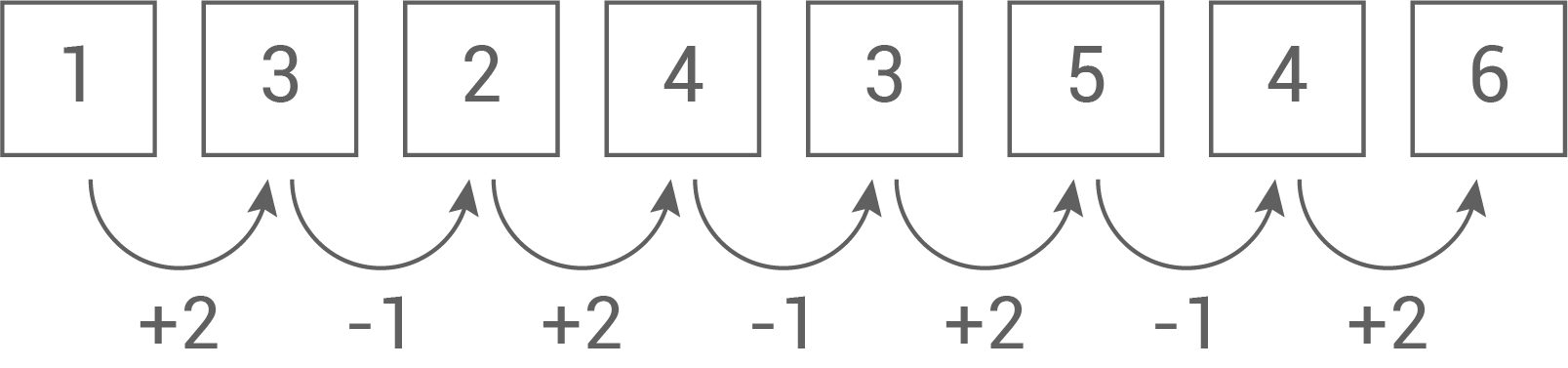
Die Zahlenreihe folgt einer bestimmten Regel. Ergänze die nächsten beiden Zahlen.

hauptschulabschluss mathe 2017 baden-württemberg

(1 Pkt.)

In einer 9. Klasse haben 6 Schüler ihre Körpergröße gemessen:

Timur	$1,76 \,\text{m}$
Dorian	$167 \,\text{cm}$
Mirco	$1,62 \,\text{m}$
Adrian	$173 \,\text{cm}$
Onur	$1,78 \,\text{m}$
Philip	$1,82 \,\text{m}$

Berechne die durchschnittliche Körpergröße dieser Schüler.

(1 Pkt.)

Löse die Gleichung.
$15,5 x+44-4,5 x=6 x-11$

(1 Pkt.)

In der Skizze siehst du eine Korkplatte.

HSA 2017 BAWÜ Fläche Länge Strecke Rechteck

Wie viele Korkplatten werden für $1 \,\text{m}^2$ benötigt?

(1 Pkt.)

Zeichne mithilfe von Zirkel und Geodreieck ein Kreisdiagramm zu folgender Aussage:
„4 von 9 Schülern tragen eine Brille.“

(1 Pkt.)

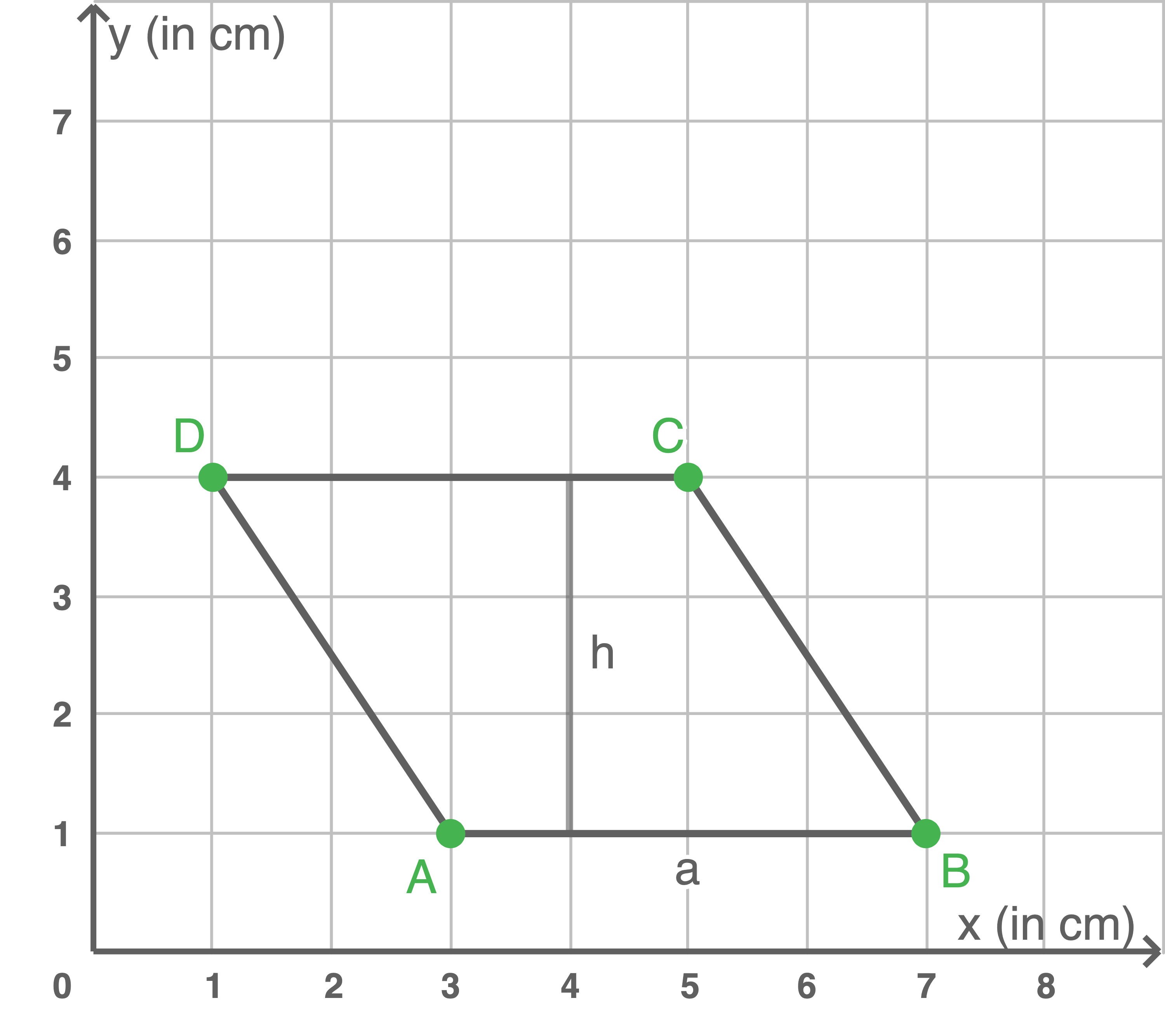
Zeichne ein Viereck mit den Punkten $A(3\mid 1);$ $B(7\mid 1);$ $C(5 \mid 4)$ und $D(1 \mid 4)$ in das Koordinatensystem ein.

Gib den Flächeninhalt der Figur in $\,\text{cm}^2$ an.

10.

Das Würfelbauwerk soll zum kleinsten Quader ergänzt werden, ohne die Lage der vorhandenen Würfel zu verändern.
Wie viele Würfel fehlen?

(1 Pkt.)

Ersparnis bei Angebot A

$120\,€-99\,€=\boldsymbol{21\,€}$

Ersparnis bei Angebot B

$:100$

$\cdot 15$ Grau geschwungener Pfeil, der nach rechts unten zeigt.

$\begin{array}{rcl} 100\,\% & \mathrel{\widehat{=}}& 120\,€ \\[5pt] 1\,\% & \mathrel{\widehat{=}}& 1,20\,€ \\[5pt] 15\,\% & \mathrel{\widehat{=}}& \boldsymbol{18\,€} \\[5pt] \end{array}$

$:100$

$\cdot 15$

Bei Angebot A spart man mehr Geld.

	$\dfrac{1}{2} \cdot \dfrac{1}{2}$
	$\dfrac{1}{3}-\dfrac{1}{3}-\dfrac{1}{3}$
	$\dfrac{1}{8}: \dfrac{1}{8}$
	$\dfrac{1}{5}+\dfrac{1}{5}+\dfrac{1}{5}+\dfrac{1}{5}$

Rechnungen

$\dfrac{1}{2} \cdot \dfrac{1}{2}=\dfrac{1}{4}$
$\dfrac{1}{3}-\dfrac{1}{3}-\dfrac{1}{3}=-\dfrac{1}{3}$
$\dfrac{1}{8}: \dfrac{1}{8}=\dfrac{1}{8}\cdot8=\dfrac{8}{8}=1$
$\dfrac{1}{5}+\dfrac{1}{5}+\dfrac{1}{5}+\dfrac{1}{5}=\dfrac{4}{5}$

$\quad 10^4 \cdot\left(8 \dfrac{1}{5}-1,7\right)$

$\begin{array}[t]{rll} &=& 10\,000 \cdot\left(8 \dfrac{1}{5}-1,7\right) \\[5pt] &=& 10\,000 \cdot\left(8 \dfrac{2}{10}-1,7\right) \\[5pt] &=& 10\,000 \cdot(8+ 0,2-1,7) \\[5pt] &=& 10\,000 \cdot6,5 \\[5pt] &=& 65\,000 \end{array}$

Um den Durchschnitt zu berechnen, müssen alle Größen in die gleiche Einheit umgerechnet werden, z.B. $\text{cm}$ oder $\text{m}.$

Rechenweg anzeigen

Die durchschnittliche Körpergröße beträgt $1,73\,\text{m}.$

$\begin{array}[t]{rll} 15,5x+44-4,5x&=&6x-11 \\[5pt] 11x+44&=&6x-11 &\quad \scriptsize \mid\;-6x \\[5pt] 5x+44&=&-11 &\quad \scriptsize \mid\;-44 \\[5pt] 5x&=&-55 &\quad \scriptsize \mid\;:5 \\[5pt] x&=&-11 \end{array}$

Flächeninhalt einer Korkplatte berechnen

$\begin{array}[t]{rll} A&=&a\cdot b \\[5pt] A&=&25\,\text{cm} \cdot 20\,\text{cm} \\[5pt] A&=&500\,\text{cm}^2 \\[5pt] \end{array}$

Anzahl der Korkplatten berechnen

Quadratmeter in Quadratzentimeter umrechnen: $1\,\text{m}^2=100\,\text{dm}^2=10\,000\,\text{cm}^2$

Benötigte Korkplatten: $10\,000\,\text{cm}^2:500\,\text{cm}^2=20$

Es werden 20 Korkplatten gebraucht.

Für das Zeichnen werden die Mittelpunktswinkel benötigt:

Mittelpunktswinkel für das Segment „Schüler mit Brille“

$:9$

$\cdot 4$

$\begin{array}{rcl} 9\,\text{Schüler} & \mathrel{\widehat{=}}& 360^{\circ}\\[5pt] 1\,\text{Schüler} & \mathrel{\widehat{=}}& 40^{\circ}\\[5pt] 4\,\text{Schüler} & \mathrel{\widehat{=}}& 160^{\circ}\\[5pt] \end{array}$

$:9$

$\cdot 4$

Mittelpunktswinkel für das Segment „Schüler ohne Brille“

$:9$

$\cdot 4$

$\begin{array}{rcl} 9\,\text{Schüler} & \mathrel{\widehat{=}}& 360^{\circ}\\[5pt] 1\,\text{Schüler} & \mathrel{\widehat{=}}& 40^{\circ}\\[5pt] 5\,\text{Schüler} & \mathrel{\widehat{=}}& 200^{\circ}\\[5pt] \end{array}$

$:9$

$\cdot 4$

Kreisdiagramm zeichnen

Flächeninhalt des Parallelogramms berechnen

$\begin{array}[t]{rll} A&=& a\cdot h \\[5pt] A&=& 4\,\text{cm}\cdot 3\,\text{cm} \\[5pt] A&=& 12\,\text{cm}^2 \end{array}$

10.

Der fertige Quader hat dann folgende Maße:

4 Würfel lang
4 Würfel tief
3 Würfel hoch

Gesamtanzahl der Würfel: $4\cdot 4\cdot 3=48$

Bereits vorhandene Würfel: $9$

Es fehlen also noch $48\,\text{Würfel}-9\,\text{Würfel}=\boldsymbol{39}$ Würfel.