Wahlteil B
Aufgabe 1
a)
Ein zylinderförmiger Wasserbehälter ist zu  mit Wasser gefüllt.
mit Wasser gefüllt.
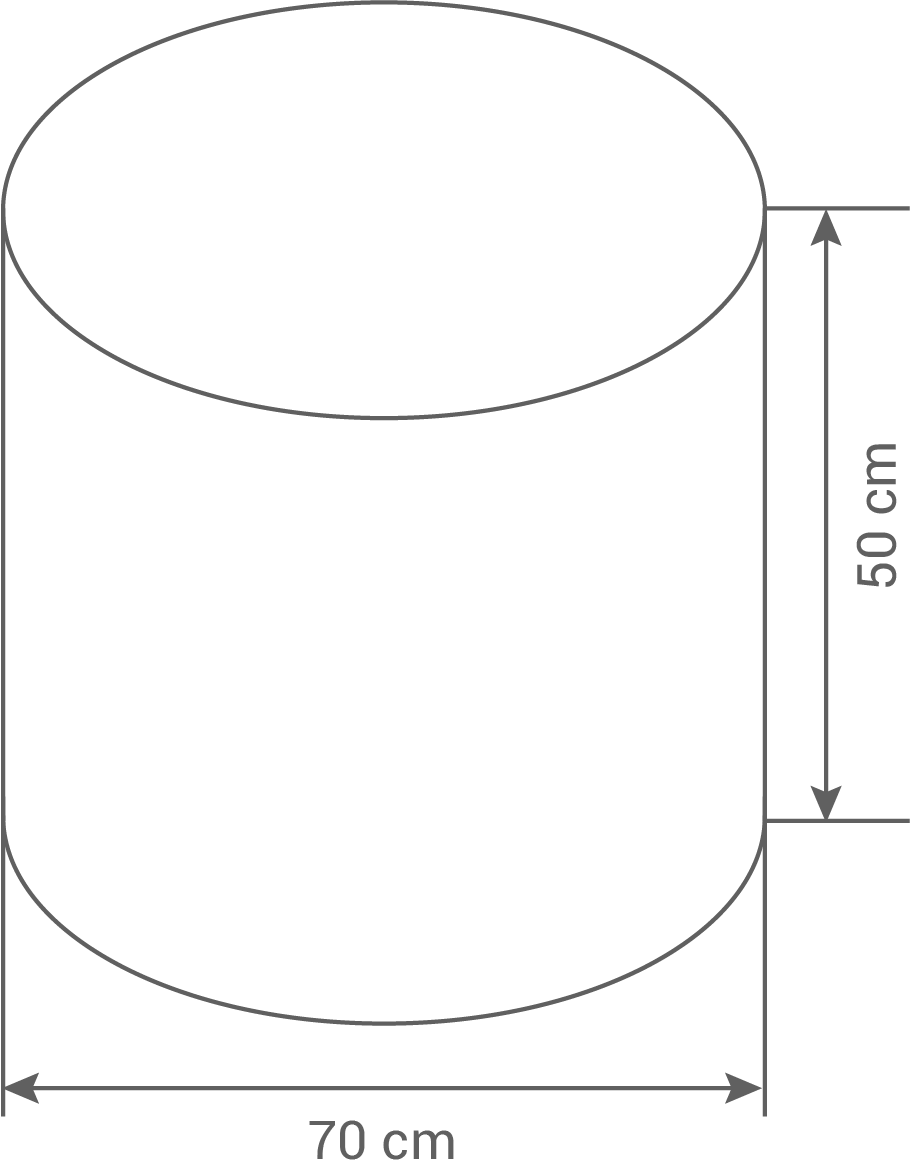 Wie viele
Wie viele  Wasser befinden sich in dem Behälter?
Wasser befinden sich in dem Behälter?

Zeichnung nicht maßstabsgetreu
(3 Pkt.)
b)
Ein quaderförmiger Behälter soll das Volumen von  haben.
Gib eine Möglichkeit für die Maße des Behälters an.
haben.
Gib eine Möglichkeit für die Maße des Behälters an.
Bedingung: Kein Maß darf kleiner als sein.
sein.
Bedingung: Kein Maß darf kleiner als
(2 Pkt.)
Aufgabe 2
a)
Zeichne das Dreieck mit den Maßen  ,
,  und
und 
Ermittle die Winkelgrößen und
und 
Ermittle die Winkelgrößen
(2 Pkt.)
b)
Berechne den Flächeninhalt deines gezeichneten Dreiecks.
Entnimm die nötigen Maße deiner Zeichnung.
Zeichne ein Dreieck mit dem gleichen Flächeninhalt, bei dem die Seite  lang ist.
lang ist.
Entnimm die nötigen Maße deiner Zeichnung.
(3 Pkt.)
Aufgabe 3
a)
Die Klassen 9a und 10b planen jeweils einen Ausflug.
Jede Klasse benötigt dazu einen Kleintransporter.
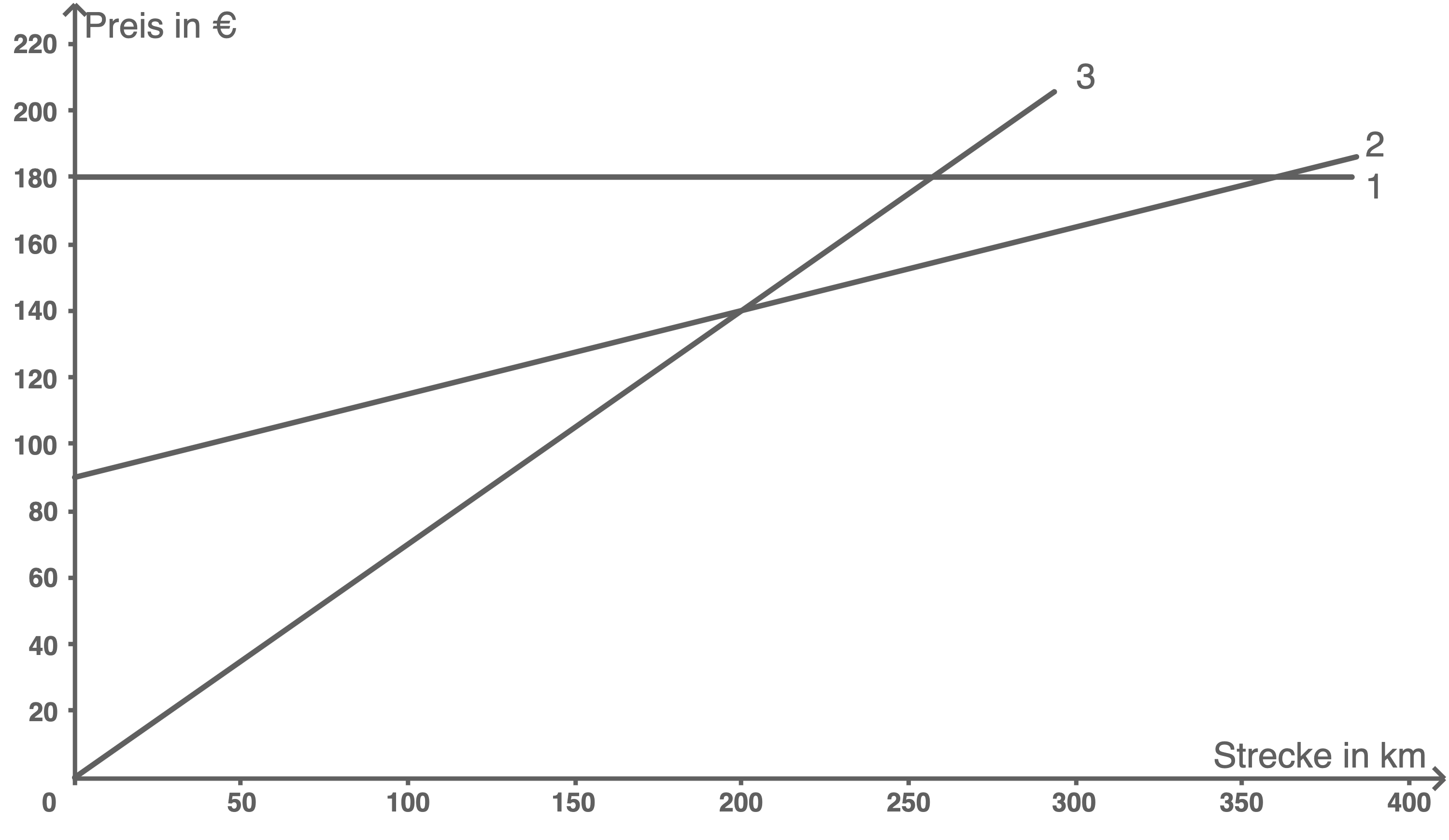
Im Internet finden sie folgende Angebote:
 Wertetabelle A
Wertetabelle A
Wertetabelle B
Wertetabelle C
Jede Klasse benötigt dazu einen Kleintransporter.
Im Internet finden sie folgende Angebote:
Firma Schnell
- Grundpreis:
- Preis pro gefahrenem Kilometer:
Firma Flott
- Kein Grundpreis
- Preis pro gefahrenem Kilometer:
Firma Eilig
- Preis:
- Ordne die drei Angebote den entsprechenden Graphen zu.
- Ordne die drei Angebote den entsprechenden Wertetabellen zu.

| Strecke (km) | |||
|---|---|---|---|
| Preis (€) |
| Strecke (km) | |||
|---|---|---|---|
| Preis (€) |
| Strecke (km) | |||
|---|---|---|---|
| Preis (€) |
(2 Pkt.)
b)
- Die Klasse 9a wird bei ihrem Ausflug voraussichtlich
zurücklegen.
Welches Angebot ist am günstigsten? Begründe deine Entscheidung. - Die Klasse 10b möchte nicht mehr als
für den Kleintransporter ausgeben.
Welche Strecke können sie maximal zurücklegen? Begründe rechnerisch.
(3 Pkt.)
Lösung 1
a)
Gesamtes Volumen des Zylinders berechnen
![\(\begin{array}[t]{rll}
V&=&\pi\cdot r^2\cdot h \\[5pt]
V&=&\pi\cdot(35\,\text{cm})^2\cdot50\,\text{cm} \\[5pt]
V&\approx&192\,422,55\,\text{cm}^3
\end{array}\)](https://www.schullv.de/resources/formulas/dc63adcdf0c1e8fa3479e675c4d64642106738140ee465519a4919fac84940f1_light.svg) 95 % des Volumen berechnen
95 % des Volumen berechnen
 Wasser im Behälter.
Wasser im Behälter.
Lösungsweg über den Dreisatz




![\(\begin{array}{rcl}
100\,\% & \mathrel{\widehat{=}}& 192\,422,55\\[5pt]
1\,\% & \mathrel{\widehat{=}}& \dfrac{192\,422,55}{100} \\[5pt]
95\,\% & \mathrel{\widehat{=}}& \dfrac{192\,422,55}{100}\cdot 95
\end{array}\)](https://www.schullv.de/resources/formulas/56b2d17750aa9eab55ba7d3c788ae1c2eb839301d63272b6e5ed596db58fe9d3_light.svg)





Lösungsweg über die Formel
![\(\begin{array}[t]{rll}
P&=&\dfrac{G\cdot p}{100} \\[5pt]
P&=& \dfrac{192\,422,55\,\text{cm}^3\cdot95}{100} \\[5pt]
P&\approx&182\,801\,\text{cm}^3
\end{array}\)](https://www.schullv.de/resources/formulas/3c4279601b6f37db8b25a4509732cd58aca8c4256b406fe1d41b016ac59c11e1_light.svg)
Es befinden sich
b)
Überlegungen:
 Eine mögliche Lösung:
Eine mögliche Lösung: 
- Formel zur Berechnung des Volumen in einem Quader:
- Es werden also drei Zahlen gesucht, die miteinander multipliziert
ergeben.
umgerechnet:
- Kein Maß darf kleiner als
sein.
Lösung 2
a)
Dreieck zeichnen
Konstruktionsschritte
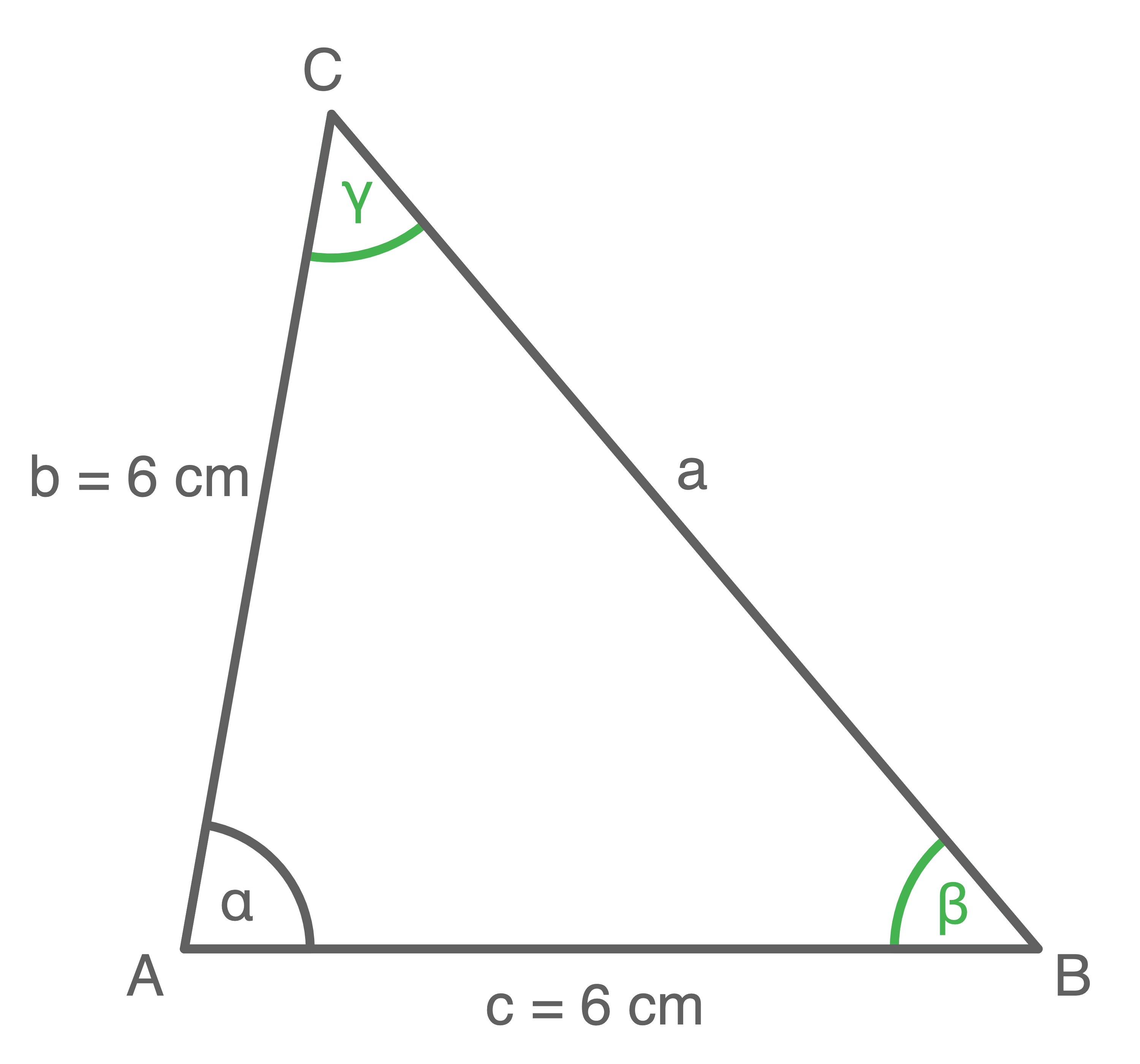 Fehlende Winkelgrößen ermitteln
Da das Dreieck gleichschenklig ist, müssen die Winkel
Fehlende Winkelgrößen ermitteln
Da das Dreieck gleichschenklig ist, müssen die Winkel  und
und  gleich groß sein:
gleich groß sein:  Alternativ können die Winkelgrößen auch in der Zeichnung abgemessen werden.
Alternativ können die Winkelgrößen auch in der Zeichnung abgemessen werden.
- Seite
zeichnen.
- Winkel
in
einzeichnen.
- Länge der Seite
abmessen und
einzeichnen.

b)
Flächeninhalt des gezeichneten Dreiecks berechnen
Um den Flächeninhalt eines Dreiecks zu berechnen, werden die Länge einer Seite und die dazugehörige Höhe benötigt.
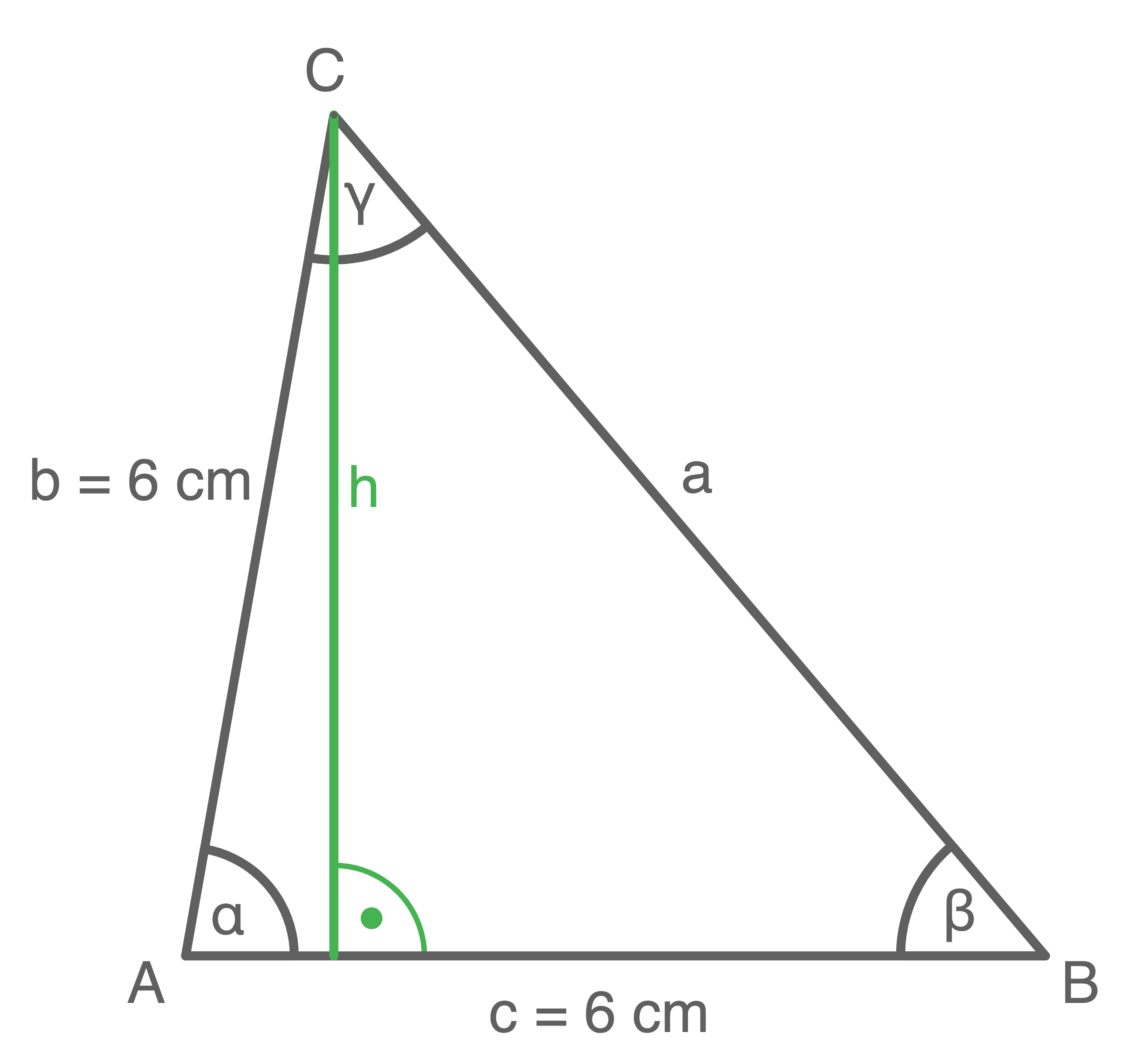 Die Länge der Seite
Die Länge der Seite  ist bereits gegeben:
ist bereits gegeben: 
Die Höhe erhält man durch Abmessen:
erhält man durch Abmessen:  Je nach Bildschirmgröße kann die Messung variieren. Die Vorgehensweise bleibt jedoch die gleiche.
Damit lässt sich nun der Flächeninhalt berechnen:
Je nach Bildschirmgröße kann die Messung variieren. Die Vorgehensweise bleibt jedoch die gleiche.
Damit lässt sich nun der Flächeninhalt berechnen:
![\(\begin{array}[t]{rll}
A&=&\dfrac{c\cdot h}{2} \\[5pt]
A&=&\dfrac{6\,\text{cm}\cdot 5,8\,\text{cm}}{2} \\[5pt]
A&=&17,4\,\text{cm}^2
\end{array}\)](https://www.schullv.de/resources/formulas/c9046a13704bb88f31faa86e1b03fc899b0d7404c1e2d53899e71168420dfb48_light.svg) Weiteres Dreieck zeichnen
Um das Dreieck zeichnen zu können, wird die Höhe benötigt. Diese erhält man durch Umstellung der Formel zur Berechnung des Flächeninhalts:
Weiteres Dreieck zeichnen
Um das Dreieck zeichnen zu können, wird die Höhe benötigt. Diese erhält man durch Umstellung der Formel zur Berechnung des Flächeninhalts:
![\(\begin{array}[t]{rll}
A&=&\dfrac{c\cdot h}{2} &\quad \scriptsize \mid\;\cdot2 \\[5pt]
2\cdot A&=&c\cdot h&\quad \scriptsize \mid\;:c \\[5pt]
\dfrac{2\cdot A}{c}&=&h \ \\[5pt]
h&=&\dfrac{2\cdot A}{c} \ \\[5pt]
h&=& \dfrac{2\cdot 17,4\,\text{cm}^2}{10\,\text{cm}} \\[5pt]
h&=&3,48\,\text{cm}\approx3,5\,\text{cm}
\end{array}\)](https://www.schullv.de/resources/formulas/bee044921f45503954be468af32da6dc9a3ef5acf06ff61d220ffb1e6785b71f_light.svg) Mit der Seitenlänge
Mit der Seitenlänge  und der Höhe
und der Höhe  kann das Dreieck gezeichnet werden.
Eine mögliche Lösung:
kann das Dreieck gezeichnet werden.
Eine mögliche Lösung:
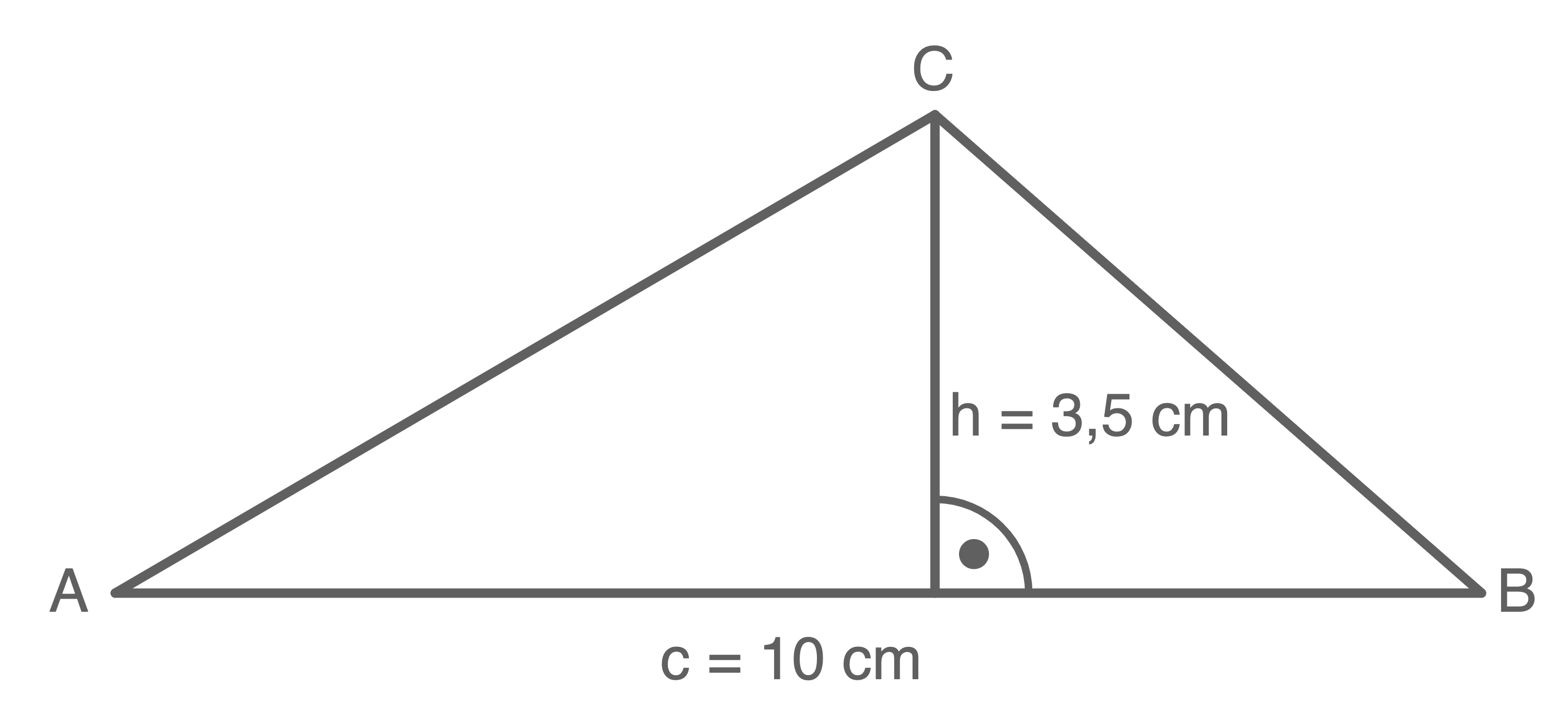 Die Höhe
Die Höhe  kann an einer beliebigen Stelle eingezeichnet werden.
kann an einer beliebigen Stelle eingezeichnet werden.

Die Höhe

Lösung 3
a)
Angebote den Graphen zuordnen
- Firma Schnell: Graph 2
- Firma Flott: Graph 3
- Firma Eilig: Graph 1
- Firma Schnell: Wertetabelle C
- Firma Flott: Wertetabelle B
- Firma Eilig: Wertetabelle A
b)
Welches Angebot ist am günstigsten?
Firma Schnell bietet das günstigste Angebot an, da der dazugehörige Graph 2 bei  am niedrigsten ist.
Welche Strecke können sie maximal zurücklegen?
Da Firma Schnell bei
am niedrigsten ist.
Welche Strecke können sie maximal zurücklegen?
Da Firma Schnell bei  und Firma Eilig bereits bei
und Firma Eilig bereits bei  starten, kommt für die Klasse 10b nur das Angebot der Firma Flott in Frage.
starten, kommt für die Klasse 10b nur das Angebot der Firma Flott in Frage.
Mit dieser Info kann ausgerechnet werden, wie viele Kilometer gefahren werden können: Die Klasse 10b kann maximal
Die Klasse 10b kann maximal  zurücklegen.
zurücklegen.
Mit dieser Info kann ausgerechnet werden, wie viele Kilometer gefahren werden können: