Grundkenntnisse
1.
Kreuze das größte Produkt an.
(1 Pkt.)
2.
Markiere die folgenden Zahlen möglichst genau auf dem Zahlenstrahl.
a)
b)
(1 Pkt.)
3.
Innerhalb weniger Tage steigt die Temperatur um 8 Grad Celsius an.
Welche Temperatur zeigt das Thermometer nach dem Temperaturanstieg?
Welche Temperatur zeigt das Thermometer nach dem Temperaturanstieg?
(1 Pkt.)
4.
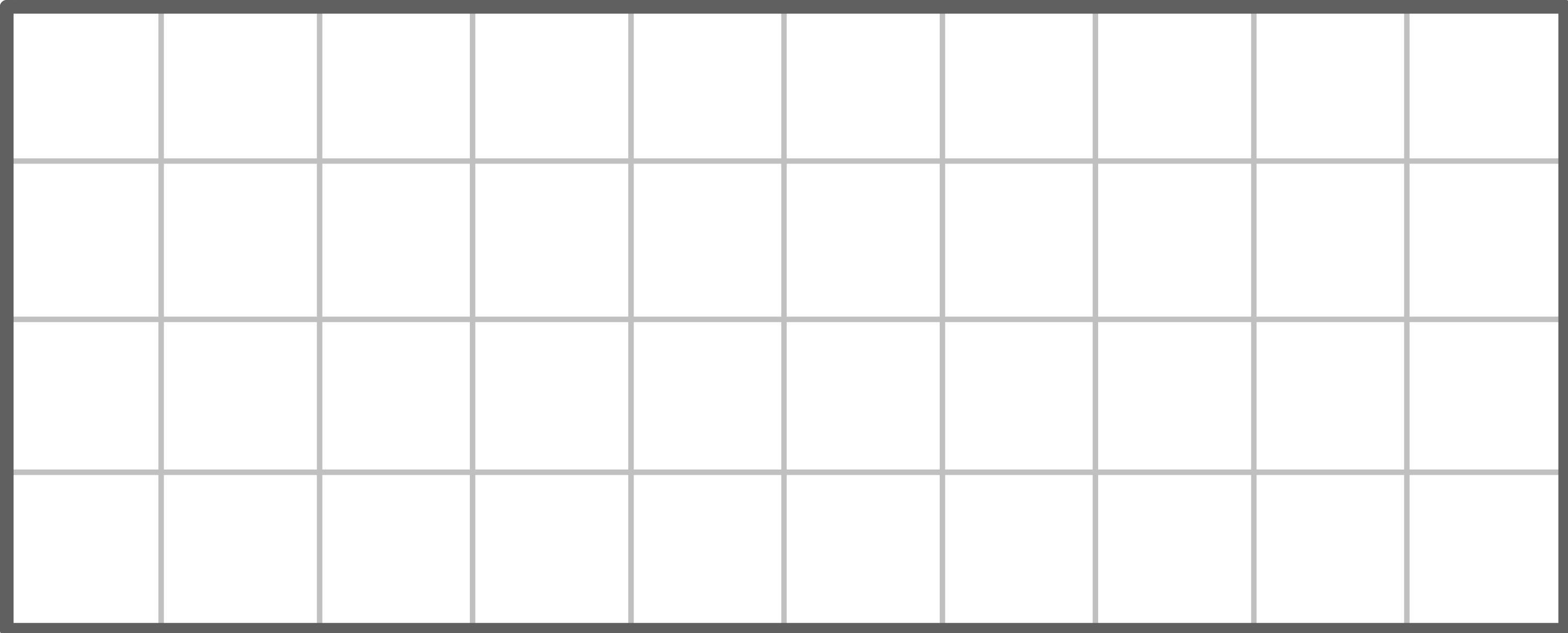
Schraffiere zunächst 
des Rechtecks.
Male dann
der schraffierten Fläche an.
Male dann
(1 Pkt.)
5.
Ein Parkhaus hat 350 Plätze. 140 Plätze sind noch frei.
Wie viel Prozent der Plätze sind noch frei?
Wie viel Prozent der Plätze sind noch frei?
(1 Pkt.)
6.
Wie groß ist der Winkel 
?
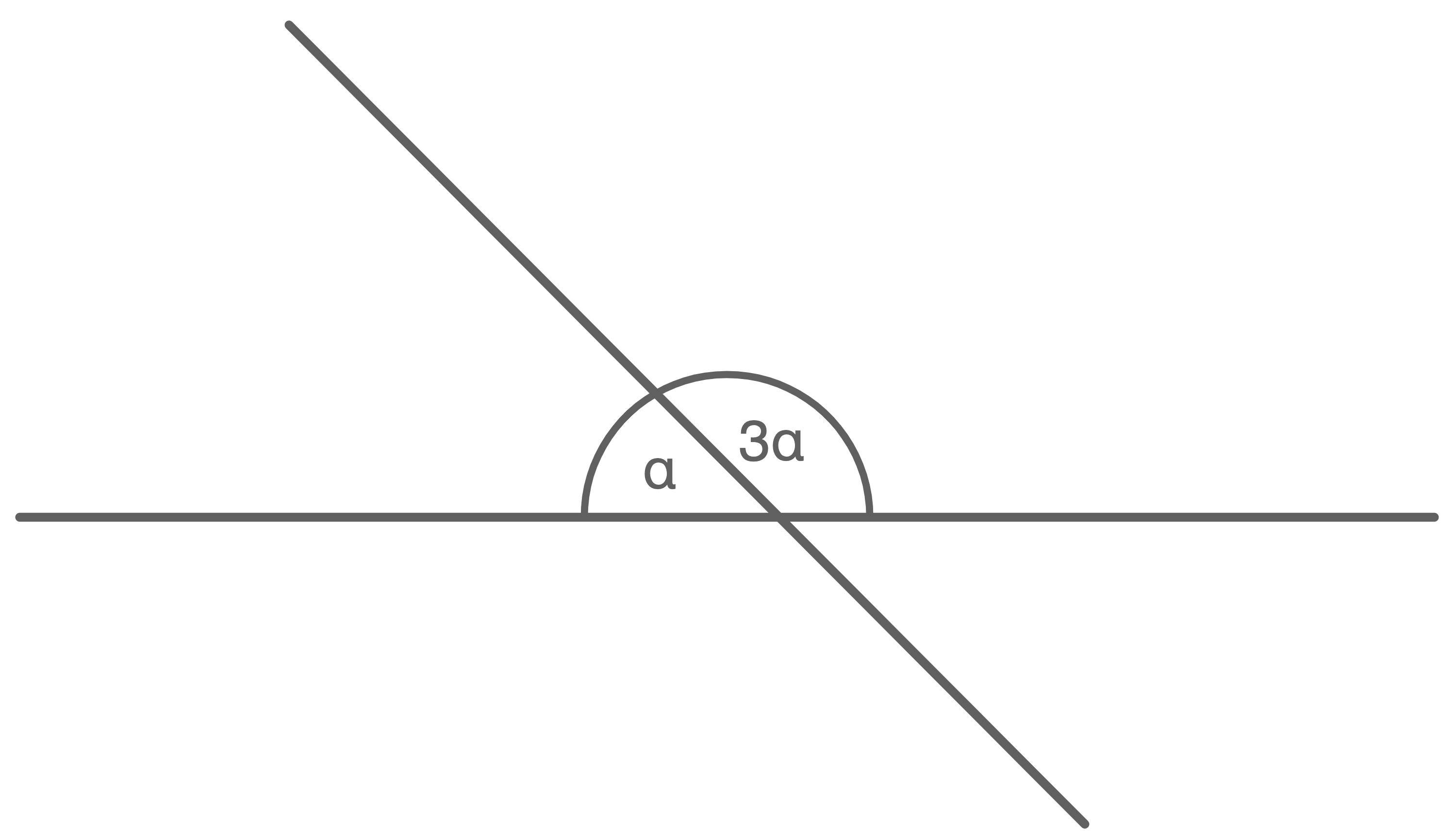
Zeichnung nicht maßstabsgtreu
(1 Pkt.)
7.
Löse die Gleichung.
(1 Pkt.)
8.
Aus wie vielen Würfeln besteht diese Figur?
(1 Pkt.)
9.
Welche der beiden Figuren hat den größeren Flächeninhalt?
Entnimm die Maße den Zeichnungen und begründe rechnerisch.
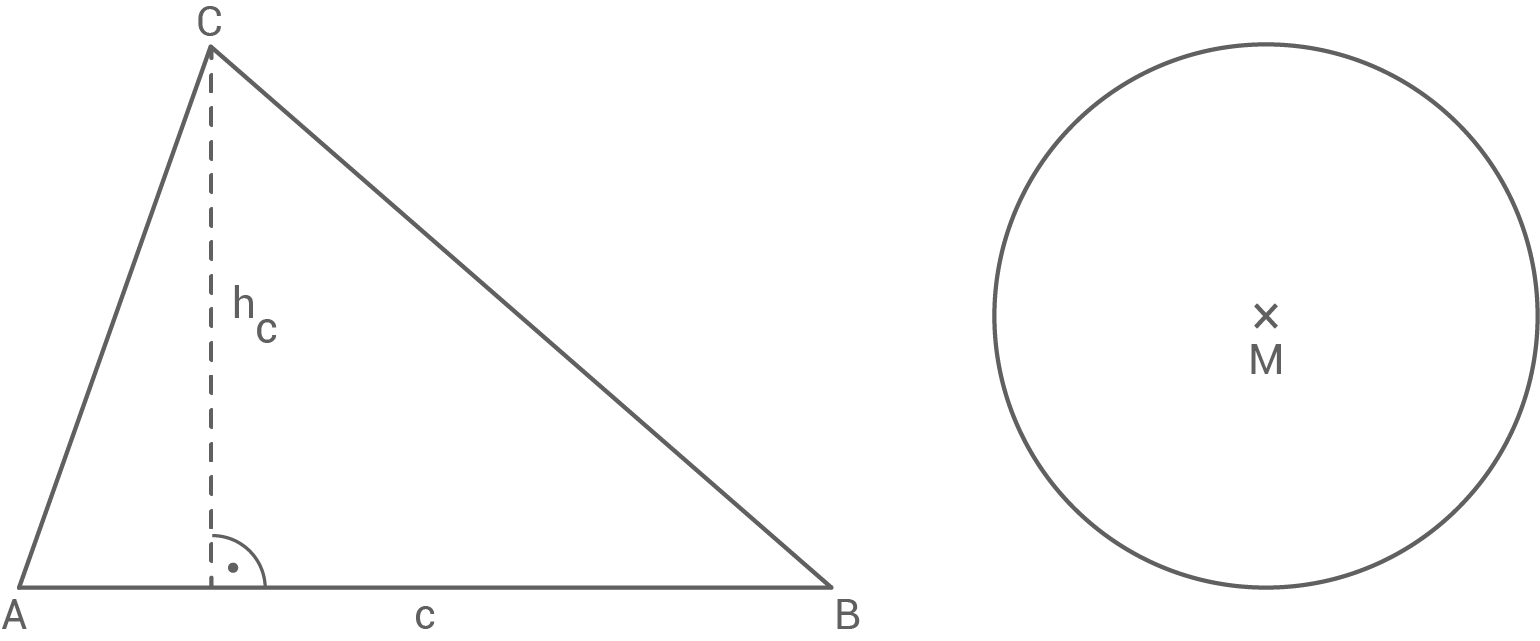
Entnimm die Maße den Zeichnungen und begründe rechnerisch.
(1 Pkt.)
10.
Es wird einmal verdeckt gezogen. Kreuze jeweils richtig oder falsch an.
| wahr | falsch | |||
| Die Wahrscheinlichkeit, einen Kreis zu ziehen, liegt bei |
|
|
||
| Die Wahrscheinlichkeit, einen Kreis zu ziehen, ist genauso groß, wie die Wahrscheinlichkeit, ein Dreieck zu ziehen. |
|
|
||
| Die Wahrscheinlichkeit, ein Dreieck zu ziehen, liegt bei |
|
|
||
| Die Chance, ein Quadrat zu ziehen, liegt bei |
|
|
(1 Pkt.)
1.
2.
a)
b)
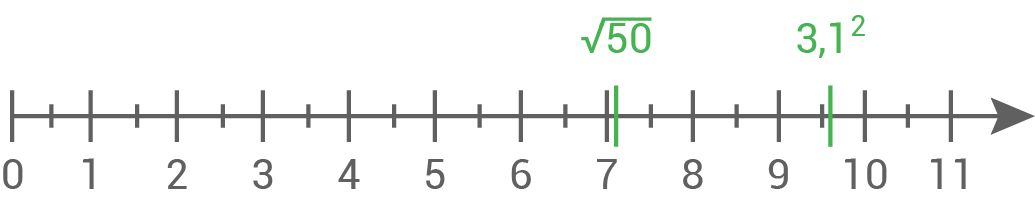
3.
Die Anfangstemperatur beträgt 
Nach dem Temperaturanstieg zeigt das Thermometer 
4.
Es gibt insgesamt
Es gibt insgesamt
5.
6.
Da sich Nebenwinkel zu 
ergänzen lassen, kann folgende Gleichung aufgestellt werden:
![\(\begin{array}[t]{rll}
\alpha+3\alpha&=&180^{\circ} \\[5pt]
4\alpha&=&180^{\circ} &\quad \scriptsize \mid\;:4 \\[5pt]
\alpha&=&\dfrac{180^{\circ}}{4^{\circ}} \\[5pt]
\alpha&=&45^{\circ}
\end{array}\)](https://mathjax.schullv.de/a87dad4e3dbae17807c5091527896832b91720ef3269635d46d3d1864c80670c?color=5a5a5a)
7.
8.
Die Figur besteht aus 84 Würfeln.
9.
Flächeninhalt des Dreiecks berechnen
Durch Abmessen erhält man:
![\(\begin{array}[t]{rll}
A_1&=&\dfrac{c\cdot h_c}{2} \\[5pt]
A_1&=&\dfrac{6\,\text{cm}\cdot 4\,\text{cm}}{2} \\[5pt]
A_1&=&3\,\text{cm}\cdot 4\,\text{cm} \\[5pt]
A_1&=&12\,\text{cm}^2 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/2fc1229fa0a7a9e6ad6aa2240f26cecb64c21cc8d91309a7f3c79e8dd2e7ee91?color=5a5a5a)
Flächeninhalt des Kreises berechnen
Durch Abmessen erhält man:
![\(\begin{array}[t]{rll}
A_2&=&\pi\cdot r^2 \\[5pt]
A_2&=&\pi\cdot (2\,\text{cm})^2 \\[5pt]
A_2&\approx&3,14\cdot (2\,\text{cm})^2 \\[5pt]
A_2&=&3,14\cdot 4\,\text{cm}^2 \\[5pt]
A_2&=&12,56\,\text{cm}^2 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/7649adb31f2f02ff116290fa3ed29c73117ac117562635d43957599187267e8a?color=5a5a5a)
Der Flächeninhalt des Kreises ist größer.
10.
| wahr | falsch | |||
| Die Wahrscheinlichkeit, einen Kreis zu ziehen, liegt bei |
|
|
||
| Die Wahrscheinlichkeit, einen Kreis zu ziehen, ist genauso groß, wie die Wahrscheinlichkeit, ein Dreieck zu ziehen. |
|
|
||
| Die Wahrscheinlichkeit, ein Dreieck zu ziehen, liegt bei |
|
|
||
| Die Chance, ein Quadrat zu ziehen, liegt bei |
|
|
Es gibt 8 Figuren. Damit die Wahrscheinlichkeit, einen Kreis zu ziehen, bei
Da es genauso viele Dreiecke wie Kreise gibt, sind die Wahrscheinlichkeiten gleich groß. Aussage 3
Damit die Wahrscheinlichkeit, ein Dreieck zu ziehen, bei
Es gibt insgesamt 8 Figuren. Davon sind 2 Quadrate. Die Wahrscheinlichkeit, ein Quadrat zu ziehen, beträgt also