Aufgabe 4.1 - Analysis
Gegeben ist eine in  definierte ganzrationale Funktion
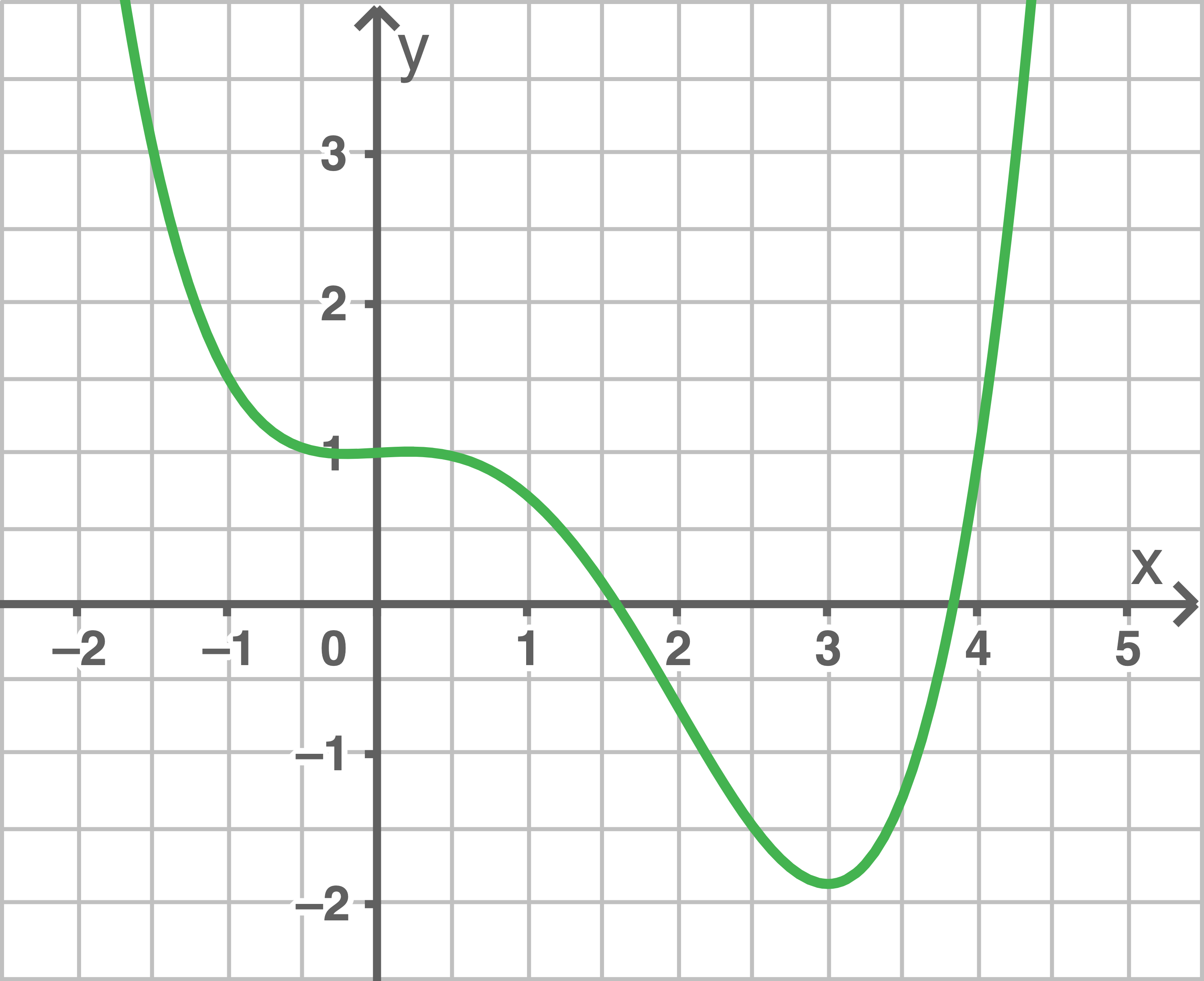
definierte ganzrationale Funktion  vierten Grades. Die Abbildung zeigt den Graphen der Funktion
vierten Grades. Die Abbildung zeigt den Graphen der Funktion 

a)
Ermittle  und deute das Ergebnis geometrisch.
und deute das Ergebnis geometrisch.
(2 BE)
b)
Der Graph der Ableitungsfunktion  besitzt einen lokalen Hochpunkt.
besitzt einen lokalen Hochpunkt.
Gib die -Koordinate dieses Extrempunkts an und begründe mithilfe von Eigenschaften der Funktion
-Koordinate dieses Extrempunkts an und begründe mithilfe von Eigenschaften der Funktion  bzw. ihres Graphen, dass dieser Extrempunkt ein Hochpunkt ist.
bzw. ihres Graphen, dass dieser Extrempunkt ein Hochpunkt ist.
Gib die
(3 BE)
c)
Ermittle den Wert des Terms 
(2 BE)
d)
Die Funktion  hat die Nullstellen
hat die Nullstellen  und
und  mit
mit 
Begründe, dass der Wert des Terms negativ ist.
negativ ist.
Begründe, dass der Wert des Terms
(3 BE)
a)
Die Gerade durch die beiden Punkte  und
und  besitzt die Steigung
besitzt die Steigung  Dies ist auch die mittlere Änderungsrate der Funktion
Dies ist auch die mittlere Änderungsrate der Funktion  im Intervall
im Intervall ![\([-1,5;0].\)](https://mathjax.schullv.de/313cee1fb5b0a4604b43b12d574ef7008869645ac6f113aa5e95ce806e005867?color=5a5a5a)
b)
Die Extremstellen von  entsprechen den Wendestellen von
entsprechen den Wendestellen von  Der Abbildung kann man entnehmen, dass der Graph von
Der Abbildung kann man entnehmen, dass der Graph von  beispielsweise bei
beispielsweise bei  eine Wendestelle besitzt. An dieser Stelle geht der Graph von
eine Wendestelle besitzt. An dieser Stelle geht der Graph von  von einer Linkskrümmung in einer Rechtskrümmung über.
von einer Linkskrümmung in einer Rechtskrümmung über.
Der Graph von fällt für
fällt für  streng monoton, fällt aber immer langsamer je weiter er sich der
streng monoton, fällt aber immer langsamer je weiter er sich der  -Achse nähert, bis er schließlich die Steigung Null bei
-Achse nähert, bis er schließlich die Steigung Null bei  erreicht. Anschließend fällt der Graph wieder mit zunehmender Geschwindigkeit. An der Stelle
erreicht. Anschließend fällt der Graph wieder mit zunehmender Geschwindigkeit. An der Stelle  hat die Steigung also ein lokales Maximum angenommen, indem sie kurzzeitig nicht mehr negativ war. Da die Steigung von
hat die Steigung also ein lokales Maximum angenommen, indem sie kurzzeitig nicht mehr negativ war. Da die Steigung von  durch
durch  beschrieben wird, besitzt der Graph von
beschrieben wird, besitzt der Graph von  an dieser Stelle
an dieser Stelle  also ein Hochpunkt.
also ein Hochpunkt.
Der Graph von
c)
d)
Mit  wird der Inhalt der Fläche berechnet die der Graph von
wird der Inhalt der Fläche berechnet die der Graph von  mit der
mit der  -Achse im Bereich
-Achse im Bereich  einschließt. Der Abbildung kann man entnehmen, dass diese Fläche oberhalb der
einschließt. Der Abbildung kann man entnehmen, dass diese Fläche oberhalb der  -Achse liegt, weshalb der Wert des Integrals positiv ist.
-Achse liegt, weshalb der Wert des Integrals positiv ist.
Das Flächenstück, das zum Integral gehört, liegt allerdings unterhalb der
gehört, liegt allerdings unterhalb der  -Achse. Der Integralwert ist dementsprechend negativ. Das Produkt aus einem positiven und einem negativen Faktor ist negativ. Der Wert des angegebenen Terms ist daher negativ.
-Achse. Der Integralwert ist dementsprechend negativ. Das Produkt aus einem positiven und einem negativen Faktor ist negativ. Der Wert des angegebenen Terms ist daher negativ.
Das Flächenstück, das zum Integral