 Ebenengleichung der Ebene E entwickeln
Ebenengleichung der Ebene E entwickeln
In dieser Aufgabe sollst du eine Gleichung der Ebene

in Koordinatenform bestimmen. Bilde dazu als erstes eine Gleichung in Parameterform. Anschließend kannst du mit dem (Kreuz-)Vektorprodukt den Normalenvektor der Ebene berechnen und damit die Ebenengleichung in Koordinatenform berechnen.
1. Schritt: Ebenengleichung in Parameterform
Wähle einen Ortsvektor von einem der drei Punkte als Stützvektor und bilde aus den drei Punkten zwei Verbindungsvektoren, die als Spannvektoren der Ebene verwendet werden können.

 2. Schritt: (Kreuz-) Vektorprodukt berechnen
2. Schritt: (Kreuz-) Vektorprodukt berechnen
Die Formel für das (Kreuz-)Vektorprodukt lautet:
Setze die beide Richtungsvektoren der Ebene

in die Formel ein.
Den Normalenvektor kannst du mit 9 kürzen.
 3. Schritt: Ebenengleichung in Koordinatenform
3. Schritt: Ebenengleichung in Koordinatenform

Setze die Koordinaten von

in die Ebenengleichung ein, um den Parameter

zu berechnen.

Die Ebene

hat die Koordinatengleichung

.
 Parallelität zeigen
Parallelität zeigen
In dieser Aufgabe sollst du zeigen, dass die Ebene

parallel zur

-Achse ist. Du hast zuvor bereits einen Normalenvektor von

bestimmt. Damit eine Achse parallel zur Ebene verläuft, muss sie senkrecht auf dem Normalenvektor stehen. Bestimme also zunächst einen Richtungsvektor der

-Achse und überprüfe, ob dieser senkrecht auf dem Normalenvektor steht. Zwei Vektoren sind senkrecht zueinander, wenn ihr Skalarprodukt Null ist.
Den Richtungsvektor der

-Achse kannst du beispielsweise wie folgt wählen:

-Achse:

Bilde nun das Skalarprodukt mit dem Normalenvektor

.

Die

-Achse verläuft also senkrecht zum Normalenvektor von

und damit parallel zur Ebene

.
 Schnittwinkel zwischen der Ebene
Schnittwinkel zwischen der Ebene  und der
und der  -Ebene berechnen
-Ebene berechnen
Um den Schnittwinkel zwischen zwei Ebenen zu berechnen, kannst du folgende Formel verwenden:
Die Ebenengleichung in Koordinatenform der

-Ebene ist

. Ein Normalenvektor hat somit die Einträge

Den Normalenvektor der Ebene

hast du in einer Aufgabe zuvor schon berechnet.
Jetzt kannst du beide Normalenvektoren in die Formel einsetzen.
Der Schnittwinkel zwischen der Ebene

und der

-Ebene ist ca.

.
 Koordinaten des Punktes
Koordinaten des Punktes  berechnen
berechnen
Du weißt, dass der Punkt

auf der Ebene

liegt. Um die Koordinaten des Punktes zu berechnen, kannst du den Schnittpunkt der Geraden

, die durch den Punkt

geht und den Normalenvektor der

-Ebene als Richtungsvektor hat, mit der Ebene

berechnen. Bilde dazu als erstes die Gerade

und den allgemeinen Punkt der Geraden

, setze diesen Punkt in die Koordinatengleichung der Ebene

ein und berechne die Variable

. Den Wert für

kannst du dann in den allgemeinen Punkt der Geraden

einsetzten und erhältst die Koordinaten des gesuchten Punktes

.
1. Schritt: Geradengleichung von h bestimmen
Die Gerade

verläuft durch den Punkt

und hat den Normalenvektor der

-Ebene als Richtungsvektor.

 2. Schritt: Variable t berechnen
2. Schritt: Variable t berechnen
Setze den allgemeinen Punkt der Geraden

in die Ebenengleichung

ein.
![\(\begin{array}[t]{rll}
-1-5t&=&-26 &\quad \scriptsize \mid\; +1 \\[5pt]
-5t&=&-25 &\quad \scriptsize \mid\; :(-5) \\[5pt]
t&=&5
\end{array}\)](https://www.schullv.de/resources/formulas/4662f60dfe25e84f5a0638acc83578d7bff05fe7633f345a43d854b0197ae1d3_light.svg) 3. Schritt: Koordinaten des Punktes
3. Schritt: Koordinaten des Punktes  berechnen
berechnen
Setze

in den allgemeinen Punkt H ein.

Der Punkt

hat die Koordinaten

.
 Zeigen, dass der Punkt
Zeigen, dass der Punkt  den größten Abstand zur
den größten Abstand zur  -Ebene hat.
-Ebene hat.
Wenn du dir die Skizze anschaust stellst du fest, dass der höchste Punkt auf dem rechten Rand des Körpers sein muss. Um die Koordinaten des Lotpunktes dieses Punktes, der in der Horizontalebene liegt, zu berechnen, musst du zu der

-Koordinate des Mittelpunktes den Radius addieren. Der Punkt D‘ hat somit die Koordinaten

.
Jetz kannst du wie oben vorgehen. Bilde eine Gerade mit dem Punkt

und dem Normalenvektor der Horizontalebene, berechne die Koordinaten des Schnittpunkts der Ebene

mit der Geraden und du erhältst den Punkt, der den größten Abstand zur Horizontalebene hat.


![\(\begin{array}[t]{rll}
4-5r&=&-26 &\quad \scriptsize \mid\; -4 \\[5pt]
-5r&=&-30 &\quad \scriptsize \mid\; :(-5) \\[5pt]
r&=&6
\end{array}\)](https://www.schullv.de/resources/formulas/287c30f489fcb48d595509800b3380dac8c9db7282b1b796b9df025f6c188bd2_light.svg)

Somit hast du nachgewiesen, dass der Punkt

den größten Abstand von der Horizontalebene hat.
 ,
,  und
und  gegeben.
gegeben.
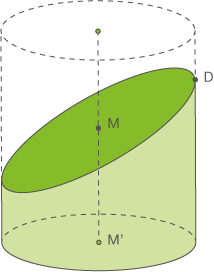 Abb. 1: Abbildung (nicht maßstäblich)
Abb. 1: Abbildung (nicht maßstäblich)
 , die durch die Punkte
, die durch die Punkte  ,
,  und
und  eindeutig bestimmt ist.
eindeutig bestimmt ist.
 -Achse parallel zur Ebene
-Achse parallel zur Ebene  verläuft und berechne das Gradmaß des Schnittwinkels zwischen der Ebene
verläuft und berechne das Gradmaß des Schnittwinkels zwischen der Ebene  und der
und der  -Ebene.
-Ebene.
 ]
]
 geschnitten. Es entsteht ein Körper
geschnitten. Es entsteht ein Körper
 , dessen Lage in dem Koordinatensystem folgendermaßen beschrieben wird:
, dessen Lage in dem Koordinatensystem folgendermaßen beschrieben wird:
 liegt in der
liegt in der  -Ebene und wird durch den Kreis mit dem Mittelpunkt
-Ebene und wird durch den Kreis mit dem Mittelpunkt  und dem Radius
und dem Radius  begrenzt. Die Deckenfläche des Körpers
begrenzt. Die Deckenfläche des Körpers  wird durch die Schnittfigur der Ebene
wird durch die Schnittfigur der Ebene  mit dem geraden Kreiszylinder begrenzt.
mit dem geraden Kreiszylinder begrenzt.
 .
.
 Abb. 1: Abbildung (nicht maßstäblich)
Abb. 1: Abbildung (nicht maßstäblich)
 ist der Fußpunkt des Lotes vom Punkt
ist der Fußpunkt des Lotes vom Punkt  der Ebene
der Ebene  in die
in die  -Ebene. Ermittle die Koordinaten des Punktes
-Ebene. Ermittle die Koordinaten des Punktes  .
.
 liegt in der Deckfläche des Körpers
liegt in der Deckfläche des Körpers  .
.
 von allen Punkten der Deckfläche derjenige Punkt ist, der den größten Abstand zur
von allen Punkten der Deckfläche derjenige Punkt ist, der den größten Abstand zur  -Ebene hat.
-Ebene hat.