Wahlpflichtaufgaben (Aufgabengruppe 1)

4.1

Die Abbildung zeigt den Graphen der in $\mathbb{R}$ definierten Funktion $f$ mit $f (x)=2 \text{e}^x - 2 \text{e}.$

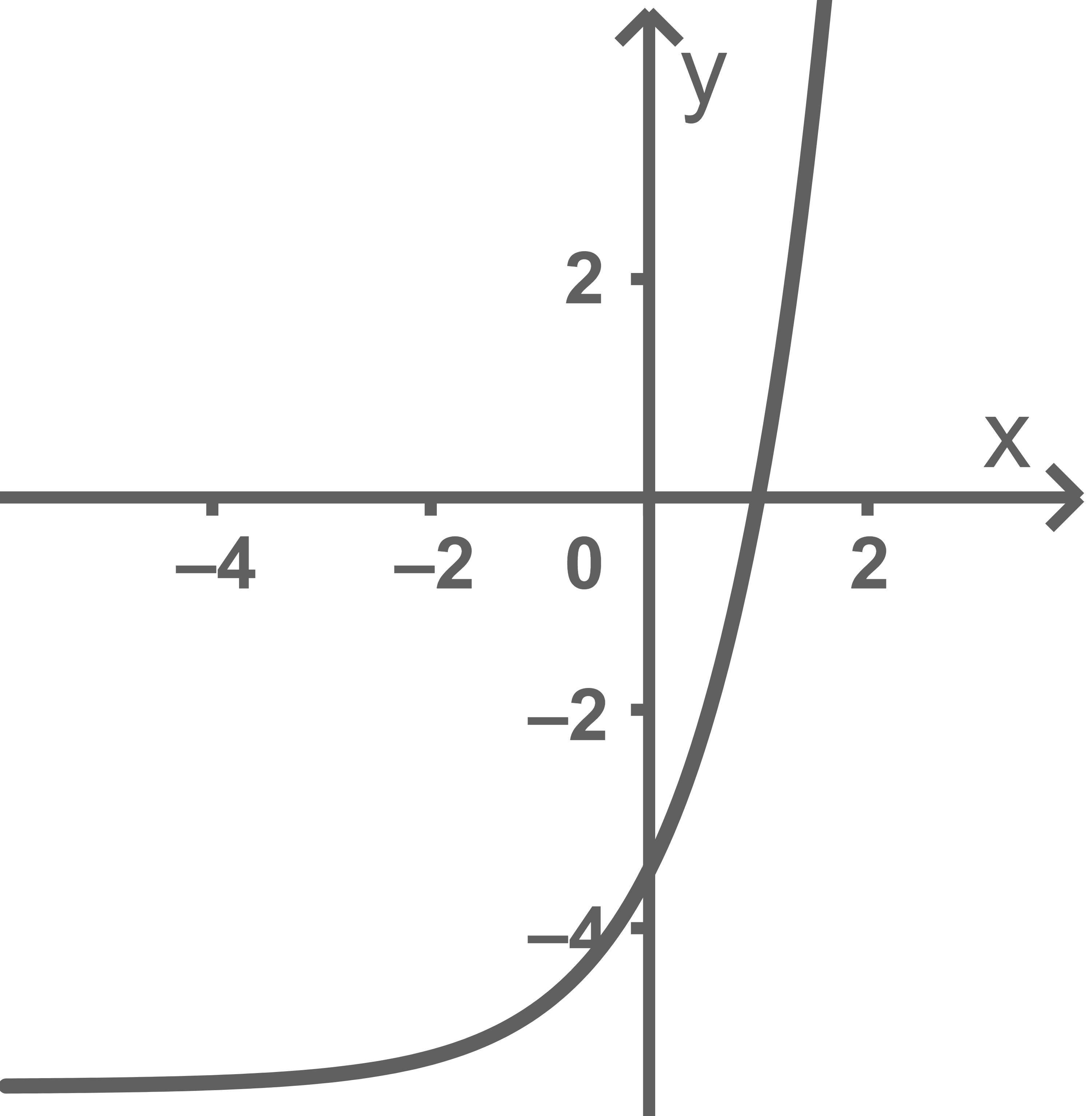
Abbildung

Weise nach, dass $1$ eine Nullstelle von $f$ ist.

(1 BE)

Der Graph von $f$ schließt mit den Koordinatenachsen eine Fläche ein. Berechne ihren Inhalt.

(4 BE)

4.2

Betrachtet werden die Punkte $P \left(3\mid 1 \mid -1\right)$ und $Q\left(4\mid 2 \mid -4\right).$

Begründe, dass die Punkte $P$ und $Q$ auf derselben Seite bezüglich der $xy$ -Ebene liegen.

(1 BE)

Die Punkte $P,Q$ und der Koordinatenursprung $O$ sind die Eckpunkte eines gleichschenkligen Dreiecks, dessen Basis $\overline{OQ}$ die Länge $6$ hat. Ermittle den Flächeninhalt des Dreiecks.

(4 BE)

4.3

Betrachtet wird eine binomialverteilte Zufallsgröße $X\sim B_{n; p}$ mit folgenden Eigenschaften:

Die Standardabweichung von $X$ ist $2.$
$p$ hat den gleichen Wert wie die Wahrscheinlichkeit, beim einmaligen Ziehen unter $1000$ Losen, von denen $800$ keine Gewinnlose sind, ein Gewinnlos zu ziehen.

Ermittle einen Term, mit dem $P \left(X = 10\right)$ berechnet werden kann, und gebe den Wert von $n$ sowie von $p$ an.

(5 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?