Aufgabe 3: Stochastik
In einer Großstadt wurde bei einer Erhebung der Anteil der überbelegten Haushalte an allen Haushalten erfasst. Ein Haushalt gilt als überbelegt, wenn er über zu wenige Zimmer in Bezug auf die Anzahl der im Haushalt lebenden Personen verfügt. In aller Haushalte lebt mindestens ein Kind. Von diesen Haushalten sind
überbelegt. Bei den Haushalten ohne Kind beträgt der Anteil der überbelegten Haushalte
Stelle den Sachverhalt in einem beschrifteten Baumdiagramm dar.
Zeige, dass etwa aller Haushalte überbelegt sind.
Unter allen Haushalten der Großstadt werden Haushalte zufällig ausgewählt. Die Zufallsgröße
beschreibt die Anzahl der überbelegten Haushalte in der Stichprobe und wird als binomialverteilt angenommen.
Beurteile ohne Berechnung von Wahrscheinlichkeiten die folgende Aussage:
Die Wahrscheinlichkeitsverteilung von nimmt für
den größtmöglichen Wert an.
Die Wahrscheinlichkeit dafür, dass von den zufällig ausgewählten Haushalten höchstens
Haushalte überbelegt sind, soll mehr als
betragen.
Ermittle den kleinstmöglichen Wert für
Zwei Jahre später kann davon ausgegangen werden, dass sich in der Großstadt sowohl der Anteil der Haushalte mit mindestens einem Kind als auch der Anteil der überbelegten Haushalte an den Haushalten ohne Kind nicht verändert hat.
Die Abbildung zeigt den Graphen der Funktion mit
und
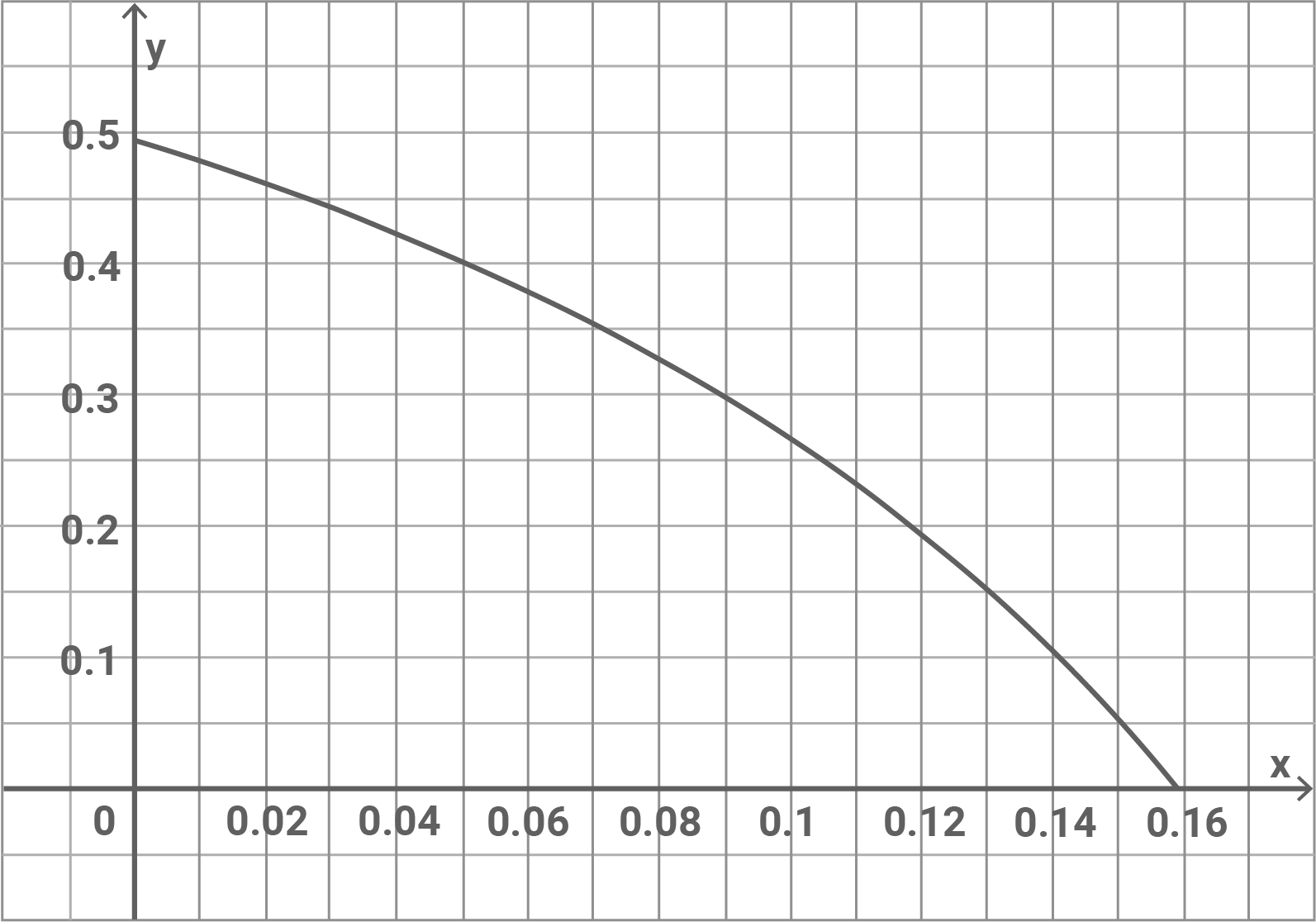
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?Baumdiagramm zum Sachverhalt darstellen
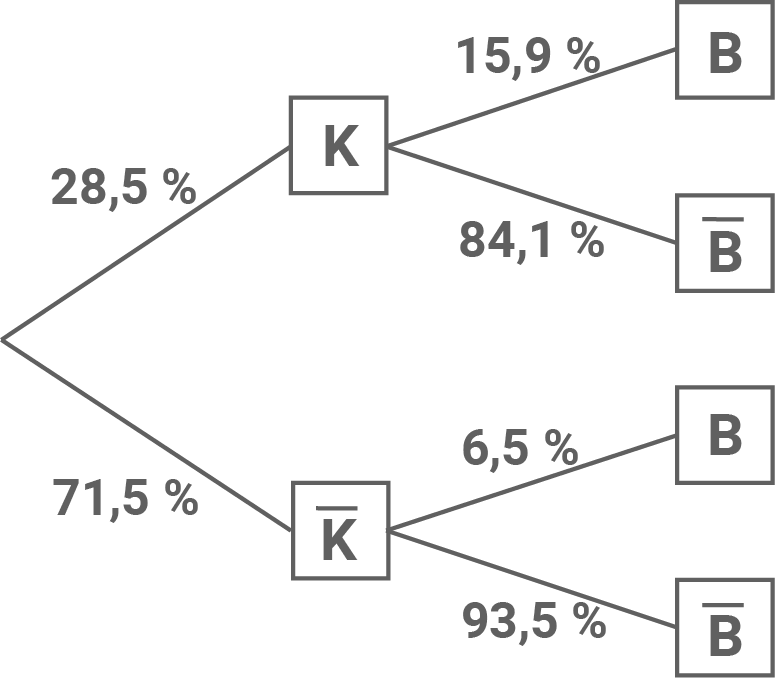
„Im Haushalt lebt mindestens ein Kind.“
„Der Haushalt ist überbelegt.“
Wegen ist die Aussage falsch.
ist binomialverteilt mit den Parametern
und
Systematisches Ausprobieren mit dem Taschenrechner liefert:
Somit ist der kleinstmögliche Wert für
Grafisches Bestimmen, für welchen Wert ist
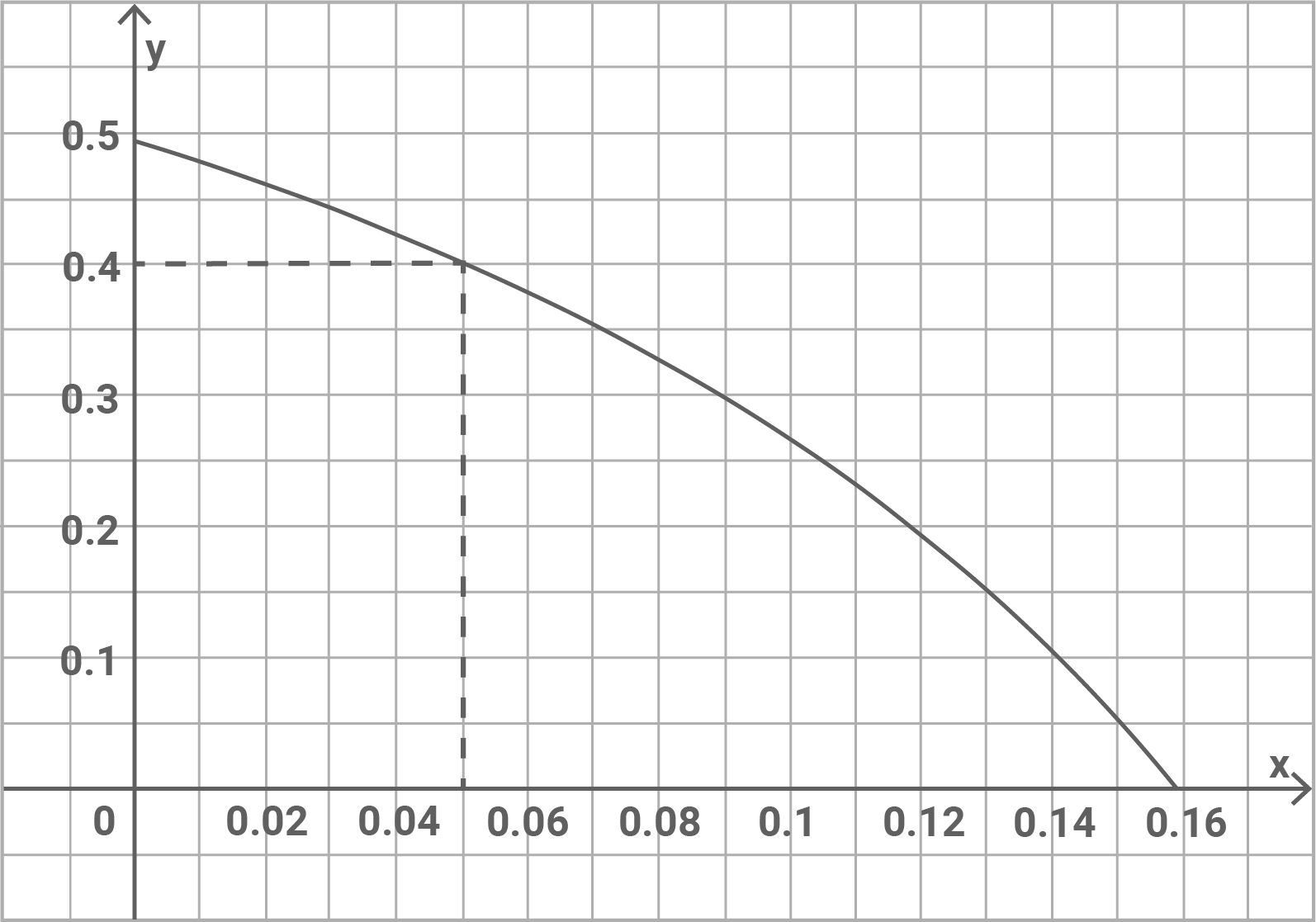
Der Wert, für den gilt, ist
Sachzusammenhang beschreiben
Der Anteil überbelegter Haushalte unter den Haushalten mit mindestens einem Kind ist um zurückgegangen. Gleichzeitig machen Haushalte mit mindestens einem Kind
aller überbelegten Haushalte aus.