Pflichtaufgabe 1 - Analysis

Pflichtaufgabe 1 - Analysis

Gegeben ist die Funktion $f$ in ihrem größtmöglichen Definitionsbereich durch

$y=f(x)=\mathrm{ln}(x+9)$ .

Ihr Graph sei $G$ .

a) Gib für die Funktion $f$ den größtmöglichen Definitionsbereich und den Wertebereich an und ermittle die Nullstelle.
Gib für den Graphen $G$ die Koordinaten des Schnittpunktes mit der $y$ -Achse sowie eine Gleichung seiner Asymptote an.

Beschreibe, wie der Graph $G$ aus dem Graphen der Funktionen $g$ mit
$g(x)=\mathrm{ln}\,x$ und $x\in \mathbb{R}$ , $x\gt 0$ , hervorgeht.
Schließe daraus, ob die Funktion $f$ lokale Extremstellen besitzt.

Zeichne den Graphen $G$ unter Einbeziehung der bisherigen Untersuchungsergebnisse.

b) Die Strecke $\overline{OP}$ mit $O(0\mid 0)$ und $P(-0,25\mid f(-0,25))$ , der Graph $G$ und die Abszissenachse schließen eine Fläche vollständig ein.
Zeige, dass die Funktion $F$ mit der Gleichung $F(x)=(x+9)\cdot \mathrm{ln}(x+9)-x$ eine Stammfunktion der Funktion $f$ ist und berechne die Maßzahl des Inhalts dieser Fläche.

c) Berechne diejenige Stelle, an der der Graph $G$ und der Graph der Funktion $h$ mit $h(x)=x^2$ den gleichen Anstieg haben.

d) Zeige, dass die Funktion $z$ mit $x\in \mathbb{R}$ und

$z(x)\begin{cases}x^2 \hspace{2.92cm} \text{für} \hspace{1cm} -\infty \lt x \leq0\\\mathrm{ln} (x+9) \hspace{1.53cm} \text{für} \hspace{1.1cm} 0\lt x \lt \infty\end{cases}$

an der Stelle $x=0$ nicht stetig ist.
Begründe, dass die Funktion $z$ an der Stelle $x=0$ auch nicht differenzierbar ist.

Aufgabe 1

a) $\blacktriangleright$ Größtmöglichen Definitionsbereich bestimmen

Hier ist die Funktion $f$ durch

$y=f(x)=\ln (x+9)$

gegeben. Deine Aufgabe ist es den größtmöglichen Definitionsbereich von $f$ zu bestimmen.

Der Definitionsbereich $\mathbb{D}$ gibt alle Werte an, die man in die Funktion einsetzen darf. Der natürliche Logarithmus ist allgemein nur für Zahlen echt größer Null definiert.

In diesem Fall ist die Funktion für alle $x$ definiert, für die gilt

$\begin{array}[t]{rll} x + 9 &>& 0\quad \scriptsize \mid\; -9\\[5pt] x &>& -9 \end{array}$

Der Definitionsbereich ist somit $\mathbb{D} = \{ x \in \mathbb{R}\;|\; x>-9 \}$ . Alternativ kann der Definitionsbereich auch so angegeben werden: $\mathbb{D}=]-9;\infty[$ .

$\blacktriangleright$ Wertebereich bestimmen

Der Wertebereich der natürlichen Logarithmusfunktion ist gesamt $\mathbb{R}$ .

Der Wertebereich ist deshalb $\mathbb{W}=\{\mathbb{R}\}$

$\blacktriangleright$ Nullstellen ermitteln

Nullstellen sind die Stellen, an denen der Funktionswert einer Funktion gleich Null ist. Um diese zu bestimmen, musst du den Funktionsterm mit Null gleichsetzen und nach $x$ auflösen.

$\begin{array}[t]{rll} f(x) &=& 0\\[5pt] \ln (x+9)&=& 0\quad \scriptsize \mid\; \mathrm e\\[5pt] \mathrm e^{\ln(x+9)}&=&\mathrm e^0\\[5pt] x+9 &=& 1\quad \scriptsize \mid\; -9\\[5pt] x &=& -8 \end{array}$

Die Funktion $f$ hat eine Nullstelle bei $x_N=-8$

$\blacktriangleright$ Schnittpunkt des Graphen $\boldsymbol{G}$ mit der $\boldsymbol{y}$ -Achse

Der Graph einer Funktion schneidet an der Stelle $x=0$ die $y$ -Achse. Wenn du die Koordinaten für den Schnittpunkt bestimmen willst, musst du $x=0$ in den Funktionsterm einsetzen.

$\begin{array}[t]{rll} f(0)&=& \ln(9)\\[5pt] f(0)&\approx& 2,1972 \end{array}$

Der Schnittpunkt mit der $y$ -Achse ist $S_y(0\,|\,\ln(9)\,)$ oder $S_y(0\,|\,2,1972)$ .

$\blacktriangleright$ Gleichung der Asymptote

Der natürliche Logarithmus strebt gegen $-\infty$ wenn der Term in Klammer gegen Null strebt. An dieser Stelle liegt eine senkrechte Asymptote vor.

Bei dieser Funktion geht $x+9 \rightarrow 0$ für $x \rightarrow -9$ . Die Asymptotengleichung ist $x=-9$

$\blacktriangleright$ Beschreiben des Graphen $\boldsymbol{G}$

Der Verlauf des Graphen $G$ entspricht dem Verlauf des Graphen der natürlichen Logarithmusfunktion $g$ mit $g(x)=\ln (x)$ . Der Unterschied liegt darin, dass der Graph $G$ gegenüber dem Graphen der Funktion $g$ um 9 Einheiten in Richtung der negativen $x$ -Achse verschoben ist. Da die Funktion $g$ keine lokalen Extremstellen hat, hat auch die Funktion $f$ keine lokalen Extremstellen.

$\blacktriangleright$ Zeichnen des Graphen $\boldsymbol{G}$

Der Graph hat die selbe Form wie der Graph der Funktion $\ln(x)$ , ist allerdings um 9 Einheiten in Richtung der negativen $x$ -Achse verschoben. Bei $x=-9$ besitzt er eine senkrechte Asymptote. Für $x$ -Werte, die kleiner als $-9$ sind, ist er nicht definiert. Die $x$ -Achse wird an der Stelle $x=-8$ geschnitten. Die $y$ -Achse wird bei $y=2,1972$ vom Graphen geschnitten. Der Anstieg des Graphen wird für $x \rightarrow -9$ maximal und nimmt im Verlauf mit steigenden $x$ -Werten weiter ab, bleibt allerdings stets positiv.

Diagramm mit Linien und Gitterstruktur, möglicherweise zur Datenvisualisierung oder Analyse.

b) $\blacktriangleright$ Zeige, dass $\boldsymbol{F}$ eine Stammfunktion von $\boldsymbol{f}$ ist

Die Funktion $F$ ist gegeben durch die Gleichung

$F(x)=(x+9)\cdot \ln(x+9)-x\text{.}$

Um zu zeigen, dass $F$ eine Stammfunktion von $f$ ist, musst du $F$ ableiten und überprüfen, ob der Funktionsterm der Ableitung mit dem Funktionsterm von $f$ übereinstimmen.

Zum Ableiten verwendest du hier die Produkt- und die Kettenregel

$\begin{array}[t]{rll} F‘(x)&=&1\cdot \ln(x+9) + (x+9)\cdot \dfrac{1}{x+9} - 1 \\[5pt] &=&\ln(x+9) + \dfrac{x+9}{x+9} -1 \\[5pt] &=&\ln(x+9) = f(x) \end{array}$

Du hast jetzt gezeigt, dass die Ableitung von $F$ gleich $f$ ist, somit ist $F$ eine Stammfunktion von $f$ .

$\blacktriangleright$ Maßzahl des Flächeninhalts

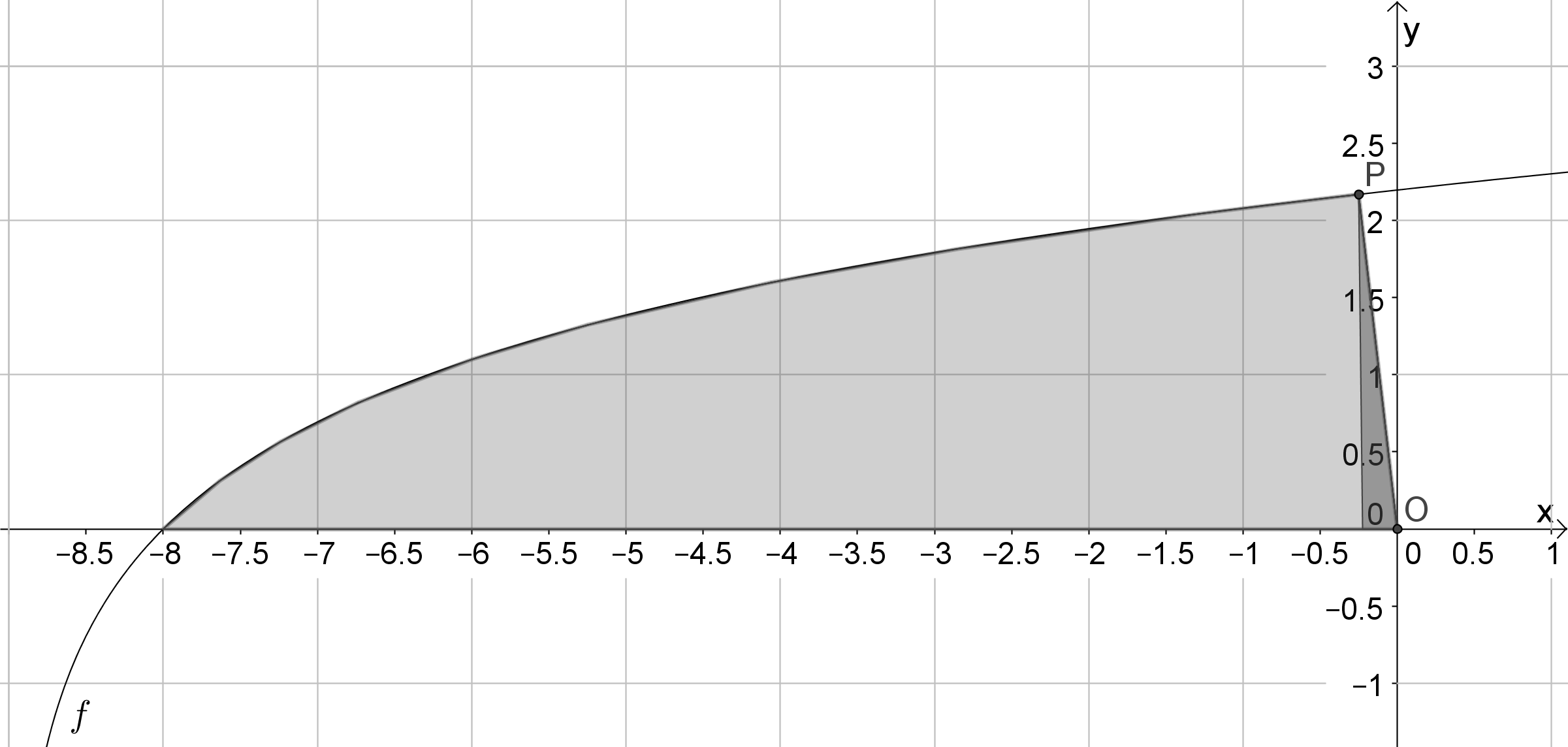
Hier sollst du den Flächeninhalt zwischen dem Graphen $G$ , der Strecke $\overline{OP}$ und der Abszissen-Achse, also der $x$ -Achse, bestimmen. Als erstes solltest du eine Skizze anfertigen, in der du die Fläche, deren Flächeninhalt du bestimmen willst, aufzeichnest. Wenn du dir die Skizze ansiehst, kannst du besser verstehen, um welche Fläche es sich handelt.

Diagramm mit einer grauen Fläche, die eine Funktion darstellt, auf einem Gitterhintergrund.

Um den Flächeninhalt zu bestimmen, teilst du die Fläche in zwei Teilabschnitte. Der erste Abschnitt beginnt an der Schnittstelle des Graphen mit der $x$ -Achse und endet an der Schnittstelle des Graphen von $f$ mit der Strecke $\overline{OP}$ . Der Flächeninhalt der Fläche lässt sich als Integral über die Funktion $f$ bestimmen.

Die zweite Teilfläche bildet die Fläche unter der Strecke $\overline{OP}$ . Da es sich bei der Fläche unter der Strecke $\overline{OP}$ um ein rechtwinkliges Dreieck handelt, kann die Fläche über die Höhe und Breite des Dreiecks bestimmt werden.

1. Schritt: Integral berechnen

Um das Integral zu berechnen, benötigst du eine Stammfunktion der Funktion $f$ . Du hast bereits gezeigt, dass $F$ eine Stammfunktion von $f$ ist, daher kannst du $F$ als Stammfunktion verwenden. Die Integrationsgrenzen sind die Schnittstelle des Graphen $G$ mit der $x$ -Achse bei $x_1=-8$ und die Schnittstelle des Graphen $G$ und der Strecke $\overline{OP}$ bei $x_2=-0,25$ .

$\begin{array}[t]{rll} A_{\text{int}} = \displaystyle\int_{-8}^{-0,25}\;\ln(x+9)\mathrm dx&=& F(-0,25)-F(-8)\\[5pt] &=&(-0,25+9)\cdot\ln(-0,25+9)-(-0,25)-((-8 +9)\cdot\ln(-8+9)-(-8))\\[5pt] &=&8,75\cdot\ln(8,75)-1\cdot\ln(1)-7,75\\[5pt] &=&8,75\cdot\ln(8.75)-7,75\\[5pt] &\approx&11,2292 \end{array}$

2. Schritt: Flächeninhalt des Dreiecks bestimmen

Bei der zweiten Teilfläche handelt es sich um ein rechtwinkliges Dreieck. Der Flächeninhalt eines solchen Dreiecks kannst du mit dieser Formel bestimmen:

$A_{\triangle}=\dfrac{1}{2}\cdot g \cdot h$

Die Grundseite $g$ geht von $x=-0,25$ bis $x=0$ , die Länge der Grundseite ist also $g=0,25$ . Die Höhe $h$ steht senkrecht auf der Grundseite, sie ist in durch den Funktionswert der Schnittstelle zwischen Graph und Strecke $\overline{OP}$ gegeben. Die Schnittstelle ist bei $x=-0,25$ , der Funktionswert ist

$\begin{array}[t]{rll} f(-0,25)&=&\ln(-0,25 + 9) \approx 2,1691\text{.}\\[5pt] \end{array}$

Die Fläche des Dreiecks ist also:

$\begin{array}[t]{rll} A_{\triangle}&\approx& \dfrac{1}{2}\cdot 0,25 \cdot 2,169 \\[5pt] &\approx& 0,2711 \end{array}$

3. Schritt: Summe bilden

Abschließend musst du die beiden Flächeninhalte addieren, um auf ein Endergebnis zu kommen.

$\begin{array}[t]{rll} A_{\text{ges}}&=& A_{\text{int}} + A_{\triangle} \\[5pt] &=& 11,2292 + 0,2711 \\[5pt] &=& 11,5003 \\[5pt] \end{array}$

Die Maßzahl ist in etwa 11,5 FE.

c) $\blacktriangleright$ Stellen gleicher Steigung der Graphen von $\boldsymbol{h}$ und $\boldsymbol{f}$ bestimmen

Die Steigung eines Graphen ist immer durch die erste Ableitung der Funktion gegeben. Die Stellen, an denen beide Graphen die gleiche Steigung haben, sollst du bestimmen. Dazu musst du beide Funktionen einmal ableiten, gleichsetzen und nach $x$ auflösen.

1. Schritt: Ableitungen bilden

Die Ableitung von $f$ bildest du mit der Kettenregel, die Ableitung von $h$ mit der Potenzregel.

$\begin{array}[t]{rll} f(x) &=& \ln(x+9)\\[5pt] f‘(x)&=&\dfrac{1}{x+9}\\[5pt] \end{array}$

$\begin{array}[t]{rll} h(x)&=&x^2\\[5pt] h‘(x)&=&2x\\[5pt] \end{array}$

2. Schritt: $\boldsymbol{x}$ -Stellen bestimmen

$\begin{array}[t]{rll} f‘(x) &=& h‘(x) \\[5pt] \dfrac{1}{x+9}&=& 2x&\quad& \scriptsize \mid\; \cdot(x+9)\\[5pt] 1&=&2x^2+18x &\quad& \scriptsize \mid\; -1\\[5pt] 0 &=& 2x^2 + 18x -1 \\[5pt] \end{array}$

Um die Gleichung zu lösen, gibt es zwei Möglichkeiten. Du verwendest entweder die Mitternachtsformel oder die pq-Formel.

Mitternachtsformel:

$\begin{array}[t]{rll} 0 &=& 2x^2 + 18x -1 \\[5pt] x_{1/2}&=& \dfrac{-b \pm \sqrt{b^2-4ac}}{2a} \\[5pt] &=&\dfrac{-18 \pm \sqrt{324 + 8}}{4} \\[5pt] &=&\dfrac{-18 \pm \sqrt{332}}{4} \\[5pt] x_1 &=& 0,0552 \\[5pt] x_2 &=& -9,0552 \\[5pt] \end{array}$

pq-Formel:

$\begin{array}[t]{rll} 0 &=& x^2+9x -0,5\\[5pt] x_{1/2}&=&-\dfrac{p}{2}\pm \sqrt{(\dfrac{p}{2})^2-q}\\[5pt] &=& -4,5 \pm \sqrt{4,5^2-(-0,5)}\\[5pt] &=& -4,5 \pm \sqrt{20,75}\\[5pt] x_1 &=& 0,0552 \\[5pt] x_2 &=& -9,0552 \\[5pt] \end{array}$

Die Stellen, an denen die Graphen der Funktionen $g$ und $h$ den selben Anstieg haben, sind $x_1=0,0552$ und $x_2=-9,0552$ .

d) $\blacktriangleright$ Zeige, dass $\boldsymbol{z}$ an der Stelle $\boldsymbol{x=0}$ nicht stetig ist

$z(x)$ ist gegeben durch:

$\begin{array}[t]{rll} z(x)=\begin{cases}x^2&\text{für } -\infty \lt x \le 0 \\ \ln(x+9)&\text{für } 0 \lt x \lt \infty \end{cases} \\[5pt] \end{array}$

Um zu zeigen, dass eine beliebige Funktion $z$ an einer Stelle $x_0$ stetig ist, muss an der Stelle $x_0$ eine Bedingung erfüllt sein.

$z(x_0^+)=z(x_0^-)$

Wobei $z(x_0^+)$ bedeutet, dass man sich von der positiven $x$ -Richtung an die Stelle $x_0$ nähert. $z(x_0^-)$ bedeutet dementsprechend, dass man sich von der negativen $x$ -Richtung an die Stelle $x_0$ nähert. Zusammenfassend willst du also zeigen oder widerlegen, dass der Funktionswert an der Stelle $x_0$ gleich bleibt, egal aus welcher Richtung man sich der Stelle nähert.
Um zu zeigen, dass $z$ bei $x=0$ nicht stetig ist, zeigst du, dass die Stetigkeitsbedingung nicht erfüllt ist. Dazu überprüfst du, ob die Funktionswerte übereinstimmen, wenn man sich von der negativen $x$ -Richtung, also x \lt x $_0$ , an x $_0$ und von der positiven $x$ -Richtung, also x \gt x $_0$ , an x $_0$ nähert.

$\begin{array}[t]{rll} z(x_0^+)&=&z(x_0^-) \\[5pt] 0^2&\neq&\ln(0+9) \\[5pt] 0 &\neq& \ln(9) \\[5pt] \end{array}$

Die Werte stimmen nicht überein, somit ist die Funktion $z$ an der Stelle $x=0$ nicht stetig.

$\blacktriangleright$ Zeige, dass $\boldsymbol{z}$ an der Stelle $\boldsymbol{x=0}$ nicht differenzierbar ist

Eine Funktion $z$ ist an einer Stelle $x_0$ differenzierbar, wenn diese Bedingung erfüllt ist:

$z‘(x_0^+)=z(‘x_0^-)$

Das bedeutet, dass die Ableitung an der Stelle $x_0$ übereinstimmen muss, egal ob du dich von der positiven oder negativen $x$ -Richtung näherst.

1. Schritt: Ableiten

Um zu zeigen, dass die Bedingung nicht erfüllt ist, leitest du die Funktion $z$ zunächst ab:

$\begin{array}[t]{rll} z‘(x)=\begin{cases}2x&\text{für } -\infty \lt x \le 0\\ \dfrac{1}{x+9}&\text{für } 0 \lt x \lt \infty \end{cases} \\[5pt] \end{array}$

2. Schritt: $\boldsymbol{x=0}$ einsetzen

Im nächsten Schritt musst du die Stelle, an der du die Differenzierbarkeit überprüfen willst, in die Ableitung einsetzen und überprüfen, ob der Wert der Ableitung an dieser Stelle aus beiden Richtungen übereinstimmt. Hier ist die gesuchte Stelle bei $x=0$ .

$\begin{array}[t]{rll} z‘(x_0^+)&=&z‘(x_0^-) \\[5pt] 2\cdot 0 &\neq& \dfrac{1}{0+9} \\[5pt] 0 &\neq& \dfrac{1}{9} \\[5pt] \end{array}$

Du siehst, dass sich der Ableitungswert unterscheidet wenn man sich von positiver und negativer $x$ -Richtung an die Stelle $x=0$ nähert. Somit ist die Funktion $z$ an der Stelle $x=0$ nicht differenzierbar.