Wahlpflichtaufgaben (Aufgabengruppe 2)

5.1

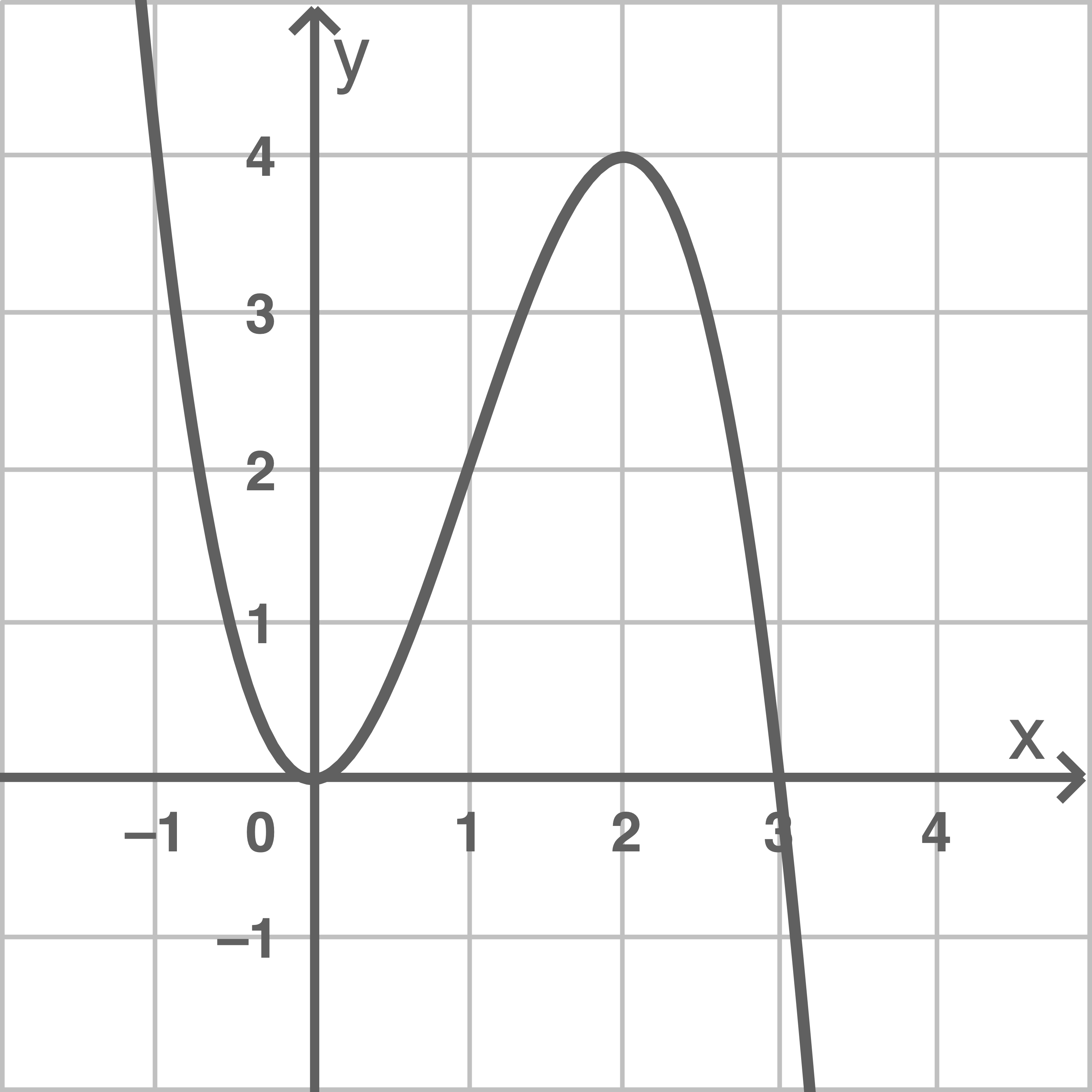
Die Abbildung zeigt den Graphen einer in $\mathbb{R}$ definierten Funktion $f.$

Es gilt: $\(f$

Abbildung

Deute die Aussage $\(f$ geometrisch.

(1 BE)

Begründe die folgende Aussage.

Für jede Stelle $x_0$ des Intervalls $[0;2]$ nimmt das Produkt aus lokaler Änderungsrate von $f$ an der Stelle $x_0$ und mittlerer Änderungsrate von $f$ im Intervall $[0;2]$ höchstens den Wert $6$ an.

(4 BE)

5.2

Die Grundfläche eines geraden Kreiskegels liegt in der $xy$ -Ebene und wird durch einen Kreis mit dem Radius $9$ begrenzt. Der Punkt $S\left( 0\mid 0 \mid 6\right)$ beschreibt die Spitze des Kreiskegels.

Die Gerade mit dem Richtungsvektor $\pmatrix {3\\4\\-6}$ , die $S$ enthält, schneidet die $xy$ -Ebene im Punkt $P.$
Bestimme das Verhältnis der Längen der Strecken, in die $P$ den Durchmesser des Kreises teilt.

(5 BE)

5.3

In einem Behälter befinden sich eine schwarze Kugel und $w$ weiße Kugeln, wobei $w \geq 2.$ Für ein Spiel wird aus dem Behälter zweimal nacheinander eine Kugel ohne Zurücklegen zufällig entnommen.

Gib unter der Annahme, dass $w=3$ ist, die Wahrscheinlichkeit dafür an, dass die schwarze Kugel im ersten Zug entnommen wird.

(1 BE)

Der Einsatz bei diesem Spiel beträgt $2 \,\text{€}.$ Wird die schwarze Kugel beim ersten Zug entnommen, werden $8 \,\text{€}$ ausgezahlt, wird sie beim zweiten Zug entnommen, so beträgt die Auszahlung $4 \,\text{€}.$ Wird bei keinem der beiden Züge die schwarze Kugel entnommen, erfolgt keine Auszahlung. Bei wiederholter Durchführung des Spiels ist zu erwarten, dass sich auf lange Sicht Einsätze und Auszahlungen ausgleichen. Ermittle den zugehörigen Wert von $w.$

(4 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

5.1

An der Stelle $x=1$ hat der Graph von $f$ die Steigung $3.$

Mittlere Änderungsrate im Intervall $\left[ 0; 2\right]: \dfrac{f(2)-f(0)}{2-0}=2$

Im Intervall $\left[0 ; 2\right]$ besitzt der Graph nur an der Stelle $x=1$ einen Wendepunkt. Dort erreicht die Steigung des Graphen im Punkt $(1 \mid f(1))$ ihren größten Wert. Da $f^{\prime}(1)=3$ gilt, folgt für jede Stelle $x_0$ im betrachteten Intervall: $\(2 \cdot f$

5.2

Die Gerade durch $S(0 \mid 0 \mid 6)$ mit Richtungsvektor $\pmatrix{3\\4\\-6}$ hat die Gleichung:

$\overrightarrow{x}(t) = \pmatrix{0\\0\\6} + t \cdot \pmatrix{3\\4\\-6} = \pmatrix{3t\\4t\\6-6t}$

Die Gerade schneidet die $xy$ -Ebene bei $z=0.$

Aus der dritten Zeile folgt somit:

$\begin{array}[t]{rlll} 6-6t &=& 0 &\mid\; -6 \\[5pt] -6t &=& -6 &\mid\; :(-6) \\[5pt] t &=& 1 \end{array}$

Einsetzen in die Geradengleichung ergibt: $\overrightarrow{OP} = \pmatrix{3\\4\\0}$

Die Strecke vom Mittelpunkt der Grundfläche des Zylinders $O(0\mid 0 \mid 0)$ zu $P$ hat die Länge:

$|\overrightarrow{OP}| = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5$

Der Kreis hat den Radius $9,$ also ist der Durchmesser $18.$

Der Punkt $P$ teilt den Durchmesser in zwei Teilstrecken:

Die eine Teilstrecke ist gegeben durch die Länge des Radius plus des Abstands von $P$ zum Mittelpunkt $O,$ das heißt $9+5=14.$

Die andere Teilstrecke ist gegeben durch die Länge des Durchmessers minus die erste Teilstrecke, das heißt $18-14=4.$

Somit ist das Verhältnis der zwei Teilstrecken $14:4$ bzw. $7:2.$

5.3

$p=\dfrac{1}{4}$

Es befinden sich $w$ weiße und eine schwarze Kugel in der Urne. Der Einsatz beträgt $2 \: \text{€}.$

Wird die schwarze Kugel im ersten Zug gezogen, beträgt die Auszahlung $8 \: \text{€}:$

Wahrscheinlichkeit: $\dfrac{1}{w+1}$

Wird die schwarze Kugel im zweiten Zug gezogen (nachdem zuerst eine weiße gezogen wurde), beträgt die Auszahlung $4\: \text{€}:$

Wahrscheinlichkeit: $\dfrac{w}{w+1} \cdot \dfrac{1}{w}$

Es ergibt sich folgende Gleichung für den Erwartungswert:

$\begin{array}[t]{rll} 8 \cdot \dfrac{1}{w+1} + 4 \cdot \dfrac{w}{w+1} \cdot \dfrac{1}{w} &=& 2 \\[5pt] 8 \cdot \dfrac{1}{w+1} + 4 \cdot \dfrac{1}{w+1} &=& 2 \\[5pt] 12 \cdot \dfrac{1}{w+1} &=& 2 &\mid\; \cdot (w+1) \\[5pt] 12 &=& 2w+2 &\mid\; -2 \\[5pt] 10 &=& 2w &\mid\; :2 \\[5pt] w &=& 5 \end{array}$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?