Aufgabe 3.2: Stochastik
Ein Unternehmen bietet Joghurt in Bechern an. Die Becher werden auf Paletten mit jeweils
Gegenwärtig wird für jeden Becher eines der sechs Motive zufällig ausgewählt. Drei Becher werden nacheinander geöffnet.
a)
Berechne die Wahrscheinlichkeit dafür, dass sich nur im ersten und dritten Becher jeweils das Motiv 
befindet.
(2 BE)
b)
Gib im Sachzusammenhang ein Ereignis an, dessen Wahrscheinlichkeit durch den Term 
angegeben wird.
(2 BE)
Das Unternehmen plant eine Änderung. Künftig soll für jeden Becher das Motiv
c)
Die Abbildung zeigt für einen Wert von 
die Wahrscheinlichkeitverteilung von 
.
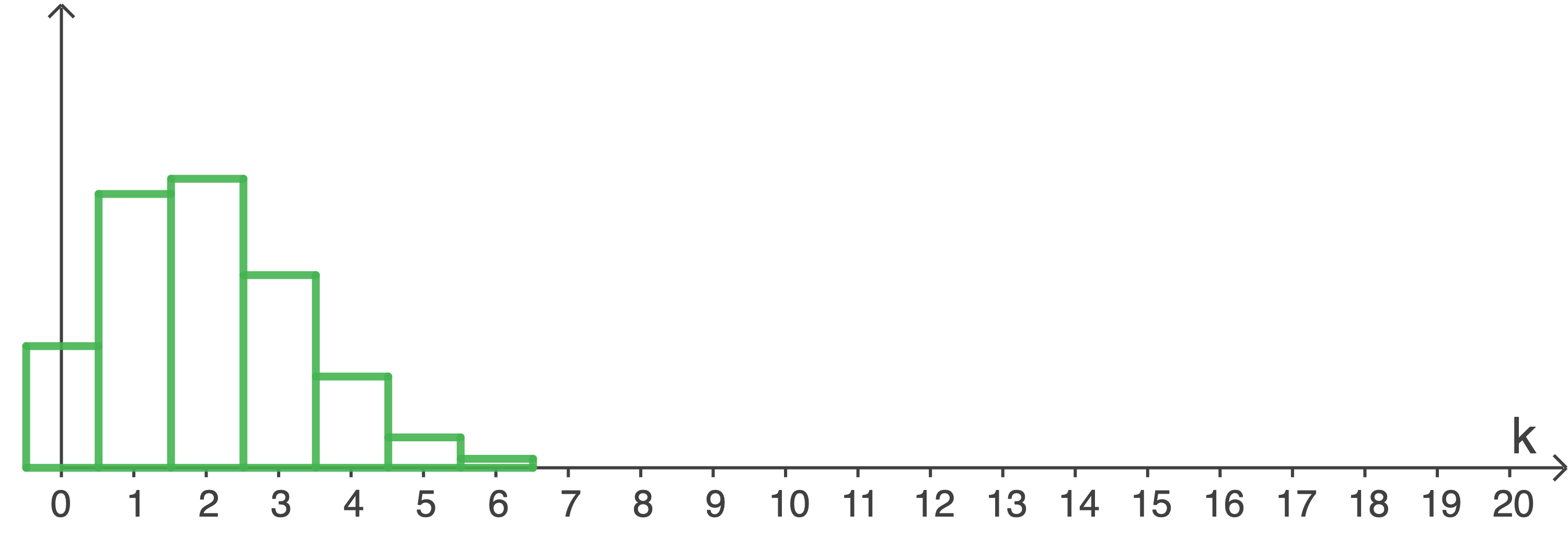Beurteile jede der beiden folgenden Aussagen:
I.
Die Wahrscheinlichkeit dafür, dass sich auf einer Palette weniger als zwei Becher mit dem Motiv 
befinden, ist größer als 
.
II.
Der Wert von ist größer als 
(4 BE)
Nach der Änderung wird für jeden Becher das Motiv
d)
Gib jeweils einen Wert von 
und 
an, sodass mit dem Term 
die Wahrscheinlichkeit eines Ereignisses im Sachzusammenhang berechnet werden kann. Beschreibe das zugehörige Ereignis.
(4 BE)
e)
Kunden können für gesammelte Motive Prämien gewinnen. Der Tabelle können die Kosten entnommen werden, die dem Unternehmen dadurch entstehen.
Berechne die mittleren Kosten pro Becher, die dem Unternehmen durch die Prämien entstehen.
| Motiv | Wahrscheinlichkeit für die Auswahl | Kosten pro Becher |
|---|---|---|
| 1 | 4 Cent | |
| 2 | 4 Cent | |
| 3 | 2 Cent | |
| 4 | 2 Cent | |
| 5 | 2 Cent | |
| 6 | 9 Cent |
(4 BE)
f)
Bei einem Fünftel aller Becher ist das Motiv farbig gedruckt, bei den anderen Bechern schwarz-weiß. Die Wahrscheinlichkeit dafür, dass sich in einem zufällig ausgewählten Becher mit einem schwarz-weiß gedruckten Motiv das Motiv befindet, beträgt 
Berechne die Wahrscheinlichkeit dafür, dass ein zufällig ausgewählter Becher mit einem farbigen Motiv das Motiv enthält.
(4 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
Mit der Pfadmultiplikationsregel ergibt sich:
Mit einer Wahrscheinlichkeit von ca. 2 % befindet sich das Motiv 1 jeweils nur im ersten und im dritten Becher.
b)
In allen drei Bechern befindet sich jeweils ein anderes Motiv.
c)
1)
Die Aussage I ist falsch, da der Anteil des Flächeninhalts der beiden Säulen zu 
am Flächeninhalt aller dargestellten Säulen nicht größer als 
ist.
2)
Die Aussage II ist falsch, da für 
wegen 
die Säule zu 
nicht die höchste wäre.
d)
Der Term 
beschreibt die Wahrscheinlichkeit dafür, dass sich unter 
Bechern kein einziger mit dem Motiv 6 befindet.
Analog dazu sollte der übrige Teil des Gesamtterms die Wahrscheinlichkeit dafür darstellen, dass sich unter Bechern genau einmal das Motiv 6 befindet.
Es gilt daher
und 
Auf einer Palette befinden sich 20 Becher. Ein Ereignis lautet:
Auf zwei Paletten befindet sich höchstens ein Becher, der das Motiv 6 enthält.
Analog dazu sollte der übrige Teil des Gesamtterms die Wahrscheinlichkeit dafür darstellen, dass sich unter
Es gilt daher
e)
Die jeweilige Wahrscheinlichkeit für die Motive 1 bis 5 beträgt 
Pro Becher entstehen dem Unternehmen dadurch im Mittel ca. 3 ct Kosten.
f)
Mit wird die gesuchte Wahrscheinlichkeit bezeichnet. Mit den Pfadregeln ergibt sich dann:
![\(\begin{array}[t]{rll}
\frac{1}{5}\cdot p + \frac{4}{5}\cdot \frac{1}{48} &=& \frac{1}{36} \\[5pt]
\frac{1}{5}\cdot p + \frac{1}{60} &=& \frac{1}{36} &\quad \scriptsize \mid\;- \frac{1}{60} \\[5pt]
\frac{1}{5}\cdot p &=& \frac{1}{90}&\quad \scriptsize \mid\;\cdot 5 \\[5pt]
p &=& \frac{1}{18}
\end{array}\)](https://mathjax.schullv.de/1c047af8fecc93c06ed84ce887e2cb94178ad3c5e06d5ce52a5ad5a0598e9f17?color=5a5a5a)
Die Wahrscheinlichkeit dafür, dass ein zufällig ausgewählter Becher mit einem farbigen Motiv das Motiv 6 enthält, beträgt 