Aufgabe 1 - Analysis

1.1

Betrachtet werden die in $\mathbb{R}$ definierten Funktionen $f_k$ mit
$f_k(x)=-kx\cdot(x-8),$ $k \in\mathbb{R},$ $k\gt0.$ Der Graph von $f_k$ wird mit $G_k$ bezeichnet.

$\,$

Gib die Nullstellen von $f_k$ an.

(2 BE)

$\,$

Begründe, dass der Punkt $(4\mid 16k)$ der Hochpunkt von $G_k$ ist.

(3 BE)

$\,$

Bestimme den Abstand der Hochpunkte von $G_k$ und $G_{k+1}.$

(2 BE)

$\,$

Berechne denjenigen Wert von $k$ , für den der Inhalt der Fläche, die $G_k$ mit der $x$ -Achse einschließt, $\dfrac{64}{3}$ beträgt.

(4 BE)

$\,$

Gib die Stellen an, an der jede Stammfunktion von $f_{\frac{1}{4}}$ ihr Maximum annimmt.
Begründe die Angabe ohne Verwendung eines Terms einer Stammfunktion.

(3 BE)

$\,$

Die Abbildung zeigt den Graphen von $f_{\frac{1}{4}}.$ Betrachtet werden die Trapeze mit den Eckpunkten $A(0\mid0),$ $B(8\mid0),$ $C_u(8-u\mid f_{\frac{1}{4}}(u))$ und $D_u(u\mid f_{\frac{1}{4}}(u))$ , wobei $u$ alle Werte des Intervalls $0\lt u \lt 4$ annimmt.

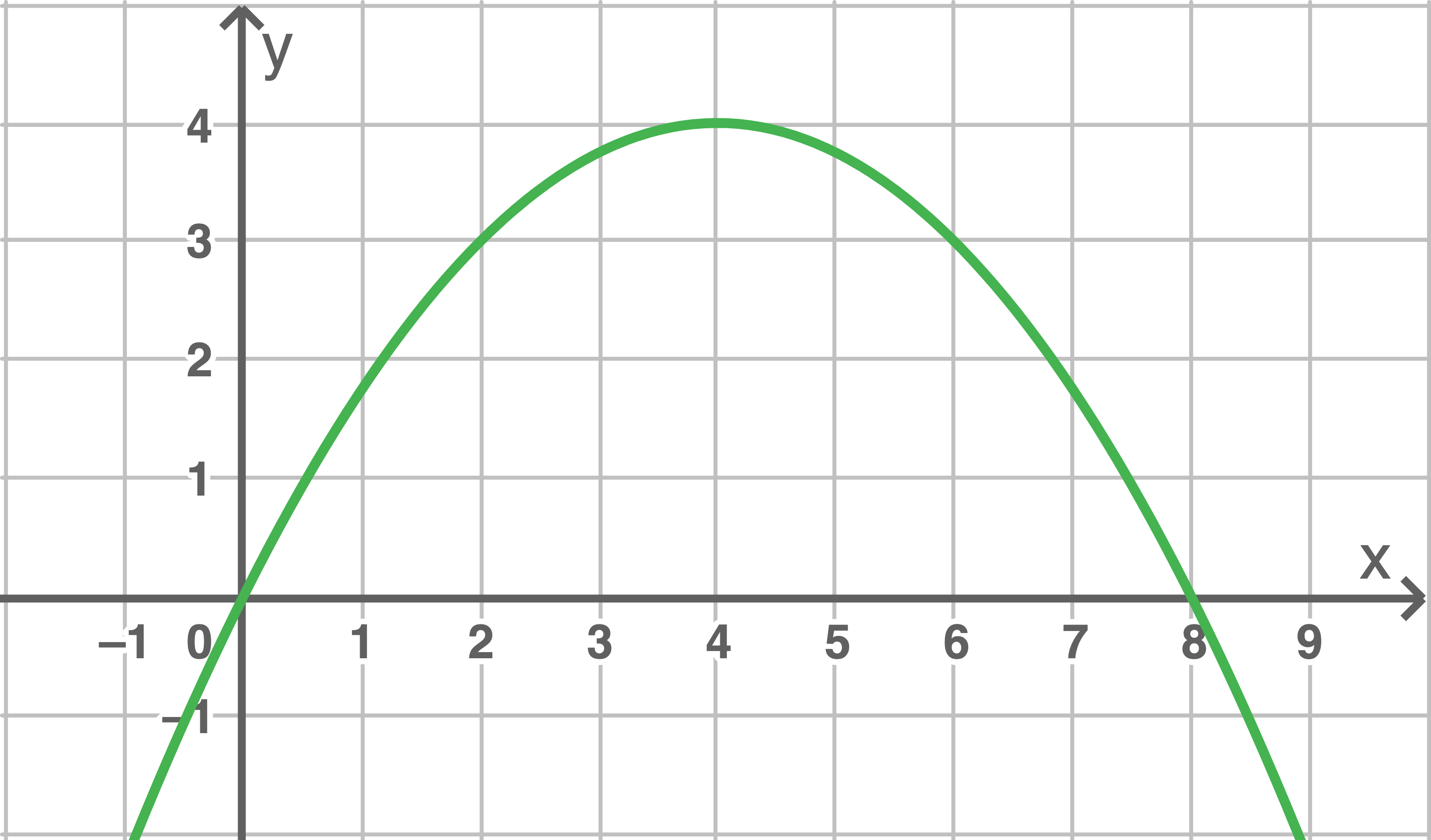
sachsen anhalt abi ga 2019 aufgabe 1 analysis abbildung 1 funktion fk

$\,$

Zeichne das Trapez für $u=1$ in die Abbildung ein.

(2 BE)

$\,$

Gib einen Term an, mit dem die Länge der beiden gleich langen Schenkel des Trapezes $ABC_uD_u$ berechnnet werden kann.

(2 BE)

$\,$

Der Flächeninhalt des Trapezes $ABC_uD_u$ kann mit dem Term $(8-u)\cdot f_\frac{1}{4}(u)$ berechnet werden. Beschreibe eine geometrische Überlegung, mit der sich dieser Term herleiten lässt.

(4 BE)

1.2

In einem Raum wurde die Wirksamkeit der Lüftungsanlage untersucht. Dazu wurde die Konzentration des Kohlenstoffdioxids $(CO_2)$ in der Luft gemessen, während sich eine Personengruppe im Raum befand. Die Messwerte können mithilfe der in $\mathbb{R}$ definierten Funktion $g$ mit $g(x)=-600\mathrm{e}^{-0,5x}+1000$ beschrieben werden.
Dabei ist $x$ die seit Beginn der Untersuchung vergangene Zeit in Stunden und $g(x)$ die $CO_2$ -Konzentration in „parts per million“ (kurz: ppm).

$\,$

Einer Studie zufolge fühlen sich Personen in Räumen wohl, wenn die $CO_2$ -Konzentration geringer als $1000 \,\text{ppm}$ ist. Untersuche, ob diese Bedingung während der Untersuchung erfüllt war.

(2 BE)

$\,$

Stelle die zeitliche Entwicklung der $CO_2$ -Konzentration für die ersten zehn Stunden nach Beginn der Untersuchung grafisch dar.

(2 BE)

$\,$

Zeige, dass die mittlere Änderungsrate der $CO_2$ -Konzentration für jede Zeitspanne mit einer Länge von einer Stunde mithilfe des Terms $600 \cdot \left(1-\dfrac{1}{\sqrt{\mathrm{e}}}\right)\cdot \mathrm{e}^{-0,5x}$ bestimmt werden kann. Berechne denjenigen Zeitpunkt auf eine Minute genau, für den die beschriebene mittlere Änderungsrate erstmals den Wert $100\dfrac{\text{ppm}}{\text{h}}$ unterschreitet.

(4 BE)

1.1

Die Nullstellen von $f_k$ ergeben sich mit dem Satz vom Nullprodukt zu $x_1 = 0$ und $x_2 = 8.$

$\,$

Bei $f_k$ handelt es sich um eine ganzrationale Funktion zweiten Grades. Der zugehörige Graph ist eine achsensymmetrische Parabel. Die Symmetriachse verläuft parallel zur $y$ -Achse durch den Scheitelpunkt der Parabel. Wegen $k\gt0$ und dem negativen Vorzeichen handelt es sich um eine nach unten geöffnete Parabel. Der Scheitelpunkt ist also ein Hochpunkt.
Die Nullstellen von $f_k$ sind $x_1=0$ und $x_2=8.$ Aufgrund der Symmetrie muss der Hochpunkt daher an der Stelle $x_H = \dfrac{x_2 -x_1}{2}= 4$ liegen.
Die zugehörige $y$ -Koordinate ist:

$f_k(4)=16k$

Vollständige Lösung anzeigen

$\,$

Die $x$ -Koordinate des Hochpunkts aller Funktionen $G_k$ ist identisch. Der Abstand ergibt sich also lediglich über die $y$ -Koordinate:

$16(k+1) - 16k = 16$

Der Abstand der Hochpunkte von $G_k$ und $G_{k+1}$ beträgt $16\,LE.$

$\,$

$k= \frac{1}{4}$

Vollständige Lösung anzeigen

Für $k=\frac{1}{4}$ beträgt der Inhalt der von $G_k$ mit der $x$ -Achse eingeschlossenen Fläche $\frac{64}{3}.$

$\,$

Wenn $F_{\frac{1}{4}}$ eine Stammfunktion von $f_{\frac{1}{4}}$ ist, so ist $F_{\frac{1}{4}}‘= f_{\frac{1}{4}}.$
Eine Maximalstelle von $F_{\frac{1}{4}}$ liegt genau an der Stelle vor, an der ihre erste Ableitungsfunktion eine Nullstelle mit Vorzeichenwechsel von positiv zu negativ besitzt.
$f_{\frac{1}{4}}$ besitzt eine solche Nullstelle bei $x=8.$

Jede Stammfunktion von $f_{\frac{1}{4}}$ nimmt ihr Maximum also an der Stelle $x=8$ an.

$\,$

Diagramm einer Parabel mit Punkten A, B, C und D auf einem Koordinatensystem.

Abb. 1: Trapez $ABC_1D_1$

$\,$

$l_u=\sqrt{u^2 + (f_{\frac{1}{4}}(u))^2}$

Vollständige Lösung anzeigen

$\,$

Die längere der beiden parallelen Seiten des Trapezes ist $8\,\text{LE}$ lang. Die Länge der kürzeren der beiden parallelen Seiten ist:

$(8-u)-u = 8-2u$

Der Mittelwert dieser beiden Seitenlängen ist $\dfrac{8+8-2u}{2} = 8-u.$

Die die Grundseite des Trapezes auf der $x$ -Achse liegt, ist die Höhe des Trapezes $f_{\frac{1}{4}}(u).$ Für den Flächeninhalt werden dann der Mittelwert der parallelen Seiten und die Höhe des Trapezes multipliziert.

1.2

Es ist $-600\mathrm e^{-0,5x} \lt 0$ für alle $x\in \mathbb{R}.$ Der Funktionsterm von $g$ ist daher so aufgebaut, dass vom Summanden $1000$ für alle $x\in\mathbb{R}$ etwas subtrahiert wird. $g(x)$ ist also in jedem Fall kleiner als $1000.$ Die Bedingung war daher während der Untersuchung erfüllt.