Pflichtaufgaben
Die Abbildung zeigt den Graphen der in definierten Funktion
Der Graph von
wird mit
bezeichnet.
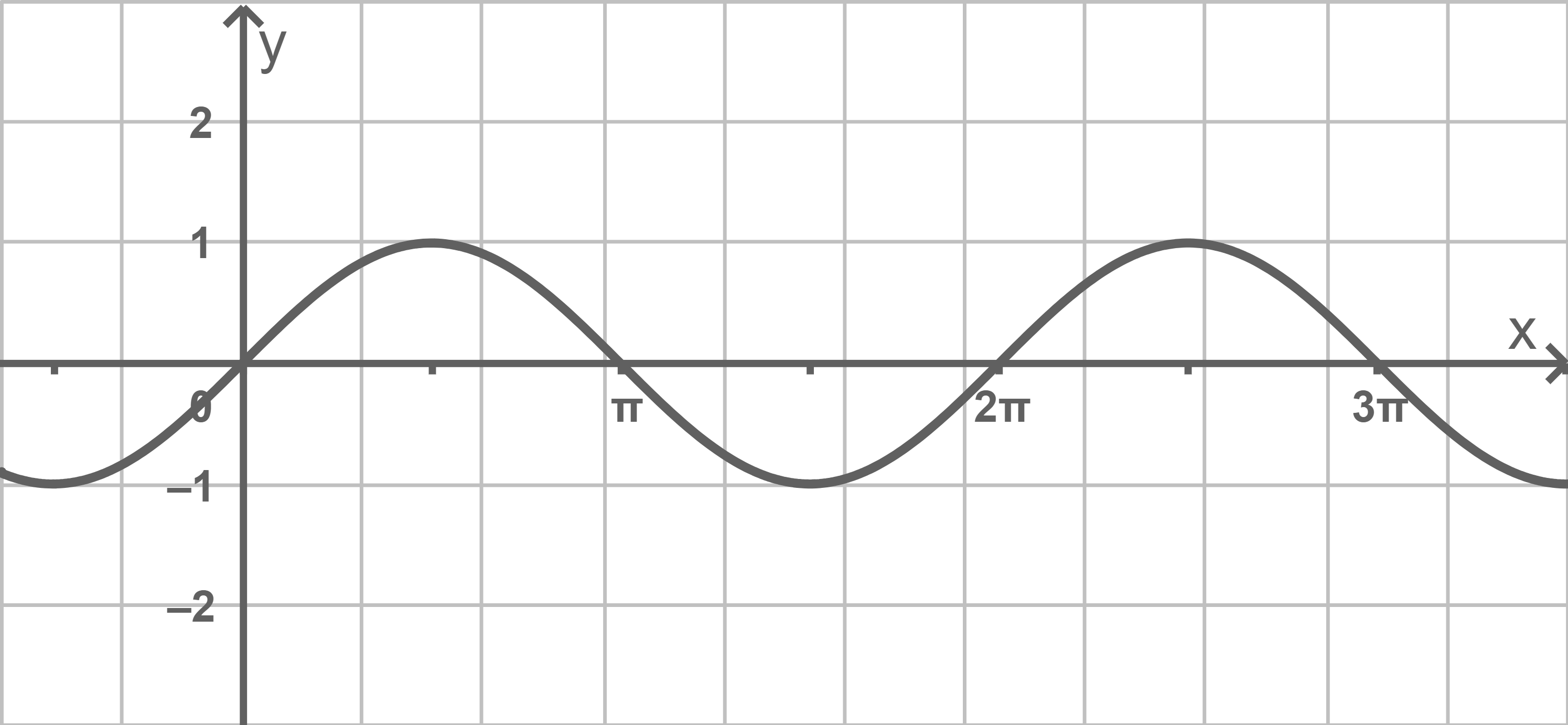
Gib den Wertebereich von an.
Gib die Koordinaten eines Wendepunkts von an.
Der Graph einer Funktion kann aus
erzeugt werden, indem
- um
in positive
-Richtung verschoben und
- mit dem Faktor
in
-Richtung gestreckt wird.
Skizziere in der Abbildung den Graphen von
Gegeben sind die Gerade durch die Punkte
und
sowie die Gerade
mit
Berechne die Koordinaten des Schnittpunkts von und
Die Geraden und
liegen in der Ebene
Gib eine Gleichung einer Ebene an, die parallel zu
verläuft und den Koordinatenursprung enthält. Begründe deine Angabe.
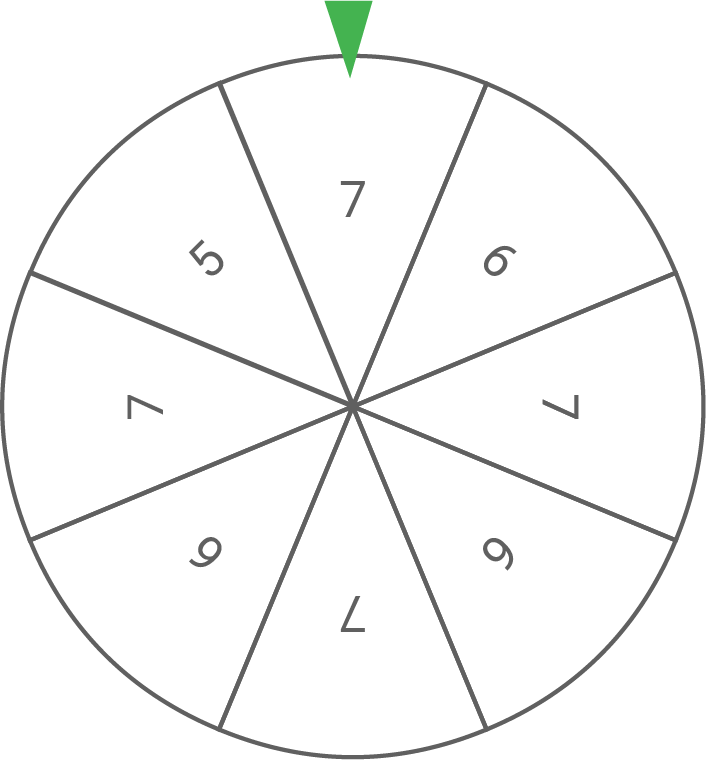
Interpretiere den Term im Sachzusammenhang.
Berechne die Wahrscheinlichkeit dafür, dass die Summe der erzielten Zahlen ungerade ist.
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?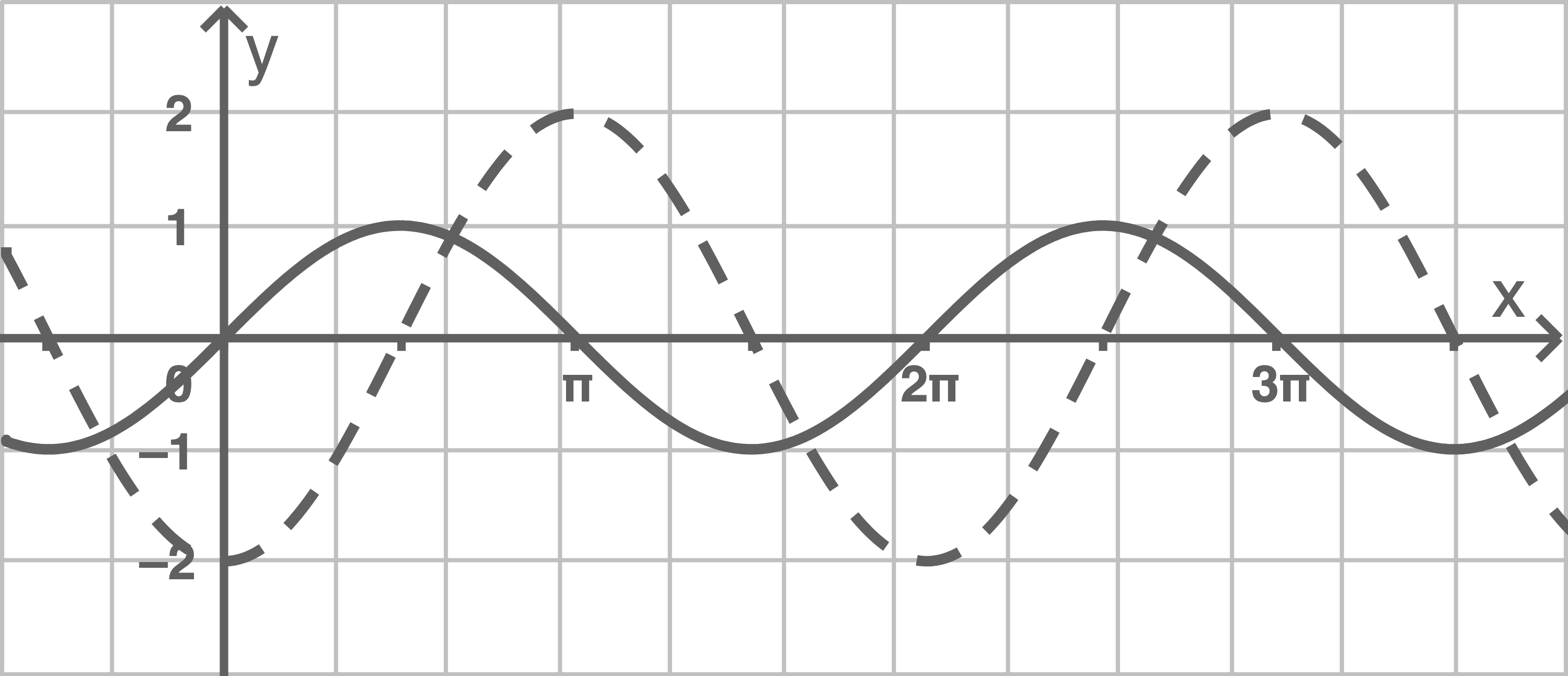
Geradengleichung für aufstellen
Geraden und
gleichsetzen
Aus der zweiten Zeile folgt:
Schnittpunkt bestimmen
Der Schnittpunkt zwischen den Geraden
und
hat die Koordinaten
Ebenengleichung angeben
Angabe begründen
Die Ebenen und
liegen parallel, weil sie den gleichen Normalenvektor besitzen. Einsetzen des Koordinatenursprungs in
liefert
somit enthält
diesen.
Der Term gibt die Wahrscheinlichkeit dafür an, dass bei zweimaligem Drehen des Glücksrads zweimal die Zahl erzielt wird.
Die Summe ist dann ungerade, wenn zweimal gedreht wird und die Zahl einmal gerade und einmal ungerade ist.