Aufgabe 1: Analysis

1.1

Abbildung 1 zeigt den Graphen $G_{f}$ der in $\mathbb{R}$ definierten Funktion $f_a: x \mapsto \frac{1}{3} x^3-2 x+4.$

$G_{f}$ ist symmetrisch bezüglich des Punkts $(0 \mid 4).$

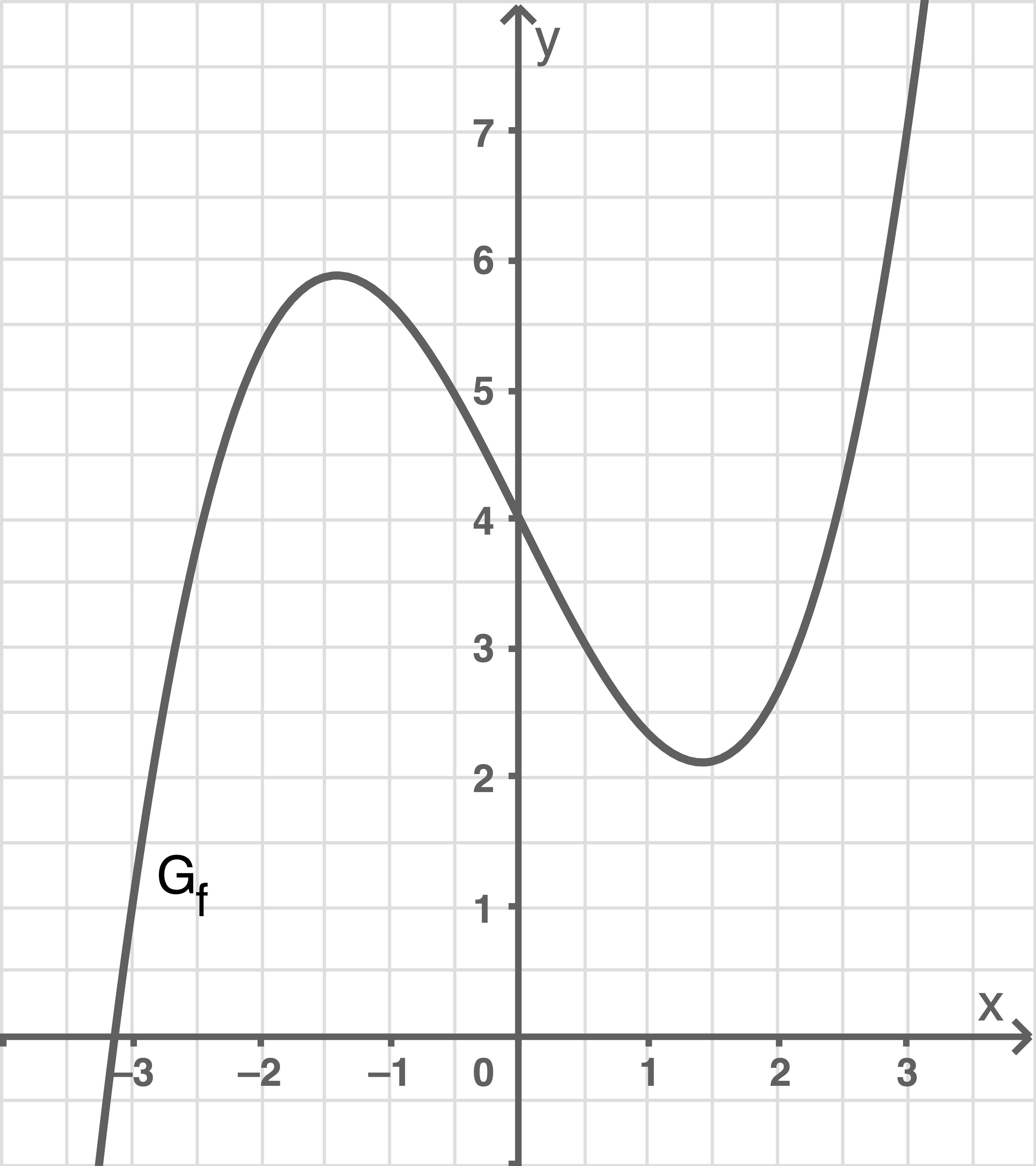
Abbildung

Abbildung 1

Berechne die Extremstellen von $f$ und gib das Monotonieverhalten von $f$ an.

(4 BE)

Die Tangente an $G_{f}$ im Punkt $P (3 \mid f(3))$ wird mit $t$ bezeichnet.

Bestimme rechnerisch eine Gleichung von $t.$ Zeichne den Punkt $P$ und die Tangente $t$ in Abbildung 1 ein.

[Ergebnis zur Kontrolle: $t: y=7x-14$ ]

(5 BE)

Es gilt für alle $x \in \mathbb{R}: f(x)-(7x-14) = \frac{1}{3} \cdot (x-3)^2 \cdot (x+6)$

Begründe mithilfe dieses Zusammenhangs, dass $t$ und $G_f$ neben $P$ genau einen weiteren gemeinsamen Punkt besitzen.

(3 BE)

Betrachtet wird die Gleichung $\displaystyle\int_{k}^{k+1}f(x)\;\mathrm dx = 4$ mit $k \in \mathbb{R}.$

Es gibt eine Zahl $k$ mit $-1,5 \leq k \leq 1,5,$ die eine Lösung dieser Gleichung ist. Gib – ohne weitere Rechnung – diese Zahl an und begründe deine Angabe mithilfe geeigneter Eintragungen in Abbildung 1.

(5 BE)

1.2

Die Länge einer Fahrstrecke, die ein Elektroauto mit vollständig geladener Batterie ohne erneutes Aufladen unter bestimmten Bedingungen zurücklegen kann, wird als Nennreichweite des Elektroautos bezeichnet und ist für jedes Elektroauto ein fester Wert. Die tatsächliche Reichweite hängt von vielen Faktoren ab; im Folgenden wird ausschließlich die Abhängigkeit von der Außentemperatur betrachtet.

Diese Abhängigkeit kann für eine Vielzahl von Elektroautos modellhaft im Intervall $[-12;36]$ durch eine Funktion $r$ beschrieben werden. Dabei ist $x$ die Außentemperatur in $^{\circ}\mathrm{C}$ und $r(x)$ der Quotient aus der tatsächlichen Reichweite eines Elektroautos und dessen Nennreichweite. Abbildung 2 zeigt den Graphen der Funktion $r.$

Hat also $r$ beispielsweise für eine bestimmte Außentemperatur den Wert $0,6,$ so beträgt die tatsächliche Reichweite eines Elektroautos bei dieser Außentemperatur $60\,\%$ seiner Nennreichweite.

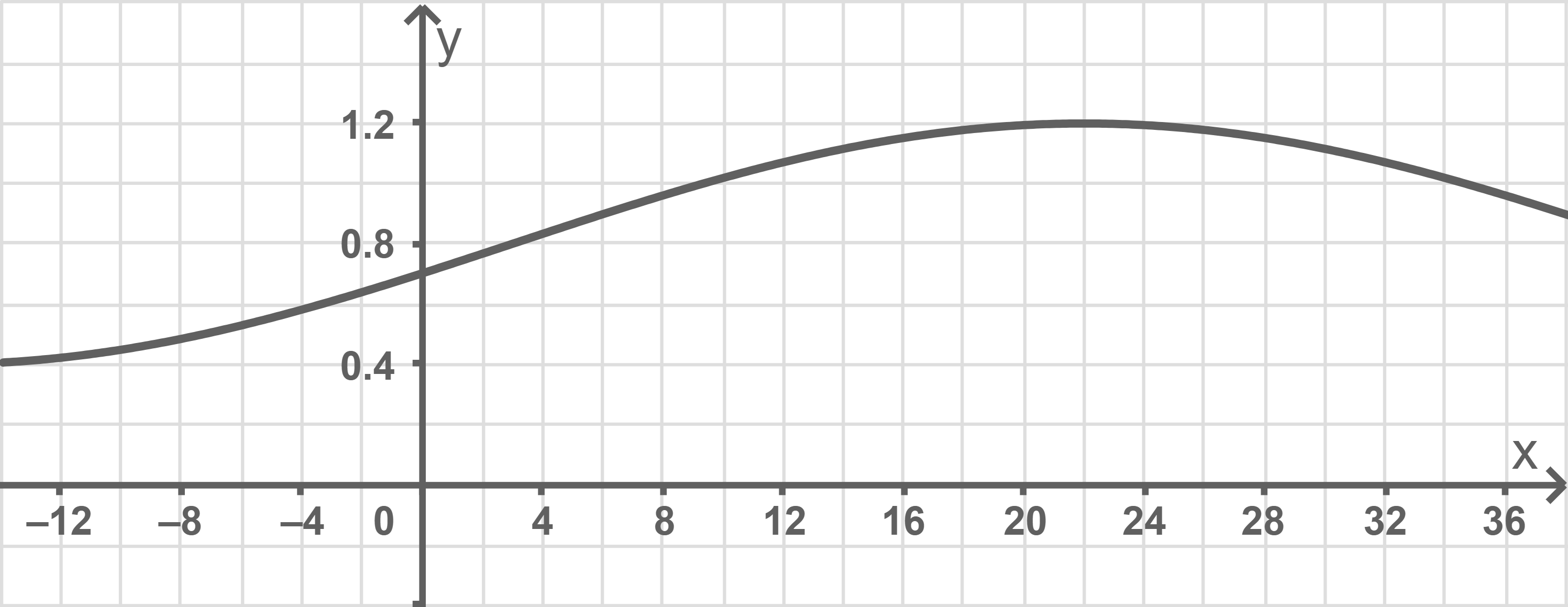
Abbildung 2

Im Folgenden werden nur Temperaturen im Bereich von $-12\;^{\circ} \mathrm{C}$ bis $36\;^{\circ}\mathrm{C}$ sowie Elektroautos betrachtet, bei denen der durch die Funktion $r$ beschriebene Zusammenhang gilt.

Gib anhand von Abbildung 2 die Koordinaten des Hochpunkts des Graphen von $r$ an.
Beschreibe die Bedeutung des Hochpunkts und seiner Koordinaten im Sachzusammenhang.

(4 BE)

Es gibt Außentemperaturen, bei denen die tatsächliche Reichweite eines Elektroautos größer ist als seine Nennreichweite.

Bestimme mithilfe von Abbildung 2 den entsprechenden Temperaturbereich.

(4 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1

1. Ableitung aufstellen

$\(f$

Mit der notwendigen Bedingung für Extremstellen folgt:

$\(\begin{array}[t]{rlll} f$

Extremstellen bei $x_1 = -\sqrt{2}$ und $x_2 = \sqrt{2}$

Monotonieverhalten bestimmen

monoton zunehmend für $x \leq -\sqrt{2}$ und $x \geq \sqrt{2}$
monoton abnehmend für $-\sqrt{2} \leq x \leq \sqrt{2}$

Tangentengleichung von $\boldsymbol{t}$ bestimmen

Steigung an der Stelle $x=3$ berechnen

$\(m=f$

$y$ -Koordinate der Stelle $x=3$ berechnen

$y=f(3) = 7$

Tangentengleichung aufstellen und ausgerechnete Werte für $m$ und $y$ einsetzen

$\begin{array}[t]{rlll} y &=& mx + n \\[5pt] 7 &=& 7 \cdot 3 + n &\mid\: -21 \\[5pt] n &=& -14 \end{array}$

Somit folgt für die Gleichung der Tangenten: $t: y = 7x - 14$

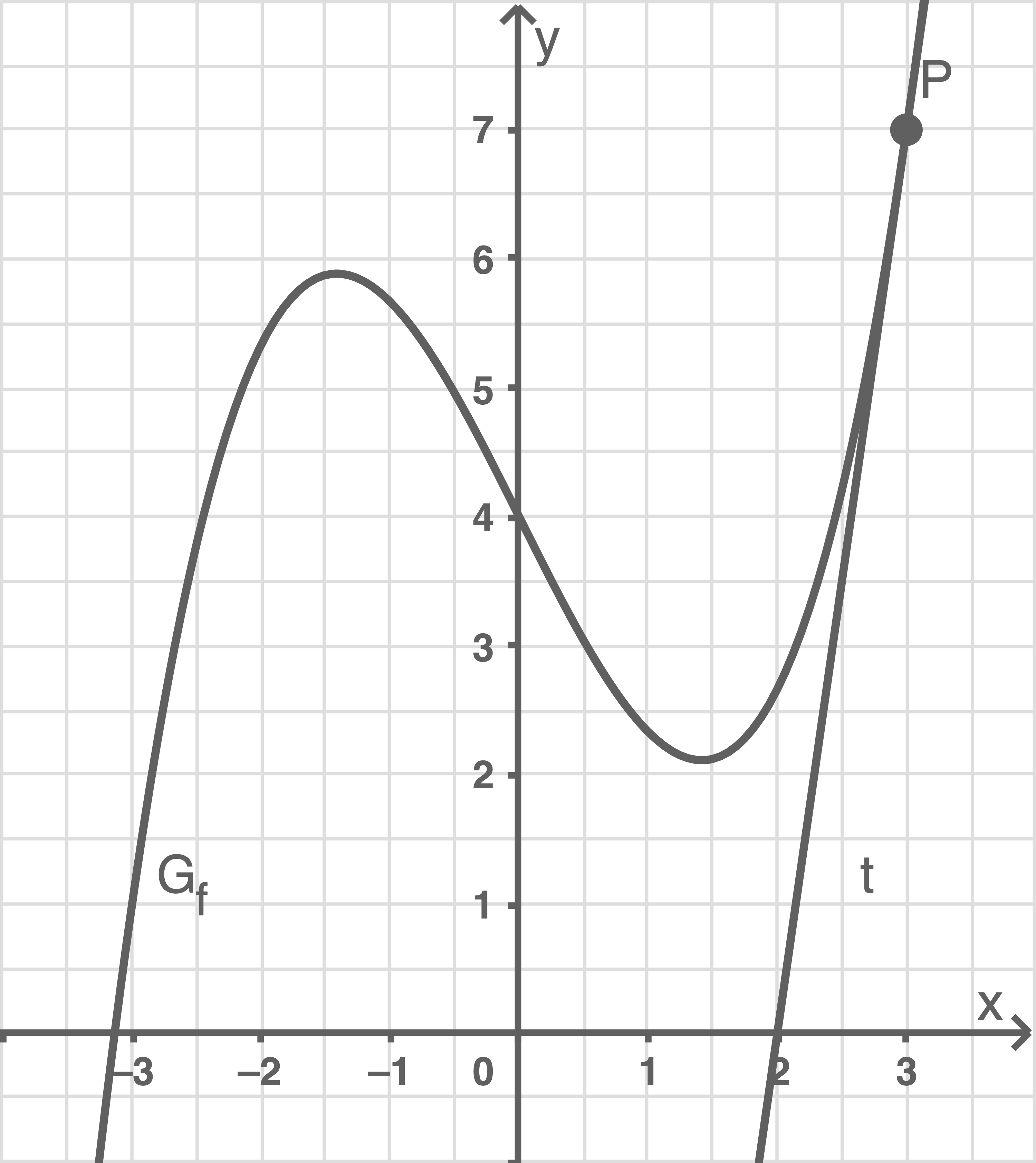
Den Punkt $\boldsymbol{P}$ und die Gerade $\boldsymbol{t}$ in die Abbildung einzeichnen

Rechenweg anzeigen

$f(x)-(7x-14) = \dfrac{1}{3}\cdot(x-3)^2\cdot(x+6)$

Damit gilt die Gleichheit aus der Aufgabenstellung. Der Graph $G_f$ und $t$ besitzen nur an den Stellen $x=3$ und $x=-6$ gemeinsame Punkte, denn für diese Werte wird die rechte Seite der Gleichung nach dem Satz des Nullprodukts Null und somit auch die linke Seite $f(x)-t(x).$ Da die $x$ -Koordinate von $P$ durch $x=3$ gegeben ist, existiert somit genau ein weiterer gemeinsamer Punkt.

$k = -\dfrac{1}{2}$

Durch geeignete Eintragungen sieht die Abbildung 1 folgendermaßen aus:

Aufgrund der Symmetrie von $G_f$ haben die beiden schraffierten Flächen den gleichen Inhalt; daher entspricht der Wert des folgenden Integrals dem Inhalt der Fläche eines Rechtecks der Länge $4$ und der Breite $1:$

$\displaystyle\int_{-\frac{1}{2}}^{\frac{1}{2}}f(x)\;\mathrm dx$

1.2

$(22 \mid 1,2)$

Die größte tatsächliche Reichweite liegt bei einer Außentemperatur von $22 \;^\circ\text{C}$ vor. Diese beträgt das $1,2$ -Fache der Nennreichweite.

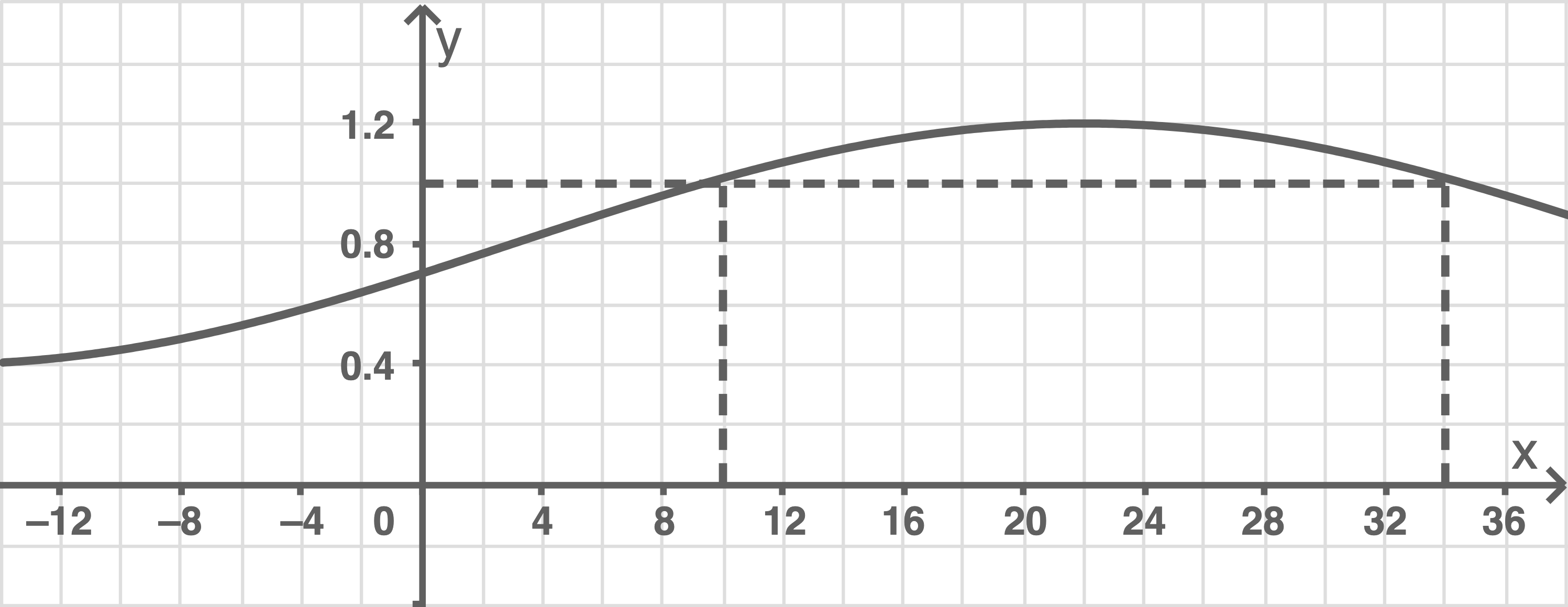
Der gesuchte Temperaturbereich erstreckt sich von etwa $10 \:^\circ\text{C}$ bis etwa $34 \:^\circ\text{C}$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?