Pflichtaufgabe 2 - Analytische Geometrie
Pflichtaufgabe 2 - Analytische Geometrie
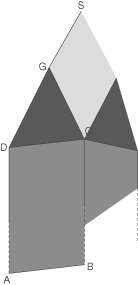 Die Eckpunkte einer Seite des Kirchturms seien mit
Die Eckpunkte einer Seite des Kirchturms seien mit  ,
,  ,
,  und
und  sowie
sowie  als Giebelspitze beschrieben.
als Giebelspitze beschrieben.
 beschrieben. Von ihr ausgehend werden Spannseile bis zum Erdboden geführt, die auf den Kanten des Daches liegen. Die Spannseile können als Seitenkanten einer vierseitigen, aus der
beschrieben. Von ihr ausgehend werden Spannseile bis zum Erdboden geführt, die auf den Kanten des Daches liegen. Die Spannseile können als Seitenkanten einer vierseitigen, aus der  -Ebene stehenden Spannseil-Pyramide aufgefasst werden.
-Ebene stehenden Spannseil-Pyramide aufgefasst werden.
Ein Kirchturm mit einem quaderförmigen Baukörper und quadratischer Grundfläche (Seitenlänge  ) soll restauriert werden. Die auf den Baukörper aufgesetzten Giebelwände haben die Form gleichschenkliger Dreiecke und sind jeweils
) soll restauriert werden. Die auf den Baukörper aufgesetzten Giebelwände haben die Form gleichschenkliger Dreiecke und sind jeweils  hoch. Jede der viereckigen Dachflächen ist eben.
hoch. Jede der viereckigen Dachflächen ist eben.
Die Beschreibung des Kirchturms erfolgt in einem dreidimensionalen kartesischen Koordinatensystem (eine Einheit entspricht einem Meter, die Horizontalebene entspricht der -Ebene).
-Ebene).
Der Koordinatenursprung markiert die Lage des Mittelpunktes der Grundfläche des Baukörpers und die Seiten der Grundfläche verlaufen parallel zur - bzw.
- bzw.  -Achse.
-Achse.
Die Beschreibung des Kirchturms erfolgt in einem dreidimensionalen kartesischen Koordinatensystem (eine Einheit entspricht einem Meter, die Horizontalebene entspricht der
Der Koordinatenursprung markiert die Lage des Mittelpunktes der Grundfläche des Baukörpers und die Seiten der Grundfläche verlaufen parallel zur

a) Gib die Koordinaten der Punkte  und
und  sowie die Höhe des quaderförmigen Baukörpers an.
sowie die Höhe des quaderförmigen Baukörpers an.
Die Spitze des Kirchturmdaches wird durch den Punkt
b) Die Gerade  beschreibt die Lage eines der Spannseile.
Gib eine Gleichung der Geraden
beschreibt die Lage eines der Spannseile.
Gib eine Gleichung der Geraden  an und berechne das Gradmaß des Winkels, den die Gerade
an und berechne das Gradmaß des Winkels, den die Gerade  mit der
mit der  -Achse einschließt.
Berechne sowohl die Koordinaten des Ankerpunktes eines solchen Spannseils als auch die Länge eines Spannseils.
-Achse einschließt.
Berechne sowohl die Koordinaten des Ankerpunktes eines solchen Spannseils als auch die Länge eines Spannseils.
c) Die nichtmaßstäblichen Abbildungen zeigen Grundrisse von Pyramiden; die grauen Quadrate veranschaulichen den Grundriss des Baukörpers.
Genau eine der beiden Abbildungen zeigt die Lage der Spannseil-Pyramide bezüglich des Baukörpers. Gib an und begründe, welche dies ist.
Genau eine der beiden Abbildungen zeigt die Lage der Spannseil-Pyramide bezüglich des Baukörpers. Gib an und begründe, welche dies ist.
Abb.1 

Abb.2 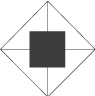

Aufgabe 2
Kirchturm
Bei dieser Aufgabe geht es um einen Kirchturm, der durch die Angabe verschiedener Informationen beschrieben wird. Die Kirche besteht aus einem quaderförmigen Baukörper, auf dem mit Giebelwänden ein Dach aufgebaut ist. Alle gegebenen Punkte liegen in einem kartesischen Koordinatensystem. Die
a) Bestimme die Koordinaten der Punkte
Bestimme die Koordinaten der Punkte  und
und 
Die Punkte
b) Gerade
Gerade 
Der höchste Punkt der Kirche ist die Dachspitze
c) Zeige, welche Abbildung passend ist
Zeige, welche Abbildung passend ist
Die Abbildungen zeigen eine Ansicht des Kirchturms von oben. Das schwarze Quadrat ist somit die Grundfläche des Baukörpers. Die Spannseile sind von der Dachspitze über die Giebelspitzen zum Boden gespannt. Da sich sie Giebelspitzen jeweils in der Mitte einer Seitenfläche befinden, erkennst du, dass Abb. 2 die Lage der Spannseil-Pyramide richtig darstellt. In Abb. 1 sind die Spannseile über die Ecken des Baukörpers gespannt, was nicht der Beschreibung in der Aufgabe entspricht.