Aufgabe 3
Ein Blatt DIN-A4-Papier liegt in der x -x
-x -Ebene. Gegeben sind seine Eckpunkte
-Ebene. Gegeben sind seine Eckpunkte  sowie der Punkt
sowie der Punkt  .1
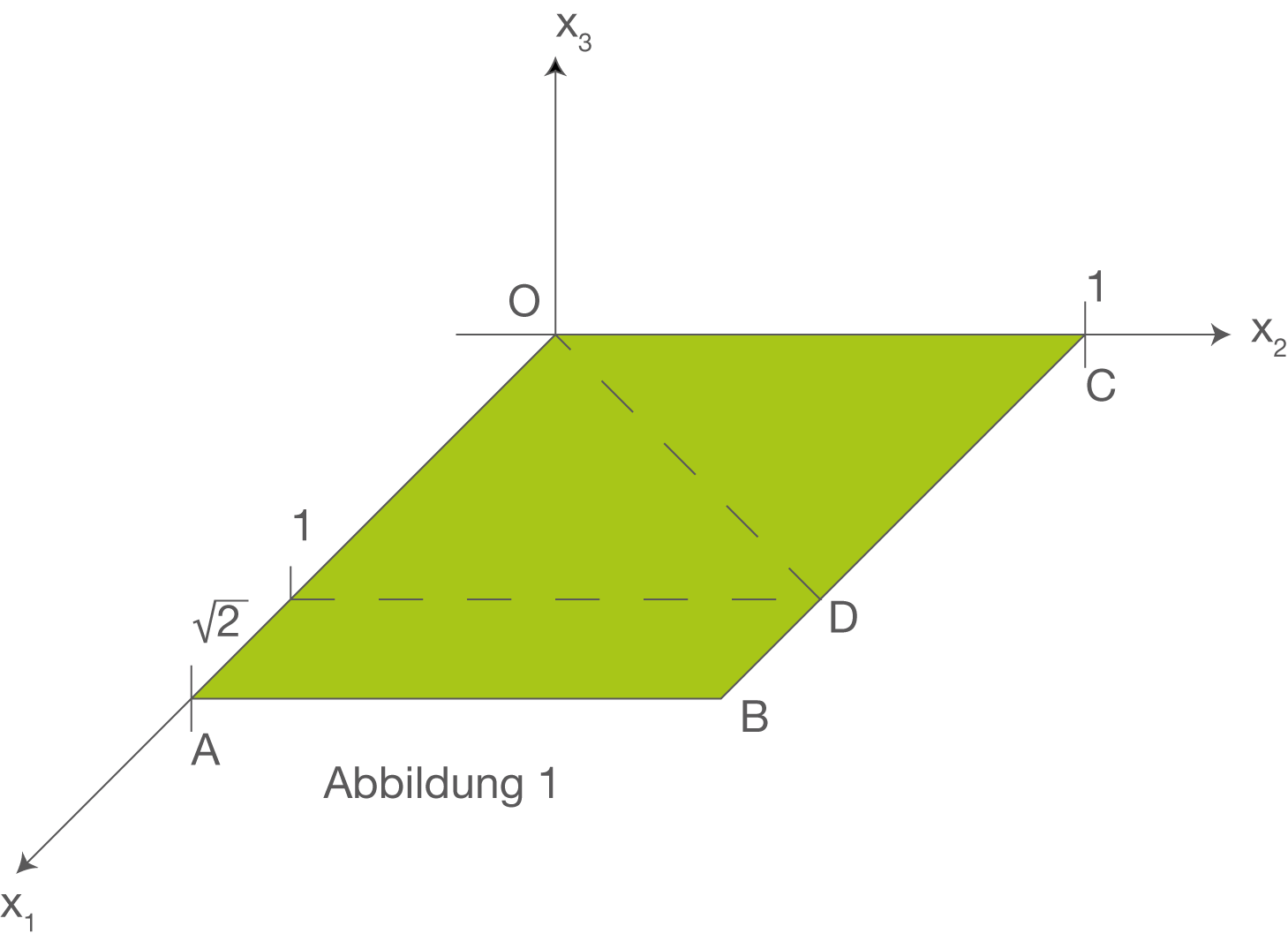
Das Blatt wird jetzt entlang der Strecke
.1
Das Blatt wird jetzt entlang der Strecke  gefaltet. Das Dreieck
gefaltet. Das Dreieck  bleibt dabei fest, während das Viereck
bleibt dabei fest, während das Viereck  in das Viereck
in das Viereck  übergeht, das wieder in der
übergeht, das wieder in der  Ebene liegt. Die Gegebenheiten sind in den folgenden Schrägbildern dargestellt.
Zur Veranschaulichung kann ein DIN-A4-Blatt entsprechend gefaltet werden.
Ebene liegt. Die Gegebenheiten sind in den folgenden Schrägbildern dargestellt.
Zur Veranschaulichung kann ein DIN-A4-Blatt entsprechend gefaltet werden.
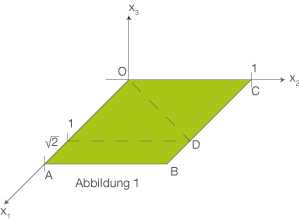
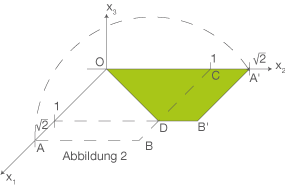


1 Als Längeneinheit (LE) wird die Länge der kürzeren Seite des DIN-A4-Blattes verwendet.
a)
- Geben Sie die Koordinaten des Mittelpunktes
der Strecke
an.
- Zeigen Sie, dass die Gerade
senkrecht zur Geraden
ist.
- Bestimmen Sie den Abstand des Punktes
von der Geraden
.
(3P + 5P + 4P)
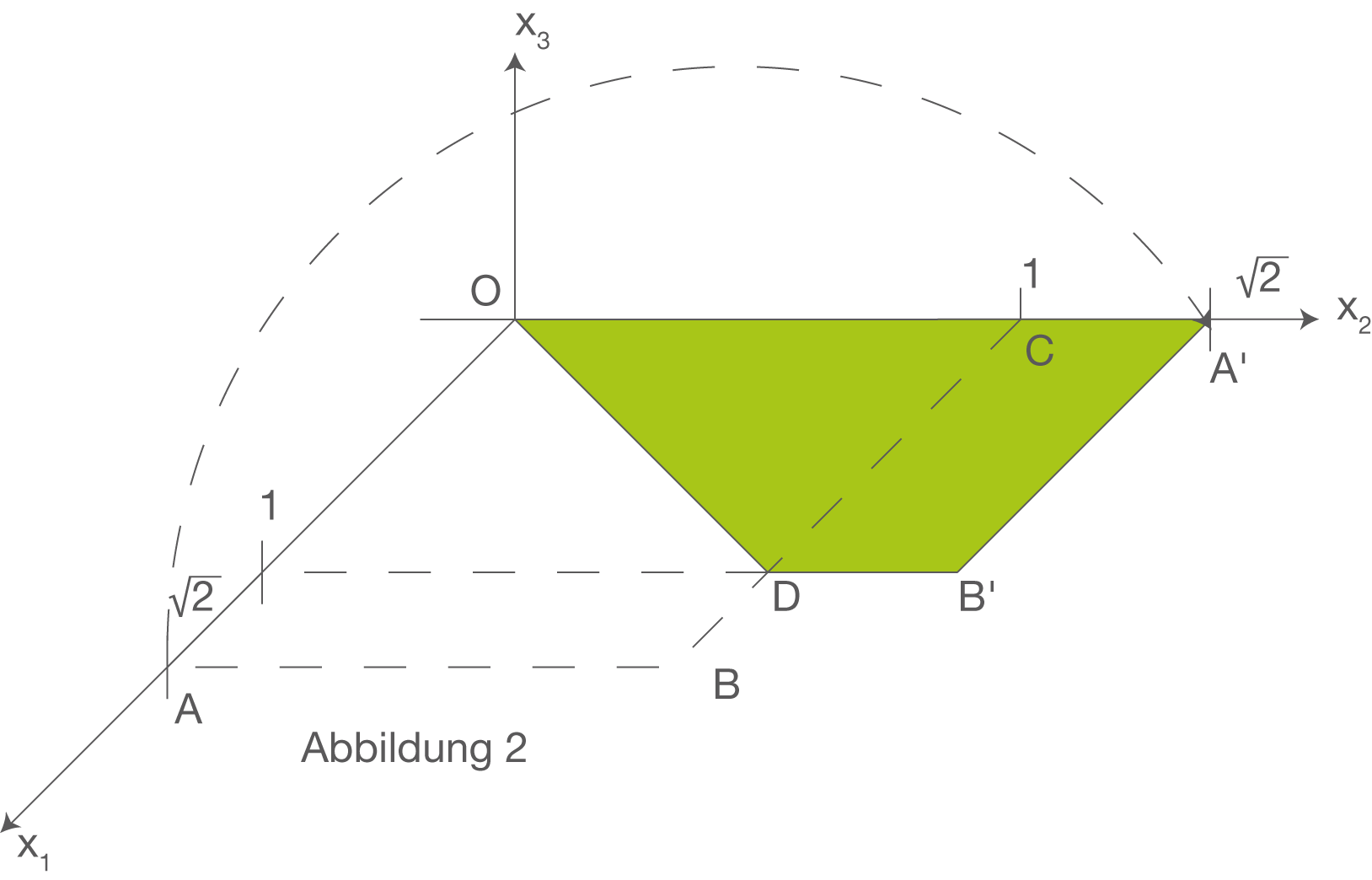
b) Die Ecke des Blattes, die durch das Falten aus der Position A in die Position A‘ gebracht wird, bewegt sich bei dem Faltvorgang auf einem Halbkreis in einer Ebene E, die senkrecht zur  -Ebene ist (siehe Abbildung 1 bis 3).
-Ebene ist (siehe Abbildung 1 bis 3).
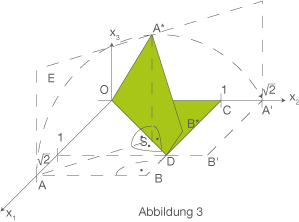
Während des Faltvorgangs wird das beim Falten bewegte Papier-Viereck auch in die Position des Vierecks - Leiten Sie je eine Gleichung dieser Ebene E in Parameterform und in Koordinatenform her.
Zur Kontrolle:
- Bestimmen Sie die Koordinaten des Schnittpunktes S der Ebene E mit der Geraden OD.
Zur Kontrolle: S
(8P + 6P)

c)
- Leiten Sie eine Gleichung der Ebene
in Parameterform her.
- Ermitteln Sie die Koordinaten des Punktes
.
(4P + 6P)
d)
- Begründen Sie, dass das Viereck
ein Drachenviereck ist.
- Ermitteln Sie den Flächeninhalt des Vierecks
.
(8P + 6P)
a)  Koordinaten des Mittelpunktes
Koordinaten des Mittelpunktes  angeben
Ein DIN-A4-Blatt wird entlang der Strecke
angeben
Ein DIN-A4-Blatt wird entlang der Strecke  gefaltet. Bestimme die Koordinaten des Mittelpunktes
gefaltet. Bestimme die Koordinaten des Mittelpunktes  der Strecke
der Strecke  .
Die Koordinaten des Mittelpunktes
.
Die Koordinaten des Mittelpunktes  zweier Punkte
zweier Punkte  und
und  kannst du folgendermaßen bestimmen:
kannst du folgendermaßen bestimmen:
 Das heißt, du benötigst die Koordinaten der Punkte
Das heißt, du benötigst die Koordinaten der Punkte  und
und  . Diese sind bereits im Aufgabentext angegeben mit:
. Diese sind bereits im Aufgabentext angegeben mit:
 zu erhalten, kannst du folgende Rechnung durchführen:
zu erhalten, kannst du folgende Rechnung durchführen:
 Die Koordinaten des Mittelpunktes
Die Koordinaten des Mittelpunktes  lauten
lauten  .
.
 Zeigen, dass Gerade
Zeigen, dass Gerade  senkrecht zur Geraden
senkrecht zur Geraden  ist
Um zu zeigen, dass eine Gerade
ist
Um zu zeigen, dass eine Gerade  senkrecht zu einer weiteren Geraden
senkrecht zu einer weiteren Geraden  ist, kannst du nachweisen, dass für das Skalarprodukt ihre Richtungsvektoren
ist, kannst du nachweisen, dass für das Skalarprodukt ihre Richtungsvektoren  und
und  folgender Zusammenhang erfüllt ist:
folgender Zusammenhang erfüllt ist:
 In unserem Fall kannst du
In unserem Fall kannst du  als Richtungsvektor der Geraden
als Richtungsvektor der Geraden  und
und  als Richtungsvektor der Geraden
als Richtungsvektor der Geraden  verwenden.
Du kannst dabei so vorgehen:
verwenden.
Du kannst dabei so vorgehen:
 entspricht gerade der Differenz
entspricht gerade der Differenz  :
:
 Der Richtungsvektor der Geraden
Der Richtungsvektor der Geraden  entspricht gerade der Differenz
entspricht gerade der Differenz  :
:
 2. Schritt: Skalarprodukt der Richtungsvektoren berechnen
Um herauszufinden, ob die Gerade
2. Schritt: Skalarprodukt der Richtungsvektoren berechnen
Um herauszufinden, ob die Gerade  senkrecht zur Geraden
senkrecht zur Geraden  ist, kannst du überprüfen, ob das Skalarprodukt ihrer Richtungsvektoren gleich Null ist:
ist, kannst du überprüfen, ob das Skalarprodukt ihrer Richtungsvektoren gleich Null ist:
 Damit ist das Skalarprodukt gleich Null und die Geraden sind senkrecht zueinander.
Damit ist das Skalarprodukt gleich Null und die Geraden sind senkrecht zueinander.
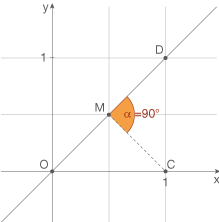
 Abstand des Punktes
Abstand des Punktes  von der Geraden
von der Geraden  bestimmen
bestimmen
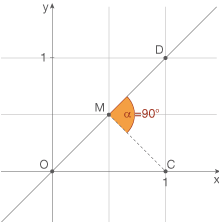 Der Abstand eines Punktes zu einer Geraden entspricht der kürzesten Strecke, die den Punkt mit der Geraden verbindet. Diese Strecke muss folglich senkrecht auf der Geraden stehen.
Aus dem Aufgabenteil zuvor weißt du, dass die Gerade
Der Abstand eines Punktes zu einer Geraden entspricht der kürzesten Strecke, die den Punkt mit der Geraden verbindet. Diese Strecke muss folglich senkrecht auf der Geraden stehen.
Aus dem Aufgabenteil zuvor weißt du, dass die Gerade  senkrecht auf der Geraden
senkrecht auf der Geraden  steht. Folglich entspricht der gesuchte Abstand gerade der Länge der Strecke
steht. Folglich entspricht der gesuchte Abstand gerade der Länge der Strecke  .
Die Länge l einer Strecke
.
Die Länge l einer Strecke  mit den Endpunkten
mit den Endpunkten  und
und  kannst du über den Betrag der Strecke berechnen:
kannst du über den Betrag der Strecke berechnen:
 Verwende diese Zusammenhang, um den Abstand des Punktes
Verwende diese Zusammenhang, um den Abstand des Punktes  zu bestimmen.
Damit ergibt sich für den Abstand des Punktes
zu bestimmen.
Damit ergibt sich für den Abstand des Punktes  zur Geraden
zur Geraden  bzw. der Länge der Strecke
bzw. der Länge der Strecke  :
:
 Die Strecke
Die Strecke  hat eine Länge von
hat eine Länge von  LE. Das heißt, der Abstand des Punktes
LE. Das heißt, der Abstand des Punktes  von der Geraden
von der Geraden  beträgt
beträgt  LE.
LE.
- Bestimme die Vektoren
und
.
- Berechne das Skalarprodukt der Vektoren. Erhältst du als Lösung den Wert Null, so sind die Geraden senkrecht zueinander.

b)  Gleichung der Ebene
Gleichung der Ebene  in Parameterform angeben
Das Blatt in der
in Parameterform angeben
Das Blatt in der  Ebene wird wie in Abbildung 1 und 2 gefaltet. Beim Faltvorgang „wandert“ der Punkt
Ebene wird wie in Abbildung 1 und 2 gefaltet. Beim Faltvorgang „wandert“ der Punkt  in die Position
in die Position  . Dabei bewegt sich der Punkt entlang eines Halbkreises. Die Ebene
. Dabei bewegt sich der Punkt entlang eines Halbkreises. Die Ebene  soll diesen Halbkreis enthalten und senkrecht zur
soll diesen Halbkreis enthalten und senkrecht zur  Ebene stehen.
Ebene stehen.
 Deine Aufgabe ist es, die Ebenengleichung zur Ebene
Deine Aufgabe ist es, die Ebenengleichung zur Ebene  in Parameterform anzugeben.
in Parameterform anzugeben.
Eine Ebenengleichung in Parameterform sieht wie folgt aus:
 Der Vektor
Der Vektor  wird Stützvektor genannt,
wird Stützvektor genannt,  und
und  sind die linear unabhängigen Spannvektoren der Ebene
sind die linear unabhängigen Spannvektoren der Ebene  .
Stelle die gesuchten Stütz- und Spannvektoren auf, um eine Ebenengleichung in Parameterform zu erhalten.
1. Schritt: Stützvektor der Ebene
.
Stelle die gesuchten Stütz- und Spannvektoren auf, um eine Ebenengleichung in Parameterform zu erhalten.
1. Schritt: Stützvektor der Ebene  aufstellen
Für den Stützvektor kannst du die Koordinaten eines Punktes verwenden, der garantiert in der Ebene liegt. Hier bietet sich beispielweise der Punkt
aufstellen
Für den Stützvektor kannst du die Koordinaten eines Punktes verwenden, der garantiert in der Ebene liegt. Hier bietet sich beispielweise der Punkt  an. Es ergibt sich also:
an. Es ergibt sich also:
 2. Schritt: Spannvektor
2. Schritt: Spannvektor  der Ebene
der Ebene  aufstellen
Da in der Aufgabenstellung verlangt wird, dass die Ebene
aufstellen
Da in der Aufgabenstellung verlangt wird, dass die Ebene  senkrecht auf der
senkrecht auf der  Ebene steht, kannst du einen der Spannvektoren direkt angeben, der diese Bedingung erfüllt:
Ebene steht, kannst du einen der Spannvektoren direkt angeben, der diese Bedingung erfüllt:
 3. Schritt: Spannvektor
3. Schritt: Spannvektor  der Ebene
der Ebene  aufstellen
Sollen weiterhin die Punkte
aufstellen
Sollen weiterhin die Punkte  und
und  in der Ebene
in der Ebene  enthalten sein, so muss auch ihre Verbindungsstrecke in der Ebene
enthalten sein, so muss auch ihre Verbindungsstrecke in der Ebene  liegen. Das heißt, du kannst den Vektor
liegen. Das heißt, du kannst den Vektor  als zweiten Spannvektor verwenden.
als zweiten Spannvektor verwenden.
 Offensichtlich benötigen wir die Koordinaten des Punktes
Offensichtlich benötigen wir die Koordinaten des Punktes  , um den zweiten Spannvektor angeben zu können. Wir erinnern uns: Das Blatt soll entlang der Geraden
, um den zweiten Spannvektor angeben zu können. Wir erinnern uns: Das Blatt soll entlang der Geraden  gefaltet werden. Das heißt, dass der Punkt
gefaltet werden. Das heißt, dass der Punkt  an der Geraden
an der Geraden  gespiegelt wird.
Anhand der Abbildung 3 kannst du die Koordinaten ablesen. Der Punkt
gespiegelt wird.
Anhand der Abbildung 3 kannst du die Koordinaten ablesen. Der Punkt  hat die Koordinaten
hat die Koordinaten  .
Damit kannst du nun den Vektor
.
Damit kannst du nun den Vektor  bestimmen:
bestimmen:
 4. Schritt: Aufgestellte Vektoren in Ebenengleichung einsetzen
Einsetzen des Stützvektors
4. Schritt: Aufgestellte Vektoren in Ebenengleichung einsetzen
Einsetzen des Stützvektors  und der Spannvektoren
und der Spannvektoren  und
und  in die allgemeine Form einer Ebenengleichung in Parameterform liefert dir die gesuchte Gleichung:
in die allgemeine Form einer Ebenengleichung in Parameterform liefert dir die gesuchte Gleichung:

 Gleichung der Ebene
Gleichung der Ebene  in Koordinatenform angeben
Eine Ebenengleichung in Koordinatenform ist allgemein von der Form:
in Koordinatenform angeben
Eine Ebenengleichung in Koordinatenform ist allgemein von der Form:
 Hast du bereits eine Ebenengleichung der Ebene in Parameterform, so kannst du die Koordinatenform ermitteln, indem du die Ebenengleichung in Parameterform mit
Hast du bereits eine Ebenengleichung der Ebene in Parameterform, so kannst du die Koordinatenform ermitteln, indem du die Ebenengleichung in Parameterform mit  ,
,  und
und  wie folgt gleichsetzt:
wie folgt gleichsetzt:
 Daraus erhältst du ein lineares Gleichungssystem, bei welchem du die Parameter
Daraus erhältst du ein lineares Gleichungssystem, bei welchem du die Parameter  und
und  eliminieren musst, um die Koordinatenform zu erhalten.
eliminieren musst, um die Koordinatenform zu erhalten.

 In der Gleichung
In der Gleichung  sind nun beide Parameter eliminiert. Das heißt, die Ebenengleichung zur Ebene
sind nun beide Parameter eliminiert. Das heißt, die Ebenengleichung zur Ebene  in Koordinatenform lautet:
in Koordinatenform lautet:

 Koordinaten des Schnittpunktes
Koordinaten des Schnittpunktes  bestimmen
Die Gerade
bestimmen
Die Gerade  schneidet die Ebene
schneidet die Ebene  in einem Punkt
in einem Punkt  . Um den Schnittpunkt einer Geraden mit einer Ebene zu ermitteln, kannst du die Geradengleichung komponentenweise in die zuvor bestimme Ebenengleichung in Parameterform einsetzen.
Eine Gleichung der Geraden
. Um den Schnittpunkt einer Geraden mit einer Ebene zu ermitteln, kannst du die Geradengleichung komponentenweise in die zuvor bestimme Ebenengleichung in Parameterform einsetzen.
Eine Gleichung der Geraden  könnte zum Beispiel so aussehen:
könnte zum Beispiel so aussehen:
 Dabei wurde der Ortsvektor
Dabei wurde der Ortsvektor  verwendet. Gehe also wie folgt vor:
verwendet. Gehe also wie folgt vor:
 mit Ebenengleichung von
mit Ebenengleichung von  gleichsetzen
Komponentenweise Gleichsetzen der Geradengleichung mit der Ebenengleichung von
gleichsetzen
Komponentenweise Gleichsetzen der Geradengleichung mit der Ebenengleichung von  liefert dir folgendes lineares Gleichungssystem, welches du nach
liefert dir folgendes lineares Gleichungssystem, welches du nach  auflösen sollst:
auflösen sollst:


 Du erhältst
Du erhältst  .
2. Schritt: Parameter
.
2. Schritt: Parameter  in Geradengleichung von
in Geradengleichung von  einsetzen
Einsetzen von
einsetzen
Einsetzen von  in die Geradengleichung zu
in die Geradengleichung zu  liefert dir die Koordinaten des Schnittpunktes
liefert dir die Koordinaten des Schnittpunktes  :
:
 Der Schnittpunkt
Der Schnittpunkt  besitzt die Koordinaten
besitzt die Koordinaten  .
.


Eine Ebenengleichung in Parameterform sieht wie folgt aus:
- Setze diese Geradengleichung in die Ebenengleichung von
gleich und löse nach dem Parameter
auf. Dadurch erhältst du einen Wert für den Parameter
.
- Setze diesen Parameterwert für
anschließend in die Geradengleichung von
ein. Das liefert dir die Koordinaten des gesuchten Schnittpunktes
.
c)  Gleichung der Ebene
Gleichung der Ebene  in Parameterform bestimmen
in Parameterform bestimmen
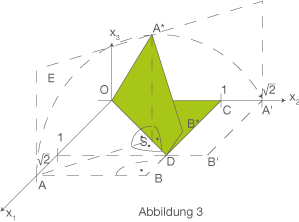 Während des Faltvorgangs nehmen die Punkte
Während des Faltvorgangs nehmen die Punkte  und
und  die Positionen
die Positionen  und
und  ein.
Eine neue Ebene
ein.
Eine neue Ebene  soll nun das daraus entstehende Viereck
soll nun das daraus entstehende Viereck  enthalten. Weiterhin ist diese Ebene
enthalten. Weiterhin ist diese Ebene  senkrecht zur
senkrecht zur  Ebene und zur Ebene
Ebene und zur Ebene  .
Deine Aufgabe ist es, die Gleichung der Ebene
.
Deine Aufgabe ist es, die Gleichung der Ebene  in Parameterform aufzustellen.
Eine Ebenengleichung in Parameterform sieht wie folgt aus:
in Parameterform aufzustellen.
Eine Ebenengleichung in Parameterform sieht wie folgt aus:
 Der Vektor
Der Vektor  wird Stützvektor genannt,
wird Stützvektor genannt,  und
und  sind die linear unabhängigen Spannvektoren der Ebene
sind die linear unabhängigen Spannvektoren der Ebene  .
Stelle die gesuchten Stütz- und Spannvektoren auf, um eine Ebenengleichung in Parameterform zu erhalten.
1. Schritt: Stützvektor der Ebene
.
Stelle die gesuchten Stütz- und Spannvektoren auf, um eine Ebenengleichung in Parameterform zu erhalten.
1. Schritt: Stützvektor der Ebene  aufstellen
Für den Stützvektor kannst du die Koordinaten eines Punktes verwenden, der garantiert in der Ebene liegt. Hier bietet sich beispielweise der Punkt
aufstellen
Für den Stützvektor kannst du die Koordinaten eines Punktes verwenden, der garantiert in der Ebene liegt. Hier bietet sich beispielweise der Punkt  an. Es ergibt sich also:
an. Es ergibt sich also:
 2. Schritt: Spannvektor
2. Schritt: Spannvektor  der Ebene
der Ebene  aufstellen
Da in der Aufgabenstellung verlangt wird, dass die Ebene
aufstellen
Da in der Aufgabenstellung verlangt wird, dass die Ebene  senkrecht auf der
senkrecht auf der  Ebene steht, kannst du einen der Spannvektoren direkt angeben, der diese Bedingung erfüllt:
Ebene steht, kannst du einen der Spannvektoren direkt angeben, der diese Bedingung erfüllt:
 3. Schritt: Spannvektor
3. Schritt: Spannvektor  der Ebene
der Ebene  aufstellen
Soll die Ebene
aufstellen
Soll die Ebene  senkrecht zur Ebene
senkrecht zur Ebene  sein, so muss
sein, so muss  den Normalenvektor der Ebene
den Normalenvektor der Ebene  enthalten.
Den Normalenvektor der Ebene
enthalten.
Den Normalenvektor der Ebene  kannst du an der Ebenengleichung in Koordinatenform direkt ablesen.
kannst du an der Ebenengleichung in Koordinatenform direkt ablesen.
 Der gesuchte Spannvektor lautet also:
Der gesuchte Spannvektor lautet also:
 4. Schritt: Aufgestellte Vektoren in Ebenengleichung einsetzen
Einsetzen des Stützvektors
4. Schritt: Aufgestellte Vektoren in Ebenengleichung einsetzen
Einsetzen des Stützvektors  und der Spannvektoren
und der Spannvektoren  und
und  in die allgemeine Form einer Ebenengleichung in Parameterform liefert dir die gesuchte Gleichung:
in die allgemeine Form einer Ebenengleichung in Parameterform liefert dir die gesuchte Gleichung:

 Koordinaten des Punktes
Koordinaten des Punktes  ermitteln
Der Punkt
ermitteln
Der Punkt  liegt laut Voraussetzung in den Ebenen
liegt laut Voraussetzung in den Ebenen  und
und  . Folglich muss dieser Punkt ebenfalls auf der Schnittgeraden
. Folglich muss dieser Punkt ebenfalls auf der Schnittgeraden  der Ebenen liegen.
Im Punkt
der Ebenen liegen.
Im Punkt  schneidet die Ebene
schneidet die Ebene  die Gerade
die Gerade  , an welcher das Blatt gefaltet wird. Durch das Falten bewegt sich der Punkt
, an welcher das Blatt gefaltet wird. Durch das Falten bewegt sich der Punkt  entlang eines Halbkreises um den Punkt
entlang eines Halbkreises um den Punkt  und nimmt entlang dieses Halbkreises die Position
und nimmt entlang dieses Halbkreises die Position  ein. Das heißt, der Punkt
ein. Das heißt, der Punkt  hat den selben Abstand zum Punkt
hat den selben Abstand zum Punkt  wie der gesuchte Punkt
wie der gesuchte Punkt  , es gilt also
, es gilt also  .
.
 Du kann also wie folgt vorgehen, um die Koordinaten des Punktes
Du kann also wie folgt vorgehen, um die Koordinaten des Punktes  zu bestimmen:
zu bestimmen:
 der Ebenen
der Ebenen  und
und  bestimmen
Die Schnittgerade erhältst du, indem du beide Ebenengleichungen gleichsetzt.
bestimmen
Die Schnittgerade erhältst du, indem du beide Ebenengleichungen gleichsetzt.
 Dadurch erhältst du ein lineares Gleichungssystem.
Dadurch erhältst du ein lineares Gleichungssystem.
 Setze entweder
Setze entweder  in die Ebenengleichung zu
in die Ebenengleichung zu  oder
oder  in die Ebenengleichung zu
in die Ebenengleichung zu  ein, um die Schnittgerade zu erhalten.
Wir setzen hierbei nun
ein, um die Schnittgerade zu erhalten.
Wir setzen hierbei nun  in die Ebenengleichung von
in die Ebenengleichung von  ein:
ein:
 Da der Punkt
Da der Punkt  auf der Schnittgeraden
auf der Schnittgeraden  liegt, kannst du die Koordinaten des Punktes
liegt, kannst du die Koordinaten des Punktes  in Abhängigkeit vom Parameter
in Abhängigkeit vom Parameter  angeben mit:
angeben mit:
 2. Schritt: Verwenden, dass
2. Schritt: Verwenden, dass  gelten muss
Offensichtlich ist nur noch die
gelten muss
Offensichtlich ist nur noch die  -Koordinate vom Parameter
-Koordinate vom Parameter  abhängig. Einen passenden Wert für
abhängig. Einen passenden Wert für  kannst du mit Hilfe der Bedingung
kannst du mit Hilfe der Bedingung  bestimmen.
Den Betrag
bestimmen.
Den Betrag  kannst du bereits berechnen, da dir die Koordinaten beider Punkte bekannt sind:
kannst du bereits berechnen, da dir die Koordinaten beider Punkte bekannt sind:
 Damit gilt
Damit gilt  und wir können diese Bedingung im Folgenden weiterverwenden:
und wir können diese Bedingung im Folgenden weiterverwenden:
 Damit muss
Damit muss  gelten. Nun kannst du die Koordinaten des Punktes
gelten. Nun kannst du die Koordinaten des Punktes  vollständig angeben:
vollständig angeben: 


- Bestimme die Schnittgerade
der Ebenen
und
. (Dadurch erhältst du zunächst die erste und zweite Koordinate von
).
- Verwende, dass
gilt, um die dritte Koordinate zu bestimmen.
d)  Begründen, dass das Viereck
Begründen, dass das Viereck  ein Drachenviereck ist
Zeige, dass das in der
ein Drachenviereck ist
Zeige, dass das in der  Ebene liegende Viereck
Ebene liegende Viereck  ein Drachenviereck ist. Soll
ein Drachenviereck ist. Soll  ein Drachenviereck sein, so muss folgende Bedingung erfüllt werden:
ein Drachenviereck sein, so muss folgende Bedingung erfüllt werden:
 Berechne die Beträge der Strecken und begründe anhand des Resultats, dass bei
Berechne die Beträge der Strecken und begründe anhand des Resultats, dass bei  ein Drachenviereck vorliegt.
Aus dem Aufgabenteil zuvor weißt du, dass
ein Drachenviereck vorliegt.
Aus dem Aufgabenteil zuvor weißt du, dass  gilt.
gilt.

![\(\begin{array}{rll}
\mid \overrightarrow{AB} \mid&=&\left| \begin{pmatrix}
\sqrt{2}\\
1\\
0
\end{pmatrix} - \begin{pmatrix}
\sqrt{2}\\
0\\
0
\end{pmatrix} \right|\\[5pt]
&=& \left| \begin{pmatrix}
0\\
1\\
0
\end{pmatrix} \right|\\[5pt]
&=& \sqrt{0^2+1^2+0^2}\\[5pt]
&=&1\\\end{array}\)](https://www.schullv.de/resources/formulas/04e86fe2cb0f8da3a2bf9603cb8477a018532f94e06f985589ae29add5abf2ff_light.svg)
![\(\begin{array}{rll}
\mid \overrightarrow{DB} \mid&=& \left| \begin{pmatrix}
\sqrt{2}\\
1\\
0
\end{pmatrix} - \begin{pmatrix}
1\\
1\\
0
\end{pmatrix} \right|\\[5pt]
&=& \left| \begin{pmatrix}
\sqrt{2}-1\\
0\\
0
\end{pmatrix} \right|\\[5pt]
&=& \sqrt{\left(\sqrt{2}-1\right)^2+0^2+0^2}\\[5pt]
&=&\sqrt{2}-1\\
\end{array}\)](https://www.schullv.de/resources/formulas/c05ec5f32d4721ad625f41e7005b9d960b7362c5b2a5de658a23483688056e99_light.svg)
![\(\begin{array}{rll}
\mid \overrightarrow{DS} \mid&=& \left| \begin{pmatrix}
\frac{1}{2}\sqrt{2}\\
\frac{1}{2}\sqrt{2}\\
0
\end{pmatrix} - \begin{pmatrix}
1\\
1\\
0
\end{pmatrix} \right|\\[5pt]
&=& \left| \begin{pmatrix}
\frac{1}{2}\sqrt{2}-1\\
\frac{1}{2}\sqrt{2}-1\\
0
\end{pmatrix} \right|\\[5pt]
&=& \sqrt{\left(\frac{1}{2}\sqrt{2}-1\right)^2+\left(\frac{1}{2}\sqrt{2}-1\right)^2+0^2}\\[5pt]
&=&\sqrt{2}-1\\
\end{array}\)](https://www.schullv.de/resources/formulas/769f25b9ab9d15e052a610f2c6dc56b6e5d3be2ed359a7ae254c565fa122832f_light.svg) Damit hast du gezeigt, dass
Damit hast du gezeigt, dass  gilt und damit auch, dass es sich bei
gilt und damit auch, dass es sich bei  um ein Drachenviereck handelt.
um ein Drachenviereck handelt.
 Flächeninhalt des Vierecks
Flächeninhalt des Vierecks  bestimmen
Im Aufgabenteil zuvor hast du gezeigt, dass es sich bei
bestimmen
Im Aufgabenteil zuvor hast du gezeigt, dass es sich bei  um ein Drachenviereck handelt. Um nun den Flächeninhalt von
um ein Drachenviereck handelt. Um nun den Flächeninhalt von  zu bestimmen, kannst du die Formel für den Flächeninhalt
zu bestimmen, kannst du die Formel für den Flächeninhalt  eines Drachenvierecks verwenden:
eines Drachenvierecks verwenden:
 Bestimme die Beträge der Vektoren und setze diese in die oben genannte Formel ein, um den Flächeninhalt zu erhalten.
1. Schritt: Beträge der Vektoren bestimmen
Bestimme die Beträge der Vektoren und setze diese in die oben genannte Formel ein, um den Flächeninhalt zu erhalten.
1. Schritt: Beträge der Vektoren bestimmen
![\(\begin{array}{rll}
\left| \overrightarrow{AD} \right|&=& \left| \begin{pmatrix}
1\\
1\\
0
\end{pmatrix} - \begin{pmatrix}
\sqrt{2}\\
0\\
0
\end{pmatrix} \right|\\[5pt]
&=& \left| \begin{pmatrix}
1-\sqrt{2}\\
1\\
0
\end{pmatrix} \right|\\[5pt]
&=& \sqrt{(1-\sqrt{2})^2+1^2+0^2}\\[5pt]
&=&\sqrt{4-2 \cdot \sqrt{2}}\\
\end{array}\)](https://www.schullv.de/resources/formulas/c87bc77085726a6e0223bf17b70870b661a0639ed359addee27fe5f91bd4bc73_light.svg)
![\(\begin{array}{rll}
\mid \overrightarrow{SB} \mid&=& \left| \begin{pmatrix}
\sqrt{2}\\
1\\
0
\end{pmatrix} - \begin{pmatrix}
\frac{1}{2} \cdot \sqrt{2}\\
\frac{1}{2} \cdot \sqrt{2}\\
0
\end{pmatrix} \right|\\[5pt]
&=& \left| \begin{pmatrix}
\frac{1}{2} \cdot \sqrt{2}\\
1-\frac{1}{2} \cdot \sqrt{2}\\
0
\end{pmatrix} \right|\\[5pt]
&=& \sqrt{\left(\frac{1}{2} \cdot \sqrt{2}\right)^2+\left( 1-\frac{1}{2} \cdot \sqrt{2} \right)^2+0^2}\\[5pt]
&=&\sqrt{2-\sqrt{2}}\\
\end{array}\)](https://www.schullv.de/resources/formulas/a213a2a7e26af7722e0aa59a2b736ec9f647e4153f81b2b47de8580b2c2a44eb_light.svg) 2. Schritt: In Formel für Flächeninhalt einsetzen
Setze die berechneten Beträge in die oben genannte Formel ein:
2. Schritt: In Formel für Flächeninhalt einsetzen
Setze die berechneten Beträge in die oben genannte Formel ein:
 Der Flächeninhalt des Vierecks
Der Flächeninhalt des Vierecks  beträgt
beträgt  FE.
FE.
a)  Koordinaten des Mittelpunktes
Koordinaten des Mittelpunktes  angeben
Ein DIN-A4-Blatt wird entlang der Strecke
angeben
Ein DIN-A4-Blatt wird entlang der Strecke  gefaltet. Bestimme die Koordinaten des Mittelpunktes
gefaltet. Bestimme die Koordinaten des Mittelpunktes  der Strecke
der Strecke  .
Die Koordinaten des Mittelpunktes
.
Die Koordinaten des Mittelpunktes  zweier Punkte
zweier Punkte  und
und  kannst du folgendermaßen bestimmen:
kannst du folgendermaßen bestimmen:
 Das heißt, du benötigst die Koordinaten der Punkte
Das heißt, du benötigst die Koordinaten der Punkte  und
und  . Diese sind bereits im Aufgabentext angegeben mit:
. Diese sind bereits im Aufgabentext angegeben mit:
 zu erhalten, kannst du folgende Rechnung durchführen:
zu erhalten, kannst du folgende Rechnung durchführen:
 Die Koordinaten des Mittelpunktes
Die Koordinaten des Mittelpunktes  lauten
lauten  .
.
 Zeigen, dass Gerade
Zeigen, dass Gerade  senkrecht zur Geraden
senkrecht zur Geraden  ist
Um zu zeigen, dass eine Gerade
ist
Um zu zeigen, dass eine Gerade  senkrecht zu einer weiteren Geraden
senkrecht zu einer weiteren Geraden  ist, kannst du nachweisen, dass für das Skalarprodukt ihre Richtungsvektoren
ist, kannst du nachweisen, dass für das Skalarprodukt ihre Richtungsvektoren  und
und  folgender Zusammenhang erfüllt ist:
folgender Zusammenhang erfüllt ist:
 In unserem Fall kannst du
In unserem Fall kannst du  als Richtungsvektor der Geraden
als Richtungsvektor der Geraden  und
und  als Richtungsvektor der Geraden
als Richtungsvektor der Geraden  verwenden.
Du kannst dabei so vorgehen:
verwenden.
Du kannst dabei so vorgehen:
 entspricht gerade der Differenz
entspricht gerade der Differenz  :
:
 Der Richtungsvektor der Geraden
Der Richtungsvektor der Geraden  entspricht gerade der Differenz
entspricht gerade der Differenz  :
:
 2. Schritt: Skalarprodukt der Richtungsvektoren berechnen
Um herauszufinden, ob die Gerade
2. Schritt: Skalarprodukt der Richtungsvektoren berechnen
Um herauszufinden, ob die Gerade  senkrecht zur Geraden
senkrecht zur Geraden  ist, kannst du überprüfen, ob das Skalarprodukt ihrer Richtungsvektoren gleich Null ist:
ist, kannst du überprüfen, ob das Skalarprodukt ihrer Richtungsvektoren gleich Null ist:
 Damit ist das Skalarprodukt gleich Null und die Geraden sind senkrecht zueinander.
Damit ist das Skalarprodukt gleich Null und die Geraden sind senkrecht zueinander.
 Abstand des Punktes
Abstand des Punktes  von der Geraden
von der Geraden  bestimmen
bestimmen
 Der Abstand eines Punktes zu einer Geraden entspricht der kürzesten Strecke, die den Punkt mit der Geraden verbindet. Diese Strecke muss folglich senkrecht auf der Geraden stehen.
Aus dem Aufgabenteil zuvor weißt du, dass die Gerade
Der Abstand eines Punktes zu einer Geraden entspricht der kürzesten Strecke, die den Punkt mit der Geraden verbindet. Diese Strecke muss folglich senkrecht auf der Geraden stehen.
Aus dem Aufgabenteil zuvor weißt du, dass die Gerade  senkrecht auf der Geraden
senkrecht auf der Geraden  steht. Folglich entspricht der gesuchte Abstand gerade der Länge der Strecke
steht. Folglich entspricht der gesuchte Abstand gerade der Länge der Strecke  .
Die Länge l einer Strecke
.
Die Länge l einer Strecke  mit den Endpunkten
mit den Endpunkten  und
und  kannst du über den Betrag der Strecke berechnen:
kannst du über den Betrag der Strecke berechnen:
 Verwende diese Zusammenhang, um den Abstand des Punktes
Verwende diese Zusammenhang, um den Abstand des Punktes  zu bestimmen.
Damit ergibt sich für den Abstand des Punktes
zu bestimmen.
Damit ergibt sich für den Abstand des Punktes  zur Geraden
zur Geraden  bzw. der Länge der Strecke
bzw. der Länge der Strecke  :
:
 Die Strecke
Die Strecke  hat eine Länge von
hat eine Länge von  LE. Das heißt, der Abstand des Punktes
LE. Das heißt, der Abstand des Punktes  von der Geraden
von der Geraden  beträgt
beträgt  LE.
LE.
- Bestimme die Vektoren
und
.
- Berechne das Skalarprodukt der Vektoren. Erhältst du als Lösung den Wert Null, so sind die Geraden senkrecht zueinander.

b)  Gleichung der Ebene
Gleichung der Ebene  in Parameterform angeben
Das Blatt in der
in Parameterform angeben
Das Blatt in der  Ebene wird wie in Abbildung 1 und 2 gefaltet. Beim Faltvorgang „wandert“ der Punkt
Ebene wird wie in Abbildung 1 und 2 gefaltet. Beim Faltvorgang „wandert“ der Punkt  in die Position
in die Position  . Dabei bewegt sich der Punkt entlang eines Halbkreises. Die Ebene
. Dabei bewegt sich der Punkt entlang eines Halbkreises. Die Ebene  soll diesen Halbkreis enthalten und senkrecht zur
soll diesen Halbkreis enthalten und senkrecht zur  Ebene stehen.
Ebene stehen.

 Deine Aufgabe ist es, die Ebenengleichung zur Ebene
Deine Aufgabe ist es, die Ebenengleichung zur Ebene  in Parameterform anzugeben.
in Parameterform anzugeben.
Eine Ebenengleichung in Parameterform sieht wie folgt aus:
 Der Vektor
Der Vektor  wird Stützvektor genannt,
wird Stützvektor genannt,  und
und  sind die linear unabhängigen Spannvektoren der Ebene
sind die linear unabhängigen Spannvektoren der Ebene  .
Stelle die gesuchten Stütz- und Spannvektoren auf, um eine Ebenengleichung in Parameterform zu erhalten.
1. Schritt: Stützvektor der Ebene
.
Stelle die gesuchten Stütz- und Spannvektoren auf, um eine Ebenengleichung in Parameterform zu erhalten.
1. Schritt: Stützvektor der Ebene  aufstellen
Für den Stützvektor kannst du die Koordinaten eines Punktes verwenden, der garantiert in der Ebene liegt. Hier bietet sich beispielweise der Punkt
aufstellen
Für den Stützvektor kannst du die Koordinaten eines Punktes verwenden, der garantiert in der Ebene liegt. Hier bietet sich beispielweise der Punkt  an. Es ergibt sich also:
an. Es ergibt sich also:
 2. Schritt: Spannvektor
2. Schritt: Spannvektor  der Ebene
der Ebene  aufstellen
Da in der Aufgabenstellung verlangt wird, dass die Ebene
aufstellen
Da in der Aufgabenstellung verlangt wird, dass die Ebene  senkrecht auf der
senkrecht auf der  Ebene steht, kannst du einen der Spannvektoren direkt angeben, der diese Bedingung erfüllt:
Ebene steht, kannst du einen der Spannvektoren direkt angeben, der diese Bedingung erfüllt:
 3. Schritt: Spannvektor
3. Schritt: Spannvektor  der Ebene
der Ebene  aufstellen
Sollen weiterhin die Punkte
aufstellen
Sollen weiterhin die Punkte  und
und  in der Ebene
in der Ebene  enthalten sein, so muss auch ihre Verbindungsstrecke in der Ebene
enthalten sein, so muss auch ihre Verbindungsstrecke in der Ebene  liegen. Das heißt, du kannst den Vektor
liegen. Das heißt, du kannst den Vektor  als zweiten Spannvektor verwenden.
als zweiten Spannvektor verwenden.
 Offensichtlich benötigen wir die Koordinaten des Punktes
Offensichtlich benötigen wir die Koordinaten des Punktes  , um den zweiten Spannvektor angeben zu können. Wir erinnern uns: Das Blatt soll entlang der Geraden
, um den zweiten Spannvektor angeben zu können. Wir erinnern uns: Das Blatt soll entlang der Geraden  gefaltet werden. Das heißt, dass der Punkt
gefaltet werden. Das heißt, dass der Punkt  an der Geraden
an der Geraden  gespiegelt wird.
Anhand der Abbildung 3 kannst du die Koordinaten ablesen. Der Punkt
gespiegelt wird.
Anhand der Abbildung 3 kannst du die Koordinaten ablesen. Der Punkt  hat die Koordinaten
hat die Koordinaten  .
Damit kannst du nun den Vektor
.
Damit kannst du nun den Vektor  bestimmen:
bestimmen:
 4. Schritt: Aufgestellte Vektoren in Ebenengleichung einsetzen
Einsetzen des Stützvektors
4. Schritt: Aufgestellte Vektoren in Ebenengleichung einsetzen
Einsetzen des Stützvektors  und der Spannvektoren
und der Spannvektoren  und
und  in die allgemeine Form einer Ebenengleichung in Parameterform liefert dir die gesuchte Gleichung:
in die allgemeine Form einer Ebenengleichung in Parameterform liefert dir die gesuchte Gleichung:

 Gleichung der Ebene
Gleichung der Ebene  in Koordinatenform angeben
Eine Ebenengleichung in Koordinatenform ist allgemein von der Form:
in Koordinatenform angeben
Eine Ebenengleichung in Koordinatenform ist allgemein von der Form:
 Hast du bereits eine Ebenengleichung der Ebene in Parameterform, so kannst du die Koordinatenform ermitteln, indem du die Ebenengleichung in Parameterform mit
Hast du bereits eine Ebenengleichung der Ebene in Parameterform, so kannst du die Koordinatenform ermitteln, indem du die Ebenengleichung in Parameterform mit  ,
,  und
und  wie folgt gleichsetzt:
wie folgt gleichsetzt:
 Daraus erhältst du ein lineares Gleichungssystem, bei welchem du die Parameter
Daraus erhältst du ein lineares Gleichungssystem, bei welchem du die Parameter  und
und  eliminieren musst, um die Koordinatenform zu erhalten.
eliminieren musst, um die Koordinatenform zu erhalten.

 In der Gleichung
In der Gleichung  sind nun beide Parameter eliminiert. Das heißt, die Ebenengleichung zur Ebene
sind nun beide Parameter eliminiert. Das heißt, die Ebenengleichung zur Ebene  in Koordinatenform lautet:
in Koordinatenform lautet:

 Koordinaten des Schnittpunktes
Koordinaten des Schnittpunktes  bestimmen
Die Gerade
bestimmen
Die Gerade  schneidet die Ebene
schneidet die Ebene  in einem Punkt
in einem Punkt  . Um den Schnittpunkt einer Geraden mit einer Ebene zu ermitteln, kannst du die Geradengleichung komponentenweise in die zuvor bestimme Ebenengleichung in Parameterform einsetzen.
Eine Gleichung der Geraden
. Um den Schnittpunkt einer Geraden mit einer Ebene zu ermitteln, kannst du die Geradengleichung komponentenweise in die zuvor bestimme Ebenengleichung in Parameterform einsetzen.
Eine Gleichung der Geraden  könnte zum Beispiel so aussehen:
könnte zum Beispiel so aussehen:
 Dabei wurde der Ortsvektor
Dabei wurde der Ortsvektor  verwendet. Gehe also wie folgt vor:
verwendet. Gehe also wie folgt vor:
 mit Ebenengleichung von
mit Ebenengleichung von  gleichsetzen
Komponentenweise Gleichsetzen der Geradengleichung mit der Ebenengleichung von
gleichsetzen
Komponentenweise Gleichsetzen der Geradengleichung mit der Ebenengleichung von  liefert dir folgendes lineares Gleichungssystem, welches du nach
liefert dir folgendes lineares Gleichungssystem, welches du nach  auflösen sollst:
auflösen sollst:


 Du erhältst
Du erhältst  .
2. Schritt: Parameter
.
2. Schritt: Parameter  in Geradengleichung von
in Geradengleichung von  einsetzen
Einsetzen von
einsetzen
Einsetzen von  in die Geradengleichung zu
in die Geradengleichung zu  liefert dir die Koordinaten des Schnittpunktes
liefert dir die Koordinaten des Schnittpunktes  :
:
 Der Schnittpunkt
Der Schnittpunkt  besitzt die Koordinaten
besitzt die Koordinaten  .
.


Eine Ebenengleichung in Parameterform sieht wie folgt aus:
- Setze diese Geradengleichung in die Ebenengleichung von
gleich und löse nach dem Parameter
auf. Dadurch erhältst du einen Wert für den Parameter
.
- Setze diesen Parameterwert für
anschließend in die Geradengleichung von
ein. Das liefert dir die Koordinaten des gesuchten Schnittpunktes
.
c)  Gleichung der Ebene
Gleichung der Ebene  in Parameterform bestimmen
in Parameterform bestimmen
 Während des Faltvorgangs nehmen die Punkte
Während des Faltvorgangs nehmen die Punkte  und
und  die Positionen
die Positionen  und
und  ein.
Eine neue Ebene
ein.
Eine neue Ebene  soll nun das daraus entstehende Viereck
soll nun das daraus entstehende Viereck  enthalten. Weiterhin ist diese Ebene
enthalten. Weiterhin ist diese Ebene  senkrecht zur
senkrecht zur  Ebene und zur Ebene
Ebene und zur Ebene  .
Deine Aufgabe ist es, die Gleichung der Ebene
.
Deine Aufgabe ist es, die Gleichung der Ebene  in Parameterform aufzustellen.
Eine Ebenengleichung in Parameterform sieht wie folgt aus:
in Parameterform aufzustellen.
Eine Ebenengleichung in Parameterform sieht wie folgt aus:
 Der Vektor
Der Vektor  wird Stützvektor genannt,
wird Stützvektor genannt,  und
und  sind die linear unabhängigen Spannvektoren der Ebene
sind die linear unabhängigen Spannvektoren der Ebene  .
Stelle die gesuchten Stütz- und Spannvektoren auf, um eine Ebenengleichung in Parameterform zu erhalten.
1. Schritt: Stützvektor der Ebene
.
Stelle die gesuchten Stütz- und Spannvektoren auf, um eine Ebenengleichung in Parameterform zu erhalten.
1. Schritt: Stützvektor der Ebene  aufstellen
Für den Stützvektor kannst du die Koordinaten eines Punktes verwenden, der garantiert in der Ebene liegt. Hier bietet sich beispielweise der Punkt
aufstellen
Für den Stützvektor kannst du die Koordinaten eines Punktes verwenden, der garantiert in der Ebene liegt. Hier bietet sich beispielweise der Punkt  an. Es ergibt sich also:
an. Es ergibt sich also:
 2. Schritt: Spannvektor
2. Schritt: Spannvektor  der Ebene
der Ebene  aufstellen
Da in der Aufgabenstellung verlangt wird, dass die Ebene
aufstellen
Da in der Aufgabenstellung verlangt wird, dass die Ebene  senkrecht auf der
senkrecht auf der  Ebene steht, kannst du einen der Spannvektoren direkt angeben, der diese Bedingung erfüllt:
Ebene steht, kannst du einen der Spannvektoren direkt angeben, der diese Bedingung erfüllt:
 3. Schritt: Spannvektor
3. Schritt: Spannvektor  der Ebene
der Ebene  aufstellen
Soll die Ebene
aufstellen
Soll die Ebene  senkrecht zur Ebene
senkrecht zur Ebene  sein, so muss
sein, so muss  den Normalenvektor der Ebene
den Normalenvektor der Ebene  enthalten.
Den Normalenvektor der Ebene
enthalten.
Den Normalenvektor der Ebene  kannst du an der Ebenengleichung in Koordinatenform direkt ablesen.
kannst du an der Ebenengleichung in Koordinatenform direkt ablesen.
 Der gesuchte Spannvektor lautet also:
Der gesuchte Spannvektor lautet also:
 4. Schritt: Aufgestellte Vektoren in Ebenengleichung einsetzen
Einsetzen des Stützvektors
4. Schritt: Aufgestellte Vektoren in Ebenengleichung einsetzen
Einsetzen des Stützvektors  und der Spannvektoren
und der Spannvektoren  und
und  in die allgemeine Form einer Ebenengleichung in Parameterform liefert dir die gesuchte Gleichung:
in die allgemeine Form einer Ebenengleichung in Parameterform liefert dir die gesuchte Gleichung:

 Koordinaten des Punktes
Koordinaten des Punktes  ermitteln
Der Punkt
ermitteln
Der Punkt  liegt laut Voraussetzung in den Ebenen
liegt laut Voraussetzung in den Ebenen  und
und  . Folglich muss dieser Punkt ebenfalls auf der Schnittgeraden
. Folglich muss dieser Punkt ebenfalls auf der Schnittgeraden  der Ebenen liegen.
Im Punkt
der Ebenen liegen.
Im Punkt  schneidet die Ebene
schneidet die Ebene  die Gerade
die Gerade  , an welcher das Blatt gefaltet wird. Durch das Falten bewegt sich der Punkt
, an welcher das Blatt gefaltet wird. Durch das Falten bewegt sich der Punkt  entlang eines Halbkreises um den Punkt
entlang eines Halbkreises um den Punkt  und nimmt entlang dieses Halbkreises die Position
und nimmt entlang dieses Halbkreises die Position  ein. Das heißt, der Punkt
ein. Das heißt, der Punkt  hat den selben Abstand zum Punkt
hat den selben Abstand zum Punkt  wie der gesuchte Punkt
wie der gesuchte Punkt  , es gilt also
, es gilt also  .
.
 Du kann also wie folgt vorgehen, um die Koordinaten des Punktes
Du kann also wie folgt vorgehen, um die Koordinaten des Punktes  zu bestimmen:
zu bestimmen:
 der Ebenen
der Ebenen  und
und  bestimmen
Die Schnittgerade erhältst du, indem du beide Ebenengleichungen gleichsetzt.
bestimmen
Die Schnittgerade erhältst du, indem du beide Ebenengleichungen gleichsetzt.
 Dadurch erhältst du ein lineares Gleichungssystem.
Dadurch erhältst du ein lineares Gleichungssystem.
 Setze entweder
Setze entweder  in die Ebenengleichung zu
in die Ebenengleichung zu  oder
oder  in die Ebenengleichung zu
in die Ebenengleichung zu  ein, um die Schnittgerade zu erhalten.
Wir setzen hierbei nun
ein, um die Schnittgerade zu erhalten.
Wir setzen hierbei nun  in die Ebenengleichung von
in die Ebenengleichung von  ein:
ein:
 Da der Punkt
Da der Punkt  auf der Schnittgeraden
auf der Schnittgeraden  liegt, kannst du die Koordinaten des Punktes
liegt, kannst du die Koordinaten des Punktes  in Abhängigkeit vom Parameter
in Abhängigkeit vom Parameter  angeben mit:
angeben mit:
 2. Schritt: Verwenden, dass
2. Schritt: Verwenden, dass  gelten muss
Offensichtlich ist nur noch die
gelten muss
Offensichtlich ist nur noch die  -Koordinate vom Parameter
-Koordinate vom Parameter  abhängig. Einen passenden Wert für
abhängig. Einen passenden Wert für  kannst du mit Hilfe der Bedingung
kannst du mit Hilfe der Bedingung  bestimmen.
Den Betrag
bestimmen.
Den Betrag  kannst du bereits berechnen, da dir die Koordinaten beider Punkte bekannt sind:
kannst du bereits berechnen, da dir die Koordinaten beider Punkte bekannt sind:
 Damit gilt
Damit gilt  und wir können diese Bedingung im Folgenden weiterverwenden:
und wir können diese Bedingung im Folgenden weiterverwenden:
 Damit muss
Damit muss  gelten. Nun kannst du die Koordinaten des Punktes
gelten. Nun kannst du die Koordinaten des Punktes  vollständig angeben:
vollständig angeben: 


- Bestimme die Schnittgerade
der Ebenen
und
. (Dadurch erhältst du zunächst die erste und zweite Koordinate von
).
- Verwende, dass
gilt, um die dritte Koordinate zu bestimmen.
d)  Begründen, dass das Viereck
Begründen, dass das Viereck  ein Drachenviereck ist
Zeige, dass das in der
ein Drachenviereck ist
Zeige, dass das in der  Ebene liegende Viereck
Ebene liegende Viereck  ein Drachenviereck ist. Soll
ein Drachenviereck ist. Soll  ein Drachenviereck sein, so muss folgende Bedingung erfüllt werden:
ein Drachenviereck sein, so muss folgende Bedingung erfüllt werden:
 Berechne die Beträge der Strecken und begründe anhand des Resultats, dass bei
Berechne die Beträge der Strecken und begründe anhand des Resultats, dass bei  ein Drachenviereck vorliegt.
Aus dem Aufgabenteil zuvor weißt du, dass
ein Drachenviereck vorliegt.
Aus dem Aufgabenteil zuvor weißt du, dass  gilt.
gilt.

![\(\begin{array}{rll}
\mid \overrightarrow{AB} \mid&=&\left| \begin{pmatrix}
\sqrt{2}\\
1\\
0
\end{pmatrix} - \begin{pmatrix}
\sqrt{2}\\
0\\
0
\end{pmatrix} \right|\\[5pt]
&=& \left| \begin{pmatrix}
0\\
1\\
0
\end{pmatrix} \right|\\[5pt]
&=& \sqrt{0^2+1^2+0^2}\\[5pt]
&=&1\\\end{array}\)](https://www.schullv.de/resources/formulas/04e86fe2cb0f8da3a2bf9603cb8477a018532f94e06f985589ae29add5abf2ff_light.svg)
![\(\begin{array}{rll}
\mid \overrightarrow{DB} \mid&=& \left| \begin{pmatrix}
\sqrt{2}\\
1\\
0
\end{pmatrix} - \begin{pmatrix}
1\\
1\\
0
\end{pmatrix} \right|\\[5pt]
&=& \left| \begin{pmatrix}
\sqrt{2}-1\\
0\\
0
\end{pmatrix} \right|\\[5pt]
&=& \sqrt{\left(\sqrt{2}-1\right)^2+0^2+0^2}\\[5pt]
&=&\sqrt{2}-1\\
\end{array}\)](https://www.schullv.de/resources/formulas/c05ec5f32d4721ad625f41e7005b9d960b7362c5b2a5de658a23483688056e99_light.svg)
![\(\begin{array}{rll}
\mid \overrightarrow{DS} \mid&=& \left| \begin{pmatrix}
\frac{1}{2}\sqrt{2}\\
\frac{1}{2}\sqrt{2}\\
0
\end{pmatrix} - \begin{pmatrix}
1\\
1\\
0
\end{pmatrix} \right|\\[5pt]
&=& \left| \begin{pmatrix}
\frac{1}{2}\sqrt{2}-1\\
\frac{1}{2}\sqrt{2}-1\\
0
\end{pmatrix} \right|\\[5pt]
&=& \sqrt{\left(\frac{1}{2}\sqrt{2}-1\right)^2+\left(\frac{1}{2}\sqrt{2}-1\right)^2+0^2}\\[5pt]
&=&\sqrt{2}-1\\
\end{array}\)](https://www.schullv.de/resources/formulas/769f25b9ab9d15e052a610f2c6dc56b6e5d3be2ed359a7ae254c565fa122832f_light.svg) Damit hast du gezeigt, dass
Damit hast du gezeigt, dass  gilt und damit auch, dass es sich bei
gilt und damit auch, dass es sich bei  um ein Drachenviereck handelt.
um ein Drachenviereck handelt.
 Flächeninhalt des Vierecks
Flächeninhalt des Vierecks  bestimmen
Im Aufgabenteil zuvor hast du gezeigt, dass es sich bei
bestimmen
Im Aufgabenteil zuvor hast du gezeigt, dass es sich bei  um ein Drachenviereck handelt. Um nun den Flächeninhalt von
um ein Drachenviereck handelt. Um nun den Flächeninhalt von  zu bestimmen, kannst du die Formel für den Flächeninhalt
zu bestimmen, kannst du die Formel für den Flächeninhalt  eines Drachenvierecks verwenden:
eines Drachenvierecks verwenden:
 Bestimme die Beträge der Vektoren und setze diese in die oben genannte Formel ein, um den Flächeninhalt zu erhalten.
1. Schritt: Beträge der Vektoren bestimmen
Bestimme die Beträge der Vektoren und setze diese in die oben genannte Formel ein, um den Flächeninhalt zu erhalten.
1. Schritt: Beträge der Vektoren bestimmen
![\(\begin{array}{rll}
\left| \overrightarrow{AD} \right|&=& \left| \begin{pmatrix}
1\\
1\\
0
\end{pmatrix} - \begin{pmatrix}
\sqrt{2}\\
0\\
0
\end{pmatrix} \right|\\[5pt]
&=& \left| \begin{pmatrix}
1-\sqrt{2}\\
1\\
0
\end{pmatrix} \right|\\[5pt]
&=& \sqrt{(1-\sqrt{2})^2+1^2+0^2}\\[5pt]
&=&\sqrt{4-2 \cdot \sqrt{2}}\\
\end{array}\)](https://www.schullv.de/resources/formulas/c87bc77085726a6e0223bf17b70870b661a0639ed359addee27fe5f91bd4bc73_light.svg)
![\(\begin{array}{rll}
\mid \overrightarrow{SB} \mid&=& \left| \begin{pmatrix}
\sqrt{2}\\
1\\
0
\end{pmatrix} - \begin{pmatrix}
\frac{1}{2} \cdot \sqrt{2}\\
\frac{1}{2} \cdot \sqrt{2}\\
0
\end{pmatrix} \right|\\[5pt]
&=& \left| \begin{pmatrix}
\frac{1}{2} \cdot \sqrt{2}\\
1-\frac{1}{2} \cdot \sqrt{2}\\
0
\end{pmatrix} \right|\\[5pt]
&=& \sqrt{\left(\frac{1}{2} \cdot \sqrt{2}\right)^2+\left( 1-\frac{1}{2} \cdot \sqrt{2} \right)^2+0^2}\\[5pt]
&=&\sqrt{2-\sqrt{2}}\\
\end{array}\)](https://www.schullv.de/resources/formulas/a213a2a7e26af7722e0aa59a2b736ec9f647e4153f81b2b47de8580b2c2a44eb_light.svg) 2. Schritt: In Formel für Flächeninhalt einsetzen
Setze die berechneten Beträge in die oben genannte Formel ein:
2. Schritt: In Formel für Flächeninhalt einsetzen
Setze die berechneten Beträge in die oben genannte Formel ein:
 Der Flächeninhalt des Vierecks
Der Flächeninhalt des Vierecks  beträgt
beträgt  FE.
FE.