Wahlpflichtteil

Abbildung 1 zeigt den Graphen $G_f$ einer in $\mathbb{R}$ definierten Funktion $f.$

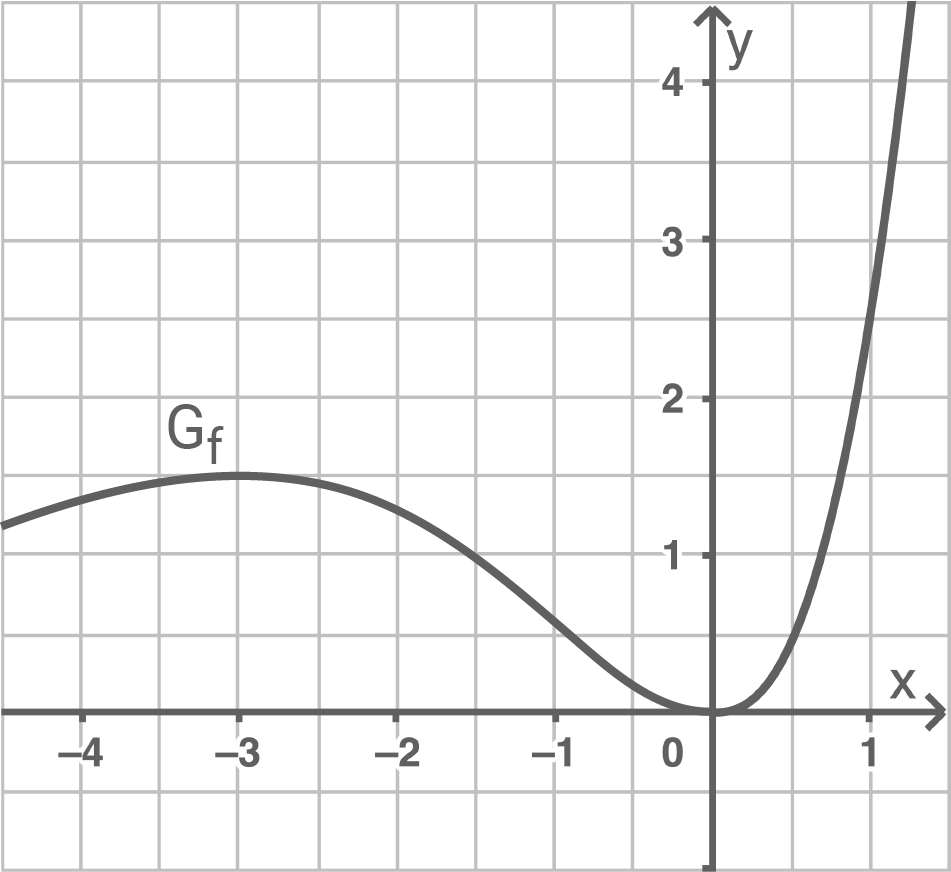
Graph Gf Integral Sachsen Anhalt Mathe Abi 2024

Abb. 1

(1)

Bestimme grafisch den Wert des Integrals $\displaystyle\int_{-3}^{-1,5}f(x)\;\mathrm dx.$

(2)

Beschreibe, wie der Graph der in $\mathbb{R}$ definierten Funktion $u$ mit $u(x)=-f(x)+2$ aus $G_f$ erzeugt werden kann.

Gib die Koordinaten des Hochpunkts des Graphen von $u$ an.

(2 + 3 Punkte)

Gegeben sind die in $\mathbb{R}$ definierten Funktionen $g$ mit $g(x)=2 \cdot \mathrm e^x-2$ und $h$ mit $h(x)= \mathrm e^x+1.$

Abbildung 2 zeigt ihre Graphen.

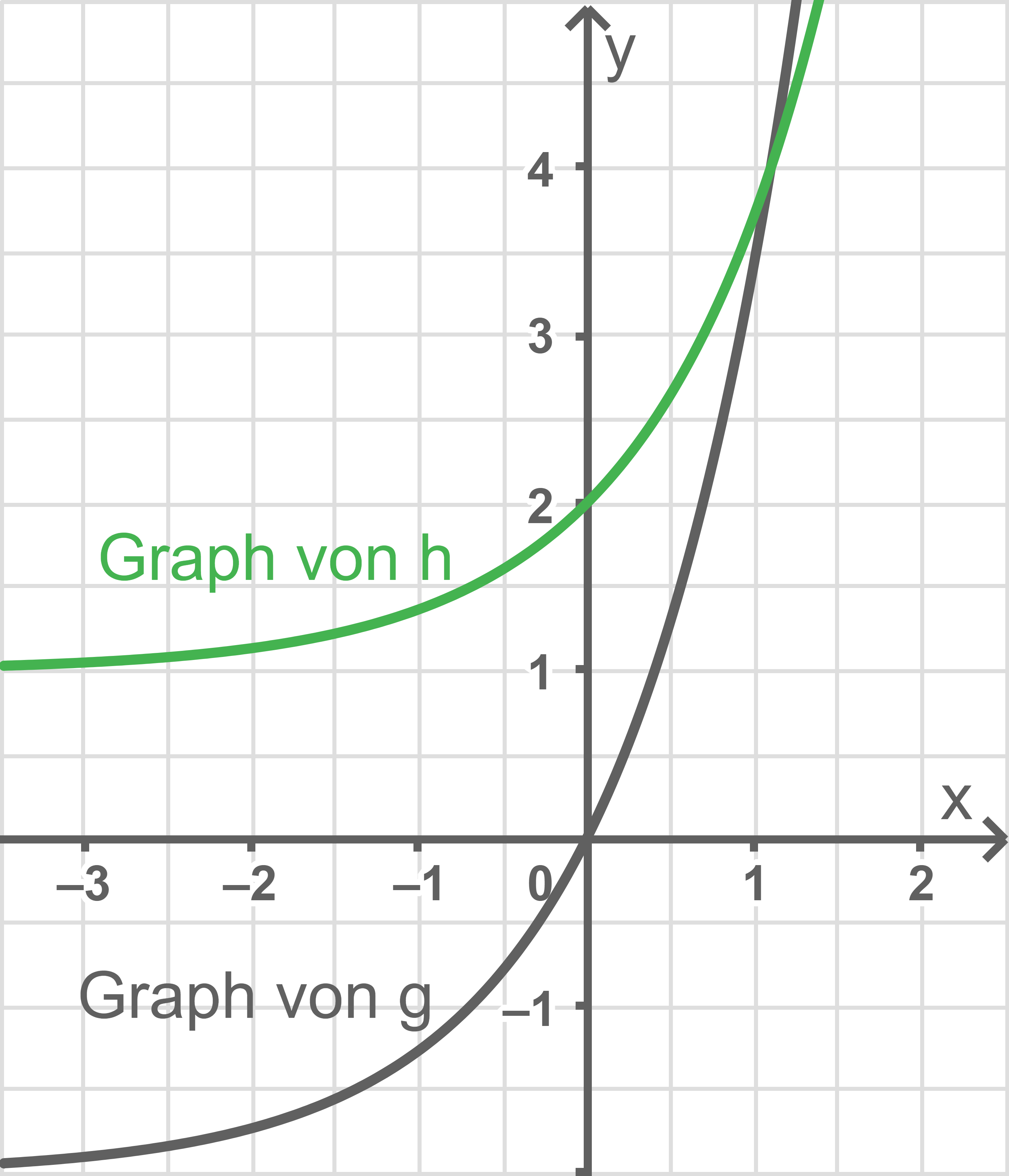
Abb. 2

(1)

Die erste Ableitungsfunktion von $g$ wird mit $\(g$ bezeichnet.

Berechne $\(g$ und veranschauliche in der Abbildung, wie man diesen Wert grafisch ermitteln kann.

(2)

Beurteile die folgende Aussage:

$\,$

Es gibt eine Verschiebung in $y$ -Richtung, durch die der Graph von $h$ aus dem Graphen von $g$ erzeugt werden kann.

(3 + 2 Punkte)

Gegeben sind der Punkt $P(0\mid0\mid3)$ sowie die Geraden $g: \overrightarrow{x}=\overrightarrow{O P}+t \cdot\pmatrix{2\\1\\-2},$ $t \in \mathbb{R},$ und $h: \overrightarrow{x}=\pmatrix{4\\2\\-1}+r \cdot\pmatrix{1\\0\\2},$ $r \in \mathbb{R}.$

(1)

Zeige, dass sich die Geraden $g$ und $h$ schneiden, und gib die Koordinaten des Schnittpunktes $S$ an.

(2)

Der Punkt $R(2\mid1\mid 1)$ liegt auf der Gerade $g.$

Bestimme die Koordinaten eines Punktes $\(P$ der auf der Gerade $g$ liegt und den gleichen Abstand vom Punkt $R$ hat wie der Punkt $P.$

(3 + 2 Punkte)

Die Punkte $A(1\mid 1\mid0),$ $B(4\mid 1\mid 0),$ $E(1\mid 1\mid4)$ und $H(1\mid 7 \mid 4)$ sind Eckpunkte des in Abbildung 3 dargestellten Quaders $ABCDEFGH.$

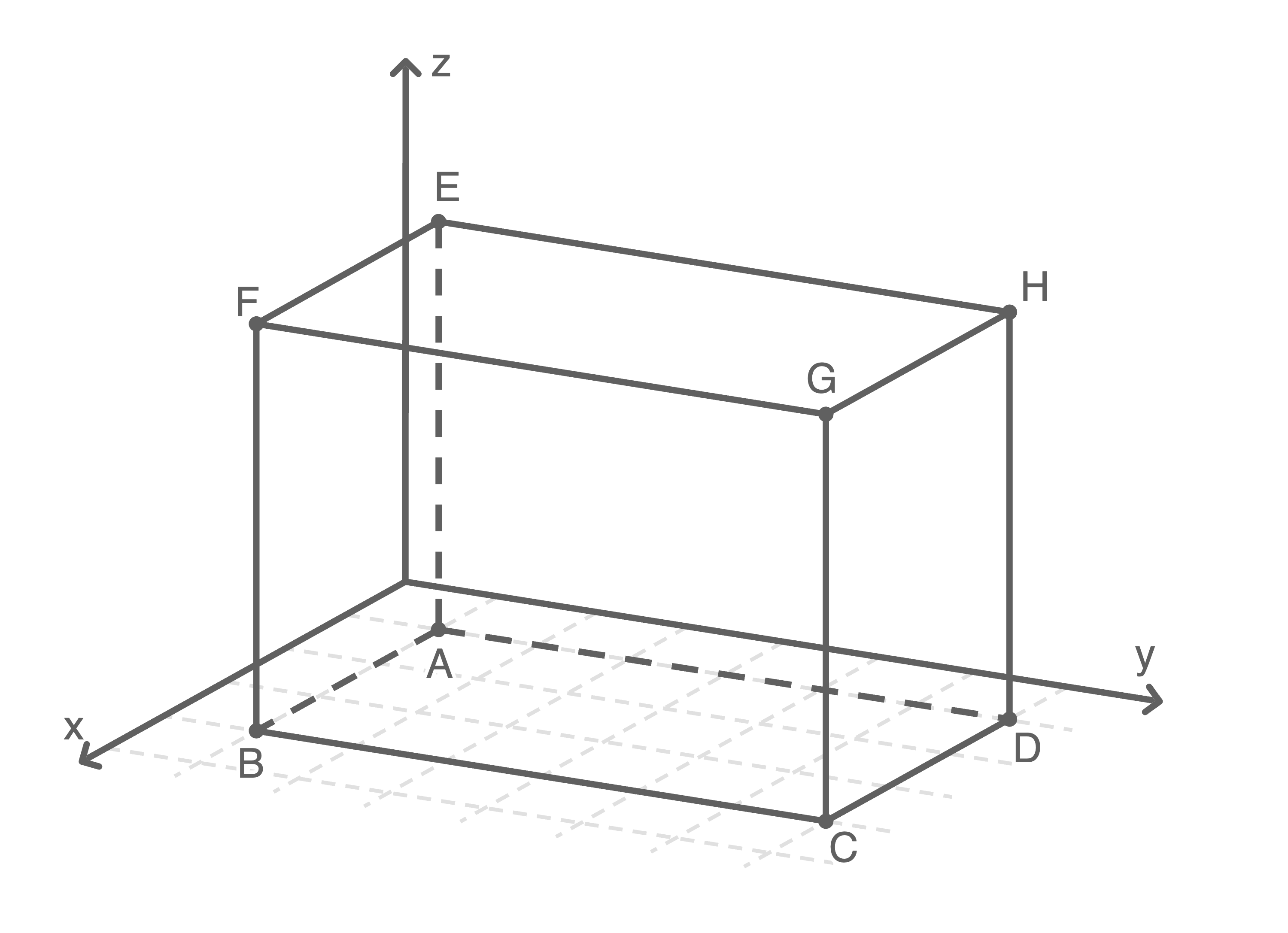
Quader Eckpunkte Sachsen Anhalt Mathe Abi 2024

Abb. 3

(1)

Gib die Koordinaten des Punktes $G$ an.

Der Quader wird parallel zu einer Gerade so verschoben, dass sich der Schnittpunkt seiner Raumdiagonalen im Koordinatenursprung befindet. Dabei entsteht der Quader $\(A$

(2)

Ermittle die Koordinaten des Punkts $\(H$

(3)

Gib einen Eckpunkt des Quaders $\(A$ an, der nur positive Koordinaten hat.

(1 + 3 + 1 Punkte)

In einem Spielwarengeschäft erhält jedes Kind im Rahmen einer Werbeaktion einen kleinen, blickdicht verpackten Ball. Die Wahrscheinlichkeit dafür, dass dieser Ball eine Glitzerfärbung hat, beträgt $40\,\%.$

(1)

Zeige, dass die Wahrscheinlichkeit dafür, dass in einer Gruppe von drei Kindern jedes Kind einen Ball mit Glitzerfärbung erhält, kleiner als $10\,\%$ ist.

(2)

Beschreibe im Sachzusammenhang ein Zufallsexperiment, bei dem die Wahrscheinlichkeit eines Ereignisses mit dem Term $\left(\frac{3}{5}\right)^4+4\cdot\left(\frac{3}{5}\right)^3\cdot\frac{2}{5}$ berechnet werden kann. Gib dieses Ereignis an.

(2 + 3 Punkte)

Die Zufallsgröße $X$ ist binomialverteilt mit den Parametern $n$ und $p=\frac{1}{4}.$

(1)

Für die Standardabweichung $\sigma$ von $X$ gilt: $\sigma=\sqrt{3}.$

Berechne $n.$

(2)

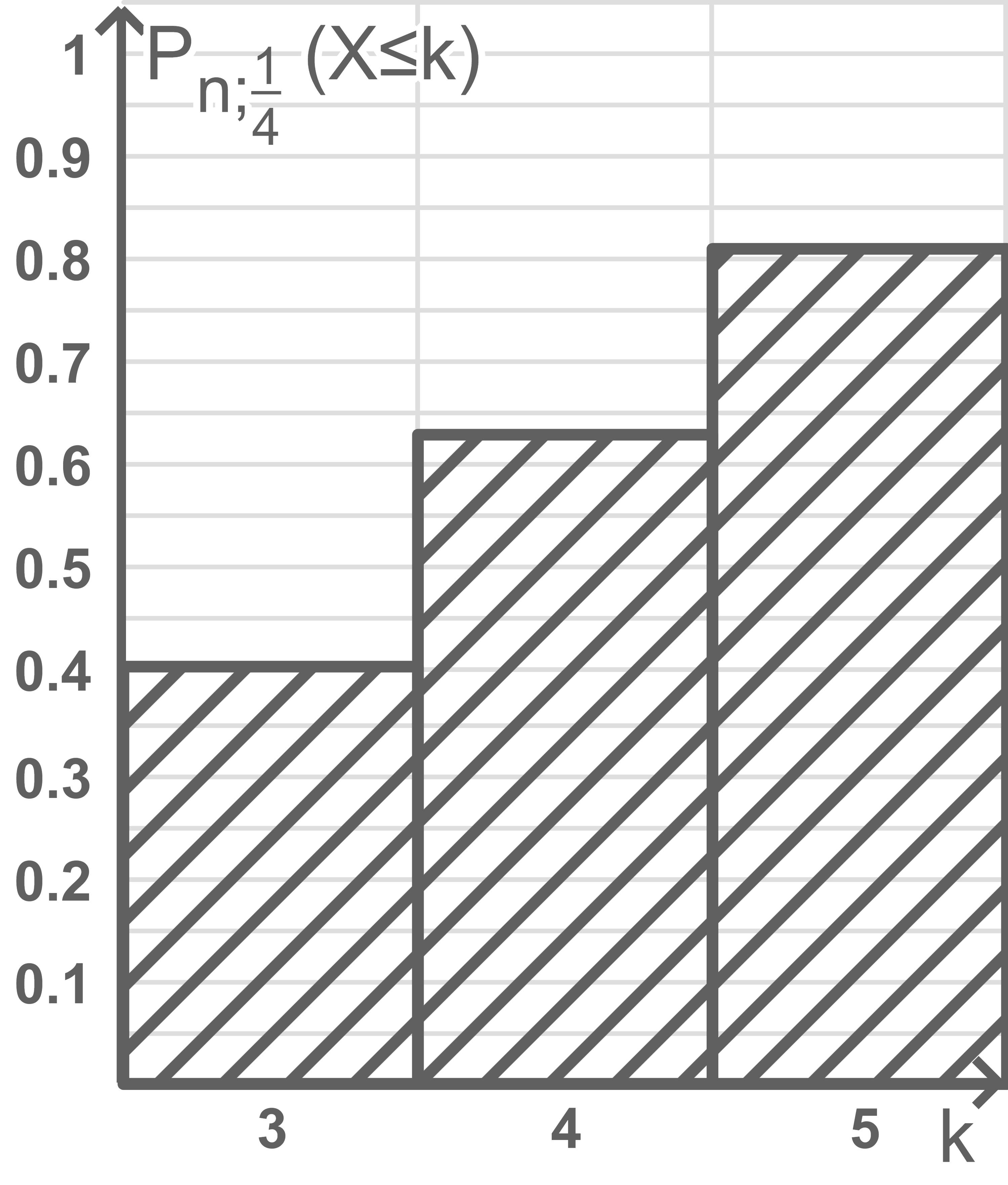
Die folgende Abbildung 4 zeigt die Werte $P_{n ; \frac{1}{4}}(X=k)$ der Zufallsgröße $X$ im Bereich von $k=3$ bis $k=5$ ; Abbildung 5 zeigt kumulierte Werte $P_{n ; \frac{1}{4}}(X \leq k)$ der Zufallsgröße $X$ im Bereich von $k=3$ bis $k=5.$

In Abbildung 5 fehlt der Wert $P_{n ; \frac{1}{4}}(X \leq 4).$

Abb. 4

Abb. 5

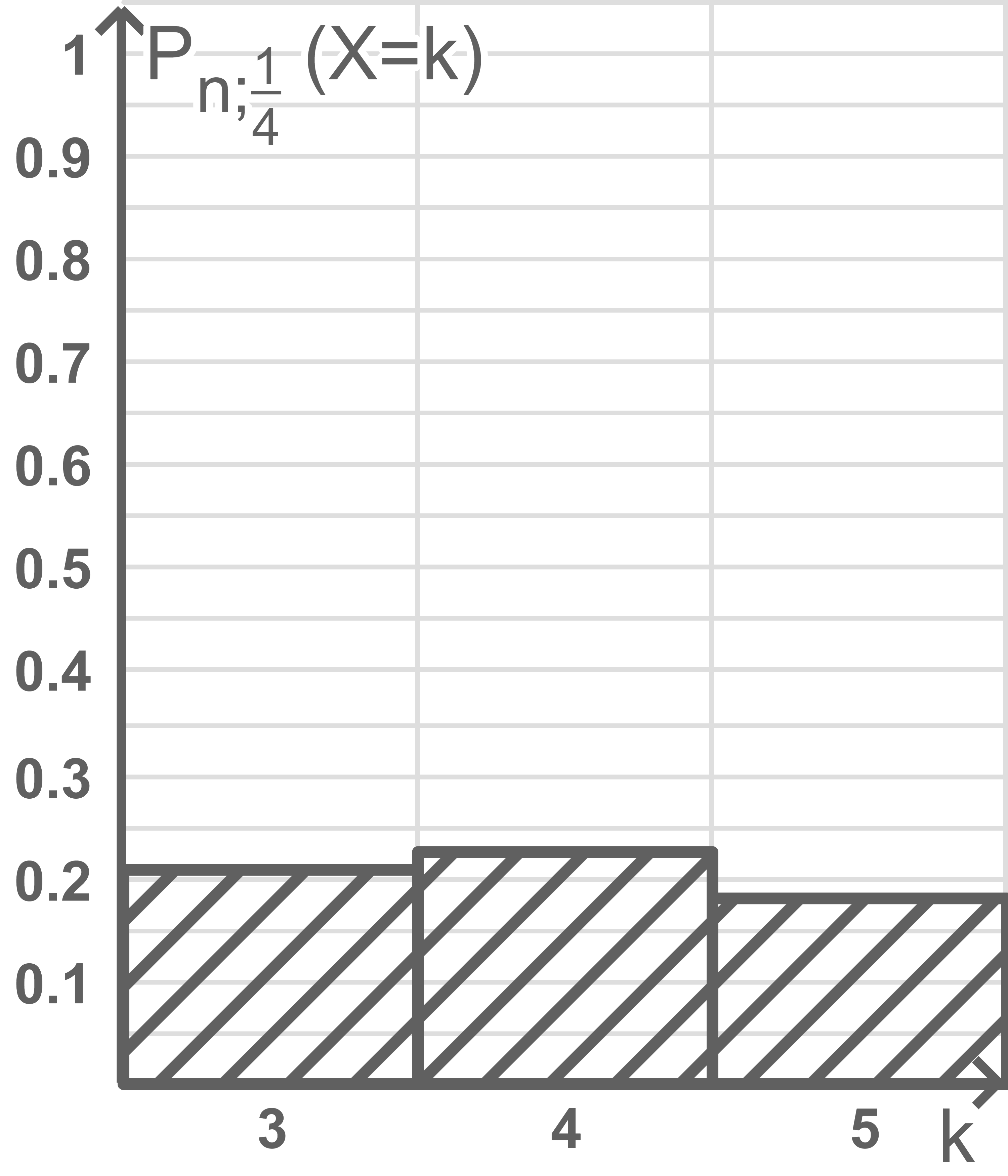
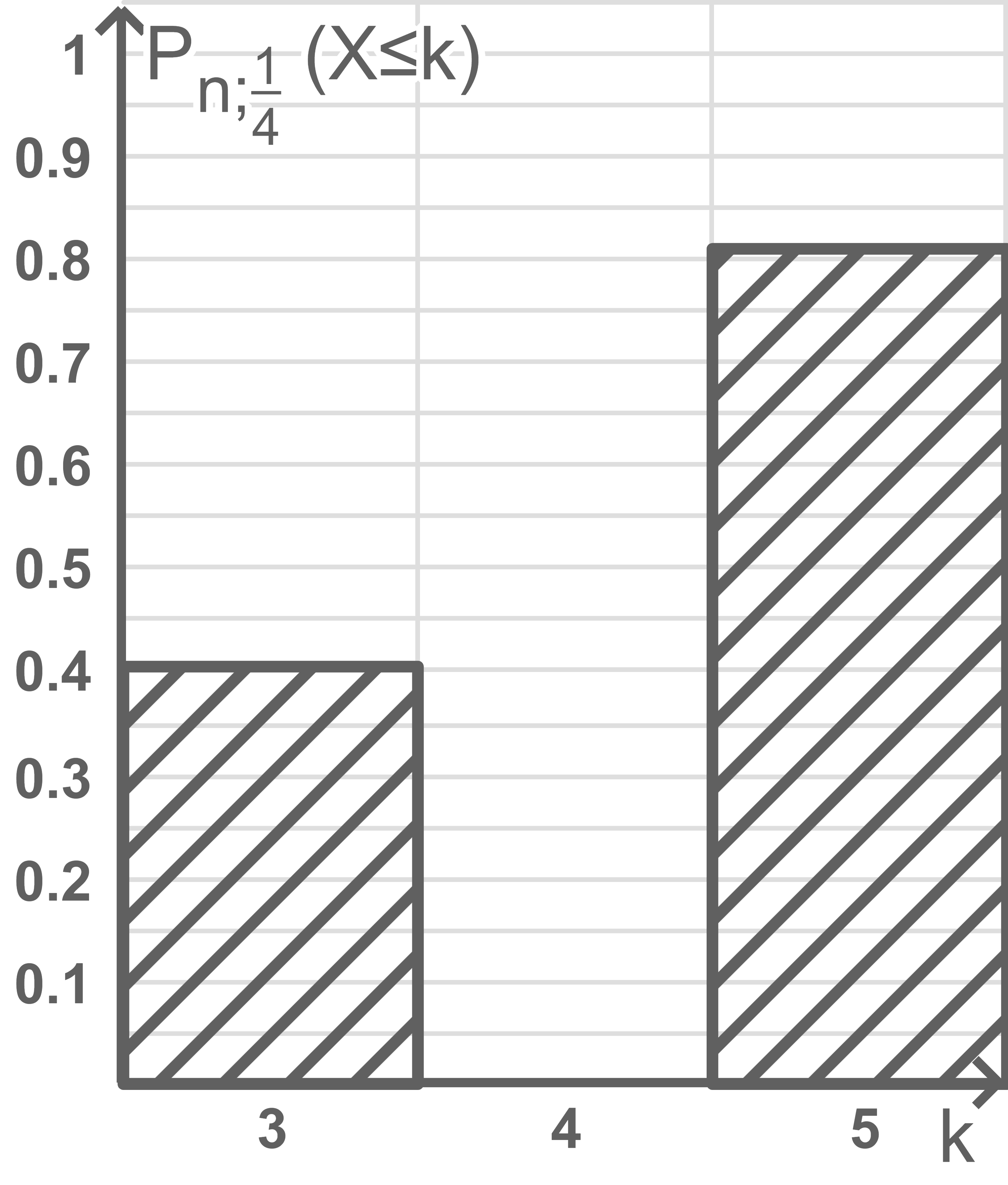Ermittle näherungsweise $P_{n ; \frac{1}{4}}(X \leq 4)$ und vervollständige Abbildung 5.

(2 + 3 Punkte)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

(1)

Der Wert des Integrals gibt den Inhalt der Fläche zwischen dem Graphen und der $x$ -Achse zwischen den beiden Grenzen an. Im betrachteten Bereich sind das ungefähr 8 Kästchen, das heißt der Wert des Integrals ist etwa $8\cdot0,5^2=2\;[\text{FE}].$

(2)

Erzeugung des Graphen beschreiben

Der Graph von $u$ kann aus $G_f$ durch Spiegelung an der $x$ -Achse und anschließende Verschiebung um $2$ in $y$ -Richtung erzeugt werden

Koordinaten des Hochpunkts angeben

Durch die Spiegelung an der $x$ -Achse wird aus dem Tiefpunkt von $G_f$ ein Hochpunkt. Die anschließende Verschiebung liefert somit die Koordinaten $H(0\mid 2)$ für den Hochpunkt des Graphen von $u.$

(1)

$\(\boldsymbol{g$ berechnen

Für die Ableitung von $g$ gilt:

$\(g$

Einsetzen von $x=0$ liefert:

$\(\begin{array}[t]{rll} g$

Grafische Ermittlung veranschaulichen

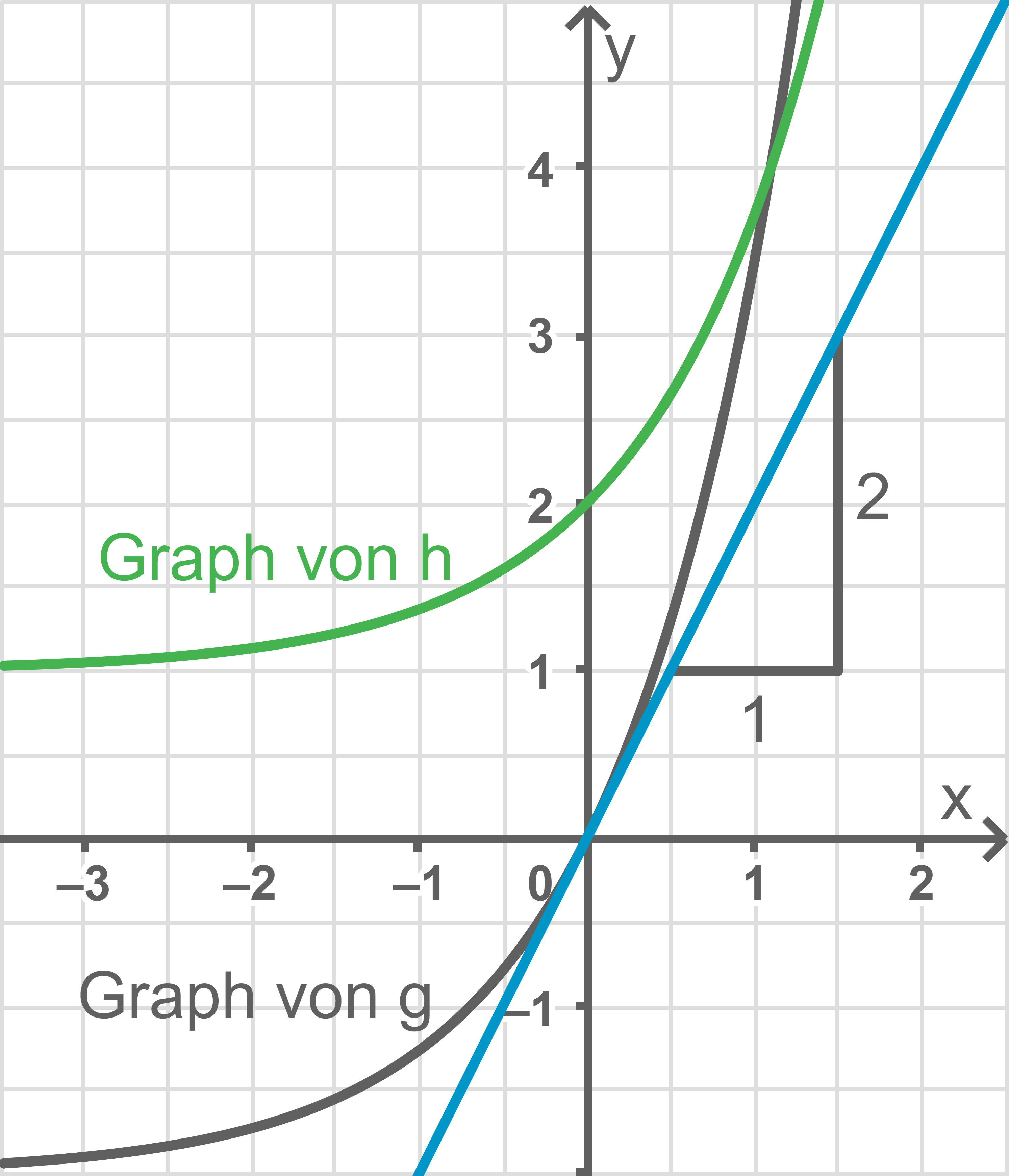
(2)

Die Aussage ist falsch, da aus der Abbildung deutlich hervorgeht, dass die Steigung der beiden Graphen an der Stelle $x=0$ nicht übereinstimmt.

(1)

Gleichsetzen der beiden Geradengleichungen liefert folgendes Gleichungssystem:

$\begin{array}{lrll} \text{I}\quad&2t&=& 4+r &\quad \scriptsize\mid\;\text{I}+\text{II}\\ \text{II}\quad&t&=& 2 &\quad \\ \text{III}\quad&3-2t&=& -1+2r &\quad \\ \end{array}$

Die zweite GLeichung liefert direkt $t=2.$ Einsetzen in Gleichung $\text{I}$ ergibt $4=4+r,$ das heißt $r=0.$ Einsetzen dieser beiden Werte in Gleichung $\text{III}$ ergibt $-1=-1.$ Somit hat das Gleichungssystem eine Lösung und die beiden Geraden schneiden sich. Einsetzen von $r=0$ in die Geradengleichung von $h$ liefert:

$\begin{array}[t]{rll} \overrightarrow{OS}&=&\pmatrix{4\\2\\-1}+0 \cdot\pmatrix{1\\0\\2} \\[5pt] &=&\pmatrix{4\\2\\-1} \end{array}$

Die Koordinaten von $S$ ergeben sich damit als $S(4\mid2\mid-1).$

(2)

Für den Vektor $\overrightarrow{PR}$ gilt:

$\begin{array}[t]{rll} \overrightarrow{PR}&=&\pmatrix{2\\1\\1}-\pmatrix{0\\0\\3} \\[5pt] &=&\pmatrix{2\\1\\-2} \end{array}$

Dieser Vektor entspricht dem Richtungsvektor der Geraden $g,$ d.h. für den Ortsvektor des Punkts $\(P$ folgt somit:

$\(\begin{array}[t]{rll} \overrightarrow{OP$

Der Punkt $\(P$ ist somit der Punkt $S$ und besitzt damit die Koordinaten $(4\mid2\mid-1).$

(1)

Der Punkt $G$ hat die gleichen $y$ - und $z$ -Koordinaten wie $H$ und die gleiche $x$ -Koordinate wie $B.$

Somit folgen die Koordinaten von $G$ mit $G(4 \mid 7 \mid 4).$

(2)

Die Raumdiagonalen des Quaders $ABCDEFGH$ schneiden sich genau in der Mitte des Quaders.

Eine Raumdiagonale des Quaders wird beispielsweise durch die Strecke $\overline{BH}$ dargestellt. Für den Mittelpunkt dieser Strecke gilt $M\left(\dfrac{x_B+x_H}{2} \,\bigg \vert \, \dfrac{y_B+y_H}{2} \,\bigg \vert \, \dfrac{z_B+z_H}{2} \right)$ und somit $M(2,5 \mid 4 \mid 2).$

Für $\(H$ gilt also:

$\(\overrightarrow{OH$

Die Koordinaten des Punkts $\(H$ sind somit gegeben durch $\(H$

(3)

Ein Eckpunkt des neuen Quaders $\(A$ der nur positive Koordinaten hat, ist $\(G$

Es gilt:

$\(\overrightarrow{OG$

(1)

$0,4^3=0,064\lt0,1$

(2)

Ein mögliches Zufallsexperiment wäre, dass vier Kinder jeweils einen Ball bekommen. Das Ereignis, dessen Wahrscheinlichkeit durch den Term beschrieben wird, ist, dass mindestens drei von den vier Bällen keine Glitzerfärbung haben.

(1)

$\begin{array}[t]{rll} \sigma&=&\sqrt{3} \\[5pt] \sqrt{n\cdot p\cdot(1-p)}&=&\sqrt{3} &\quad \scriptsize \mid\;()^2 \\[5pt] n\cdot \dfrac{1}{4}\cdot\left(1-\dfrac{1}{4}\right)&=&3 \\[5pt] \dfrac{3}{16}n&=&3 &\quad \scriptsize \mid\;\cdot\frac{16}{3} \\[5pt] n&=&16 \end{array}$

(2)

Aus den Abbildungen folgt näherungsweise $P_{n;\frac{1}{4}}(X\leq3)=0,4$ und $P_{n;\frac{1}{4}}(X=4)\approx0,23.$ Damit ergibt sich $P_{n;\frac{1}{4}}(X\leq4)\approx0,4+0,23=0,63.$ Für die vervollständigte Abbildung folgt somit:

Grafik zur Darstellung der Wahrscheinlichkeit Pn;1/4 für Werte von X bis k.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?