Aufgabe 4

Aufgabenstellung

Biologen wollen die Entwicklung einer Mäusebussardpopulation in einem Untersuchungsgebiet durch eine Matrix beschreiben. Dabei werden (auch in der gesamten folgenden Aufgabe) ausschließlich die weiblichen Tiere der Population betrachtet. Die Bussardpopulation besteht aus Küken ( $k$ ), Jungvögeln ( $j$ ), die noch nicht geschlechtsreif sind, und Altvögeln ( $a$ ), die fortpflanzungsfähig sind. Die Küken entwickeln sich im Jahr nach dem Schlüpfen zu Jungvögeln und nach einem weiteren Jahr zu Altvögeln.
Nach Beobachtungen des Bestandes der Bussarde wurde vor ca. $25$ Jahren zur Modellierung der Populationsentwicklung die Matrix

		von:	$k$	$j$	$a$
	$k$		$\begin{pmatrix}0&0&0,6\\[2pt]0,5&0&0\\[2pt]0&0,7&0,79\end{pmatrix}$
nach:	$j$	$A=$
	$a$

erstellt.

(1)

Stelle die Entwicklung der Bussardpopulation nach dem vorgeschlagenen Modell durch einen Übergangsgraphen dar und interpretiere die Bedeutung der Matrixeinträge $0,6$ und $0,79$ im Sachzusammenhang.

(8P)

(2)

Zur Simulation der Entwicklung der Population wurde von einem Bestand von $30$ Küken, $30$ Jungvögeln und $30$ Altvögeln ausgegangen.
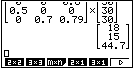
Berechne die Verteilung auf die drei Altersstufen in der Population für das nächste und das übernächste Jahr.

(4P)

(3)

Berechne den Anteil der gerade geschlüpften Küken, die bei einer Modellierung mit der Matrix $A$ drei Jahre später noch leben.

(3P)

In einem Jahr wurden $60$ Küken, $20$ Jungvögel und $100$ Altvögel im Beobachtungsgebiet gezählt.
Ermittle die Anzahlen an Küken, Jungvögeln und Altvögeln im Beobachtungsgebiet im Jahr zuvor, wenn die angegebene Modellierung der Populationsentwicklung durch die Matrix $A$ vorausgesetzt wird.

(5P)

(1)

Bestimme $x$ und $y$ so, dass $A \cdot \pmatrix{x \\ 9 \\ 30} = y \cdot \pmatrix{x \\ 9 \\ 30}$ gilt.
[Zur Kontrolle: $x=18$ und $y=1$ .]

(6P)

(2)

Interpretiere den Sachverhalt aus c) (1) im Kontext.

(3P)

Veränderte Umweltbedingungen führen heute dazu, dass zur Modellierung jetzt die Matrix $B$ gewählt wird:

$B=\begin{pmatrix}0&0&0,7\\[2pt]0,6&0&0\\[2pt]0&0,75&0,8\end{pmatrix}$ .

(1)

Vergleiche die Matrizen $A$ und $B$ im Sachzusammenhang.

Es ist $B^3=\begin{pmatrix}0,315&0,42&0,448\\[2pt]0&0,315&0,336\\[2pt]0,36&0,48&0,827\end{pmatrix}$ .

(3P)

(2)

Für eine Population wird vorausgesetzt, dass zu einem bestimmten Zeitpunkt die Anzahlen von Küken, Jungvögeln und Altvögeln übereinstimmen. Eine Forschungsgruppe behauptet, dass in diesem Fall die Gesamtzahl der Tiere nach der Modellierung in einem Zeitraum von $3$ Jahren um $20$ $\%$ zunimmt.
Beurteile die Aussage.

(7P)

(3)

Untersuche, bei welcher Überlebensrate $u$ der Altvögel in der Matrix $B_u=\begin{pmatrix}0&0&0,7\\[2pt]0,6&0&0\\[2pt]0&0,75&u\end{pmatrix}$ es nach der Modellierung eine von $\pmatrix{0 \\ 0 \\ 0}$ verschiedene Verteilung auf die drei Entwicklungsstufen der Bussardpopulation gibt, die im folgenden Jahr wieder zu derselben Verteilung führt.

(7P)

Zurzeit lebt in einem Beobachtungsgebiet eine Population, bei der sich die Anzahlen von Küken, Jungvögeln und Altvögeln von Jahr zu Jahr nicht verändern. In der Population leben $50$ Altvögel.

(4)

Bestimme die Anzahlen von Küken und Jungvögeln, wenn zur Modellierung der Population die Matrix $B_{0,685}=\begin{pmatrix}0&0&0,7\\[2pt]0,6&0&0\\[2pt]0&0,75&0,685\end{pmatrix}$ gewählt wird.

(4P)

(1)

$\blacktriangleright$ Übergangsgraph zeichnen

Du sollst die vorgestellte Entwicklung der Bussardpopulation in einem Übergangsgraph darstellen. Dem Aufgabentext kannst du entnehmen, dass es drei Entwicklungsstadien gibt: $k$ , $j$ und $a$ . Die entsprechenden Übergangswahrscheinlichkeiten kannst du der Matrix $A$ entnehmen. Dann erhältst du ein ähnliches Schaubild wie das folgende:

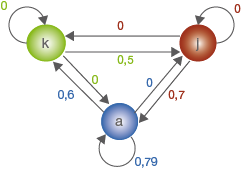Diagramm mit drei Knoten und gerichteten Kanten, beschriftet mit Zahlen.

Abb. 1: Übergangsgraph

$\blacktriangleright$ Bedeutung der Matrixeinträge interpretieren

Du sollst die Einträge $0,6$ und $0,79$ der Matrix $A$ im Sachzusammenhang interpretieren. Beachte dabei, dass der Eintrag $a_{ij}$ einer Übergangsmatrix die Übergangsrate vom Zustand $j$ in den Zustand $i$ beschreibt.

In diesem Fall befindet sich der Eintrag $0,6$ in der ersten Zeile der dritten Spalte und beschreibt daher die durchschnittliche Anzahl an Küken, die jährlich von einem ausgewachsenen weiblichen Tier ausgebrütet werden.
Der Eintrag $0,79$ befindet sich in der dritten Zeile der dritten Spalte. Er beschreibt demnach die Übergangsrate von den ausgewachsenen Tieren zu den ausgewachsenen Tieren, also die Überlebensrate der fortpflanzungsfähigen ausgewachsenen weiblichen Tiere.

(2)

$\blacktriangleright$ Verteilungen für die Folgejahre berechnen

Du sollst die Verteilungen der Bussardpopulation der nächsten beiden Jahre berechnen. Den Verteilungsvektor $\overrightarrow{v}_t$ , der die Verteilung zum Zeitpunkt $t$ beschreibt, kannst du mit Hilfe der zugehörigen Übergangsmatrix $A$ wie folgt berechnen:

$\overrightarrow{v}_t = M \cdot \overrightarrow{v}_{t-1} = M^t \overrightarrow{v}_0$

Gesucht sind hier $\overrightarrow{v}_1$ und $\overrightarrow{v}_2$ . $\overrightarrow{v}_0$ kannst du der Aufgabenstellung entnehmen:

$\overrightarrow{v}_0 = \begin{pmatrix}30\\30\\30 \end{pmatrix}$

Du kannst nun die gesuchten Vektoren entweder handschriftlich oder mit deinem GTR berechnen.

$\blacktriangleright$ Lösungsweg A: Handschriftlich

Einsetzen in die Formel liefert:

$\overrightarrow{v}_1 = \begin{pmatrix} 18 \\ 15\\ 44,7\end{pmatrix}$

Vollständige Lösung anzeigen

$\overrightarrow{v}_2 =\begin{pmatrix} 26,82 \\ 9\\ 45,813\end{pmatrix}$

Vollständige Lösung anzeigen

$\blacktriangleright$ Lösungsweg B: GTR

Eine Matrix kannst du über folgende Befehlsfolge eingeben:

2nd $\to$ $x^{-1}$ (MATRIX) $\to$ EDIT

Die eingegebenen Matrizen und Vektoren kannst du dann über folgenden Befehl wieder abrufen, um mit ihnen zu rechnen:

2nd $\to$ $x^{-1}$ (MATRIX) $\to$ NAMES

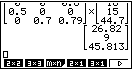
Du erhältst dann folgende Ergebnisse:

$\overrightarrow{v}_1 = A\cdot \overrightarrow{v}_0 = \begin{pmatrix} 18 \\ 15\\ 44,7\end{pmatrix}$

$\overrightarrow{v}_2 = A\cdot \overrightarrow{v}_1 = \begin{pmatrix} 26,82 \\ 9\\ 45,813\end{pmatrix}$

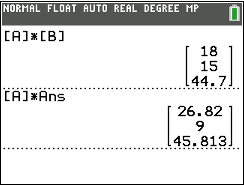Bildschirmansicht eines Taschenrechners mit mathematischen Berechnungen und Ergebnissen.

Abb. 2: Verteilungsvektoren

Im nächsten Jahr besteht die Population nach dem Modell aus $18$ Küken, $15$ Jungvögeln und ca. $45$ fortpflanzungsfähigen Altvögeln. Im darauffolgenden Jahr gibt es ca. $27$ Küken, $9$ Jungvögel und ca. $46$ Altvögel.

(3)

$\blacktriangleright$ Überlebensrate der Küken berechnen

Gesucht ist der Anteil der Küken, die drei Jahre nach dem Schlüpfen noch leben. Die Wahrscheinlichkeit dafür, dass ein geschlüpftes Küken im nächsten Jahr noch lebt ist gerade die Übergangsrate der Küken zu den Jungvögeln, also $0,5$ . Da die Küken dann zu den Jungvögeln gehören, muss für das zweite Jahr die Überlebensrate dieser betrachtet werden, $0,7$ . Für das dritte Jahr zählt die Überlebensrate der Altvögel, also $0,79$ . Mit der Pfadmultiplikationsregel kannst du nun den gesuchten Anteil $p_3$ berechnen:

$\begin{array}[t]{rll} p_3&=& 0,5\cdot 0,7\cdot 0,79 \\[5pt] &=&\dfrac{553}{2.000} \\[5pt] &=& 0,2765 \\[5pt] &=& 27,65\,\% \end{array}$

Drei Jahre nach dem Schlüpfen leben ca. $27,65\,\%$ der Küken noch.

$\blacktriangleright$ Verteilung des Vorjahres ermitteln

Zum Zeitpunkt $t$ gibt es $60$ Küken, $20$ Jungvögel und $100$ Altvögel. Du sollst nun berechnen, wie viele Vögel es in den einzelnen Entwicklungsstadien im Jahr davor, also zur Zeit $t-1$ , gab. Diesmal hast du also $\overrightarrow{v}_t$ gegeben und suchst $\overrightarrow{v}_{t-1}$ . Nutze die Formel aus a) (2), um eine Gleichung aufzustellen. Mit $\overrightarrow{v}_{t-1} = \begin{pmatrix} x\\y\\z\end{pmatrix}$ erhältst du daraus ein lineares Gleichungssystem, das du nach $x$ , $y$ und $z$ lösen kannst.

$\overrightarrow{v}_t$ kannst du aus der Aufgabenstellung ablesen:

$\overrightarrow{v}_t = \begin{pmatrix}60 \\ 20 \\ 100 \end{pmatrix}$

Du erhältst folgende Gleichung:

$...=\begin{pmatrix}60 \\ 20 \\ 100 \end{pmatrix}$

Vollständige Lösung anzeigen

Daraus ergibt sich folgendes Gleichungssystem:

$\begin{array}{} \text{I}\quad&60&=& \quad 0,6z\\ \text{II}\quad&20&=& \quad 0,5x\\ \text{III}\quad&100&=& \quad 0,7y+0,79z\\ \end{array}$

Aus $\text{I}$ kannst du direkt eine Lösung für $z$ bestimmen:

$\begin{array}[t]{rll} 60&=& 0,6z &\quad \scriptsize \mid\; :0,6 \\[5pt] 100&=& z \\[5pt] \end{array}$

Aus $\text{II}$ kannst du eine Lösung für $x$ bestimmen:

$\begin{array}[t]{rll} 20&=& 0,5x &\quad \scriptsize \mid\; :0,5 \\[5pt] 40&=& x \\[5pt] \end{array}$

Die Lösung für $z$ kannst du nun in $\text{III}$ einsetzen und erhältst dann eine Lösung für $y$ :

$\begin{array}[t]{rll} 100&=& 0,7y +0,79z &\quad \scriptsize \mid\; z = 100 \\[5pt] 100&=&0,7y+79 &\quad \scriptsize \mid\;-79 \\[5pt] 21&=&0,7y &\quad \scriptsize \mid\;: 0,7 \\[5pt] 30&=& y \\[5pt] \end{array}$

Im Jahr zuvor gab es nach der Modellierung durch die Matrix $A$ $40$ Küken, $30$ Jungvögel und $100$ Altvögel.

(1)

$\blacktriangleright$ $\boldsymbol{x}$ und $\boldsymbol{y}$ bestimmen

Du sollst $x$ und $y$ so bestimmen, dass folgende Gleichung erfüllt ist:

$A \cdot \begin{pmatrix}x\\ 9 \\ 30 \end{pmatrix} = y \cdot \begin{pmatrix}x\\9\\30 \end{pmatrix}$

Setzt du dort $A$ ein, kannst du ein Gleichungssystem aufstellen, das du nach $x$ und $y$ lösen kannst.

$\begin{pmatrix} 0,6\cdot 30 \\ 0,5x\\ 0,7\cdot 9 + 0,79\cdot 30\end{pmatrix}=\begin{pmatrix}xy\\9y\\30y\end{pmatrix}$

Vollständige Lösung anzeigen

Du erhältst folgendes Gleichungssystem:

$\begin{array}{} \text{I}\quad&18&=& xy\quad \\ \text{II}\quad&0,5x&=&9y\quad\\ \text{III}\quad&30&=&30y\quad\\ \end{array}$

Aus der dritten Gleichung erhältst du direkt:

$\begin{array}[t]{rll} 30&=& 30y&\quad \scriptsize \mid\;:30 \\[5pt] 1&=& y \end{array}$

Dies kannst du nun in $\text{I}$ einsetzen und erhältst:

$18 = x\cdot y =x\cdot 1 = x$

Zur Kontrolle kannst du nun deine Ergebnisse noch in $\text{II}$ einsetzen:

$\begin{array}[t]{rll} 0,5x&=& 9y \\[5pt] 0,5 \cdot 18&=&9\cdot 1 \\[5pt] 9&=&9\\[5pt] \end{array}$

Grünes Häkchen-Symbol auf transparentem Hintergrund.

Für $x = 18$ und $y= 1$ ist die gegebene Gleichung erfüllt.

(2)

$\blacktriangleright$ Sachverhalt interpretieren

Um den Sachverhalt aus c) (1) im Kontext zu interpretieren, betrachte die Gleichung genauer und überlege, was die Einträge der Vektoren im Sachzusammenhang bedeuten. Wichtig ist, dass beide Vektoren in der Gleichung identisch sind.

Die Gleichung bedeutet, dass sich die Population mit $x$ Küken, $9$ Jungvögeln und $30$ Altvögeln im nächsten Jahr um den Faktor $y$ vervielfacht, wobei sich die Anzahl der einzelnen Entwicklungsstufen mit $y$ multipliziert und nicht nur die Gesamtanzahl.

Da diese Gleichung nur ein Lösungspaar besitzt, gibt es nur eine Anzahl von Küken, für die dies möglich ist. Insbesondere ist hier $y =1$ , die Anzahl der Vögel in den einzelnen Entwicklungsstadien bleibt bei dieser Verteilung also über die Jahre gleich.

(1)

$\blacktriangleright$ Matrizen im Sachzusammenhang vergleichen

Du sollst die Matrizen $A$ und $B$ im Sachzusammenhang vergleichen:

$A = \begin{pmatrix}0 & 0 & 0,6 \\ 0,5 & 0 & 0 \\ 0 & 0,7 & 0,79 \end{pmatrix}\quad$

$\quad B = \begin{pmatrix}0 & 0& 0,7 \\ 0,6 & 0 & 0 \\ 0 & 0,75 & 0,8 \end{pmatrix}$

Die Elemente, die schon in $A$ Null waren, sind auch in $B$ Null. Vergleiche also die von Null verschiedenen Einträge.

Alle von Null verschiedenen Einträge sind in der Matrix $B$ größer als in $A$ . Diese Einträge beschreiben die Überlebensraten in den einzelnen Entwicklungsstadien, bzw. die Anzahl an Nachkommen pro fortpflanzungsfähigem Weibchen. Die Population im neuen Model wächst also stärker als im alten Modell.

(2)

$\blacktriangleright$ Aussage beurteilen

Es soll einen Zeitpunkt geben, bei dem die Anzahlen der Küken, Jungvögel und Altvögel übereinstimmen. Für diesen Bestand sollst du dann die Entwicklung des Bestands drei Jahre später betrachten. Für den Bestand mit identischen Anzahlen, kannst du folgenden Verteilungsvektor verwenden:

$\overrightarrow{w}_0 = \begin{pmatrix}w\\w\\w\end{pmatrix}$

Berechne nun die Gesamtanzahl der Tiere nach drei Jahren und fasse den Term so weit wie möglich zusammen. Dadurch kannst du eine Aussage über die prozentuale Zunahme treffen. Die Matrix $B^3$ ist dir in der Aufgabenstellung gegeben. Du kannst hier also einfach die zweite Variante der Formel aus a) anwenden:

$\overrightarrow{w}_3 = B^3 \cdot \overrightarrow{w}_0 =\begin{pmatrix}1,183w\\ 0,651w\\ 1,667w \end{pmatrix}$

Vollständige Lösung anzeigen

Die Gesamtanzahl der Vögel der Population $w_t$ ergibt sich dann wie folgt:

$w_0 = 3w$

$w_3 = 3,501w$

Vollständige Lösung anzeigen

Es ergibt sich also:

$\dfrac{w_3}{w_0}= \dfrac{3,501w}{3w}= 1,167$

Die Gesamtanzahl der Tiere nimmt nur um $16,7\,\%$ zu, also ist die Aussage der Forschungsgruppe falsch.

(3)

$\blacktriangleright$ Überlebensrate untersuchen

Du sollst überprüfen, für welche Überlebensrate $u$ sich eine stabile Population einstellt. Gesucht ist also $u$ , sodass es eine Verteilung $\overrightarrow{s} \neq \overrightarrow{0}$ gibt, die folgende Gleichung erfüllt:

$B_u \cdot \overrightarrow{s} = \overrightarrow{s}$

Stelle also für $\overrightarrow{s} = \begin{pmatrix}s_1 \\s_2\\s_3 \end{pmatrix}$ diese Gleichung auf. Daraus erhältst du wieder ein Gleichungssystem, bei dem eine Gleichung von $u$ abhängt. Aus dieser kannst du mit Hilfe der übrigen Gleichungen eine Aussage über $u$ gewinnen.

$B_u \cdot \overrightarrow{s} = \overrightarrow{s}$

Vollständige Lösung anzeigen

Du erhältst also folgendes Gleichungssystem:

$\begin{array}{} \text{I}\quad&s_1&=& \quad 0,7s_3\\ \text{II}\quad&s_2&=& \quad 0,6s_1\\ \text{III}\quad&s_3&=&\quad 0,75s_2 + us_3\\ \end{array}$

Setze nun nacheinander erst $\text{I}$ in $\text{II}$ und dies dann wiederum in $\text{III}$ ein, damit $\text{III}$ nur noch von $s_3$ und $u$ abhängt:

$s_2 = 0,42s_3\quad$ $(-0,685+u)s_3 = 0$

Vollständige Lösung anzeigen

Diese Gleichung ist wegen des Satzes vom Nullprodukt erfüllt, wenn $s_3 =0$ oder $-0,685+u =0$ gilt. Wenn aber $s_3 = 0$ wäre, dann wären auch $s_1 =s_2 =0$ , was in der Aufgabenstellung ausgeschlossen ist. Also muss $-0,685+u =0$ sein. Löse dies nun nach $u$ auf:

$\begin{array}[t]{rll} -0,685+u&=& 0&\quad \scriptsize \mid\; +0,685 \\[5pt] u&=&0,685 \\[5pt] \end{array}$

Bei einer Überlebensrate von $u = 0,685 = 68,5\,\%$ gibt es eine von Null verschiedene Verteilung, die sich im nächsten Jahr wieder ergibt.

(4)

$\blacktriangleright$ Anzahlen bestimmen

Gegeben hast du die Matrix $B_{0,685}$ . Dir sollte auffallen, dass dies genau die Matrix $B_u$ mit dem Wert $u$ ist, den du oben berechnet hast. Gesucht ist jetzt $\overrightarrow{s}$ , wobei die Anzahl der Altvögel als $s_3 = 50$ in der Aufgabenstellung vorgegeben ist. Nutze das Gleichungssystem von oben, um daraus die Anzahlen $s_1$ und $s_2$ zu berechnen:

$\begin{array}[t]{rll} s_2&=& 0,42s_3 \\[5pt] &=&0,42\cdot 50 \\[5pt] &=& 21 \\[10pt] s_1&=&0,7s_3 \\[5pt] &=& 0,7\cdot 50 \\[5pt] &=& 35 \\[5pt] \end{array}$

In der Population, die jedes Jahr gleich bleibt, gibt es neben den $50$ Altvögeln $35$ Küken und $21$ Jungvögel.

Bildnachweise [nach oben]

[1]

[2]

(1)

$\blacktriangleright$ Übergangsgraph zeichnen

Abb. 1: Übergangsgraph

$\blacktriangleright$ Bedeutung der Matrixeinträge interpretieren

(2)

$\blacktriangleright$ Verteilungen für die Folgejahre berechnen

$\overrightarrow{v}_t = M \cdot \overrightarrow{v}_{t-1} = M^t \overrightarrow{v}_0$

Gesucht sind hier $\overrightarrow{v}_1$ und $\overrightarrow{v}_2$ . $\overrightarrow{v}_0$ kannst du der Aufgabenstellung entnehmen:

$\overrightarrow{v}_0 = \begin{pmatrix}30\\30\\30 \end{pmatrix}$

Du kannst nun die gesuchten Vektoren entweder handschriftlich oder mit deinem GTR berechnen.

$\blacktriangleright$ Lösungsweg A: Handschriftlich

Einsetzen in die Formel liefert:

$\overrightarrow{v}_1 = \begin{pmatrix} 18 \\ 15\\ 44,7\end{pmatrix}$

Vollständige Lösung anzeigen

$\overrightarrow{v}_2 =\begin{pmatrix} 26,82 \\ 9\\ 45,813\end{pmatrix}$

Vollständige Lösung anzeigen

$\blacktriangleright$ Lösungsweg B: GTR

Eine Matrix kannst du über folgende Befehlsfolge eingeben:

F4 (MATH) $\to$ F1 (MAT)

Dort musst du noch die entsprechende Dimension auswählen bzw. eingeben.

Du erhältst dann folgende Ergebnisse:

$\overrightarrow{v}_1 = A\cdot \overrightarrow{v}_0 = \begin{pmatrix} 18 \\ 15\\ 44,7\end{pmatrix}$

$\overrightarrow{v}_2 = A\cdot \overrightarrow{v}_1 = \begin{pmatrix} 26,82 \\ 9\\ 45,813\end{pmatrix}$

Bildschirmansicht einer mathematischen Berechnung mit Matrizen.

Abb. 2: Verteilungsvektor $\overrightarrow{v}_1$

Mathematische Berechnung auf einem Taschenrechner mit Matrixdarstellung und Ergebnissen.

Abb. 3: Verteilungsvektor $\overrightarrow{v}_2$

(3)

$\blacktriangleright$ Überlebensrate der Küken berechnen

$\begin{array}[t]{rll} p_3&=& 0,5\cdot 0,7\cdot 0,79 \\[5pt] &=&\dfrac{553}{2.000} \\[5pt] &=& 0,2765 \\[5pt] &=& 27,65\,\% \end{array}$

Drei Jahre nach dem Schlüpfen leben ca. $27,65\,\%$ der Küken noch.

$\blacktriangleright$ Verteilung des Vorjahres ermitteln

$\overrightarrow{v}_t$ kannst du aus der Aufgabenstellung ablesen:

$\overrightarrow{v}_t = \begin{pmatrix}60 \\ 20 \\ 100 \end{pmatrix}$

Du erhältst folgende Gleichung:

$A \cdot \overrightarrow{v}_{t-1}= \overrightarrow{v}_t$

Vollständige Lösung anzeigen

Daraus ergibt sich folgendes Gleichungssystem:

$\begin{array}{} \text{I}\quad&60&=& \quad 0,6z\\ \text{II}\quad&20&=& \quad 0,5x\\ \text{III}\quad&100&=& \quad 0,7y+0,79z\\ \end{array}$

Aus $\text{I}$ kannst du direkt eine Lösung für $z$ bestimmen:

$\begin{array}[t]{rll} 60&=& 0,6z &\quad \scriptsize \mid\; :0,6 \\[5pt] 100&=& z \\[5pt] \end{array}$

Aus $\text{II}$ kannst du eine Lösung für $x$ bestimmen:

$\begin{array}[t]{rll} 20&=& 0,5x &\quad \scriptsize \mid\; :0,5 \\[5pt] 40&=& x \\[5pt] \end{array}$

Die Lösung für $z$ kannst du nun in $\text{III}$ einsetzen und erhältst dann eine Lösung für $y$ :

Im Jahr zuvor gab es nach der Modellierung durch die Matrix $A$ $40$ Küken, $30$ Jungvögel und $100$ Altvögel.

(1)

$\blacktriangleright$ $\boldsymbol{x}$ und $\boldsymbol{y}$ bestimmen

Du sollst $x$ und $y$ so bestimmen, dass folgende Gleichung erfüllt ist:

$A \cdot \begin{pmatrix}x\\ 9 \\ 30 \end{pmatrix} = y \cdot \begin{pmatrix}x\\9\\30 \end{pmatrix}$

Setzt du dort $A$ ein, kannst du ein Gleichungssystem aufstellen, das du nach $x$ und $y$ lösen kannst.

$\begin{pmatrix} 0,6\cdot 30 \\ 0,5x\\ 0,7\cdot 9 + 0,79\cdot 30\end{pmatrix}=\begin{pmatrix}xy\\9y\\30y\end{pmatrix}$

Vollständige Lösung anzeigen

Du erhältst folgendes Gleichungssystem:

$\begin{array}{} \text{I}\quad&18&=& xy\quad \\ \text{II}\quad&0,5x&=&9y\quad\\ \text{III}\quad&30&=&30y\quad\\ \end{array}$

Aus der dritten Gleichung erhältst du direkt:

$\begin{array}[t]{rll} 30&=& 30y&\quad \scriptsize \mid\;:30 \\[5pt] 1&=& y \end{array}$

Dies kannst du nun in $\text{I}$ einsetzen und erhältst:

$18 = x\cdot y =x\cdot 1 = x$

Zur Kontrolle kannst du nun deine Ergebnisse noch in $\text{II}$ einsetzen:

$\begin{array}[t]{rll} 0,5x&=& 9y \\[5pt] 0,5 \cdot 18&=&9\cdot 1 \\[5pt] 9&=&9\\[5pt] \end{array}$

Für $x = 18$ und $y= 1$ ist die gegebene Gleichung erfüllt.

(2)

$\blacktriangleright$ Sachverhalt interpretieren

(1)

$\blacktriangleright$ Matrizen im Sachzusammenhang vergleichen

Du sollst die Matrizen $A$ und $B$ im Sachzusammenhang vergleichen:

$A = \begin{pmatrix}0 & 0 & 0,6 \\ 0,5 & 0 & 0 \\ 0 & 0,7 & 0,79 \end{pmatrix}\quad$

$\quad B = \begin{pmatrix}0 & 0& 0,7 \\ 0,6 & 0 & 0 \\ 0 & 0,75 & 0,8 \end{pmatrix}$

Die Elemente, die schon in $A$ Null waren, sind auch in $B$ Null. Vergleiche also die von Null verschiedenen Einträge.

(2)

$\blacktriangleright$ Aussage beurteilen

$\overrightarrow{w}_0 = \begin{pmatrix}w\\w\\w\end{pmatrix}$

$\overrightarrow{w}_3 = B^3 \cdot \overrightarrow{w}_0 =\begin{pmatrix}1,183w\\ 0,651w\\ 1,667w \end{pmatrix}$

Vollständige Lösung anzeigen

Die Gesamtanzahl der Vögel der Population $w_t$ ergibt sich dann wie folgt:

$w_0 = 3w$

$w_3 = 3,501w$

Vollständige Lösung anzeigen

Es ergibt sich also:

$\dfrac{w_3}{w_0}= \dfrac{3,501w}{3w}= 1,167$

Die Gesamtanzahl der Tiere nimmt nur um $16,7\,\%$ zu, also ist die Aussage der Forschungsgruppe falsch.

(3)

$\blacktriangleright$ Überlebensrate untersuchen

$B_u \cdot \overrightarrow{s} = \overrightarrow{s}$

$\begin{pmatrix}0\cdot s_1 + 0\cdot s_2 + 0,7s_3\\0,6s_1 + 0\cdot s_2 + 0\cdot s_3\\0\cdot s_1 + 0,75s_2 + us_3 \end{pmatrix}= \begin{pmatrix}s_1 \\s_2\\s_3 \end{pmatrix}$

Vollständige Lösung anzeigen

Du erhältst also folgendes Gleichungssystem:

$\begin{array}{} \text{I}\quad&s_1&=& \quad 0,7s_3\\ \text{II}\quad&s_2&=& \quad 0,6s_1\\ \text{III}\quad&s_3&=&\quad 0,75s_2 + us_3\\ \end{array}$

Setze nun nacheinander erst $\text{I}$ in $\text{II}$ und dies dann wiederum in $\text{III}$ ein, damit $\text{III}$ nur noch von $s_3$ und $u$ abhängt:

$s_2= 0,42s_3\quad$ $(-0,685+u)s_3 = 0$

Vollständige Lösung anzeigen

$\begin{array}[t]{rll} -0,685+u&=& 0&\quad \scriptsize \mid\; +0,685 \\[5pt] u&=&0,685 \\[5pt] \end{array}$

Bei einer Überlebensrate von $u = 0,685 = 68,5\,\%$ gibt es eine von Null verschiedene Verteilung, die sich im nächsten Jahr wieder ergibt.

(4)

$\blacktriangleright$ Anzahlen bestimmen

$\begin{array}[t]{rll} s_2&=& 0,42s_3 \\[5pt] &=&0,42\cdot 50 \\[5pt] &=& 21 \\[10pt] s_1&=&0,7s_3 \\[5pt] &=& 0,7\cdot 50 \\[5pt] &=& 35 \\[5pt] \end{array}$

In der Population, die jedes Jahr gleich bleibt, gibt es neben den $50$ Altvögeln $35$ Küken und $21$ Jungvögel.

Bildnachweise [nach oben]

[1]

[2]

[3]