Aufgabe 2
Aufgabenstellung
Eine Familie will ihren Bedarf an Wärmeenergie (thermischer Energie) für Heizung und Warmwasser teilweise durch eine thermische Solaranlage (kurz: Solaranlage) decken. Anhand der Angaben des Solaranlagenherstellers und der Verbrauchswerte der Familie aus dem letzten Kalenderjahr wurde das folgende Modell für ein beispielhaftes Kalenderjahr aufgestellt.
Die Leistung der Solaranlage wird durch die Funktion mit der Gleichung
mit der Gleichung
 ,
,  ,
und der thermische Leistungsbedarf der Familie (kurz: Leistungsbedarf) durch die Funktion
,
und der thermische Leistungsbedarf der Familie (kurz: Leistungsbedarf) durch die Funktion  mit der Gleichung
mit der Gleichung
 ,
,  ,
modelliert, und zwar für das Zeitintervall
,
modelliert, und zwar für das Zeitintervall ![\([0;12]\)](https://www.schullv.de/resources/formulas/5ba9b38204a320e9433651393178f89e741e0a72de8e09a0201574090d0733c6_light.svg) , das dem Kalenderjahr entspricht.
, das dem Kalenderjahr entspricht.
Dabei fasst man als Maßzahl zur Einheit
als Maßzahl zur Einheit  Monat und
Monat und  sowie
sowie  als Maßzahlen zur Einheit
als Maßzahlen zur Einheit  Kilowattstunde pro Monat [kWh/Monat] auf. (Im Modell umfasst jeder Monat
Kilowattstunde pro Monat [kWh/Monat] auf. (Im Modell umfasst jeder Monat  Tage.) Der Zeitpunkt
Tage.) Der Zeitpunkt  entspricht dem Beginn des Kalenderjahres.
entspricht dem Beginn des Kalenderjahres.
Die Graphen von und
und  sind in der Abbildung unten dargestellt.
sind in der Abbildung unten dargestellt.
 ist im Sachzusammenhang die aus der Solaranlage im Zeitintervall
ist im Sachzusammenhang die aus der Solaranlage im Zeitintervall ![\([a; b]\)](https://www.schullv.de/resources/formulas/55d9c86ce052c8cc565dcfb2a42d040a408cd01e6029a75d99c52b506b61c5b3_light.svg) abrufbare Energie und durch das Integral
abrufbare Energie und durch das Integral  der Energiebedarf der Familie im Zeitintervall
der Energiebedarf der Familie im Zeitintervall ![\([a; b]\)](https://www.schullv.de/resources/formulas/55d9c86ce052c8cc565dcfb2a42d040a408cd01e6029a75d99c52b506b61c5b3_light.svg) für
für  in Kilowattstunden [kWh] gegeben.
in Kilowattstunden [kWh] gegeben.
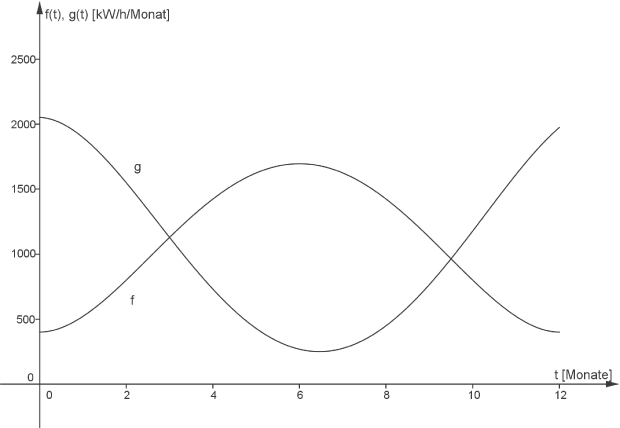 Abbildung
Abbildung
Die Leistung der Solaranlage wird durch die Funktion
Dabei fasst man
Die Graphen von
a) (1) Vergleiche die Graphen von  und
und  im Sachzusammenhang.
im Sachzusammenhang.
(5P)
(2) Berechne  und interpretiere den Wert im Sachzusammenhang.
und interpretiere den Wert im Sachzusammenhang.
(5P)
(3) Zeige, dass die Leistung der Solaranlage zu den Zeitpunkten  und
und  dem Leistungsbedarf der Familie entspricht.
dem Leistungsbedarf der Familie entspricht.
(4P)
b) (1) Bestimme den Zeitpunkt der maximalen Leistung der Solaranlage und berechne den Maximalwert.
(8P)
(2) Ermittle den Zeitpunkt im Intervall ![\([0; 12]\)](https://www.schullv.de/resources/formulas/8ed05d0a4f8f9ed6bb8571afdc6c1ea0fc69024532d36e58a766b0c636e5bb7f_light.svg) , zu dem der durch
, zu dem der durch  beschriebene Leistungsbedarf der Familie innerhalb eines Kalenderjahres am stärksten abnimmt.
beschriebene Leistungsbedarf der Familie innerhalb eines Kalenderjahres am stärksten abnimmt.
(10P)
Durch das Integral
c) (1) Gib eine Gleichung einer Stammfunktion  von
von  an und berechne den Energiebedarf der Familie für das Kalenderjahr.
an und berechne den Energiebedarf der Familie für das Kalenderjahr.
(6P)
(2) Im Intervall ![\([3; 9,5]\)](https://www.schullv.de/resources/formulas/400408585a1c81a55744509a580fa94131818436eb678403fab6c47d4d9424fc_light.svg) wird der Leistungsbedarf der Familie zu jedem Zeitpunkt durch die Solaranlage gedeckt. Die den Bedarf übersteigende Leistung der Solaranlage soll in diesem Zeitraum zusätzlich zum Heizen eines Gartenpools genutzt werden.
wird der Leistungsbedarf der Familie zu jedem Zeitpunkt durch die Solaranlage gedeckt. Die den Bedarf übersteigende Leistung der Solaranlage soll in diesem Zeitraum zusätzlich zum Heizen eines Gartenpools genutzt werden.
Ermittle die Energie, die zum Heizen des Gartenpools im Intervall![\([3; 9,5]\)](https://www.schullv.de/resources/formulas/400408585a1c81a55744509a580fa94131818436eb678403fab6c47d4d9424fc_light.svg) zur Verfügung steht.
zur Verfügung steht.
Ermittle die Energie, die zum Heizen des Gartenpools im Intervall
(6P)
(3) Skizziere in der Abbildung die Fläche, welche durch den Zähler des folgenden Bruches bestimmt wird, und interpretiere das Ergebnis der folgenden Berechnung im Sachzusammenhang.

(6P)
 Abbildung
Abbildung
a) (1)
 Vergleich von
Vergleich von  und
und  im Sachzusammenhang
Hier sollst du die Graphen von
im Sachzusammenhang
Hier sollst du die Graphen von  und
und  im Sachzusammenhang vergleichen. Die Funktion
im Sachzusammenhang vergleichen. Die Funktion  modelliert die Leistung der Solaranlage, die Funktion
modelliert die Leistung der Solaranlage, die Funktion  den Leistungsbedarf der Familie. Du erkennst, dass in den Intervallen
den Leistungsbedarf der Familie. Du erkennst, dass in den Intervallen ![\(\left[0;3\right]\)](https://www.schullv.de/resources/formulas/e6ac5d60749307c17b05c9a262850c1a1312bb0bdac1077886594150a0f01657_light.svg) und
und ![\(\left[9,5;12\right]\)](https://www.schullv.de/resources/formulas/47d231a407dc5122a8184c20a6aacccc109aaeff05e0642aed51402f3d886a66_light.svg) der Graph der Funktion
der Graph der Funktion  oberhalb des Graphen von
oberhalb des Graphen von  liegt, im Intervall
liegt, im Intervall ![\(\left[3;9,5\right]\)](https://www.schullv.de/resources/formulas/a03ac5fe1f2ee83bfa4590b6a6c79fbf40a569515ebcc534bfeed1e72a1f310a_light.svg) ist es gerade andersrum und der Graph von
ist es gerade andersrum und der Graph von  liegt über dem Graphen von
liegt über dem Graphen von  . Die Graphen von
. Die Graphen von  und
und  verhalten sich gegenläufig um einen Mittelwert von ca.
verhalten sich gegenläufig um einen Mittelwert von ca.  .
Im Sachzusammenhang lässt sich dies so deuten, dass im Winter (Intervalle
.
Im Sachzusammenhang lässt sich dies so deuten, dass im Winter (Intervalle ![\(\left[0;3\right]\)](https://www.schullv.de/resources/formulas/e6ac5d60749307c17b05c9a262850c1a1312bb0bdac1077886594150a0f01657_light.svg) und
und ![\(\left[9,5;12\right]\)](https://www.schullv.de/resources/formulas/47d231a407dc5122a8184c20a6aacccc109aaeff05e0642aed51402f3d886a66_light.svg) ) ein hoher Bedarf an Energie besteht und die Solaranlage wenig Energie generiert. Es wird somit weniger Energie generiert als verbraucht. Im Sommer (Intervall
) ein hoher Bedarf an Energie besteht und die Solaranlage wenig Energie generiert. Es wird somit weniger Energie generiert als verbraucht. Im Sommer (Intervall ![\(\left[3;9,5\right]\)](https://www.schullv.de/resources/formulas/a03ac5fe1f2ee83bfa4590b6a6c79fbf40a569515ebcc534bfeed1e72a1f310a_light.svg) ) hingegen ist die Leistung der Solaranlage groß und der Bedarf an Energie niedrig. Hier wird nun mehr Energie generiert als verbraucht.
Um den Juni (
) hingegen ist die Leistung der Solaranlage groß und der Bedarf an Energie niedrig. Hier wird nun mehr Energie generiert als verbraucht.
Um den Juni ( ) ist die Leistung der Solaranlage maximal und der Leistungsbedarf minimal. Um den Jahreswechsel (
) ist die Leistung der Solaranlage maximal und der Leistungsbedarf minimal. Um den Jahreswechsel ( bzw.
bzw.  ) ist die Leistung der Solaranlage minimal und der Leistungsbedarf maximal.
(2)
) ist die Leistung der Solaranlage minimal und der Leistungsbedarf maximal.
(2)

 berechnen und im Sachzusammenhang interpretieren
Zuerst sollst du den Wert
berechnen und im Sachzusammenhang interpretieren
Zuerst sollst du den Wert  berechnen. Um die Werte
berechnen. Um die Werte  bzw.
bzw.  zu berechnen, setze jeweils
zu berechnen, setze jeweils  in die Funktionsgleichungen von
in die Funktionsgleichungen von  bzw.
bzw.  ein:
ein:
 Nun sollst du noch diesen Wert interpretieren.
Nun sollst du noch diesen Wert interpretieren.  repräsentiert hier die Leistung der Solaranlage zum Zeitpunkt
repräsentiert hier die Leistung der Solaranlage zum Zeitpunkt  , also zu Beginn des Jahres,
, also zu Beginn des Jahres,  den Leistungsbedarf zu Beginn des Jahres. Der Quotient dieser beiden Werte ist der Anteil an Leistungsbedarf, der von der Solaranlage gedeckt wird. Es wird also zu Beginn des Jahres
den Leistungsbedarf zu Beginn des Jahres. Der Quotient dieser beiden Werte ist der Anteil an Leistungsbedarf, der von der Solaranlage gedeckt wird. Es wird also zu Beginn des Jahres  des Leistungsbedarf von der Solaranlage gedeckt.
(3)
des Leistungsbedarf von der Solaranlage gedeckt.
(3)
 Zeigen, dass Leistung der Solaranlage dem Leistungsbedarf entspricht
Hier ist nun deine Aufgabe zu zeigen, dass die Leistung der Solaranlage und der Leistungsbedarf der Familie zu den Zeitpunkten
Zeigen, dass Leistung der Solaranlage dem Leistungsbedarf entspricht
Hier ist nun deine Aufgabe zu zeigen, dass die Leistung der Solaranlage und der Leistungsbedarf der Familie zu den Zeitpunkten  und
und  gleich sind. Berechne hierzu die beiden Funktionswerte
gleich sind. Berechne hierzu die beiden Funktionswerte  und
und  bzw.
bzw.  und
und  und überprüfe diese auf Gleichheit.
und überprüfe diese auf Gleichheit.
 Zeitpunkt
Zeitpunkt  :
:
![\(\begin{array}[t]{rll}
f(3)&=3^4-24\cdot 3^3 + 144\cdot 3^2 + 400 \\[5pt]
&=81-648+1.296+400=1.129\\[5pt]
g(3)&=-3^4 +26\cdot 3^3 -167,5 \cdot 3^2 -12,5 \cdot 3 +2.053 \\[5pt]
&=-81 + 702 - 1.507,5 - 37,5 + 2.053 =1.129
\end{array}\)](https://www.schullv.de/resources/formulas/48fc1f40397a9fd099ad26b52927ca2ef68eb5d1238e3b92e042c83ccb1e9638_light.svg) Somit gilt
Somit gilt  , also sind Leistung der Solaranlage und der Leistungsbedarf gleich.
, also sind Leistung der Solaranlage und der Leistungsbedarf gleich.
 Zeitpunkt
Zeitpunkt  :
:
![\(\begin{array}[t]{rll}
f(9,5)&={9,5}^4-24\cdot {9,5}^3 + 144\cdot {9,5}^2 + 400 \\[5pt]
&=8.145,0625 - 20.577 + 12.996 + 400 = 964,0625\\[5pt]
g(9,5)&=-{9,5}^4 +26\cdot {9,5}^3 -167,5 \cdot {9,5}^2 -12,5 \cdot 9,5 +2.053 \\[5pt]
&=-8.145,0625 + 22.291,75 - 15.116,875 - 118,75 + 2.053 = 964,0625
\end{array}\)](https://www.schullv.de/resources/formulas/700bb76a49f228d68e41aaa083f677d6be09064f0cc9f33e87eda91f42fb7a0a_light.svg) Somit gilt
Somit gilt  , also sind Leistung der Solaranlage und der Leistungsbedarf gleich.
, also sind Leistung der Solaranlage und der Leistungsbedarf gleich.
b) (1)
 Maximale Leistung der Solaranlage und deren Zeitpunkt bestimmen
Deine Aufgabe ist es, den Zeitpunkt der maximalen Leistung der Solaranlage und den dazugehörigen Maximalwert zu bestimmen. Die Leistung der Solaranlage wird durch die Funktion
Maximale Leistung der Solaranlage und deren Zeitpunkt bestimmen
Deine Aufgabe ist es, den Zeitpunkt der maximalen Leistung der Solaranlage und den dazugehörigen Maximalwert zu bestimmen. Die Leistung der Solaranlage wird durch die Funktion  beschrieben, also suchst du die Maximalstelle und den Maximalwert der Funktion
beschrieben, also suchst du die Maximalstelle und den Maximalwert der Funktion  . Diese kannst du per Hand oder mit deinem GTR bestimmen.
. Diese kannst du per Hand oder mit deinem GTR bestimmen.
 Lösungsweg A: Lösen per Hand
Eine Extremstelle einer Funktion ist durch die notwendige und hinreichende Bedingung bestimmt. Die Maximalstelle und den Maximalwert kannst du folgendermaßen berechnen:
Lösungsweg A: Lösen per Hand
Eine Extremstelle einer Funktion ist durch die notwendige und hinreichende Bedingung bestimmt. Die Maximalstelle und den Maximalwert kannst du folgendermaßen berechnen:
 bestimmen
bestimmen
![\(\begin{array}[t]{rll}
f(t)&=t^4-24 \cdot t^3 + 144 \cdot t^2 +400\\[10pt]
f‘(t)&=4\cdot t^3 - 24 \cdot \left(3 \cdot t^2\right) + 144 \cdot \left(2 \cdot t\right) \\[5pt]
&=4\cdot t^3 - 72\cdot t^2 + 288 \cdot t \\[10pt]
f‘‘(t)&=4\cdot \left(3\cdot t^2\right) - 72\cdot \left(2\cdot t\right) + 288 \\[5pt]
&=12 \cdot t^2 - 144 \cdot t +288
\end{array}\)](https://www.schullv.de/resources/formulas/ddff306844f10a6a5675de3a6c568c42bf729d1374e98c8bab4db0599d5a7b41_light.svg) 2. Schritt: Notwendiges Kriterium anwenden
Setze hier die erste Ableitungsfunktion von
2. Schritt: Notwendiges Kriterium anwenden
Setze hier die erste Ableitungsfunktion von  gleich Null und ermittle die Nullstellen:
gleich Null und ermittle die Nullstellen:
![\(\begin{array}[t]{rll}
0\stackrel{!}{=}&f‘(t) \\[5pt]
0=&4\cdot t^3 - 72\cdot t^2 + 288 \cdot t \\[5pt]
0=&t \cdot \left(4\cdot t^2 - 72\cdot t + 288 \right)
\end{array}\)](https://www.schullv.de/resources/formulas/0a65a939a0f3521e922f304ed500f03c0c644c0d825b4ebb5b9d44c96118a75e_light.svg) Nach dem Satz über das Nullprodukt kann ein Produkt nur Null sein, falls einer der Faktoren gleich Null ist. Somit sind hier die Möglichkeiten, dass
Nach dem Satz über das Nullprodukt kann ein Produkt nur Null sein, falls einer der Faktoren gleich Null ist. Somit sind hier die Möglichkeiten, dass  ist oder
ist oder  ist. Somit ist
ist. Somit ist  die erste mögliche Nullstelle. Betrachte nun den Term
die erste mögliche Nullstelle. Betrachte nun den Term  und ermittle die
und ermittle die  , für die er gleich Null ist. Dies kannst du entweder mit der Mitternachtsformel oder mit der PQ-Formel.
, für die er gleich Null ist. Dies kannst du entweder mit der Mitternachtsformel oder mit der PQ-Formel.
 Lösungsweg A1: PQ-Formel
Bringe dazu den Term auf die passende Form:
Lösungsweg A1: PQ-Formel
Bringe dazu den Term auf die passende Form:
![\(\begin{array}{rll}
0=&4\cdot t^2 - 72\cdot t + 288&\quad\mid\; :4 \\[5pt]
0=&t^2-18t+72
\end{array}\)](https://www.schullv.de/resources/formulas/1fd2c4300a6e6dbaa2a267eed18fa01e5bb95a38d98386ba26f577470936ad20_light.svg) Hier ist nun
Hier ist nun  und
und  :
:
![\(\begin{array}{rll}
t_{2,3} =& - \dfrac{-18}{2} \pm \sqrt{\left( {\frac{-18}{2}} \right)^2 - 72} \\[5pt]
t_{2,3} =& 9 \pm \sqrt {81 - 72}\\[5pt]
t_{2,3} =& 9 \pm \sqrt {9}\\[5pt]
t_{2,3} =& 9 \pm 3
\end{array}\)](https://www.schullv.de/resources/formulas/b5422c04a6072513b89517635122aba0637b136260857c4be860499b3f0343a1_light.svg) Die Extremstellen der Funktion
Die Extremstellen der Funktion  sind somit
sind somit  ,
,  und
und  .
.
 Lösungsweg A2: Mitternachtsformel
Du kannst die Mitternachtsformel hier direkt anwenden, wobei
Lösungsweg A2: Mitternachtsformel
Du kannst die Mitternachtsformel hier direkt anwenden, wobei  ,
,  und
und  :
:
![\(\begin{array}[t]{rll}
t_{2,3} =& \dfrac{{ - (-72) \pm \sqrt {(-72)^2 - 4 \cdot 4 \cdot 288} }}{{2\cdot 4}}\\[5pt]
t_{2,3} =&\dfrac{{ 72 \pm \sqrt {5.184 - 4.608} }}{{8}}\\[5pt]
t_{2,3} =&9 \pm \dfrac{\sqrt{576}}{8} \\[5pt]
t_{2,3} =&9 \pm \dfrac{24}{8} \\[5pt]
t_{2,3} =& 9 \pm 3
\end{array}\)](https://www.schullv.de/resources/formulas/4b4f4c6fa5edf278dca95a3cd418ee4633828361cbef2c1c1e048ad813e0ea5b_light.svg) Die Extremstellen der Funktion
Die Extremstellen der Funktion  sind somit
sind somit  ,
,  und
und  .
3. Schritt: Hinreichendes Kriterium überprüfen
Setze nun
.
3. Schritt: Hinreichendes Kriterium überprüfen
Setze nun  ,
,  und
und  in
in  ein:
ein:
 Zeitpunkt
Zeitpunkt  :
:
 , also ist
, also ist  Tiefstelle der Funktion
Tiefstelle der Funktion  .
.
 Zeitpunkt
Zeitpunkt  :
:
 , also ist
, also ist  Tiefstelle der Funktion
Tiefstelle der Funktion  .
.
 Zeitpunkt
Zeitpunkt  :
:
 , also ist
, also ist  die gesuchte Maximalstelle der Funktion
die gesuchte Maximalstelle der Funktion  .
4. Schritt: Maximalwert berechnen
Nun musst du noch den Maximalwert an der Stelle
.
4. Schritt: Maximalwert berechnen
Nun musst du noch den Maximalwert an der Stelle  berechnen. Setze dazu
berechnen. Setze dazu  in die Funktionsgleichung
in die Funktionsgleichung  ein:
ein:
![\(\begin{array}[t]{rll}
f(6)&=6^4-24 \cdot 6^3 +144 \cdot 6^2 +400 \\[5pt]
&=1.296 -5.184 + 5.184 +400= 1.696
\end{array}\)](https://www.schullv.de/resources/formulas/cba32a0c2c7e5e48b31e2ece09c772b4382bec77de09a3e79edf7a9312b78da0_light.svg) Damit ist die Leistung der Solaranlage zum Zeitpunkt
Damit ist die Leistung der Solaranlage zum Zeitpunkt  maximal und hat einen Maximalwert von
maximal und hat einen Maximalwert von  .
.
 Lösungsweg B: Lösen mit dem GTR
Wechsle mit deinem GTR in das GRAPH-Menü und speichere dort den Funktionsterm von
Lösungsweg B: Lösen mit dem GTR
Wechsle mit deinem GTR in das GRAPH-Menü und speichere dort den Funktionsterm von  . Hast du diesen dort eingegeben, dann passe das Fenster so an, dass du den gewünschten Bereich sehen kannst.
Wähle dann unter
. Hast du diesen dort eingegeben, dann passe das Fenster so an, dass du den gewünschten Bereich sehen kannst.
Wähle dann unter
 und
und  ein.
ein.
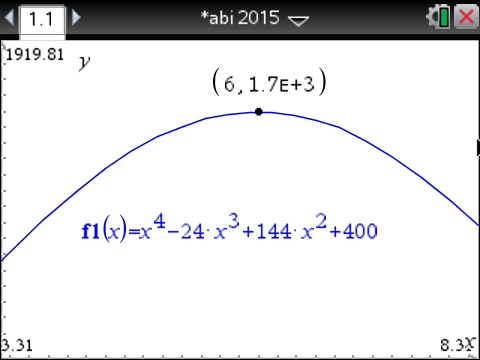 Damit ist die Leistung der Solaranlage zum Zeitpunkt
Damit ist die Leistung der Solaranlage zum Zeitpunkt  maximal und hat einen Maximalwert von
maximal und hat einen Maximalwert von  .
(2)
.
(2)
 Zeitpunkt der maximalen Abnahme des Leistungsbedarfs bestimmen
Gesucht ist der Zeitpunkt im Intervall
Zeitpunkt der maximalen Abnahme des Leistungsbedarfs bestimmen
Gesucht ist der Zeitpunkt im Intervall ![\([0;12]\)](https://www.schullv.de/resources/formulas/5ba9b38204a320e9433651393178f89e741e0a72de8e09a0201574090d0733c6_light.svg) , zu dem der durch
, zu dem der durch  beschriebene Leistungsbedarf am stärksten abnimmt. Dies kannst du auch folgendermaßen interpretieren:
Die Änderungsrate
beschriebene Leistungsbedarf am stärksten abnimmt. Dies kannst du auch folgendermaßen interpretieren:
Die Änderungsrate  beschreibt die Zu- oder Abnahme des Leistungsbedarf der Familie. Da der Zeitpunkt der stärksten Abnahme gesucht ist, erhältst du diesen durch das Bestimmen des Minimums der Änderungsrate
beschreibt die Zu- oder Abnahme des Leistungsbedarf der Familie. Da der Zeitpunkt der stärksten Abnahme gesucht ist, erhältst du diesen durch das Bestimmen des Minimums der Änderungsrate  . Leite also
. Leite also  ab und bestimme anschließend die Minimalstelle der Ableitung. Dieses kannst du per Hand oder mit deinem GTR bestimmen.
ab und bestimme anschließend die Minimalstelle der Ableitung. Dieses kannst du per Hand oder mit deinem GTR bestimmen.
 Lösungsweg A: Lösen per Hand
Eine Extremstelle einer Funktion ist durch die notwendige und hinreichende Bedingung bestimmt. Die Minimalstelle von
Lösungsweg A: Lösen per Hand
Eine Extremstelle einer Funktion ist durch die notwendige und hinreichende Bedingung bestimmt. Die Minimalstelle von  kannst du folgendermaßen berechnen:
kannst du folgendermaßen berechnen:
 bilden
bilden
![\(\begin{array}[t]{rll}
g(t)&=-t^4 + 26 \cdot t^3 - 167,5 \cdot t^2 -12,5 \cdot t + 2.053\\[10pt]
g‘(t)&=-\left(4\cdot t^3\right) + 26 \cdot \left(3 \cdot t^2\right) -167,5 \cdot \left(2 \cdot t\right) - 12,5\\[5pt]
&=-4\cdot t^3 + 78\cdot t^2 -335 \cdot t -12,5 \\[10pt]
g‘‘(t)&=-4\cdot \left(3\cdot t^2\right) + 78 \cdot \left(2\cdot t\right) - 335 \\[5pt]
&=-12 \cdot t^2 + 156 \cdot t -335 \\[10pt]
g‘‘‘(t)&=-12\cdot \left(2\cdot t\right) + 156 \\[5pt]
&=-24 \cdot t + 156
\end{array}\)](https://www.schullv.de/resources/formulas/97e55d68dc1e887ab038ee8b8abfe571d311ee01fedf0d6936b061be7c1d55de_light.svg) 2. Schritt: Notwendiges Kriteriumn anwenden
Setze hier die erste Ableitungsfunktion von
2. Schritt: Notwendiges Kriteriumn anwenden
Setze hier die erste Ableitungsfunktion von  , also
, also  , gleich Null und ermittle die Nullstellen:
, gleich Null und ermittle die Nullstellen:
![\(\begin{array}[t]{rll}
0\stackrel{!}{=}&g‘‘(t) \\[5pt]
0=&-12 \cdot t^2 + 156 \cdot t -335
\end{array}\)](https://www.schullv.de/resources/formulas/42f74cfec63f01683192ba9c98c59a9d8797a2af428efa08e821b2d59156608a_light.svg) Hier kannst du entweder die PQ-Formel oder die Mitternachtsformel verwenden, um die Nullstellen zu bestimmen.
Hier kannst du entweder die PQ-Formel oder die Mitternachtsformel verwenden, um die Nullstellen zu bestimmen.
 Lösungsweg A1: PQ-Formel
Bringe dazu den Term auf die passende Form:
Lösungsweg A1: PQ-Formel
Bringe dazu den Term auf die passende Form:
![\(\begin{array}{rll}
0=&-12 \cdot t^2 + 156 \cdot t -335 &\quad\mid\; :\left(-12\right) \\[5pt]
0=&t^2-13t+\dfrac{335}{12}
\end{array}\)](https://www.schullv.de/resources/formulas/52d4f38dfd7712e719ca1f64a493af096a971edbaecc3c38b39543fb8a1a909f_light.svg) Hier ist nun
Hier ist nun  und
und  :
:
![\(\begin{array}{rll}
t_{1,2} =& - \dfrac{-13}{2} \pm \sqrt{\left( {\frac{-13}{2}} \right)^2 - \frac{335}{12}} \\[5pt]
t_{1,2} =& \dfrac{13}{2} \pm \sqrt {\frac{169}{4} - \frac{335}{12}}\\[5pt]
t_{1,2} =& \dfrac{13}{2} \pm \sqrt {\frac{43}{3}}\\[5pt]
t_{1,2} =& 6,5 \pm 3,79
\end{array}\)](https://www.schullv.de/resources/formulas/dd1ec7a1318e2642ba8d0aebd164341b7385be0e0cb5dd3f13cb0615d3b05620_light.svg) Die Minimalstellen der ersten Ableitung
Die Minimalstellen der ersten Ableitung  sind somit
sind somit  und
und  .
.
 Lösungsweg A2: Mitternachtsformel
Du kannst die Mitternachtsformel hier direkt anwenden, wobei
Lösungsweg A2: Mitternachtsformel
Du kannst die Mitternachtsformel hier direkt anwenden, wobei  ,
,  und
und  :
:
![\(\begin{array}[t]{rll}
t_{1,2} =& \dfrac{{ - 156 \pm \sqrt {156^2 - 4 \cdot (-12) \cdot (-335)} }}{{2\cdot (-12)}}\\[5pt]
t_{1,2} =&\dfrac{{ 156 \pm \sqrt {24.336 - 16.080} }}{{24}}\\[5pt]
t_{1,2} =& \dfrac{13}{2} \pm \dfrac{\sqrt{8.256}}{24} \\[5pt]
t_{1,2} =& 6,5 \pm 3,79
\end{array}\)](https://www.schullv.de/resources/formulas/f39c725e9489b337082019b891b76f3e798c18d95bd4ed4a2e70ae75fffe68d0_light.svg) Die Minimalstellen der ersten Ableitung
Die Minimalstellen der ersten Ableitung  sind somit
sind somit  und
und  .
3. Schritt: Hinreichende Bedingung überprüfen
Setze nun
.
3. Schritt: Hinreichende Bedingung überprüfen
Setze nun  und
und  in
in  ein:
ein:
 Zeitpunkt
Zeitpunkt  :
:
 , also ist
, also ist  Maximalstelle der ersten Ableitung
Maximalstelle der ersten Ableitung  .
.
 Zeitpunkt
Zeitpunkt  :
:
 , also ist
, also ist  Minimalstelle der ersten Ableitung
Minimalstelle der ersten Ableitung  .
4. Schritt: Überprüfen der Randwerte
Berechne hier die Randwerte der ersten Ableitung
.
4. Schritt: Überprüfen der Randwerte
Berechne hier die Randwerte der ersten Ableitung  im Intervall
im Intervall ![\(\left[0;12\right]\)](https://www.schullv.de/resources/formulas/e2619fcaf7c9c53ab88bd0639e6ab76dffa4b2db3d6bb88b44a0b3e6c4238547_light.svg) und vergleiche diese mit dem Minimalwert. Setze dazu
und vergleiche diese mit dem Minimalwert. Setze dazu  ,
,  und
und  in
in  ein:
ein:
 Zeitpunkt
Zeitpunkt  :
:
 ist der Minimalwert der oben berechneten Minimalstelle der ersten Ableitung
ist der Minimalwert der oben berechneten Minimalstelle der ersten Ableitung  .
.
 Zeitpunkt
Zeitpunkt  :
:
 , also ist der Randwert
, also ist der Randwert  nicht Zeitpunkt maximaler Abnahme.
nicht Zeitpunkt maximaler Abnahme.
 Zeitpunkt
Zeitpunkt  :
:
 , also ist der Randwert
, also ist der Randwert  nicht Zeitpunkt maximaler Abnahme.
Der Leistungsbedarf nimmt somit zum Zeitpunkt
nicht Zeitpunkt maximaler Abnahme.
Der Leistungsbedarf nimmt somit zum Zeitpunkt  am stärksten ab.
am stärksten ab.
 Lösungsweg B: Lösen mit dem GTR
Berechne wie im Lösungsweg A die erste Ableitung
Lösungsweg B: Lösen mit dem GTR
Berechne wie im Lösungsweg A die erste Ableitung  . Wechsle anschließend mit deinem GTR in das GRAPH-Menü und speichere dort den Funktionsterm von
. Wechsle anschließend mit deinem GTR in das GRAPH-Menü und speichere dort den Funktionsterm von  . Hast du diesen dort eingegeben, dann wähle das Fenster so, dass du den gewünschten Bereich sehen kannst.
Wähle dann unter
. Hast du diesen dort eingegeben, dann wähle das Fenster so, dass du den gewünschten Bereich sehen kannst.
Wähle dann unter
 und
und  ein.
ein.
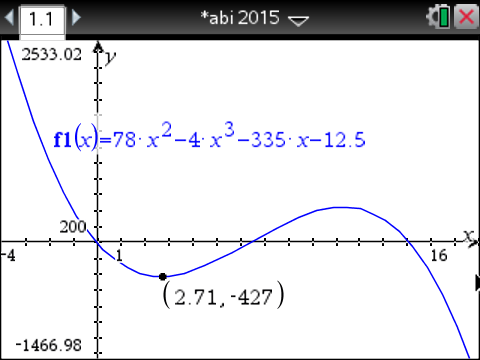 Also besitzt die Funktion
Also besitzt die Funktion  an der Stelle
an der Stelle  ein Minimum. Somit ist
ein Minimum. Somit ist  der Zeitpunkt im Intervall
der Zeitpunkt im Intervall ![\([0;12]\)](https://www.schullv.de/resources/formulas/5ba9b38204a320e9433651393178f89e741e0a72de8e09a0201574090d0733c6_light.svg) , an dem der Leistungsbedarf der Familie innerhalb dieses Kalenderjahres am stärksten abnimmt.
, an dem der Leistungsbedarf der Familie innerhalb dieses Kalenderjahres am stärksten abnimmt.
- Bestimme die erste und zweite Ableitung von
.
- Wende das notwendige Kriterium an. Für eine potenzielle Extremstelle
gilt:
Setze also
und löse nach
auf, um die möglichen Extremstellen zu bestimmen.
- Hinreichendes Kriterium überprüfen. Ist
für eine potenzielle Extremstelle
, so handelt es sich bei
um eine Maximalstelle. Setze die potenziellen Extremstellen in die zweite Ableitung ein und überprüfe das Ergebnis auf sein Vorzeichen.
- Den Maximalwert kannst du nun bestimmen, indem du die Maximalstelle in die Funktionsgleichung von
einsetzt.
6: Graph analysieren  3: Maximum
3: Maximum
den Befehl zum Bestimmen des Maximums aus und bestätige mit Enter. Gib anschließend deine Intervallgrenzen 
- Bestimme die erste, zweite und dritte Ableitung von
.
- Wende das notwendige Kriterium an. Für eine potenzielle Extremstelle
der Funktion
gilt:
Setze also
und löse nach
auf, um die möglichen Extremstellen zu bestimmen.
- Hinreichendes Kriterium überprüfen. Ist
für eine potenzielle Extremstelle
, so handelt es sich bei
um eine Minimalstelle. Setze die potenziellen Extremstellen in die dritte Ableitung ein und überprüfe das Ergebnis auf sein Vorzeichen.
- Überprüfe nun noch die Randwerte.
Berechne dazu die Funktionswerte
und
und vergleiche sie mit dem vorher berechneten Minimawert.
6: Graph analysieren  2: Minimum
2: Minimum
den Befehl zum Bestimmen des Minimums aus und bestätige mit Enter. Gib anschließend deine Intervallgrenzen 
c) (1)
 Stammfunktion
Stammfunktion  von
von  bestimmen
Hier ist es deine Aufgabe eine Stammfunktion
bestimmen
Hier ist es deine Aufgabe eine Stammfunktion  von
von  zu bestimmen. Integriere dazu die Funktion
zu bestimmen. Integriere dazu die Funktion  :
:
![\(\begin{array}[t]{rll}
\displaystyle\int_{}^{}g(t)\;\mathrm dt&=\displaystyle\int_{}^{}-t^4+26t^3-167,5t^2-12,5t+2.053\;\mathrm dt \\[5pt]
&=-\dfrac{1}{5}t^5+\dfrac{1}{4}\cdot 26t^4- \dfrac{1}{3}\cdot 167,5t^3-\dfrac{1}{2}\cdot12,5t^2+2.053 t +c\\[5pt]
&=-\dfrac{1}{5}t^5+\dfrac{13}{2}t^4- \dfrac{335}{6}t^3-\dfrac{25}{4}t^2+2.053 t +c
\end{array}\)](https://www.schullv.de/resources/formulas/bcfbe452516fa24ea3d9ac5d54d1fe33a7b26ae59e360b7482fbd1e34b9b3966_light.svg) Für
Für  ist
ist  eine Stammfunktion von
eine Stammfunktion von  .
.
 Berechnen des Energiebedarfs der Familie
Nach Aufgabenstellung ist durch das Integral
Berechnen des Energiebedarfs der Familie
Nach Aufgabenstellung ist durch das Integral  der Energiebedarf der Familie im Zeitintervall
der Energiebedarf der Familie im Zeitintervall ![\([a;b]\)](https://www.schullv.de/resources/formulas/e84e12d6ffce2d83a82ceef8cfb5eb14688a4f4cce00a0d08d5357e2c6858142_light.svg) gegeben. Das Zeitintervall
gegeben. Das Zeitintervall ![\([0;12]\)](https://www.schullv.de/resources/formulas/5ba9b38204a320e9433651393178f89e741e0a72de8e09a0201574090d0733c6_light.svg) beschreibt hier das Kalenderjahr. Somit musst du das Integral
beschreibt hier das Kalenderjahr. Somit musst du das Integral  berechnen. Dieses kannst du per Hand oder mit deinem GTR berechnen.
berechnen. Dieses kannst du per Hand oder mit deinem GTR berechnen.
 Lösungsweg A: Per Hand
Benutze hierzu den Hauptsatz der Integralrechnung und die zuvor berechnete Stammfunktion
Lösungsweg A: Per Hand
Benutze hierzu den Hauptsatz der Integralrechnung und die zuvor berechnete Stammfunktion  :
:
![\(\begin{array}[t]{rll}
\displaystyle\int_{0}^{12}g(t)\;\mathrm dt&=G(12)-G(0)\\[5pt]
&= \left(-\dfrac{1}{5}\cdot 12^5+\dfrac{13}{2}\cdot 12^4- \dfrac{335}{6}\cdot 12^3-\dfrac{25}{4}\cdot 12^2+2.053\cdot 12\right) - 0 \\[5pt]
&=-49.766,4 + 134.784 - 96.480 - 900 + 24.636 \\[5pt]
&=12.273,6
\end{array}\)](https://www.schullv.de/resources/formulas/5e88fdf679802e4bd1935ae3bce53399fb03063d48520859bb05f563a571d9db_light.svg) Der Energiebedarf der Familie für das Kalenderjahr beträgt 12.273,6 kWh.
Der Energiebedarf der Familie für das Kalenderjahr beträgt 12.273,6 kWh.
 Lösungsweg B: Lösen mit dem GTR
Wechsle mit deinem GTR in das GRAPH-Menü und speichere dort den Funktionsterm von
Lösungsweg B: Lösen mit dem GTR
Wechsle mit deinem GTR in das GRAPH-Menü und speichere dort den Funktionsterm von  . Hast du diesen dort eingeben, dann wähle das Fenster so, dass du den gewünschten Bereich sehen kannst.
Bestimme dann über
. Hast du diesen dort eingeben, dann wähle das Fenster so, dass du den gewünschten Bereich sehen kannst.
Bestimme dann über
 in den Grenzen des Intervalls
in den Grenzen des Intervalls ![\(\left[0;12\right]\)](https://www.schullv.de/resources/formulas/e2619fcaf7c9c53ab88bd0639e6ab76dffa4b2db3d6bb88b44a0b3e6c4238547_light.svg) .
.
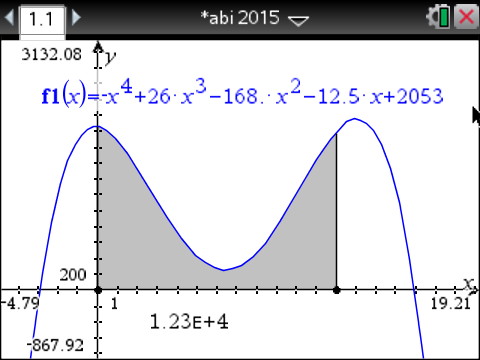 Der Energiebedarf der Familie für das Kalenderjahr beträgt 12.300 kWh.
(2)
Der Energiebedarf der Familie für das Kalenderjahr beträgt 12.300 kWh.
(2)
 Berechnen der Energie, die zum Heizen des Pools zur Verfügung steht
Der Pool wird mit der Energie geheizt, welche den Bedarf der Familie übersteigt. Dieser Leistungsüberschuss ist gerade die Differenz zwischen der von der Solaranlage erzeugten Leistung und dem Leistungsbedarf der Familie. Zum Zeitpunkt
Berechnen der Energie, die zum Heizen des Pools zur Verfügung steht
Der Pool wird mit der Energie geheizt, welche den Bedarf der Familie übersteigt. Dieser Leistungsüberschuss ist gerade die Differenz zwischen der von der Solaranlage erzeugten Leistung und dem Leistungsbedarf der Familie. Zum Zeitpunkt  ist der Leistungsüberschuss somit durch
ist der Leistungsüberschuss somit durch  gegeben.
Die überschüssige Energie im Intervall
gegeben.
Die überschüssige Energie im Intervall ![\(\left[3;9,5\right]\)](https://www.schullv.de/resources/formulas/a03ac5fe1f2ee83bfa4590b6a6c79fbf40a569515ebcc534bfeed1e72a1f310a_light.svg) kannst du durch das Integral über den Leistungsüberschuss auf dem Intervall
kannst du durch das Integral über den Leistungsüberschuss auf dem Intervall ![\(\left[3;9,5\right]\)](https://www.schullv.de/resources/formulas/a03ac5fe1f2ee83bfa4590b6a6c79fbf40a569515ebcc534bfeed1e72a1f310a_light.svg) berechnen. Gesucht ist somit das Integral:
$
berechnen. Gesucht ist somit das Integral:
$ $
Berechne also zuerst
$
Berechne also zuerst  . Danach kannst du das Integral per Hand oder mit deinem GTR bestimmen.
1. Schritt:
. Danach kannst du das Integral per Hand oder mit deinem GTR bestimmen.
1. Schritt:  berechnen
berechnen
![\(\begin{array}[t]{rll}
f(t)-g(t)&= \left(t^4-24 \cdot t^3 + 144 \cdot t^2 +400\right)-\left(-t^4 + 26 \cdot t^3 - 167,5 \cdot t^2 -12,5 \cdot t + 2.053\right) \\[5pt]
&=2\cdot t^4 - 50 \cdot t^3 + 311,5 \cdot t^2 +12,5 \cdot t -1.653
\end{array}\)](https://www.schullv.de/resources/formulas/d2483ef86d2852a157eb92c6a4e760587ca543b99a93ac46fe665e60f5fc78c4_light.svg)
 Lösungsweg A: Per Hand
Bestimme nun eine Stammfunktion
Lösungsweg A: Per Hand
Bestimme nun eine Stammfunktion  und berechne damit das Integral
und berechne damit das Integral  .
2. Schritt: Stammfunktion
.
2. Schritt: Stammfunktion  bestimmen
bestimmen
![\(\begin{array}[t]{rll}
\displaystyle\int_{}^{} \left(f(t)-g(t)\right) \;\mathrm dt&=\displaystyle\int_{}^{}2\cdot t^4 - 50 \cdot t^3 + 311,5 \cdot t^2 +12,5 \cdot t -1.653 \;\mathrm dt\\[5pt]
&=\dfrac{1}{5}\cdot 2t^5-\dfrac{1}{4}\cdot 50t^4+ \dfrac{1}{3}\cdot 311,5t^3+\dfrac{1}{2}\cdot12,5t^2-1.653 t +c\\[5pt]
&=\dfrac{2}{5}t^5-\dfrac{25}{2}t^4+ \dfrac{623}{6}t^3 +\dfrac{25}{4}t^2-1.653 t +c
\end{array}\)](https://www.schullv.de/resources/formulas/2ca820772fc352cb9528f2e91c366e1dc15c04ea40f4676f918026308640ec63_light.svg) Wähle
Wähle  und damit ist
und damit ist  eine Stammfunktion von
eine Stammfunktion von  .
3. Schritt: Integral
.
3. Schritt: Integral  berechnen
berechnen
![\(\begin{array}[t]{rll}
\displaystyle\int_{3}^{9,5} \left(f(t)-g(t)\right) \;\mathrm dt&= (F-G)(9,5)-(F-G)(3)\\[5pt]
&=\left(\dfrac{2}{5}\cdot 9,5^5-\dfrac{25}{2}\cdot 9,5^4+ \dfrac{623}{6}\cdot 9,5^3+\dfrac{25}{4}\cdot 9,5^2-1.653 \cdot 9,5\right) \\[5pt]
&- \left(\dfrac{2}{5}\cdot 3^5-\dfrac{25}{2}\cdot 3^4+ \dfrac{623}{6}\cdot 3^3+\dfrac{25}{4}\cdot 3^2-1.653 \cdot 3\right)\\[5pt]
&= 3.022,62 - \left(-3014,55\right)\\[5pt]
&= 3.022,62 + 3014,55\\[5pt]
&= 6.037,17
\end{array}\)](https://www.schullv.de/resources/formulas/0c034dfdb0375b8556fd466c25adb545f141b2477c3fb22a5b431bf1e45bb1ab_light.svg) Der Familie stehen somit
Der Familie stehen somit  kWh Energie zum Heizen des Pools zur Verfügung.
kWh Energie zum Heizen des Pools zur Verfügung.
 Lösungsweg B: Lösen mit dem GTR
Wechsle mit deinem GTR in das GRAPH-Menü und speichere dort den Funktionsterm von
Lösungsweg B: Lösen mit dem GTR
Wechsle mit deinem GTR in das GRAPH-Menü und speichere dort den Funktionsterm von  . Hast du diesen dort eingegeben, dann wähle das Fenster so, dass du den gewünschten Bereich sehen kannst.
Bestimme dann über
. Hast du diesen dort eingegeben, dann wähle das Fenster so, dass du den gewünschten Bereich sehen kannst.
Bestimme dann über
 in den Grenzen des Intervalls
in den Grenzen des Intervalls ![\(\left[3;9,5\right]\)](https://www.schullv.de/resources/formulas/a03ac5fe1f2ee83bfa4590b6a6c79fbf40a569515ebcc534bfeed1e72a1f310a_light.svg) .
.
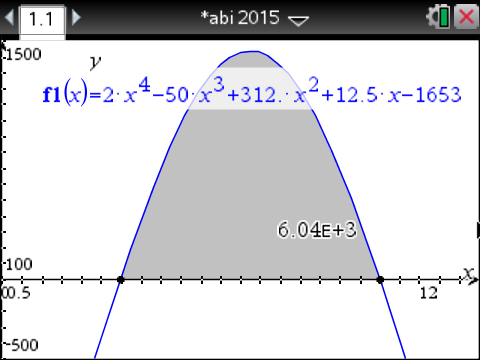 Der Familie stehen somit
Der Familie stehen somit  kWh Energie zum Heizen des Pools zur Verfügung.
(3)
kWh Energie zum Heizen des Pools zur Verfügung.
(3)
 Fläche skizzieren
Deine Aufgabe ist es, die Fläche zu skizzieren, welche durch den Zähler des Bruches bestimmt wird. Der Zähler lautet:
Fläche skizzieren
Deine Aufgabe ist es, die Fläche zu skizzieren, welche durch den Zähler des Bruches bestimmt wird. Der Zähler lautet:
 Betrachte zuerst die einzelnen Terme des Zählers:
Betrachte zuerst die einzelnen Terme des Zählers:
![\([0;3]\)](https://www.schullv.de/resources/formulas/989ef35ddb608f4befc7b703f6465b5cf517e676c006489beb40101fdaaecf76_light.svg) und
und ![\([9,5;12]\)](https://www.schullv.de/resources/formulas/49df986b392bead3550143bb8b9dc9d0d0552400a195b44330c841b4a9be9e4b_light.svg) bleibt die erste Fläche unverändert. Im Intervall
bleibt die erste Fläche unverändert. Im Intervall ![\([3;9,5]\)](https://www.schullv.de/resources/formulas/595081264c02f7af17ad1e595d0a2048c633145a0eebe49dc0c880beccea2075_light.svg) wird von der Fläche unter dem Graphen von
wird von der Fläche unter dem Graphen von  die Fläche zwischen den Graphen von
die Fläche zwischen den Graphen von  und
und  abgezogen. Du erhältst die Fläche unter dem Graphen von
abgezogen. Du erhältst die Fläche unter dem Graphen von  . Insgesamt ergibt sich die unten eingezeichnete Fläche:
. Insgesamt ergibt sich die unten eingezeichnete Fläche:
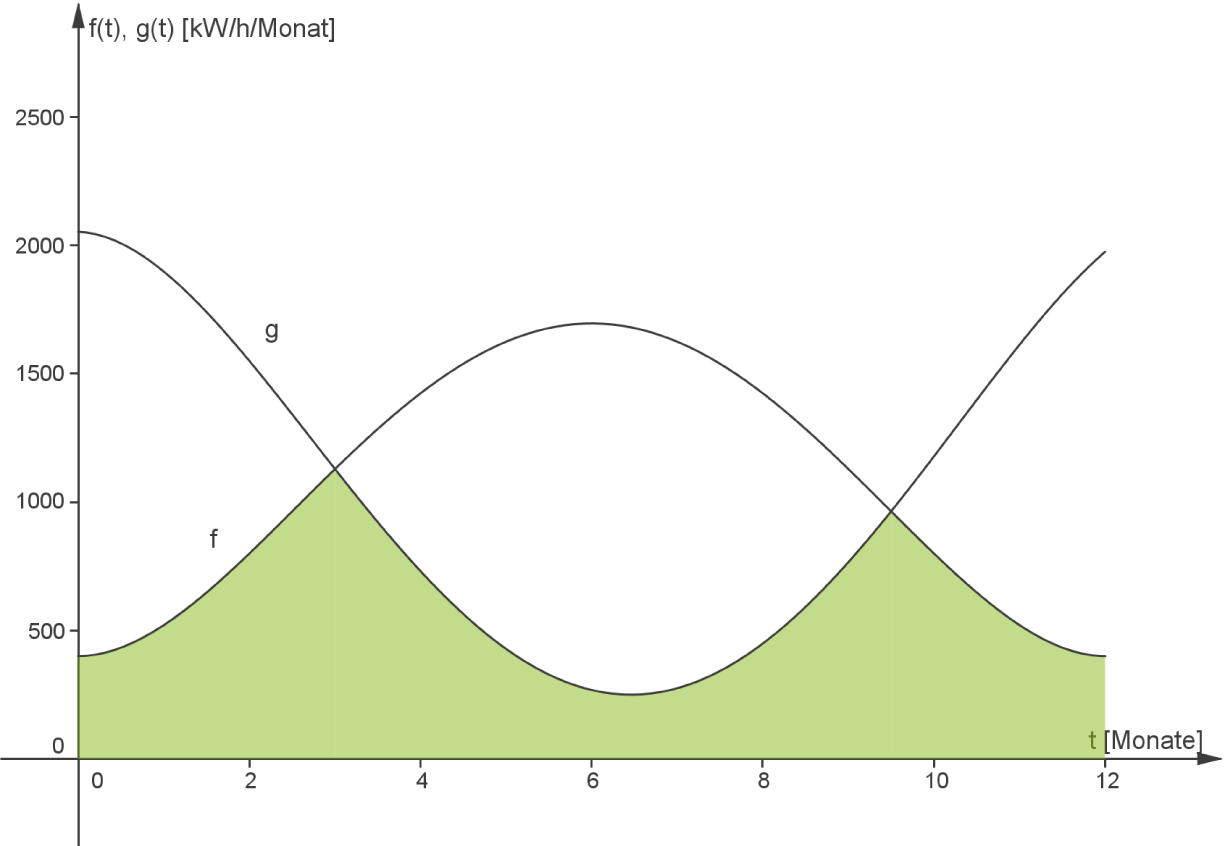
 Interpretation der Berechnung im Sachzusammenhang
Mache dir hier zuerst klar, was die drei Integrale beschreiben. Dabei helfen dir der Aufgabentext und die Aufgabe c)(2).
Interpretation der Berechnung im Sachzusammenhang
Mache dir hier zuerst klar, was die drei Integrale beschreiben. Dabei helfen dir der Aufgabentext und die Aufgabe c)(2).
 Dies bedeutet, dass die Solaranlage über das ganze Jahr ca.
Dies bedeutet, dass die Solaranlage über das ganze Jahr ca.  des Gesamtbedarfs der Familie deckt.
des Gesamtbedarfs der Familie deckt.
6: Graph analysieren  6: Integral
6: Integral  Untere Schranke 0
Untere Schranke 0  Obere Schranke 12
Obere Schranke 12
das Integral über 
6: Graph analysieren  6: Integral
6: Integral  Untere Schranke 3
Untere Schranke 3  Obere Schranke 9.5
Obere Schranke 9.5
das Integral über 
- Das erste Integral
entspricht dem Inhalt der Fläche zwischen dem Graphen der Funktion
und der
-Achse im Intervall
:
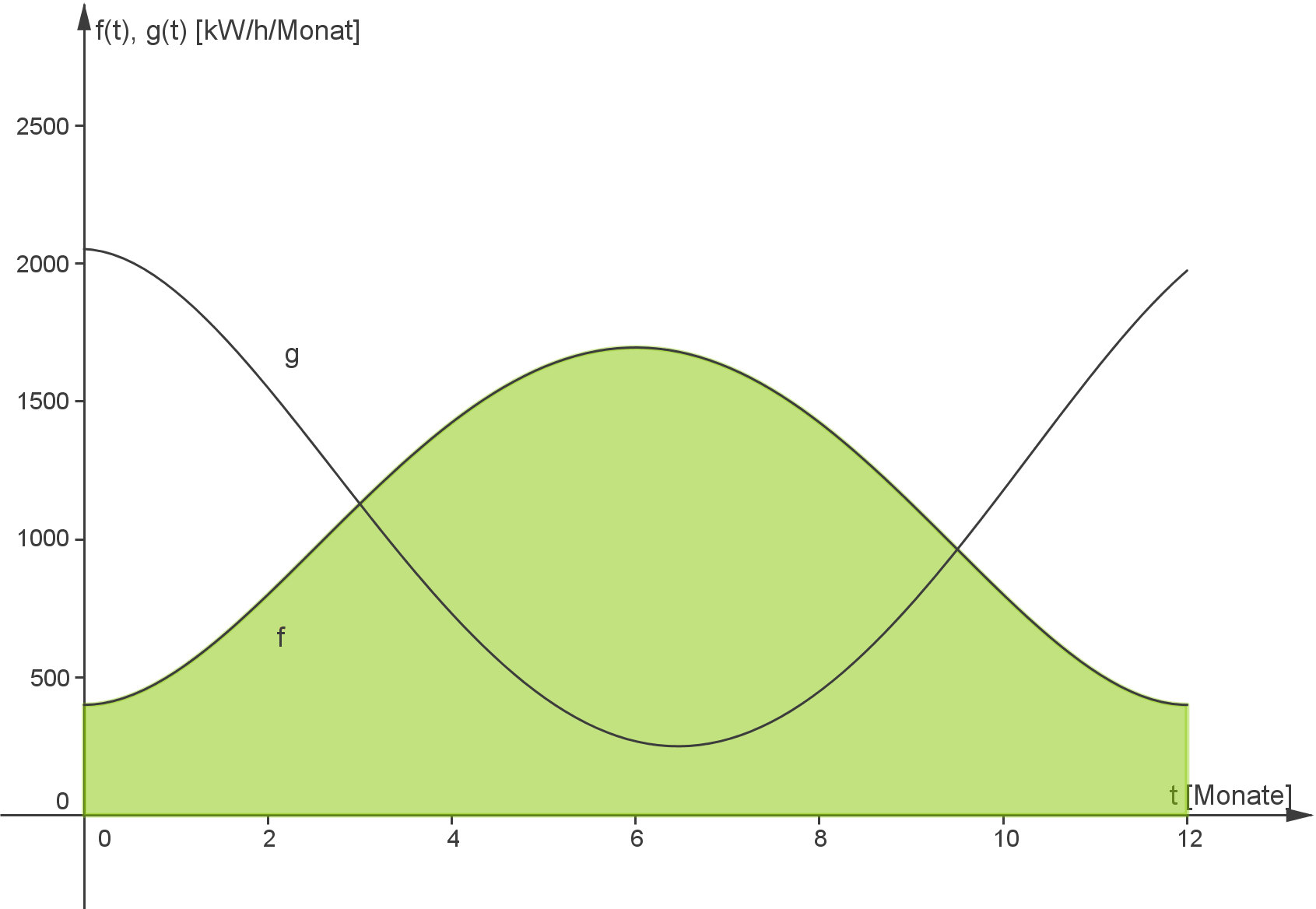
- Das zweite Integral
bestimmt den Inhalt der Fläche zwischen dem Graphen der Funktion
und dem Graphen der Funktion
im Intervall
:
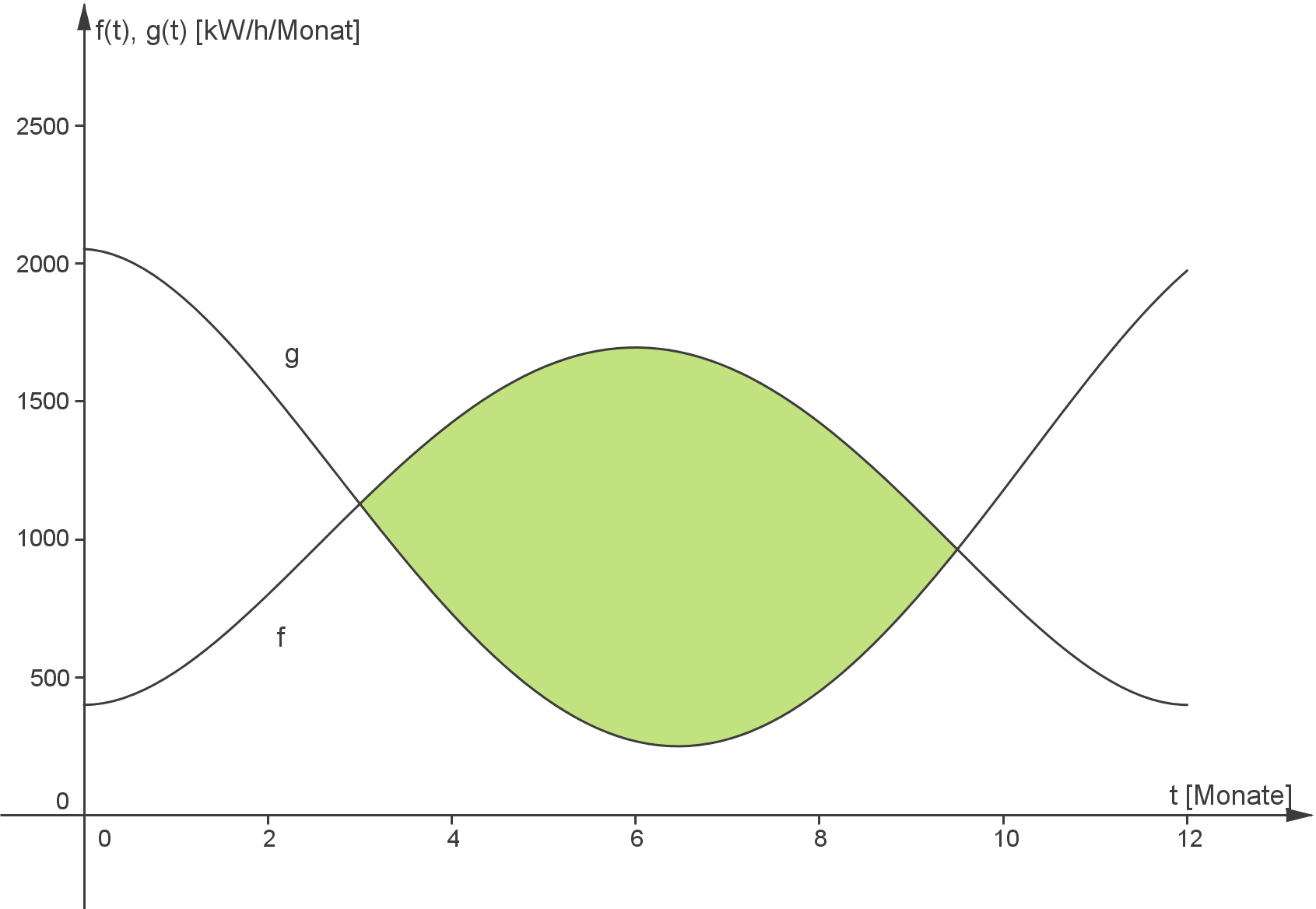

ist die über das gesamte Jahr von der Solaranlage erzeugte Energie.
ist der Energiebedarf der Familie über das gesamte Jahr.
ist die im Sommer erzeugte überschüssige Energie.
a) (1)
 Vergleich von
Vergleich von  und
und  im Sachzusammenhang
Hier sollst du die Graphen von
im Sachzusammenhang
Hier sollst du die Graphen von  und
und  im Sachzusammenhang vergleichen. Die Funktion
im Sachzusammenhang vergleichen. Die Funktion  modelliert die Leistung der Solaranlage, die Funktion
modelliert die Leistung der Solaranlage, die Funktion  den Leistungsbedarf der Familie. Du erkennst, dass in den Intervallen
den Leistungsbedarf der Familie. Du erkennst, dass in den Intervallen ![\(\left[0;3\right]\)](https://www.schullv.de/resources/formulas/e6ac5d60749307c17b05c9a262850c1a1312bb0bdac1077886594150a0f01657_light.svg) und
und ![\(\left[9,5;12\right]\)](https://www.schullv.de/resources/formulas/47d231a407dc5122a8184c20a6aacccc109aaeff05e0642aed51402f3d886a66_light.svg) der Graph der Funktion
der Graph der Funktion  oberhalb des Graphen von
oberhalb des Graphen von  liegt, im Intervall
liegt, im Intervall ![\(\left[3;9,5\right]\)](https://www.schullv.de/resources/formulas/a03ac5fe1f2ee83bfa4590b6a6c79fbf40a569515ebcc534bfeed1e72a1f310a_light.svg) ist es gerade andersrum und der Graph von
ist es gerade andersrum und der Graph von  liegt über dem Graphen von
liegt über dem Graphen von  . Die Graphen von
. Die Graphen von  und
und  verhalten sich gegenläufig um einen Mittelwert von ca.
verhalten sich gegenläufig um einen Mittelwert von ca.  .
Im Sachzusammenhang lässt sich dies so deuten, dass im Winter (Intervalle
.
Im Sachzusammenhang lässt sich dies so deuten, dass im Winter (Intervalle ![\(\left[0;3\right]\)](https://www.schullv.de/resources/formulas/e6ac5d60749307c17b05c9a262850c1a1312bb0bdac1077886594150a0f01657_light.svg) und
und ![\(\left[9,5;12\right]\)](https://www.schullv.de/resources/formulas/47d231a407dc5122a8184c20a6aacccc109aaeff05e0642aed51402f3d886a66_light.svg) ) ein hoher Bedarf an Energie besteht und die Solaranlage wenig Energie generiert. Es wird somit weniger Energie generiert als verbraucht. Im Sommer (Intervall
) ein hoher Bedarf an Energie besteht und die Solaranlage wenig Energie generiert. Es wird somit weniger Energie generiert als verbraucht. Im Sommer (Intervall ![\(\left[3;9,5\right]\)](https://www.schullv.de/resources/formulas/a03ac5fe1f2ee83bfa4590b6a6c79fbf40a569515ebcc534bfeed1e72a1f310a_light.svg) ) hingegen ist die Leistung der Solaranlage groß und der Bedarf an Energie niedrig. Hier wird nun mehr Energie generiert als verbraucht.
Um den Juni (
) hingegen ist die Leistung der Solaranlage groß und der Bedarf an Energie niedrig. Hier wird nun mehr Energie generiert als verbraucht.
Um den Juni ( ) ist die Leistung der Solaranlage maximal und der Leistungsbedarf minimal. Um den Jahreswechsel (
) ist die Leistung der Solaranlage maximal und der Leistungsbedarf minimal. Um den Jahreswechsel ( bzw.
bzw.  ) ist die Leistung der Solaranlage minimal und der Leistungsbedarf maximal.
(2)
) ist die Leistung der Solaranlage minimal und der Leistungsbedarf maximal.
(2)

 berechnen und im Sachzusammenhang interpretieren
Zuerst sollst du den Wert
berechnen und im Sachzusammenhang interpretieren
Zuerst sollst du den Wert  berechnen. Um die Werte
berechnen. Um die Werte  bzw.
bzw.  zu berechnen, setze jeweils
zu berechnen, setze jeweils  in die Funktionsgleichungen von
in die Funktionsgleichungen von  bzw.
bzw.  ein:
ein:
 Nun sollst du noch diesen Wert interpretieren.
Nun sollst du noch diesen Wert interpretieren.  repräsentiert hier die Leistung der Solaranlage zum Zeitpunkt
repräsentiert hier die Leistung der Solaranlage zum Zeitpunkt  , also zu Beginn des Jahres,
, also zu Beginn des Jahres,  den Leistungsbedarf zu Beginn des Jahres. Der Quotient dieser beiden Werte ist der Anteil an Leistungsbedarf, der von der Solaranlage gedeckt wird. Es wird also zu Beginn des Jahres
den Leistungsbedarf zu Beginn des Jahres. Der Quotient dieser beiden Werte ist der Anteil an Leistungsbedarf, der von der Solaranlage gedeckt wird. Es wird also zu Beginn des Jahres  des Leistungsbedarf von der Solaranlage gedeckt.
(3)
des Leistungsbedarf von der Solaranlage gedeckt.
(3)
 Zeigen, dass Leistung der Solaranlage dem Leistungsbedarf entspricht
Hier ist nun deine Aufgabe zu zeigen, dass die Leistung der Solaranlage und der Leistungsbedarf der Familie zu den Zeitpunkten
Zeigen, dass Leistung der Solaranlage dem Leistungsbedarf entspricht
Hier ist nun deine Aufgabe zu zeigen, dass die Leistung der Solaranlage und der Leistungsbedarf der Familie zu den Zeitpunkten  und
und  gleich sind. Berechne hierzu die beiden Funktionswerte
gleich sind. Berechne hierzu die beiden Funktionswerte  und
und  bzw.
bzw.  und
und  und überprüfe diese auf Gleichheit.
und überprüfe diese auf Gleichheit.
 Zeitpunkt
Zeitpunkt  :
:
![\(\begin{array}[t]{rll}
f(3)&=3^4-24\cdot 3^3 + 144\cdot 3^2 + 400 \\[5pt]
&=81-648+1.296+400=1.129\\[5pt]
g(3)&=-3^4 +26\cdot 3^3 -167,5 \cdot 3^2 -12,5 \cdot 3 +2.053 \\[5pt]
&=-81 + 702 - 1.507,5 - 37,5 + 2.053 =1.129
\end{array}\)](https://www.schullv.de/resources/formulas/48fc1f40397a9fd099ad26b52927ca2ef68eb5d1238e3b92e042c83ccb1e9638_light.svg) Somit gilt
Somit gilt  , also sind Leistung der Solaranlage und der Leistungsbedarf gleich.
, also sind Leistung der Solaranlage und der Leistungsbedarf gleich.
 Zeitpunkt
Zeitpunkt  :
:
![\(\begin{array}[t]{rll}
f(9,5)&={9,5}^4-24\cdot {9,5}^3 + 144\cdot {9,5}^2 + 400 \\[5pt]
&=8.145,0625 - 20.577 + 12.996 + 400 = 964,0625\\[5pt]
g(9,5)&=-{9,5}^4 +26\cdot {9,5}^3 -167,5 \cdot {9,5}^2 -12,5 \cdot 9,5 +2.053 \\[5pt]
&=-8.145,0625 + 22.291,75 - 15.116,875 - 118,75 + 2.053 = 964,0625
\end{array}\)](https://www.schullv.de/resources/formulas/700bb76a49f228d68e41aaa083f677d6be09064f0cc9f33e87eda91f42fb7a0a_light.svg) Somit gilt
Somit gilt  , also sind Leistung der Solaranlage und der Leistungsbedarf gleich.
, also sind Leistung der Solaranlage und der Leistungsbedarf gleich.
b) (1)
 Maximale Leistung der Solaranlage und deren Zeitpunkt bestimmen
Deine Aufgabe ist es den Zeitpunkt der maximalen Leistung der Solaranlage und den dazugehörigen Maximalwert zu bestimmen. Die Leistung der Solaranlage wird durch die Funktion
Maximale Leistung der Solaranlage und deren Zeitpunkt bestimmen
Deine Aufgabe ist es den Zeitpunkt der maximalen Leistung der Solaranlage und den dazugehörigen Maximalwert zu bestimmen. Die Leistung der Solaranlage wird durch die Funktion  beschrieben, also suchst du die Maximalstelle und den Maximalwert der Funktion
beschrieben, also suchst du die Maximalstelle und den Maximalwert der Funktion  . Diese kannst du per Hand oder mit deinem GTR bestimmen.
. Diese kannst du per Hand oder mit deinem GTR bestimmen.
 Lösungsweg A: Lösen per Hand
Eine Extremstelle einer Funktion ist durch die notwendige und hinreichende Bedingung bestimmt. Die Maximalstelle und den Maximalwert kannst du folgendermaßen berechnen:
Lösungsweg A: Lösen per Hand
Eine Extremstelle einer Funktion ist durch die notwendige und hinreichende Bedingung bestimmt. Die Maximalstelle und den Maximalwert kannst du folgendermaßen berechnen:
 bestimmen
bestimmen
![\(\begin{array}[t]{rll}
f(t)&=t^4-24 \cdot t^3 + 144 \cdot t^2 +400\\[10pt]
f‘(t)&=4\cdot t^3 - 24 \cdot \left(3 \cdot t^2\right) + 144 \cdot \left(2 \cdot t\right) \\[5pt]
&=4\cdot t^3 - 72\cdot t^2 + 288 \cdot t \\[10pt]
f‘‘(t)&=4\cdot \left(3\cdot t^2\right) - 72\cdot \left(2\cdot t\right) + 288 \\[5pt]
&=12 \cdot t^2 - 144 \cdot t +288
\end{array}\)](https://www.schullv.de/resources/formulas/ddff306844f10a6a5675de3a6c568c42bf729d1374e98c8bab4db0599d5a7b41_light.svg) 2. Schritt: Notwendiges Kriterium anwenden
Setze hier die erste Ableitungsfunktion von
2. Schritt: Notwendiges Kriterium anwenden
Setze hier die erste Ableitungsfunktion von  gleich Null und ermittle die Nullstellen:
gleich Null und ermittle die Nullstellen:
![\(\begin{array}[t]{rll}
0\stackrel{!}{=}&f‘(t) \\[5pt]
0=&4\cdot t^3 - 72\cdot t^2 + 288 \cdot t \\[5pt]
0=&t \cdot \left(4\cdot t^2 - 72\cdot t + 288 \right)
\end{array}\)](https://www.schullv.de/resources/formulas/0a65a939a0f3521e922f304ed500f03c0c644c0d825b4ebb5b9d44c96118a75e_light.svg) Nach dem Satz über das Nullprodukt kann ein Produkt nur Null sein, falls einer der Faktoren gleich Null ist. Somit sind hier die Möglichkeiten, dass
Nach dem Satz über das Nullprodukt kann ein Produkt nur Null sein, falls einer der Faktoren gleich Null ist. Somit sind hier die Möglichkeiten, dass  ist oder
ist oder  ist. Somit ist
ist. Somit ist  die erste mögliche Nullstelle. Betrachte nun den Term
die erste mögliche Nullstelle. Betrachte nun den Term  und ermittle die
und ermittle die  , für die er gleich Null ist. Dies kannst du entweder mit der Mitternachtsformel oder mit der PQ-Formel.
, für die er gleich Null ist. Dies kannst du entweder mit der Mitternachtsformel oder mit der PQ-Formel.
 Lösungsweg A1: PQ-Formel
Bringe dazu den Term auf die passende Form:
Lösungsweg A1: PQ-Formel
Bringe dazu den Term auf die passende Form:
![\(\begin{array}{rll}
0=&4\cdot t^2 - 72\cdot t + 288&\quad\mid\; :4 \\[5pt]
0=&t^2-18t+72
\end{array}\)](https://www.schullv.de/resources/formulas/1fd2c4300a6e6dbaa2a267eed18fa01e5bb95a38d98386ba26f577470936ad20_light.svg) Hier ist nun
Hier ist nun  und
und  :
:
![\(\begin{array}{rll}
t_{2,3} =& - \dfrac{-18}{2} \pm \sqrt{\left( {\frac{-18}{2}} \right)^2 - 72} \\[5pt]
t_{2,3} =& 9 \pm \sqrt {81 - 72}\\[5pt]
t_{2,3} =& 9 \pm \sqrt {9}\\[5pt]
t_{2,3} =& 9 \pm 3
\end{array}\)](https://www.schullv.de/resources/formulas/b5422c04a6072513b89517635122aba0637b136260857c4be860499b3f0343a1_light.svg) Die Extremstellen der Funktion
Die Extremstellen der Funktion  sind somit
sind somit  ,
,  und
und  .
.
 Lösungsweg A2: Mitternachtsformel
Du kannst die Mitternachtsformel hier direkt anwenden, wobei
Lösungsweg A2: Mitternachtsformel
Du kannst die Mitternachtsformel hier direkt anwenden, wobei  ,
,  und
und  :
:
![\(\begin{array}[t]{rll}
t_{2,3} =& \dfrac{{ - (-72) \pm \sqrt {(-72)^2 - 4 \cdot 4 \cdot 288} }}{{2\cdot 4}}\\[5pt]
t_{2,3} =&\dfrac{{ 72 \pm \sqrt {5.184 - 4.608} }}{{8}}\\[5pt]
t_{2,3} =&9 \pm \dfrac{\sqrt{576}}{8} \\[5pt]
t_{2,3} =&9 \pm \dfrac{24}{8} \\[5pt]
t_{2,3} =& 9 \pm 3
\end{array}\)](https://www.schullv.de/resources/formulas/4b4f4c6fa5edf278dca95a3cd418ee4633828361cbef2c1c1e048ad813e0ea5b_light.svg) Die Extremstellen der Funktion
Die Extremstellen der Funktion  sind somit
sind somit  ,
,  und
und  .
3. Schritt: Hinreichendes Kriterium überprüfen
Setze nun
.
3. Schritt: Hinreichendes Kriterium überprüfen
Setze nun  ,
,  und
und  in
in  ein:
ein:
 Zeitpunkt
Zeitpunkt  :
:
 , also ist
, also ist  Tiefstelle der Funktion
Tiefstelle der Funktion  .
.
 Zeitpunkt
Zeitpunkt  :
:
 , also ist
, also ist  Tiefstelle der Funktion
Tiefstelle der Funktion  .
.
 Zeitpunkt
Zeitpunkt  :
:
 , also ist
, also ist  die gesuchte Maximalstelle der Funktion
die gesuchte Maximalstelle der Funktion  .
4. Schritt: Maximalwert berechnen
Nun musst du noch den Maximalwert an der Stelle
.
4. Schritt: Maximalwert berechnen
Nun musst du noch den Maximalwert an der Stelle  berechnen. Setze dazu
berechnen. Setze dazu  in die Funktionsgleichung
in die Funktionsgleichung  ein:
ein:
![\(\begin{array}[t]{rll}
f(6)&=6^4-24 \cdot 6^3 +144 \cdot 6^2 +400 \\[5pt]
&=1.296 -5.184 + 5.184 +400= 1.696
\end{array}\)](https://www.schullv.de/resources/formulas/cba32a0c2c7e5e48b31e2ece09c772b4382bec77de09a3e79edf7a9312b78da0_light.svg) Damit ist die Leistung der Solaranlage zum Zeitpunkt
Damit ist die Leistung der Solaranlage zum Zeitpunkt  maximal und hat einen Maximalwert von
maximal und hat einen Maximalwert von  .
.
 Lösungsweg B: Lösen mit dem GTR
Wechsle mit deinem GTR in das Graph-Menü und speichere dort den Funktionsterm von
Lösungsweg B: Lösen mit dem GTR
Wechsle mit deinem GTR in das Graph-Menü und speichere dort den Funktionsterm von  . Hast du diesen dort gespeichert, gib unter
. Hast du diesen dort gespeichert, gib unter
 und
und  ein. Wechsle wieder in das Y=-Menü und lass dir den zugehörigen Graph über DRAW anzeigen.
Wähle dann unter
ein. Wechsle wieder in das Y=-Menü und lass dir den zugehörigen Graph über DRAW anzeigen.
Wähle dann unter
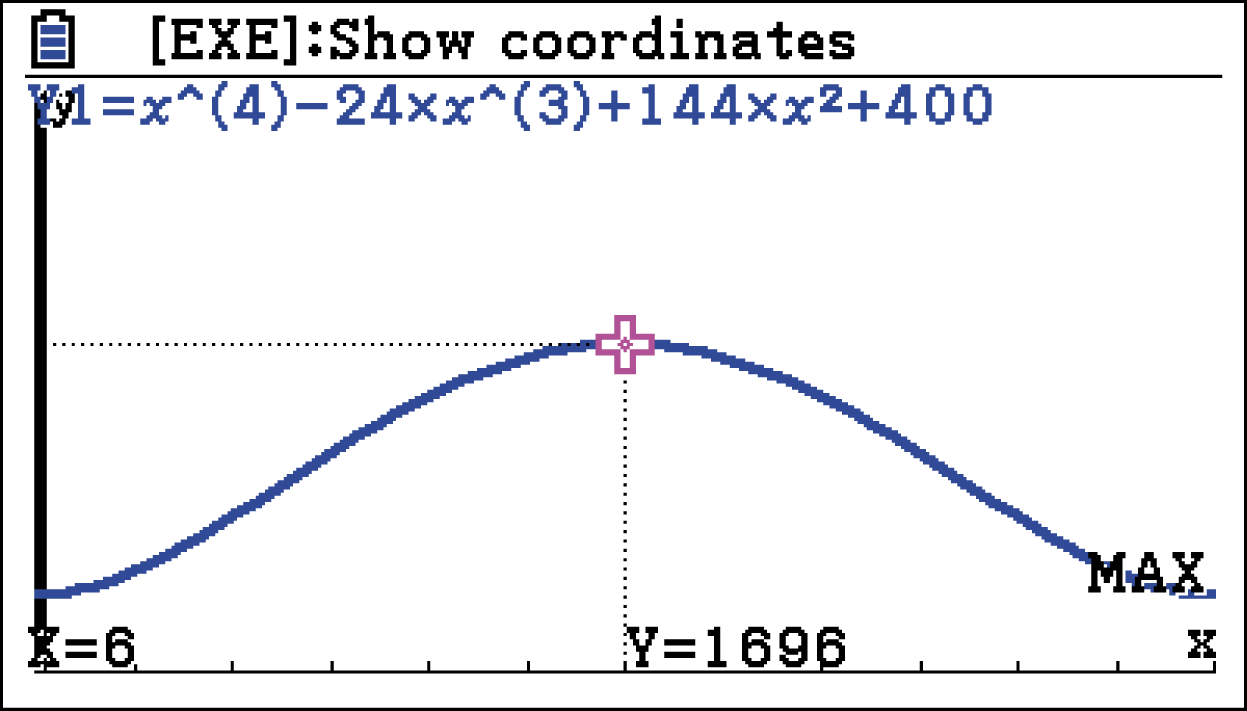 Damit ist die Leistung der Solaranlage zum Zeitpunkt
Damit ist die Leistung der Solaranlage zum Zeitpunkt  maximal und hat einen Maximalwert von
maximal und hat einen Maximalwert von  .
(2)
.
(2)
 Zeitpunkt der maximalen Abnahme des Leistungsbedarfs bestimmen
Gesucht ist der Zeitpunkt im Intervall
Zeitpunkt der maximalen Abnahme des Leistungsbedarfs bestimmen
Gesucht ist der Zeitpunkt im Intervall ![\([0;12]\)](https://www.schullv.de/resources/formulas/5ba9b38204a320e9433651393178f89e741e0a72de8e09a0201574090d0733c6_light.svg) , zu dem der durch
, zu dem der durch  beschriebene Leistungsbedarf am stärksten abnimmt. Dies kannst du auch folgendermaßen interpretieren:
Die Änderungsrate
beschriebene Leistungsbedarf am stärksten abnimmt. Dies kannst du auch folgendermaßen interpretieren:
Die Änderungsrate  beschreibt die Zu- oder Abnahme des Leistungsbedarf der Familie. Da der Zeitpunkt der stärksten Abnahme gesucht ist, erhältst du diesen durch das Bestimmen des Minimums der Änderungsrate
beschreibt die Zu- oder Abnahme des Leistungsbedarf der Familie. Da der Zeitpunkt der stärksten Abnahme gesucht ist, erhältst du diesen durch das Bestimmen des Minimums der Änderungsrate  . Leite also
. Leite also  ab und bestimme anschließend die Minimalstelle der Ableitung. Dieses kannst du per Hand oder mit deinem GTR bestimmen.
ab und bestimme anschließend die Minimalstelle der Ableitung. Dieses kannst du per Hand oder mit deinem GTR bestimmen.
 Lösungsweg A: Lösen per Hand
Eine Extremstelle einer Funktion ist durch die notwendige und hinreichende Bedingung bestimmt. Die Minimalstelle von
Lösungsweg A: Lösen per Hand
Eine Extremstelle einer Funktion ist durch die notwendige und hinreichende Bedingung bestimmt. Die Minimalstelle von  kannst du folgendermaßen berechnen:
kannst du folgendermaßen berechnen:
 bilden
bilden
![\(\begin{array}[t]{rll}
g(t)&=-t^4 + 26 \cdot t^3 - 167,5 \cdot t^2 -12,5 \cdot t + 2.053\\[10pt]
g‘(t)&=-\left(4\cdot t^3\right) + 26 \cdot \left(3 \cdot t^2\right) -167,5 \cdot \left(2 \cdot t\right) - 12,5\\[5pt]
&=-4\cdot t^3 + 78\cdot t^2 -335 \cdot t -12,5 \\[10pt]
g‘‘(t)&=-4\cdot \left(3\cdot t^2\right) + 78 \cdot \left(2\cdot t\right) - 335 \\[5pt]
&=-12 \cdot t^2 + 156 \cdot t -335 \\[10pt]
g‘‘‘(t)&=-12\cdot \left(2\cdot t\right) + 156 \\[5pt]
&=-24 \cdot t + 156
\end{array}\)](https://www.schullv.de/resources/formulas/97e55d68dc1e887ab038ee8b8abfe571d311ee01fedf0d6936b061be7c1d55de_light.svg) 2. Schritt: Notwendiges Kriteriumn anwenden
Setze hier die erste Ableitungsfunktion von
2. Schritt: Notwendiges Kriteriumn anwenden
Setze hier die erste Ableitungsfunktion von  , also
, also  , gleich Null und ermittle die Nullstellen:
, gleich Null und ermittle die Nullstellen:
![\(\begin{array}[t]{rll}
0\stackrel{!}{=}&g‘‘(t) \\[5pt]
0=&-12 \cdot t^2 + 156 \cdot t -335
\end{array}\)](https://www.schullv.de/resources/formulas/42f74cfec63f01683192ba9c98c59a9d8797a2af428efa08e821b2d59156608a_light.svg) Hier kannst du entweder die PQ-Formel oder die Mitternachtsformel verwenden, um die Nullstellen zu bestimmen.
Hier kannst du entweder die PQ-Formel oder die Mitternachtsformel verwenden, um die Nullstellen zu bestimmen.
 Lösungsweg A1: PQ-Formel
Bringe dazu den Term auf die passende Form:
Lösungsweg A1: PQ-Formel
Bringe dazu den Term auf die passende Form:
![\(\begin{array}{rll}
0=&-12 \cdot t^2 + 156 \cdot t -335 &\quad\mid\; :\left(-12\right) \\[5pt]
0=&t^2-13t+\dfrac{335}{12}
\end{array}\)](https://www.schullv.de/resources/formulas/52d4f38dfd7712e719ca1f64a493af096a971edbaecc3c38b39543fb8a1a909f_light.svg) Hier ist nun
Hier ist nun  und
und  :
:
![\(\begin{array}{rll}
t_{1,2} =& - \dfrac{-13}{2} \pm \sqrt{\left( {\frac{-13}{2}} \right)^2 - \frac{335}{12}} \\[5pt]
t_{1,2} =& \dfrac{13}{2} \pm \sqrt {\frac{169}{4} - \frac{335}{12}}\\[5pt]
t_{1,2} =& \dfrac{13}{2} \pm \sqrt {\frac{43}{3}}\\[5pt]
t_{1,2} =& 6,5 \pm 3,79
\end{array}\)](https://www.schullv.de/resources/formulas/dd1ec7a1318e2642ba8d0aebd164341b7385be0e0cb5dd3f13cb0615d3b05620_light.svg) Die Minimalstellen der ersten Ableitung
Die Minimalstellen der ersten Ableitung  sind somit
sind somit  und
und  .
.
 Lösungsweg A2: Mitternachtsformel
Du kannst die Mitternachtsformel hier direkt anwenden, wobei
Lösungsweg A2: Mitternachtsformel
Du kannst die Mitternachtsformel hier direkt anwenden, wobei  ,
,  und
und  :
:
![\(\begin{array}[t]{rll}
t_{1,2} =& \dfrac{{ - 156 \pm \sqrt {156^2 - 4 \cdot (-12) \cdot (-335)} }}{{2\cdot (-12)}}\\[5pt]
t_{1,2} =&\dfrac{{ 156 \pm \sqrt {24.336 - 16.080} }}{{24}}\\[5pt]
t_{1,2} =& \dfrac{13}{2} \pm \dfrac{\sqrt{8.256}}{24} \\[5pt]
t_{1,2} =& 6,5 \pm 3,79
\end{array}\)](https://www.schullv.de/resources/formulas/f39c725e9489b337082019b891b76f3e798c18d95bd4ed4a2e70ae75fffe68d0_light.svg) Die Minimalstellen der ersten Ableitung
Die Minimalstellen der ersten Ableitung  sind somit
sind somit  und
und  .
3. Schritt: Hinreichende Bedingung überprüfen
Setze nun
.
3. Schritt: Hinreichende Bedingung überprüfen
Setze nun  und
und  in
in  ein:
ein:
 Zeitpunkt
Zeitpunkt  :
:
 , also ist
, also ist  Maximalstelle der ersten Ableitung
Maximalstelle der ersten Ableitung  .
.
 Zeitpunkt
Zeitpunkt  :
:
 , also ist
, also ist  Minimalstelle der ersten Ableitung
Minimalstelle der ersten Ableitung  .
4. Schritt: Überprüfen der Randwerte
Berechne hier die Randwerte der ersten Ableitung
.
4. Schritt: Überprüfen der Randwerte
Berechne hier die Randwerte der ersten Ableitung  im Intervall
im Intervall ![\(\left[0;12\right]\)](https://www.schullv.de/resources/formulas/e2619fcaf7c9c53ab88bd0639e6ab76dffa4b2db3d6bb88b44a0b3e6c4238547_light.svg) und vergleiche diese mit dem Minimalwert. Setze dazu
und vergleiche diese mit dem Minimalwert. Setze dazu  ,
,  und
und  in
in  ein:
ein:
 Zeitpunkt
Zeitpunkt  :
:
 ist der Minimalwert der oben berechneten Minimalstelle der ersten Ableitung
ist der Minimalwert der oben berechneten Minimalstelle der ersten Ableitung  .
.
 Zeitpunkt
Zeitpunkt  :
:
 , also ist der Randwert
, also ist der Randwert  nicht Zeitpunkt maximaler Abnahme.
nicht Zeitpunkt maximaler Abnahme.
 Zeitpunkt
Zeitpunkt  :
:
 , also ist der Randwert
, also ist der Randwert  nicht Zeitpunkt maximaler Abnahme.
Der Leistungsbedarf nimmt somit zum Zeitpunkt
nicht Zeitpunkt maximaler Abnahme.
Der Leistungsbedarf nimmt somit zum Zeitpunkt  am stärksten ab.
am stärksten ab.
 Lösungsweg B: Lösen mit dem GTR
Berechne wie im Lösungsweg A die erste Ableitung
Lösungsweg B: Lösen mit dem GTR
Berechne wie im Lösungsweg A die erste Ableitung  . Wechsle anschließend mit deinem GTR in das Y=-Menü und speichere dort den Funktionsterm von
. Wechsle anschließend mit deinem GTR in das Y=-Menü und speichere dort den Funktionsterm von  . Hast du diesen dort gespeichert, gib unter
. Hast du diesen dort gespeichert, gib unter
 und
und  ein. Wechsle wieder in das Y=-Menü und lass dir den zugehörigen Graph über DRAW anzeigen.
Wähle dann unter
ein. Wechsle wieder in das Y=-Menü und lass dir den zugehörigen Graph über DRAW anzeigen.
Wähle dann unter
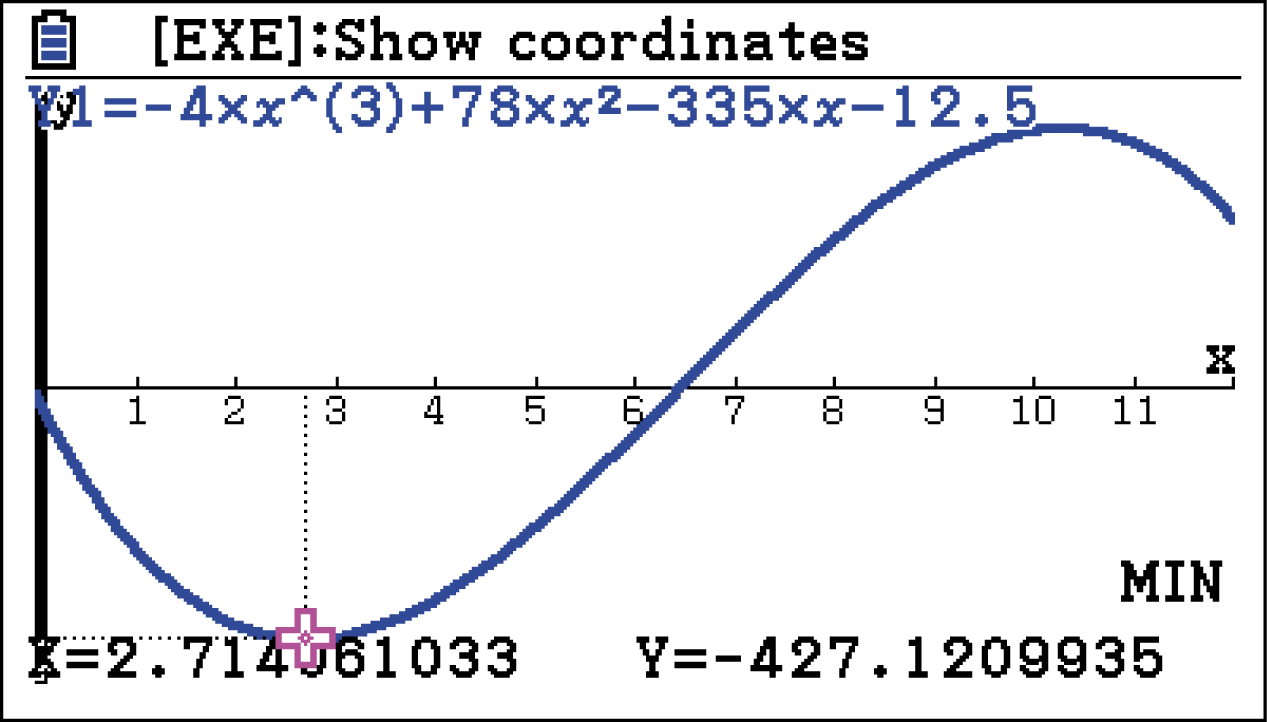 Also besitzt die Funktion
Also besitzt die Funktion  an der Stelle
an der Stelle  ein Minimum. Somit ist
ein Minimum. Somit ist  der Zeitpunkt im Intervall
der Zeitpunkt im Intervall ![\([0;12]\)](https://www.schullv.de/resources/formulas/5ba9b38204a320e9433651393178f89e741e0a72de8e09a0201574090d0733c6_light.svg) , an dem der Leistungsbedarf der Familie innerhalb dieses Kalenderjahres am stärksten abnimmt.
, an dem der Leistungsbedarf der Familie innerhalb dieses Kalenderjahres am stärksten abnimmt.
- Bestimme die erste und zweite Ableitung von
.
- Wende das notwendige Kriterium an. Für eine potenzielle Extremstelle
gilt:
Setze also
und löse nach
auf, um die möglichen Extremstellen zu bestimmen.
- Hinreichendes Kriterium überprüfen. Ist
für eine potenzielle Extremstelle
, so handelt es sich bei
um eine Maximalstelle. Setze die potenziellen Extremstellen in die zweite Ableitung ein und überprüfe das Ergebnis auf sein Vorzeichen.
- Den Maximalwert kannst du nun bestimmen, indem du die Maximalstelle in die Funktionsgleichung von
einsetzt.
SHIFT  F3 (V-Window)
F3 (V-Window)
die Intervallgrenzen
SHIFT  F5 (G-Solv)
F5 (G-Solv)  F2 (MAX)
F2 (MAX)
den Befehl zum Bestimmen des Maximums aus.

- Bestimme die erste, zweite und dritte Ableitung von
.
- Wende das notwendige Kriterium an. Für eine potenzielle Extremstelle
der Funktion
gilt:
Setze also
und löse nach
auf, um die möglichen Extremstellen zu bestimmen.
- Hinreichendes Kriterium überprüfen. Ist
für eine potenzielle Extremstelle
, so handelt es sich bei
um eine Minimalstelle. Setze die potenziellen Extremstellen in die dritte Ableitung ein und überprüfe das Ergebnis auf sein Vorzeichen.
- Überprüfe nun noch die Randwerte.
Berechne dazu die Funktionswerte
und
und vergleiche sie mit dem vorher berechneten Minimawert.
SHIFT  F3 (V-Window)
F3 (V-Window)
die Intervallgrenzen
SHIFT  F5 (G-Solv)
F5 (G-Solv)  F3 (MIN)
F3 (MIN)
den Befehl zum Bestimmen des Minimums aus.

c) (1)
 Stammfunktion
Stammfunktion  von
von  bestimmen
Hier ist es deine Aufgabe eine Stammfunktion
bestimmen
Hier ist es deine Aufgabe eine Stammfunktion  von
von  zu bestimmen. Integriere dazu die Funktion
zu bestimmen. Integriere dazu die Funktion  :
:
![\(\begin{array}[t]{rll}
\displaystyle\int_{}^{}g(t)\;\mathrm dt&=\displaystyle\int_{}^{}-t^4+26t^3-167,5t^2-12,5t+2.053\;\mathrm dt \\[5pt]
&=-\dfrac{1}{5}t^5+\dfrac{1}{4}\cdot 26t^4- \dfrac{1}{3}\cdot 167,5t^3-\dfrac{1}{2}\cdot12,5t^2+2.053 t +c\\[5pt]
&=-\dfrac{1}{5}t^5+\dfrac{13}{2}t^4- \dfrac{335}{6}t^3-\dfrac{25}{4}t^2+2.053 t +c
\end{array}\)](https://www.schullv.de/resources/formulas/bcfbe452516fa24ea3d9ac5d54d1fe33a7b26ae59e360b7482fbd1e34b9b3966_light.svg) Für
Für  ist
ist  eine Stammfunktion von
eine Stammfunktion von  .
.
 Berechnen des Energiebedarfs der Familie
Nach Aufgabenstellung ist durch das Integral
Berechnen des Energiebedarfs der Familie
Nach Aufgabenstellung ist durch das Integral  der Energiebedarf der Familie im Zeitintervall
der Energiebedarf der Familie im Zeitintervall ![\([a;b]\)](https://www.schullv.de/resources/formulas/e84e12d6ffce2d83a82ceef8cfb5eb14688a4f4cce00a0d08d5357e2c6858142_light.svg) gegeben. Das Zeitintervall
gegeben. Das Zeitintervall ![\([0;12]\)](https://www.schullv.de/resources/formulas/5ba9b38204a320e9433651393178f89e741e0a72de8e09a0201574090d0733c6_light.svg) beschreibt hier das Kalenderjahr. Somit musst du das Integral
beschreibt hier das Kalenderjahr. Somit musst du das Integral  berechnen. Dieses kannst du per Hand oder mit deinem GTR berechnen.
berechnen. Dieses kannst du per Hand oder mit deinem GTR berechnen.
 Lösungsweg A: Per Hand
Benutze hierzu den Hauptsatz der Integralrechnung und die zuvor berechnete Stammfunktion
Lösungsweg A: Per Hand
Benutze hierzu den Hauptsatz der Integralrechnung und die zuvor berechnete Stammfunktion  :
:
![\(\begin{array}[t]{rll}
\displaystyle\int_{0}^{12}g(t)\;\mathrm dt&=G(12)-G(0)\\[5pt]
&= \left(-\dfrac{1}{5}\cdot 12^5+\dfrac{13}{2}\cdot 12^4- \dfrac{335}{6}\cdot 12^3-\dfrac{25}{4}\cdot 12^2+2.053\cdot 12\right) - 0 \\[5pt]
&=-49.766,4 + 134.784 - 96.480 - 900 + 24.636 \\[5pt]
&=12.273,6
\end{array}\)](https://www.schullv.de/resources/formulas/5e88fdf679802e4bd1935ae3bce53399fb03063d48520859bb05f563a571d9db_light.svg) Der Energiebedarf der Familie für das Kalenderjahr beträgt
Der Energiebedarf der Familie für das Kalenderjahr beträgt  kWh.
kWh.
 Lösungsweg B: Lösen mit dem GTR
Wechsle mit deinem GTR in das Y=-Menü und speichere dort den Funktionsterm von
Lösungsweg B: Lösen mit dem GTR
Wechsle mit deinem GTR in das Y=-Menü und speichere dort den Funktionsterm von  . Hast du diesen dort gespeichert, dann lass dir den zugehörigen Graph über DRAW anzeigen.
Bestimme dann über
. Hast du diesen dort gespeichert, dann lass dir den zugehörigen Graph über DRAW anzeigen.
Bestimme dann über
 in den Grenzen des Intervalls
in den Grenzen des Intervalls ![\(\left[0;12\right]\)](https://www.schullv.de/resources/formulas/e2619fcaf7c9c53ab88bd0639e6ab76dffa4b2db3d6bb88b44a0b3e6c4238547_light.svg) .
.
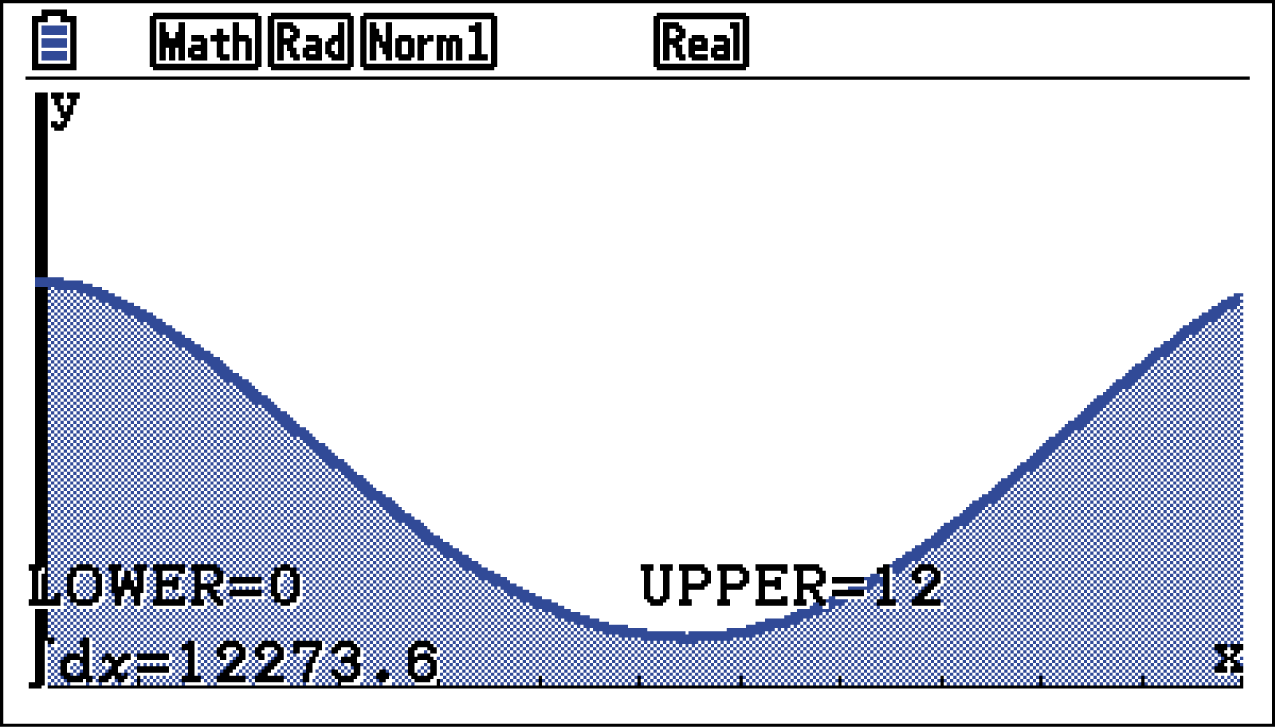 Der Energiebedarf der Familie für das Kalenderjahr beträgt
Der Energiebedarf der Familie für das Kalenderjahr beträgt  kWh.
(2)
kWh.
(2)
 Berechnen der Energie, die zum Heizen des Pools zur Verfügung steht
Der Pool wird mit der Energie geheizt, welche den Bedarf der Familie übersteigt. Dieser Leistungsüberschuss ist gerade die Differenz zwischen der von der Solaranlage erzeugten Leistung und dem Leistungsbedarf der Familie. Zum Zeitpunkt
Berechnen der Energie, die zum Heizen des Pools zur Verfügung steht
Der Pool wird mit der Energie geheizt, welche den Bedarf der Familie übersteigt. Dieser Leistungsüberschuss ist gerade die Differenz zwischen der von der Solaranlage erzeugten Leistung und dem Leistungsbedarf der Familie. Zum Zeitpunkt  ist der Leistungsüberschuss somit durch
ist der Leistungsüberschuss somit durch  gegeben.
Die überschüssige Energie im Intervall
gegeben.
Die überschüssige Energie im Intervall ![\(\left[3;9,5\right]\)](https://www.schullv.de/resources/formulas/a03ac5fe1f2ee83bfa4590b6a6c79fbf40a569515ebcc534bfeed1e72a1f310a_light.svg) kannst du durch das Integral über den Leistungsüberschuss auf dem Intervall
kannst du durch das Integral über den Leistungsüberschuss auf dem Intervall ![\(\left[3;9,5\right]\)](https://www.schullv.de/resources/formulas/a03ac5fe1f2ee83bfa4590b6a6c79fbf40a569515ebcc534bfeed1e72a1f310a_light.svg) berechnen. Gesucht ist somit das Integral:
$
berechnen. Gesucht ist somit das Integral:
$ $
Berechne also zuerst
$
Berechne also zuerst  . Danach kannst du das Integral per Hand oder mit deinem GTR bestimmen.
1. Schritt:
. Danach kannst du das Integral per Hand oder mit deinem GTR bestimmen.
1. Schritt:  berechnen
berechnen
![\(\begin{array}[t]{rll}
f(t)-g(t)&= \left(t^4-24 \cdot t^3 + 144 \cdot t^2 +400\right)-\left(-t^4 + 26 \cdot t^3 - 167,5 \cdot t^2 -12,5 \cdot t + 2.053\right) \\[5pt]
&=2\cdot t^4 - 50 \cdot t^3 + 311,5 \cdot t^2 +12,5 \cdot t -1.653
\end{array}\)](https://www.schullv.de/resources/formulas/d2483ef86d2852a157eb92c6a4e760587ca543b99a93ac46fe665e60f5fc78c4_light.svg)
 Lösungsweg A: Per Hand
Bestimme nun eine Stammfunktion
Lösungsweg A: Per Hand
Bestimme nun eine Stammfunktion  und berechne damit das Integral
und berechne damit das Integral  .
2. Schritt: Stammfunktion
.
2. Schritt: Stammfunktion  bestimmen
bestimmen
![\(\begin{array}[t]{rll}
\displaystyle\int_{}^{} \left(f(t)-g(t)\right) \;\mathrm dt&=\displaystyle\int_{}^{}2\cdot t^4 - 50 \cdot t^3 + 311,5 \cdot t^2 +12,5 \cdot t -1.653 \;\mathrm dt\\[5pt]
&=\dfrac{1}{5}\cdot 2t^5-\dfrac{1}{4}\cdot 50t^4+ \dfrac{1}{3}\cdot 311,5t^3+\dfrac{1}{2}\cdot12,5t^2-1.653 t +c\\[5pt]
&=\dfrac{2}{5}t^5-\dfrac{25}{2}t^4+ \dfrac{623}{6}t^3 +\dfrac{25}{4}t^2-1.653 t +c
\end{array}\)](https://www.schullv.de/resources/formulas/2ca820772fc352cb9528f2e91c366e1dc15c04ea40f4676f918026308640ec63_light.svg) Wähle
Wähle  und damit ist
und damit ist  eine Stammfunktion von
eine Stammfunktion von  .
3. Schritt: Integral
.
3. Schritt: Integral  berechnen
berechnen
![\(\begin{array}[t]{rll}
\displaystyle\int_{3}^{9,5} \left(f(t)-g(t)\right) \;\mathrm dt&= (F-G)(9,5)-(F-G)(3)\\[5pt]
&=\left(\dfrac{2}{5}\cdot 9,5^5-\dfrac{25}{2}\cdot 9,5^4+ \dfrac{623}{6}\cdot 9,5^3+\dfrac{25}{4}\cdot 9,5^2-1.653 \cdot 9,5\right) \\[5pt]
&- \left(\dfrac{2}{5}\cdot 3^5-\dfrac{25}{2}\cdot 3^4+ \dfrac{623}{6}\cdot 3^3+\dfrac{25}{4}\cdot 3^2-1.653 \cdot 3\right)\\[5pt]
&= 3.022,62 - \left(-3014,55\right)\\[5pt]
&= 3.022,62 + 3014,55\\[5pt]
&= 6.037,17
\end{array}\)](https://www.schullv.de/resources/formulas/0c034dfdb0375b8556fd466c25adb545f141b2477c3fb22a5b431bf1e45bb1ab_light.svg) Der Familie stehen somit
Der Familie stehen somit  kWh Energie zum Heizen des Pools zur Verfügung.
kWh Energie zum Heizen des Pools zur Verfügung.
 Lösungsweg B: Lösen mit dem GTR
Wechsle mit deinem GTR in das Y=-Menü und speichere dort den Funktionsterm von
Lösungsweg B: Lösen mit dem GTR
Wechsle mit deinem GTR in das Y=-Menü und speichere dort den Funktionsterm von  . Hast du die Funktionen
. Hast du die Funktionen  und
und  bereits gespeichert, so kannst du die Differenz auch über
bereits gespeichert, so kannst du die Differenz auch über
 in den Grenzen des Intervalls
in den Grenzen des Intervalls ![\(\left[3;9,5\right]\)](https://www.schullv.de/resources/formulas/a03ac5fe1f2ee83bfa4590b6a6c79fbf40a569515ebcc534bfeed1e72a1f310a_light.svg) .
.
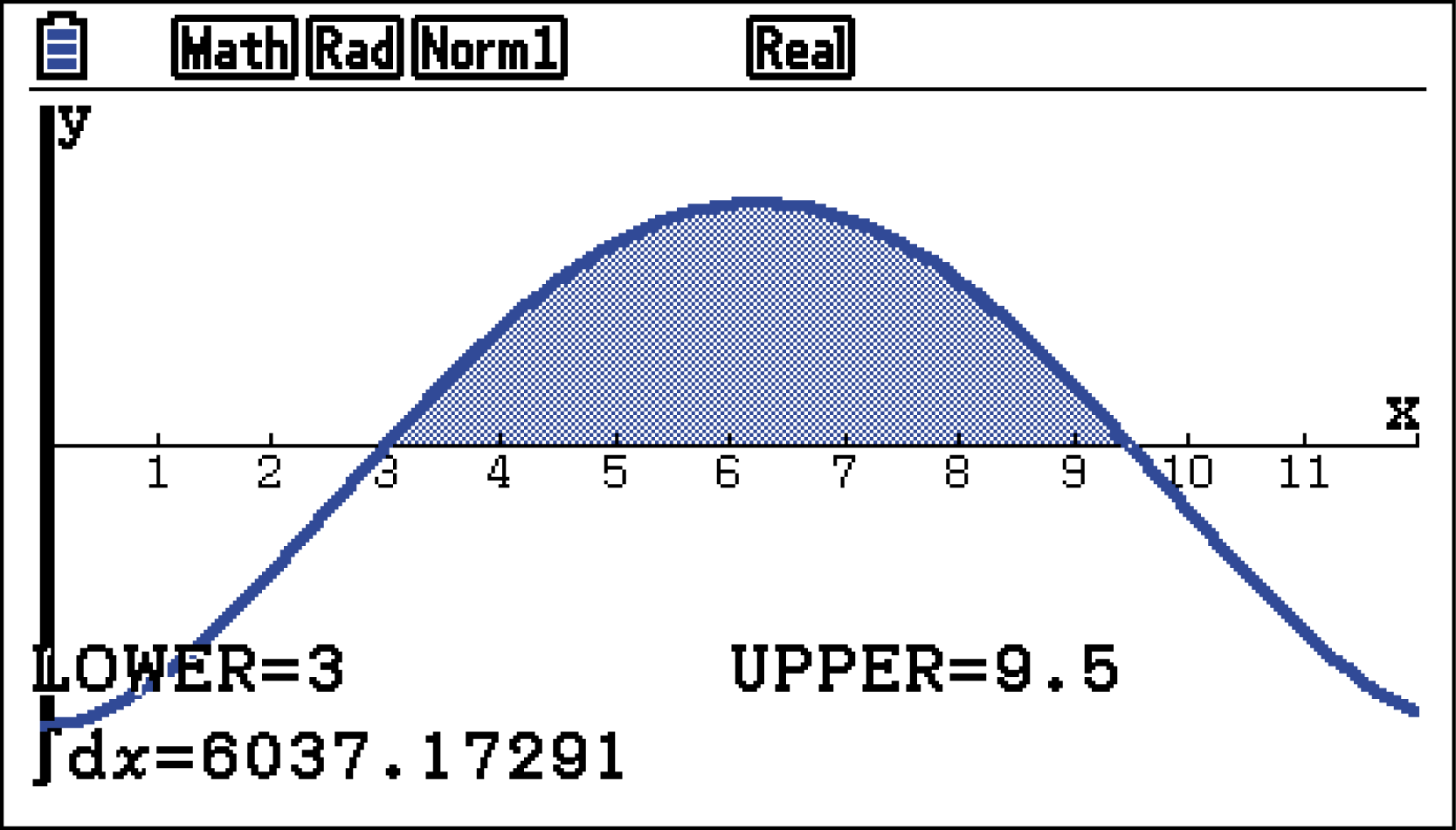 Der Familie stehen somit
Der Familie stehen somit  kWh Energie zum Heizen des Pools zur Verfügung.
(3)
kWh Energie zum Heizen des Pools zur Verfügung.
(3)
 Fläche skizzieren
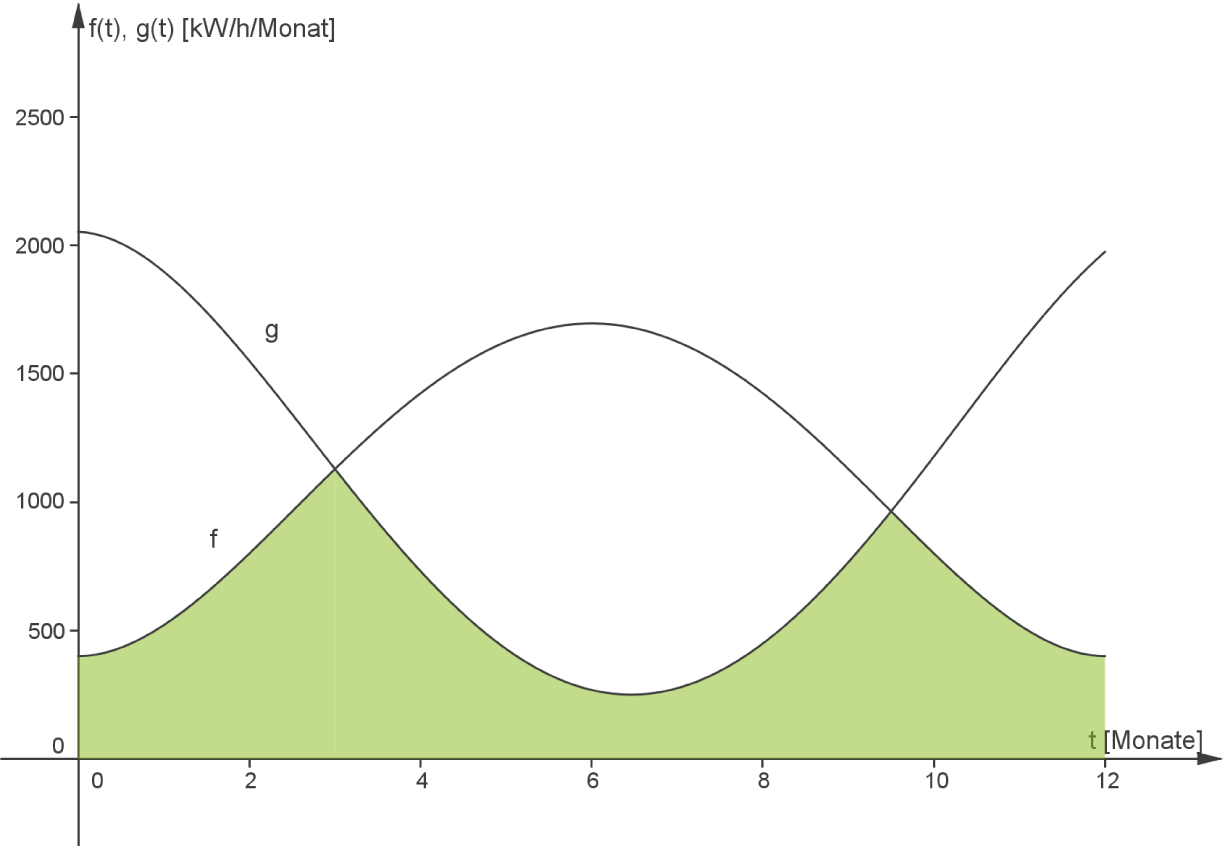
Deine Aufgabe ist es, die Fläche zu skizzieren, welche durch den Zähler des Bruches bestimmt wird. Der Zähler lautet:
Fläche skizzieren
Deine Aufgabe ist es, die Fläche zu skizzieren, welche durch den Zähler des Bruches bestimmt wird. Der Zähler lautet:
 Betrachte zuerst die einzelnen Terme des Zählers:
Betrachte zuerst die einzelnen Terme des Zählers:
![\([0;3]\)](https://www.schullv.de/resources/formulas/989ef35ddb608f4befc7b703f6465b5cf517e676c006489beb40101fdaaecf76_light.svg) und
und ![\([9,5;12]\)](https://www.schullv.de/resources/formulas/49df986b392bead3550143bb8b9dc9d0d0552400a195b44330c841b4a9be9e4b_light.svg) bleibt die erste Fläche unverändert. Im Intervall
bleibt die erste Fläche unverändert. Im Intervall ![\([3;9,5]\)](https://www.schullv.de/resources/formulas/595081264c02f7af17ad1e595d0a2048c633145a0eebe49dc0c880beccea2075_light.svg) wird von der Fläche unter dem Graphen von
wird von der Fläche unter dem Graphen von  die Fläche zwischen den Graphen von
die Fläche zwischen den Graphen von  und
und  abgezogen. Du erhältst die Fläche unter dem Graphen von
abgezogen. Du erhältst die Fläche unter dem Graphen von  . Insgesamt ergibt sich die unten eingezeichnete Fläche:
. Insgesamt ergibt sich die unten eingezeichnete Fläche:
 Interpretation der Berechnung im Sachzusammenhang
Mache dir hier zuerst klar, was die drei Integrale beschreiben. Dabei helfen dir der Aufgabentext und die Aufgabe c)(2).
Interpretation der Berechnung im Sachzusammenhang
Mache dir hier zuerst klar, was die drei Integrale beschreiben. Dabei helfen dir der Aufgabentext und die Aufgabe c)(2).
 Dies bedeutet, dass die Solaranlage über das ganze Jahr ca.
Dies bedeutet, dass die Solaranlage über das ganze Jahr ca.  des Gesamtbedarfs der Familie deckt.
des Gesamtbedarfs der Familie deckt.
SHIFT  F5 (G-Solv)
F5 (G-Solv)  F6
F6  F3 (
F3 ( dx)
dx)  F1 (
F1 ( dx)
dx)
das Integral über 
VARS  F4 (GRAPH)
F4 (GRAPH) 
und die entsprechenden Bezeichnungen berechnen. Lass dir dann den zugehörigen Graph über DRAW anzeigen.
Bestimme dann über
SHIFT  F5 (G-Solv)
F5 (G-Solv)  F6
F6  F3 (
F3 ( dx)
dx)  F1 (
F1 ( dx)
dx)
das Integral über 
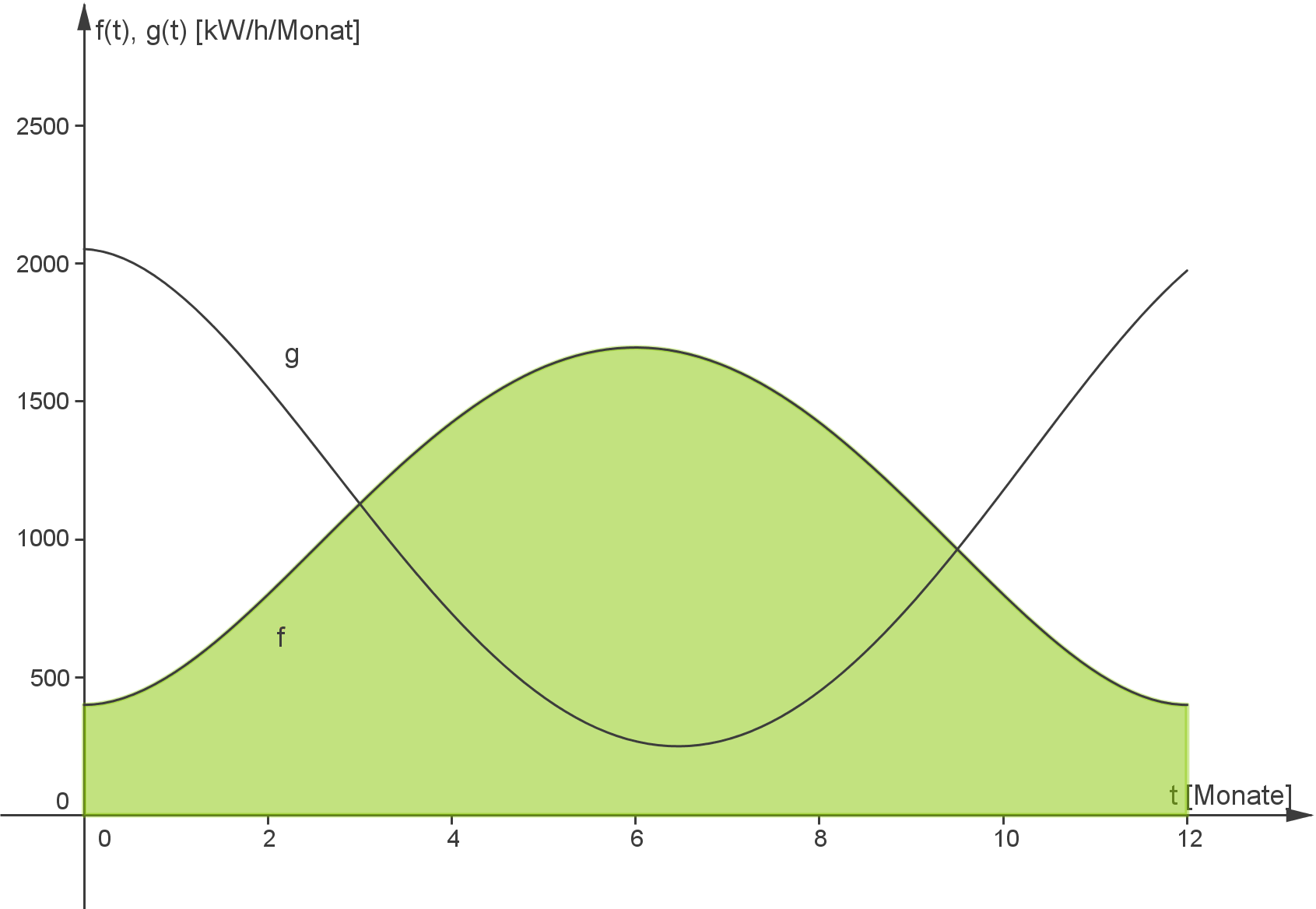
- Das erste Integral
entspricht dem Inhalt der Fläche zwischen dem Graphen der Funktion
und der
-Achse im Intervall
:
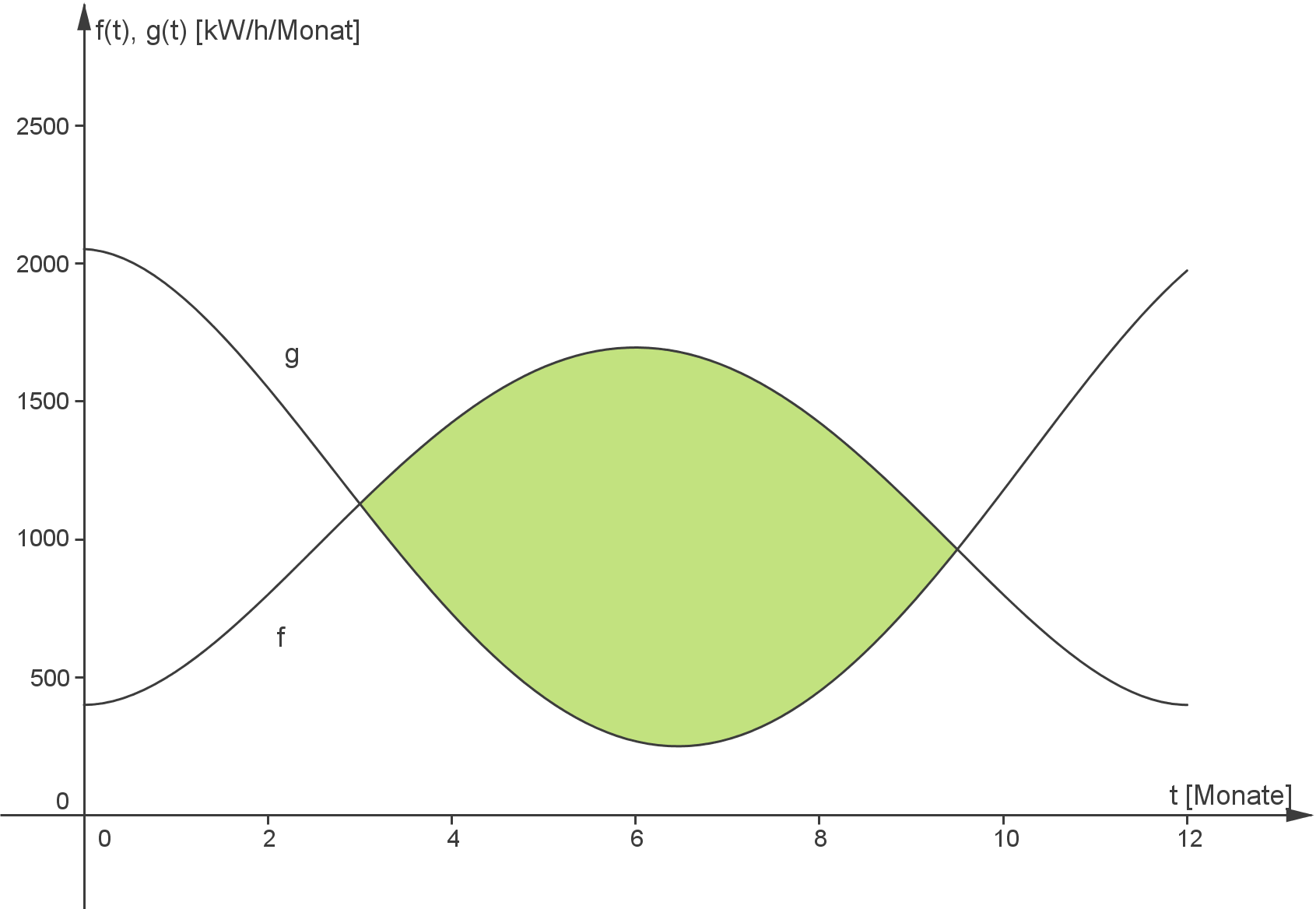
- Das zweite Integral
bestimmt den Inhalt der Fläche zwischen dem Graphen der Funktion
und dem Graphen der Funktion
im Intervall
:

ist die über das gesamte Jahr von der Solaranlage erzeugte Energie.
ist der Energiebedarf der Familie über das gesamte Jahr.
ist die im Sommer erzeugte überschüssige Energie.