Vektorielle Geometrie
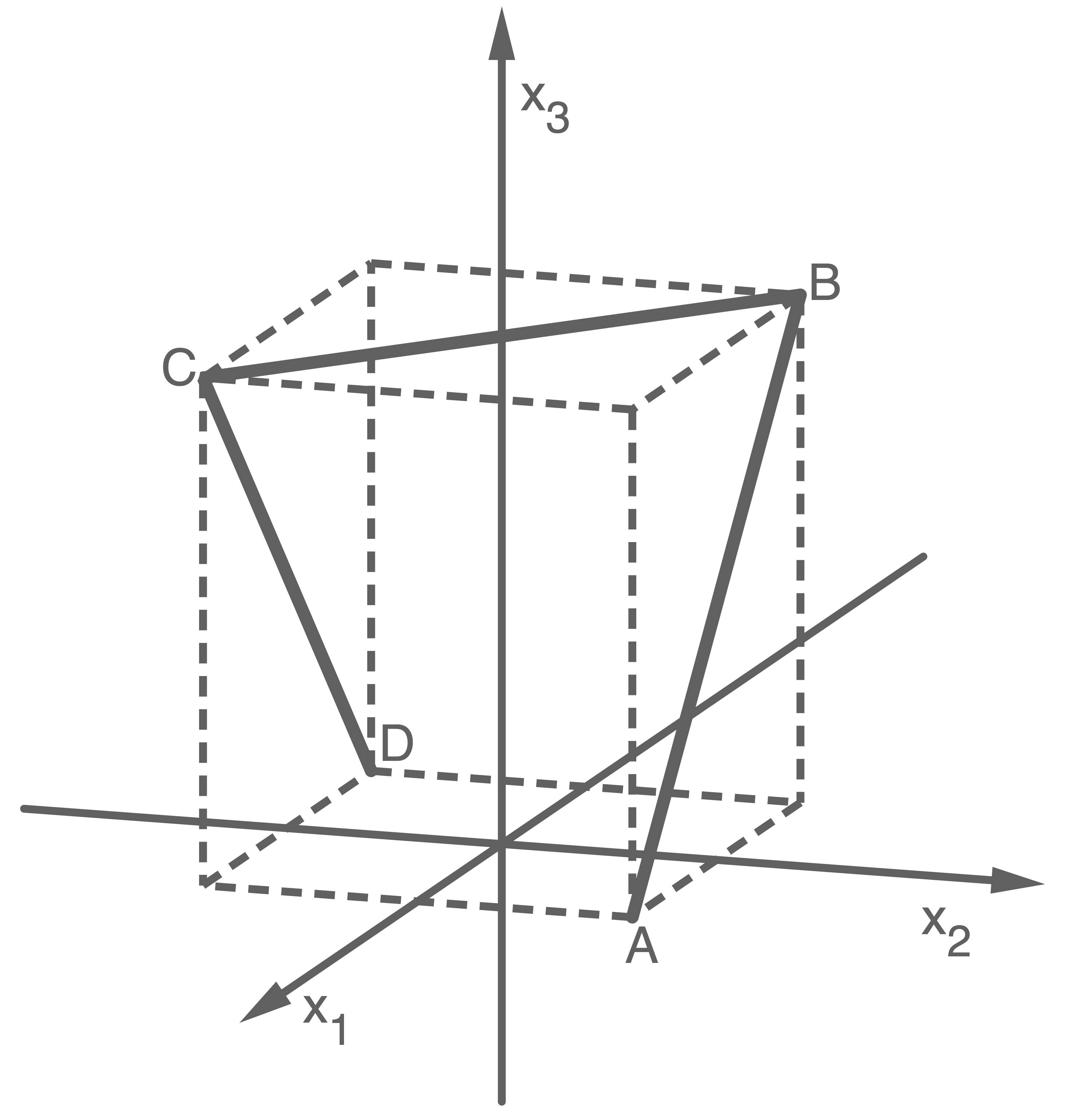
Die Abbildung zeigt das sogenannte Saarpolygon, ein im Inneren begehbares Denkmal zur Erinnerung an den stillgelegten Kohlebergbau im Saarland. Das Saarpolygon kann in einem Koordinatensystem modellhaft durch den Streckenzug dargestellt werden, der aus den drei Strecken 
und 
mit 
und 
besteht.
und 
sind Eckpunkte eines Quaders. Eine Längeneinheit im Koordinatensystem entspricht einem Meter in der Wirklichkeit.
und mit und besteht.
und sind Eckpunkte eines Quaders. Eine Längeneinheit im Koordinatensystem entspricht einem Meter in der Wirklichkeit.
a)
Begründe, dass die Punkte 
und symmetrisch bezüglich der 
-Achse liegen.
und symmetrisch bezüglich der -Achse liegen.
(3 Punkte)
b)
Berechne die Länge des Streckenzugs in der Wirklichkeit.
(3 Punkte)
c)
Die Ebene 
enthält die Punkte und und teilt den Quader in zwei Teilkörper. Bestimme das Verhältnis der Volumina der beiden Teilkörper, ohne die Volumina zu berechnen.
enthält die Punkte und und teilt den Quader in zwei Teilkörper. Bestimme das Verhältnis der Volumina der beiden Teilkörper, ohne die Volumina zu berechnen.
(4 Punkte)
d)
Das Saarpolygon wird von verschiedenen Positionen aus betrachtet. Die Abbildungen 1 und 2 stellen das Saarpolygon für zwei Positionen schematisch dar.
Gib zu jeder der beiden Abbildungen einen möglichen Vektor an, der die zu der Position gehörige Blickrichtung beschreibt.
Stelle das Saarpolygon schematisch für eine Betrachtung von oben dar.
Abb. 1
Abb. 2
(5 Punkte)
e)
Der Punkt 
liegt innerhalb des Quaders und hat von den drei Strecken 
und den gleichen Abstand. Das folgende Gleichungssystem liefert den Wert von 
![\(\overrightarrow{OQ}=\pmatrix{11\\11\\0}+t\cdot\pmatrix{-22\\0\\28},t\in\left[0;1\right]\)](https://www.schullv.de/resources/formulas/bc430c4c1933557c7d10bd376fe01a7682a304d0326f4b7403cd218103ca933a_light.svg)
Erläutere die Überlegungen, die diesem Vorgehen zur Bestimmung des Wertes von 
zugrunde liegen.
liegt innerhalb des Quaders und hat von den drei Strecken und den gleichen Abstand. Das folgende Gleichungssystem liefert den Wert von
Erläutere die Überlegungen, die diesem Vorgehen zur Bestimmung des Wertes von zugrunde liegen.
(5 Punkte)
(20 Punkte)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
Sowohl die 
-Koordinaten als auch die 
-Koordinaten von und unterscheiden sich nur in ihren Vorzeichen, die 
-Koordinaten stimmen überein. Folglich liegen die Punkte und symmetrisch bezüglich der -Achse.
-Koordinaten als auch die -Koordinaten von und unterscheiden sich nur in ihren Vorzeichen, die -Koordinaten stimmen überein. Folglich liegen die Punkte und symmetrisch bezüglich der -Achse.
b)
![\(\begin{array}[t]{rll}
|\overline{A B}|&=& |\overline{C D}|& \\[5pt]
&=&\left| \pmatrix{-11-11\\11-11\\28-0} \right| & \\[5pt]
&=& \left| \pmatrix{-22\\0\\28} \right|& \\[5pt]
&\approx& 35,61 \; [\text{m}]
\end{array}\)](https://www.schullv.de/resources/formulas/bcc89f40e1425d50439f93b56e82e94c051f6bf97d47269bbba3ab58213ee807_light.svg)
![\(\begin{array}[t]{rll}
|\overline{B C}|&=& \left| \pmatrix{11-(-11)\\-11-11\\28-28} \right|&\\[5pt]
&=& \left| \pmatrix{22\\-22\\0} \right|&\\[5pt]
&\approx& 31,11 \; [\text{m}]
\end{array}\)](https://www.schullv.de/resources/formulas/beebb732bdb82b82912756579b08e90641fee2fc70cf28e8260e9262d82afdb5_light.svg)
![\(\begin{array}[t]{rll}
2 \cdot |\overline{A B}| + |\overline{BC}|&=& 2 \cdot 35,61 + 31,11& \\[5pt]
&=& 102,31 \; [\text{m}] & \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/bcc9bfda575cccd73b868afa6c9a20df1c6f75c65fc6105dfd8ddb17045b62a3_light.svg)
c)
Die Seitenfläche des Quaders, die 
und enthält, wird als Grundfläche und deren Flächeninhalt mit 
bezeichnet. Die Länge der zugehörigen Höhe des Quaders wird mit bezeichnet.
Folglich hat der pyramidenförmigen Teilkörper eine Grundfläche von 
und eine Höhe von . Somit hat er folgendes Volumen: 
.
Der andere Teilkörper hat ein Volumen von 
. Damit beträgt das gesuchte Verhältnis 
und enthält, wird als Grundfläche und deren Flächeninhalt mit bezeichnet. Die Länge der zugehörigen Höhe des Quaders wird mit bezeichnet.
Folglich hat der pyramidenförmigen Teilkörper eine Grundfläche von und eine Höhe von . Somit hat er folgendes Volumen: .
Der andere Teilkörper hat ein Volumen von . Damit beträgt das gesuchte Verhältnis
d)
Für Abbildung 1 muss der Betrachter parallel zur 
-Achse auf das Saarpolygon blicken. Somit ist 
ein möglicher Vektor.
Für Abbildung 2 muss der Betrachter parallel zur Strecke stehen. Somit ist 
ein möglicher Vektor.
Betrachtung von oben:
-Achse auf das Saarpolygon blicken. Somit ist ein möglicher Vektor.
Für Abbildung 2 muss der Betrachter parallel zur Strecke stehen. Somit ist ein möglicher Vektor.
Betrachtung von oben:
e)
Nach 
gibt 
genau die Ortsvektoren für alle Punkte auf der Strecke 
an. Somit ist 
ein Punkt auf 
Nach 
gilt 
. Folglich steht 
senkrecht zu 
. Da in liegt, gibt 
den Abstand von 
zu 
an.
Dieser Abstand muss nach Aufgabenstellung mit dem Abstand von zu 
übereinstimmen. Der Abstand beträgt 
und stimmt somit mit dem in 
angegebenen Abstand überein.
gibt genau die Ortsvektoren für alle Punkte auf der Strecke an. Somit ist ein Punkt auf
Nach gilt . Folglich steht senkrecht zu . Da in liegt, gibt den Abstand von zu an.
Dieser Abstand muss nach Aufgabenstellung mit dem Abstand von zu übereinstimmen. Der Abstand beträgt und stimmt somit mit dem in angegebenen Abstand überein.