Wahlpflichtteil

Gegeben ist die in $\mathbb{R}$ definierte ganzrationale Funktion $h$ mit $h(x)=4 x^3-6 x.$

(1)

Bestimme eine Gleichung der Stammfunktion $H$ von $h,$ deren Graph durch den Punkt $(1\mid0)$ verläuft.

(2)

Begründe, ohne zu rechnen, dass $\displaystyle\int^3_{-3} h(x) \;\mathrm{d} x=0$ ist.

(3+2 Punkte)

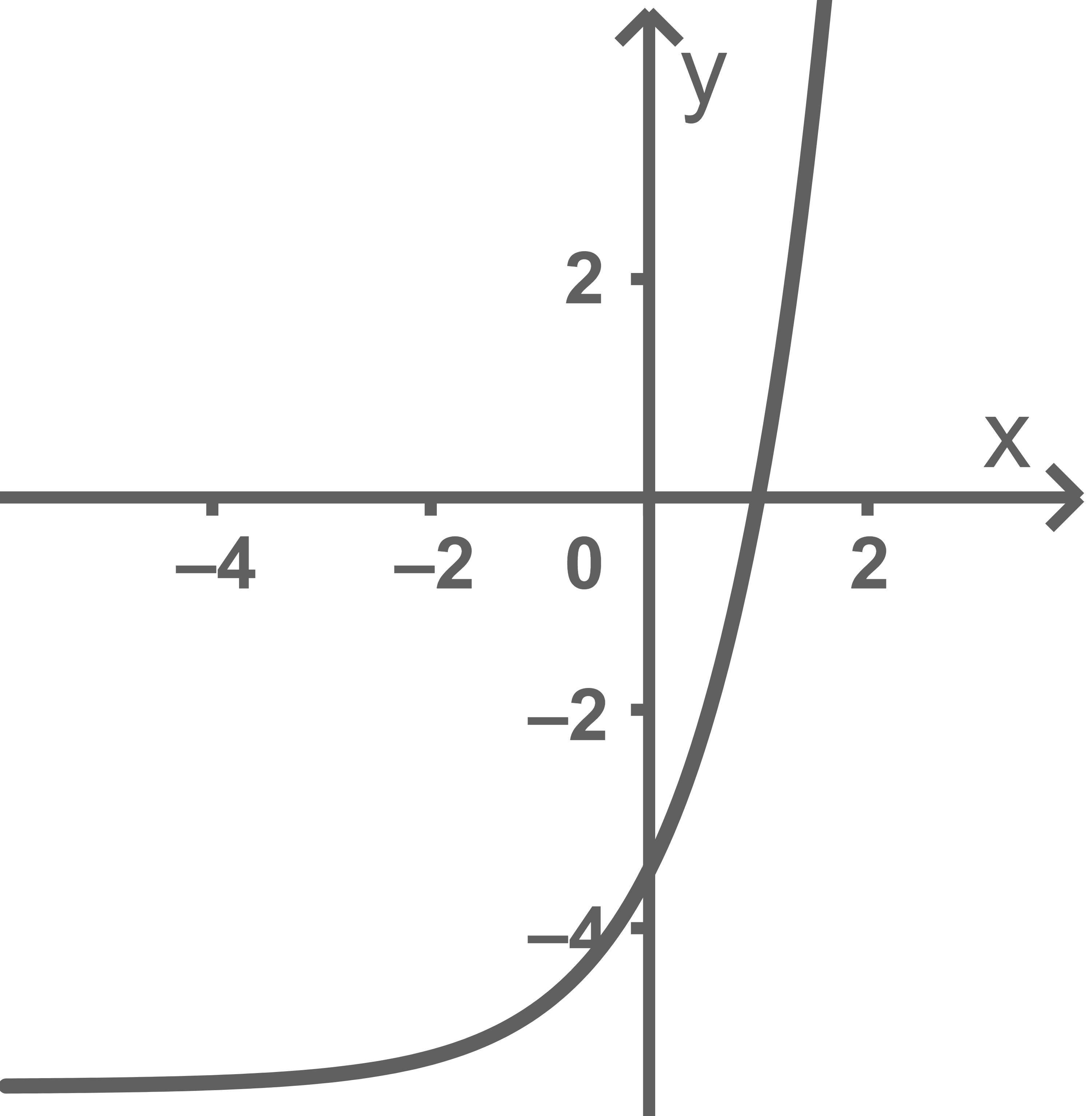
Abbildung 1 zeigt den Graphen der in $\mathbb{R}$ definierten Funktion $g$ mit $g (x)=2 \text{e}^x - 2 \text{e}.$

(1)

Weise nach, dass $1$ eine Nullstelle von $g$ ist.

(2)

Der Graph von $g$ schließt mit den Koordinatenachsen eine Fläche ein.

Berechne ihren Inhalt.

Abbildung 1

(1+4 Punkte)

Betrachtet werden die Punkte $P(3\mid1\mid-1)$ und $Q(4\mid2\mid-4).$

(1)

Begründe, dass die Punkte $P$ und $Q$ auf derselben Seite bezüglich der $xy$ -Ebene liegen.

(2)

Die Punkte $P, Q$ und der Koordinatenursprung $O$ sind die Eckpunkte eines gleichschenkligen Dreiecks, dessen Basis $\overline{O Q}$ die Länge $6 \;\text{LE}$ hat.

Ermittle den Flächeninhalt des Dreiecks.

(1+4 Punkte)

Die Ebene $E$ wird durch die Gleichung $\overrightarrow{x}=\pmatrix{1\\-3\\0}+r \cdot\pmatrix{-3\\4\\1}+s \cdot\pmatrix{3\\-4\\0}$ mit $r, s \in \mathbb{R}$ beschrieben.

(1)

Zeige, dass der Vektor $\pmatrix{4\\3\\0}$ senkrecht zur Ebene $E$ steht.

(2)

Bestimme die Koordinaten eines Punkts $P$ mit folgender Eigenschaft:

Wird der Punkt $P$ an der Ebene $E$ gespiegelt, so hat der entstehende Punkt vom Punkt $P$ den Abstand $20\;\text{LE}.$

(2+3 Punkte)

Abbildung 2 zeigt die Wahrscheinlichkeitsverteilung einer binomialverteilten Zufallsgröße $X$ mit den Parametern $n$ und $p=0,5.$

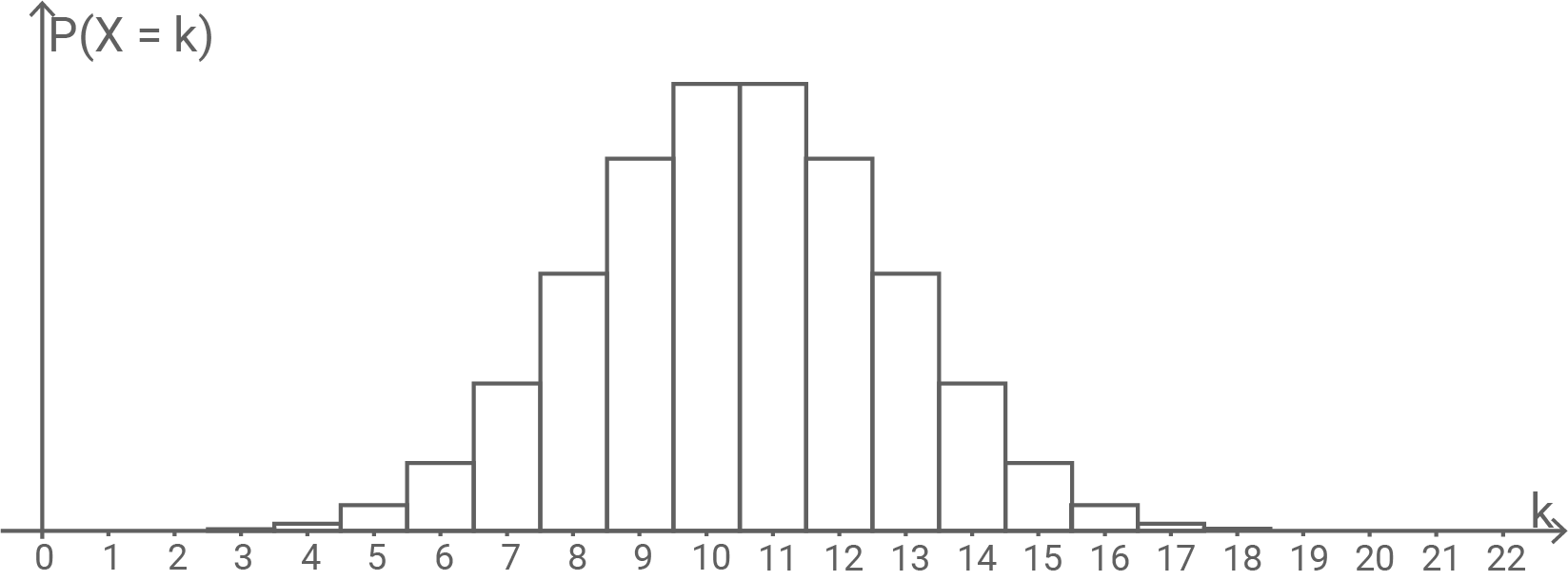
Abbildung 2

(1)

Es gilt $P(X=10)=P(X=11).$

Begründe, dass $n$ nicht gerade ist.

(2)

Es gilt $P(X \geq 9) \approx 0,81$ und $P(X=12) \approx 0,14.$

Berechne unter Verwendung dieser Werte näherungsweise die Wahrscheinlichkeit $P(X=10).$

(2+3 Punkte)

In einer Urne befinden sich $40$ blaue Kugeln.

(1)

Die $40$ blauen Kugeln in der Urne werden durch rote Kugeln ergänzt. Die Wahrscheinlichkeit, beim zufälligen Ziehen einer Kugel eine blaue Kugel zu erhalten, beträgt nun $80 \,\%.$

Bestimme, wie viele rote Kugeln ergänzt wurden.

(2)

In einer anderen Urne befinden sich $40$ blaue und $20$ rote Kugeln.

(i)

Berechne die Wahrscheinlichkeit, dass bei einer Ziehung von drei Kugeln mit Zurücklegen genau zwei blaue Kugeln gezogen werden.

(ii)

Die Zufallsgröße $X$ beschreibt, wie viele blaue Kugeln bei der Ziehung von drei Kugeln mit Zurücklegen gezogen werden.

Die Zufallsgröße $Y$ beschreibt, wie viele blaue Kugeln bei der Ziehung von $n$ Kugeln mit Zurücklegen gezogen werden.

Die Standardabweichung von $Y$ ist doppelt so groß wie die Standardabweichung von $X.$

Gib $n$ an.

(2+3 Punkte)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

(1)

Stammfunktion von $\boldsymbol{h(x)}$ aufstellen

$H(x)=x^4-3 x^2+c ; c \in \mathbb{R}$

$\boldsymbol{c}$ berechnen

$\begin{array}[t]{rlll} H(1) &=& 0 \\[5pt] 1^4-3 \cdot 1^2 +c &=& 0 \mid\; +2 \\[5pt] c &=& 2 \end{array}$

Die Stammfunktion, deren Graph durch den Punkt $(1 \mid 0)$ verläuft, ist:

$H(x)=x^4-3 x^2+2$

(2)

Das Intervall $[-3 ; 3]$ ist symmetrisch zu $0$ und der Graph von $h$ ist punktsymmetrisch zum Koordinatenursprung, da der Term von $h$ nur Potenzen von $x$ mit ungeraden Exponenten enthält.

(1)

$\begin{array}[t]{rll} g(1) &=& 2 \mathrm{e}^1 -2\mathrm{e} \\[5pt] &=& 0 \end{array}$

(2)

$\boldsymbol{G(x)}$ aufstellen

$G(x) = 2\mathrm{e}^x-2\mathrm{e}x$

Integral berechnen

$\begin{array}[t]{rll} \displaystyle\int_{0}^{1}g(x)\;\mathrm{d} x &=& \left[ 2\text{e}^x-2\text{e}x \right]_0^1 \\[5pt] &=& 2\mathrm{e}-2\text{e}-2 \\[5pt] &=& -2 \end{array}$

Somit beträgt der Flächeninhalt $2.$

(1)

Die $z$ -Koordinaten beider Punkte haben das gleiche Vorzeichen.
Somit liegen die Punkte $P$ und $Q$ auf derselben Seite bezüglich der $xy$ -Ebene.

(2)

Mittelpunkt der Basis $\boldsymbol{\overline{O Q}}$ berechnen

$\begin{array}[t]{rlll} \overrightarrow{OM} &=& \dfrac{1}{2} \cdot (\overrightarrow{O} + \overrightarrow{OQ}) \\[5pt] &=&\dfrac{1}{2} \cdot\left(\pmatrix{0\\0\\0} + \pmatrix{4\\2\\-4}\right) \\[5pt] &=& \pmatrix{2\\1\\-2} \end{array}$

Verbindungsvektor vom Mittelpunkt $\boldsymbol{M}$ zum Punkt $\boldsymbol{P}$ bestimmen

$\begin{array}[t]{rlll} \overrightarrow{M P} &=& \overrightarrow{OP}-\overrightarrow{OM} \\[5pt] &=& \pmatrix{3\\1\\-1} - \pmatrix{2\\1\\-2} \\[5pt] &=& \pmatrix{1\\0\\1} \end{array}$

Länge von $\boldsymbol{\overrightarrow{M P}}$ berechnen

$\begin{array}[t]{rlll} \left| \overrightarrow{M P} \right| &=& \sqrt{1^2+0^2+1^2} \\[5pt] &=& \sqrt{2} \end{array}$

Flächeninhalt berechnen

$\begin{array}[t]{rlll} A &=& \dfrac{1}{2} \cdot\left| \overline{OQ} \right| \cdot\left| \overline{MP} \right| \\[5pt] &=&\dfrac{1}{2} \cdot 6 \cdot \sqrt{2} \\[5pt] &=& 3\sqrt{2} \end{array}$

(1)

Ein Vektor $\overrightarrow{n}$ steht genau dann senkrecht zur Ebene $E,$ wenn er senkrecht zu beiden Spannvektoren der Ebene ist.
Um das zu überprüfen, wird jeweils das Skalarprodukt berechnet.

Skalarprodukt mit $\boldsymbol{\overrightarrow{v}_1}$ berechnen

$\begin{array}[t]{rlll} \overrightarrow{v}_1 \cdot \overrightarrow{n} &=& \pmatrix{-3\\4\\1} \cdot \pmatrix{4\\3\\0} \\[5pt] &=& (-3) \cdot 4+4 \cdot 3+1 \cdot 0 \\[5pt] &=& 0 \end{array}$

Skalarprodukt mit $\boldsymbol{\overrightarrow{v}_2}$ berechnen

$\begin{array}[t]{rlll} \overrightarrow{v}_2 \cdot \overrightarrow{n} &=& \pmatrix{3\\-4\\0} \cdot \pmatrix{4\\3\\0} \\[5pt] &=& 3 \cdot 4+(-4) \cdot 3+0 \cdot 0 \\[5pt] &=& 0 \end{array}$

Da beide Skalarprodukte Null sind, steht der Vektor $\overrightarrow{n}$ senkrecht zur Ebene $E.$

(2)

Gegeben ist der Normalenvektor $\overrightarrow{n}= \pmatrix{4\\3\\0}.$

Länge des Vektors $\boldsymbol{\overrightarrow{n}}$ berechnen

$\left| \overrightarrow{n} \right|=\sqrt{4^2+3^2}=\sqrt{25}=5$

Der Einheitsvektor von $\overrightarrow{n}$ ist also $\frac{1}{5}\cdot\pmatrix{4\\3\\0}$

$\(P$ ist der gespiegelte Punkt von $P$ an der Ebene $E.$
Insgesamt sollen $P$ und $\(P$ einen Abstand von $20$ haben. Somit müssen die Punkte einen Abstand von $10$ zur Ebene $E$ haben.

$10 \cdot \dfrac{1}{5} \cdot \pmatrix{4\\3\\0}=\pmatrix{8\\6\\0}$

Ein möglicher Spiegelpunkt auf der Ebene ist der Stützvektor der Ebene $E.$

Koordinaten eines Punktes $\boldsymbol{P}$ berechnen

$\pmatrix{1\\-3\\0}+\pmatrix{8\\6\\0}=\pmatrix{9\\3\\0}$

(1)

Da die Wahrscheinlichkeiten bei $k=10$ und $k=11$ gleich groß und am größten sind, liegt der Erwartungswert $E(X)=n \cdot 0,5$ genau dazwischen - also zwischen zwei ganzen Zahlen. Das geht nur, wenn $n$ ungerade ist.

(2)

Gegeben ist $P(X \geq 9) \approx 0,81$ und $P(X=12) \approx 0,14.$ Wegen der Symmetrie gilt dann auch $P(X=9) \approx 0,14.$
Außerdem ist $P(X \geq 11)=0,5,$ also folgt:

$P(X=10) \approx 0,81-0,14-0,5=0,17$

(1)

Die gesamte Anzahl an Kugeln $n$ in der Urne setzt sich zusammen durch die $40$ blauen Kugeln und eine unbekannte Anzahl $r$ an roten Kugeln:

$n=40+r$

Die Wahrscheinlichkeit, eine blaue Kugel zu ziehen, soll $80 \, \%$ betragen:

$\begin{array}[t]{rlll} 0,8 \cdot n &=& 40 \\[5pt] 0,8 \cdot (40+r) &=& 40 &\mid\; : 0,8 \\[5pt] 40+r &=& \dfrac{40}{0,8} &\mid\; -40 \\[5pt] r &=& 50-40 \\[5pt] r &=& 10 \end{array}$

Es wurden $10$ rote Kugeln hinzugefügt.

(2)

(i)

Da mit Zurücklegen gezogen wird und jede Kugel die gleiche Wahrscheinlichkeit behält, liegt eine Binomialverteilung mit den Parametern $n=3$ und $p=\frac{40}{60}=\frac{2}{3}$ vor.

$\boldsymbol{P(X=2)}$ berechnen

$\begin{array}[t]{rlll} P(X=2) &=& \displaystyle\binom{3}{2} \cdot\left(\dfrac{2}{3}\right)^2 \cdot\left(\dfrac{1}{3}\right)^1 \\[5pt] &=& 3 \cdot \dfrac{4}{9}\cdot\dfrac{1}{3} \\[5pt] &=& 3 \cdot \dfrac{4}{27} \\[5pt] &=& \dfrac{12}{27} \\[5pt] &=& \dfrac{4}{9} \end{array}$

(ii)

Standardabweichung $\boldsymbol{\sigma_X}$ berechnen

$\begin{array}[t]{rlll} \sigma_X &=& \sqrt{3 \cdot \dfrac{2}{3} \cdot \dfrac{1}{3}} \\[5pt] &=& \sqrt{\dfrac{2}{3}} \end{array}$

Standardabweichung $\boldsymbol{\sigma_Y}$ berechnen

$\begin{array}[t]{rlll} \sigma_Y &=& \sqrt{n \cdot \dfrac{2}{3} \cdot \dfrac{1}{3}} \\[5pt] &=& \sqrt{\dfrac{2n}{9}} \end{array}$

Bedingung $\boldsymbol{2\sigma_X=\sigma_Y}$ aufstellen

$\begin{array}[t]{rlll} 2\sigma_X &=& \sigma_Y \\[5pt] 2 \cdot \sqrt{\dfrac{2}{3}} &=& \sqrt{\dfrac{2n}{9}} &\mid\; ^2 \\[5pt] \dfrac{8}{3} &=& \dfrac{2n}{9} &\mid\; \cdot 9 \\[5pt] 24 &=& 2n &\mid\; :2 \\[5pt] 12 &=& n \end{array}$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?