Vektorielle Geometrie
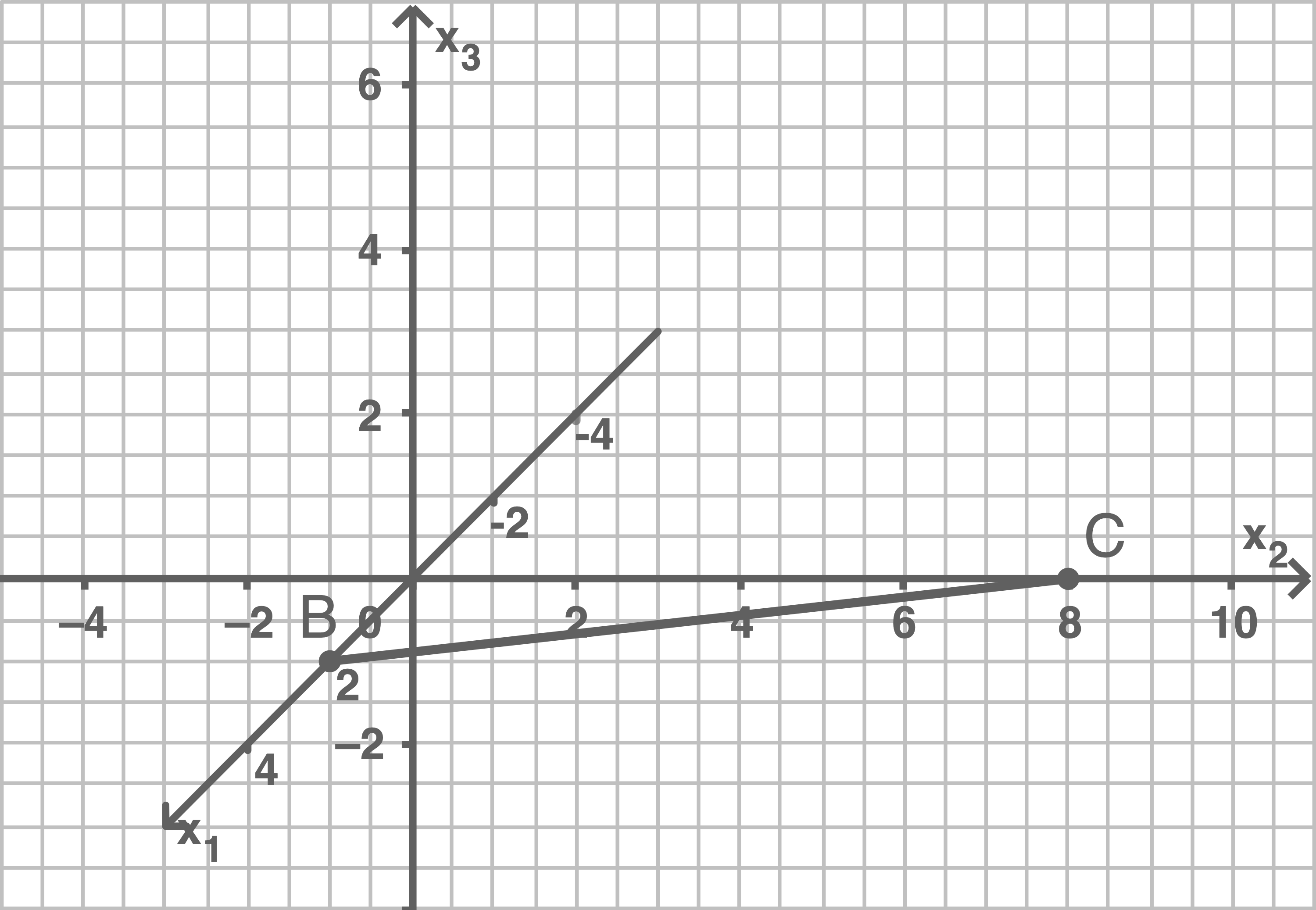
Betrachtet wird ein gerades Prisma mit den Eckpunkten und
Grundfläche ist das Dreieck
Abbildung 1 zeigt die Kante des Prismas.
Zeichne das Prisma in Abbildung 1 ein und berechne das Volumen des Prismas.
Das Dreieck liegt in der Ebene
Gib eine Gleichung von in Parameterform an.
Berechne die Größe des Innenwinkels des Dreiecks am Eckpunkt
Begründe, dass das Dreieck parallel zur
-Ebene liegt.
Im Folgenden wird die Gerade mit der Gleichung
betrachtet.
Des Weiteren wird der Punkt durch einen Punkt
mit
ersetzt. Für jeden Wert von
liegt der Punkt
auf der Gerade
(vgl. Abbildung 2).
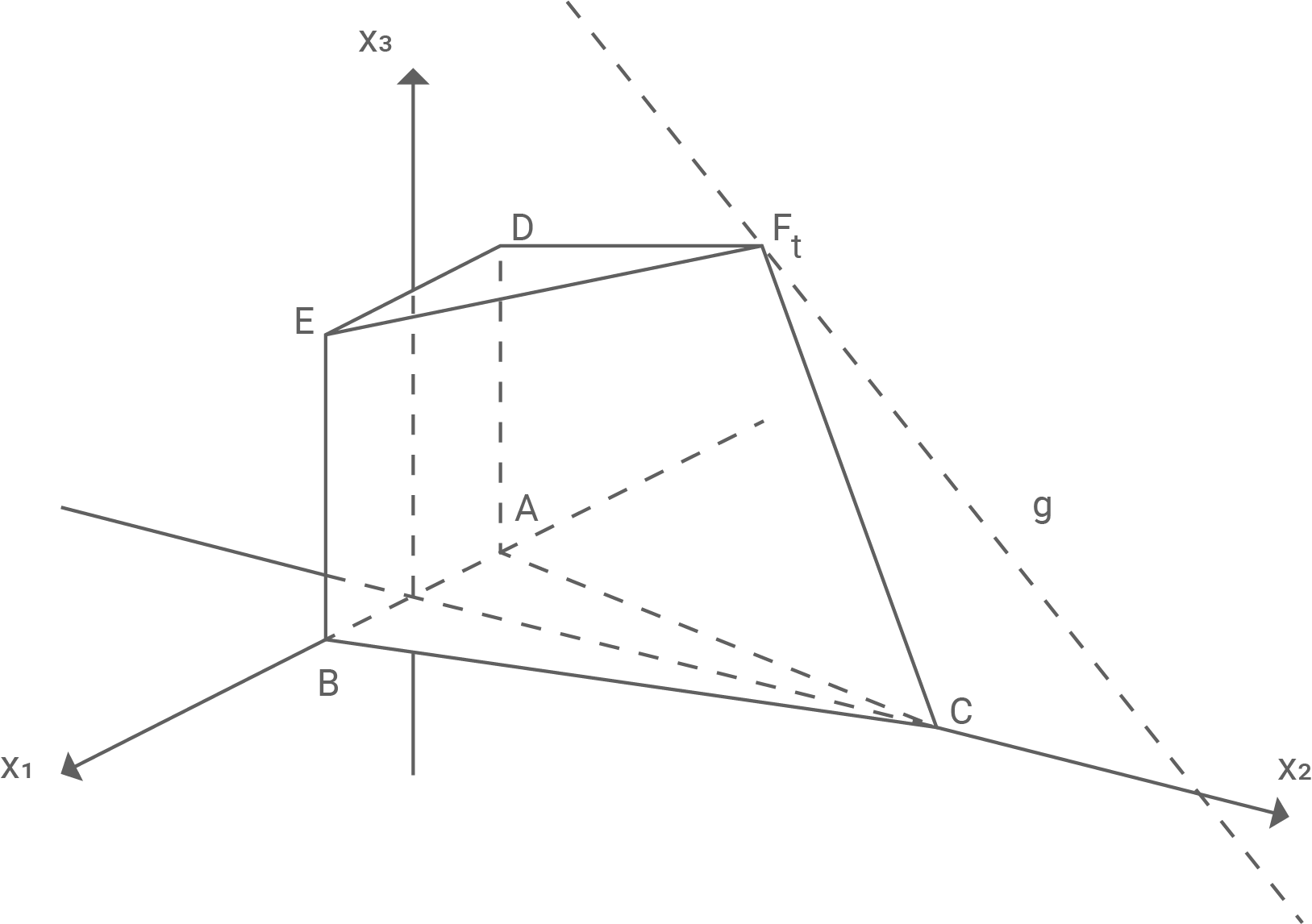
Mit wird der Mittelpunkt der Basis
des gleichschenkligen Dreiecks
bezeichnet.
Zeige rechnerisch, dass für die Strecke
senkrecht auf der Gerade
steht.
Begründe ohne Rechnung, dass der Flächeninhalt des Dreiecks für
am kleinsten ist.
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?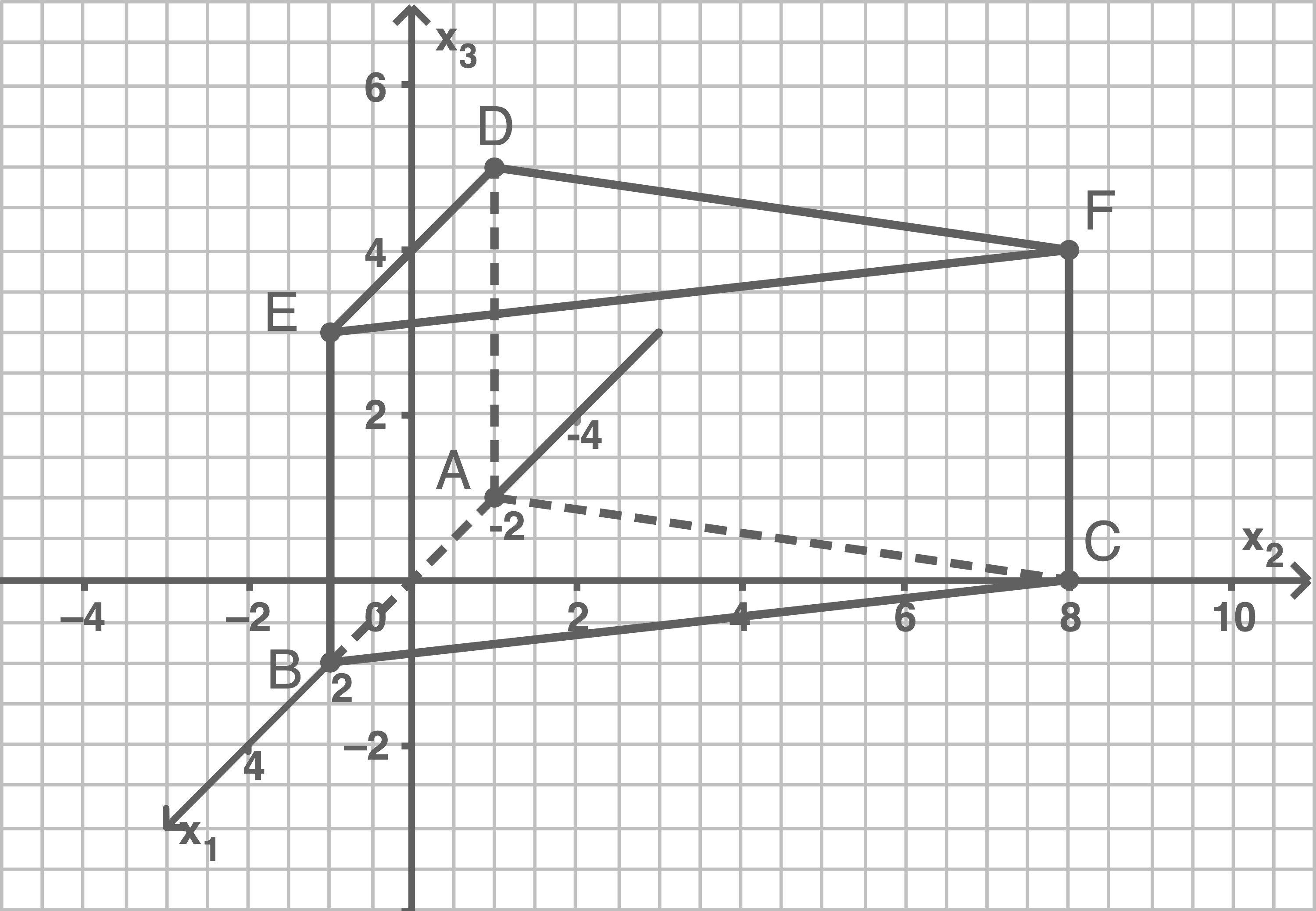
Volumen:
Vektor berechnen
Vektor berechnen
Parametergleichung der Ebene aufstellen
Mit dem CAS folgt:
Da die beiden Vektoren und
jeweils die dritte Koordinate
besitzen, verlaufen sie parallel zur
-Ebene. Deshalb ist auch das Dreieck, das durch diese Vektoren aufgespannt wird, parallel zur
-Ebene.
Punkt berechnen
Mittelpunkt der Strecke
berechnen
Vektor berechnen
Skalarprodukt mit Richtungsvektor der Geraden berechnen
Somit ist gezeigt, dass die Strecke senkrecht auf der Geraden
steht.
Für jedes ist
die Basis und
die Höhe des gleichschenkligen Dreiecks
Da für
senkrecht auf
steht, besitzt das Dreieck
für diesen Wert von
die kleinste Höhe und somit den kleinsten Flächeninhalt.