Analysis 1

Gegeben ist die in $\mathbb{R}$ definierte Funktion $f$ mit $f(x)=\dfrac{1}{100} \cdot(x-6) \cdot e^{-0,17 x+6}.$

Gib die Koordinaten des Schnittpunkts des Graphen von $f$ mit der $y$ -Achse sowie das Verhalten von $f$ für $x \rightarrow-\infty$ und $x \rightarrow+\infty$ an.

(3 BE)

Im Folgenden wird die Lösung zu einer Aufgabenstellung in Bezug auf den Graphen von $f$ dargestellt:

$f^{\prime \prime}(x)=0 \Leftrightarrow x=\dfrac{302}{17}.$

$f^{\prime \prime \prime}\left(\dfrac{302}{17}\right) \neq 0.$

$f^{\prime}\left(\dfrac{302}{17}\right) \lt 0.$

Gib die sich daraus ergebenden Eigenschaften des Graphen von $f$ im Punkt $\left(\dfrac{302}{17}\mid f\left(\dfrac{302}{17}\right)\right)$ an.

(3 BE)

Der Graph von $f$ schließt mit den beiden Koordinatenachsen eine Fläche ein. Die Fläche soll durch eine Gerade, die parallel zur $y$ -Achse verläuft, in zwei gleich große Teilflächen zerlegt werden.

Bestimme eine Gleichung dieser Gerade.

(4 BE)

Ein Mobilfunkanbieter betreibt eine Hotline, die an jedem Tag $24$ Stunden erreichbar ist.
Die Wartezeit eines Anrufers dieser Hotline ist abhängig vom Zeitpunkt des Anrufs. Durch die in $\mathbb{R}$ definierte Funktion $w$ mit

$w(x)=100 \cdot f(x)=(x-6) \cdot e^{-0,17 x+6}$

kann die Wartezeit an einem bestimmten Tag für die Zeitpunkte von $8: 00$ Uhr bis einschließlich $22: 00$ Uhr beschrieben werden.

Dabei bezeichnet $x$ den Zeitpunkt des Anrufs in Stunden nach $0:00$ Uhr und $w(x)$ die Wartezeit in Sekunden. Nimmt $w$ beispielsweise an der Stelle $10,25$ den Wert von etwa $300$ an, so beträgt die Wartezeit für einen Anruf um $10: 15$ Uhr etwa $300$ Sekunden.

(1)

Berechne die Wartezeit für einen Anruf um $9:00$ Uhr.

(2)

Ein anderer Anruf erfolgt später als $9:00$ Uhr und hat eine Wartezeit von $200$ Sekunden.

Bestimme die Uhrzeit dieses Anrufs auf eine Minute genau.

(4 Punkte)

Ermittle rechnerisch für den Zeitraum von $8: 00$ Uhr bis einschließlich $22: 00$ Uhr den Zeitpunkt eines Anrufs, zu dem die Wartezeit am längsten ist, und den Zeitpunkt eines Anrufs, zu dem die Wartezeit am kürzesten ist.

(6 Punkte)

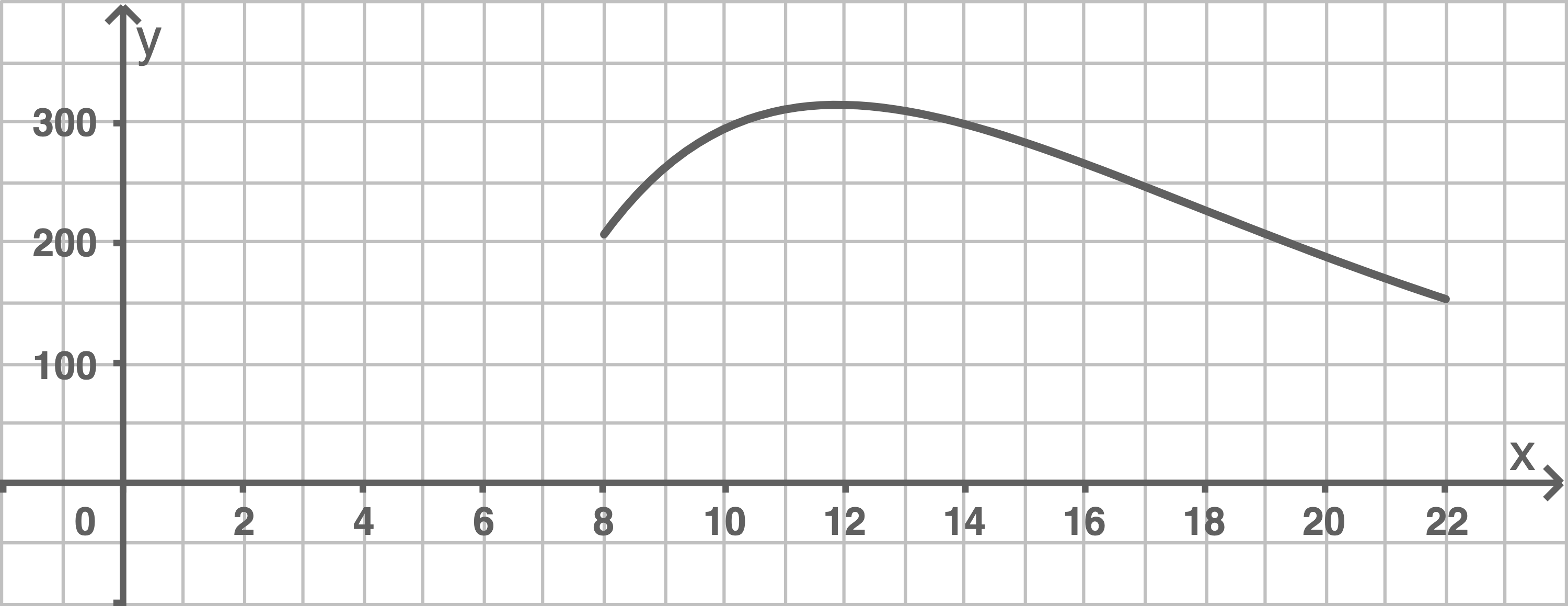
Die Abbildung zeigt den Graphen von $w$ für $8 \leq x \leq 22.$

Für reelle Zahlen $a$ und $b$ mit $8 \leq a \lt b \leq 22$ gilt:

Wenn $\displaystyle\int_{a}^{b}(250-w(x))\;\mathrm{d}x=0$ ist, so beträgt die durchschnittliche Wartezeit für Anrufe zwischen den durch $a$ und $b$ gegebenen Zeitpunkten $250$ Sekunden.

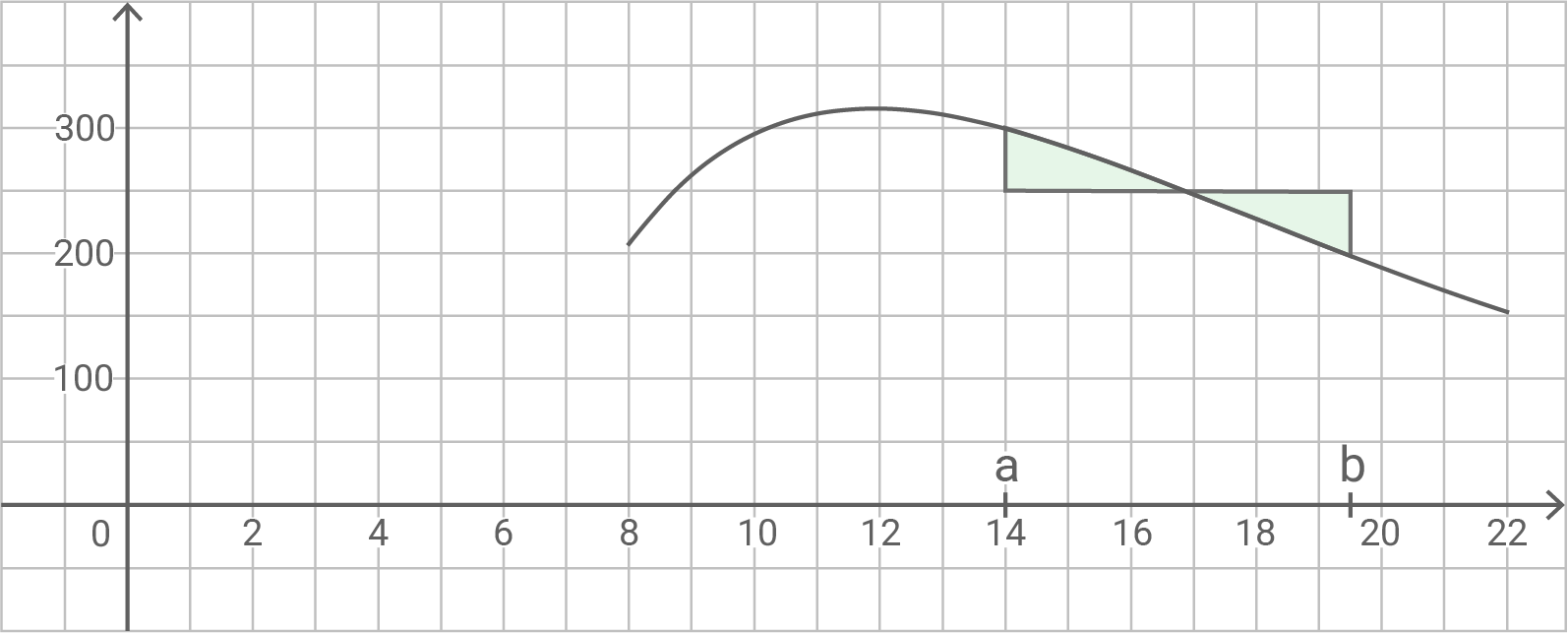
Bestimme durch geeignete Eintragungen in der Abbildung jeweils einen möglichen Wert für $a$ und $b$ , sodass zwischen den zugehörigen Zeitpunkten die durchschnittliche Wartezeit $250$ Sekunden beträgt.

Beschreibe dein Vorgehen.

Graf mit x- und y-Achse, zeigt eine Kurve mit ansteigendem und fallendem Verlauf.

Abbildung

(5 Punkte)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Koordinaten des Schnittpunktes mit der $\boldsymbol{y}$ -Achse bestimmen

Mit der graphischen Darstellung des CAS folgt:

$\left(0 \left\lvert\,-\frac{3}{50} \text{e}^6\right.\right)$

Verhalten gegen Unendlich bestimmen

$\begin{array}[t]{rlll} \lim\limits_{x\to+\infty}f(x) &=& 0 \\[5pt] \lim\limits_{x\to-\infty}f(x) &=& -\infty \end{array}$

Der Graph von $f$ hat im Punkt $\left(\frac{302}{17} \left\lvert\, f\left(\frac{302}{17}\right)\right.\right)$ wegen der notwendigen Bedingung $\(f$ und wegen der hinreichenden Bedingung $\(f$ einen Wendepunkt und wegen $\(f$ eine negative Steigung.

Da $f$ bei $x=6$ eine Nullstelle hat, liegt die betrachtete Fläche im Intervall $0 \leq a \leq 6.$

Gesucht ist eine Gerade parallel zur $y$ -Achse, die diese Fläche in zwei gleich große Teilflächen teilt. Das bedeutet: Gesucht ist ein Wert $a \in[0 ; 6]$ , für den gilt:

$\displaystyle\int_0^6 f(x) \;\mathrm{d} x=2 \cdot \displaystyle\int_0^a f(x) \;\mathrm{d} x$

Auflösen mit dem CAS nach $a$ liefert die Lösung $a_1 \approx 1,39.$ Damit ist $x=1,39$ eine Gleichung der Gerade.

(1)

Wartezeit um $\boldsymbol{9:00}$ Uhr berechnen

$w(9) \approx 262$

Die Wartezeit beträgt etwa $262$ Sekunden.

(2)

Uhrzeit des Anrufs bestimmen

$\begin{array}[t]{rlll} w(x) &=& 200 \\[5pt] (x-6) \cdot \text{e}^{-0,17 x+6} &=& 200 \end{array}$

Mit dem CAS folgt für $x \approx 19,39.$

$0,39 \cdot 60 \approx 23$

Der gesuchte Zeitpunkt ist etwa $19: 23$ Uhr

Die längste Wartezeit ist beim lokalen Maximum der Funktion $w.$
Die kürzeste Wartezeit ist entweder um $8:00$ Uhr oder um $22:00$ Uhr.

Ableiten von $w(x)$ mit dem CAS liefert:

$w^{\prime}(x)=\mathrm{e}^{-0,17 x+6} \cdot(2,02-0,17 x)$

Nullsetzen der Ableitung mithilfe des CAS liefert als Maximum des Graphen:

$x=\dfrac{202}{17} \approx 11,88$

Einsetzen von $x$ in $w(x)$ liefert für den Funktionswert:

$w\left(\dfrac{202}{17}\right) \approx 314,81$

Durch systematisches Ausprobieren folgt für das Minimum des Graphen:

$\begin{array}[t]{rlll} w(8) &\approx& 207,09 \\[5pt] w(22) &\approx& 153,33 \\[5pt] \end{array}$

Uhrzeit zum Zeitpunkt der längsten Wartezeit berechnen

$0,88\cdot 60\approx53$

Somit ist die längste Wartezeit um etwa $11:53$ Uhr und die kürzeste Wartezeit um $22:00$ Uhr.

Mögliche Werte für $\boldsymbol{a}$ und $\boldsymbol{b}$ bestimmen

Durch geeignete Eintragungen folgt für die Werte $a \approx 14$ und $b \approx 19,5.$

Vorgehen beschreiben

Als erstes wird der Ausschnitt der Gerade $g: y=250$ eingezeichnet. Dann werden auf der $x$ -Achse die Stellen $a$ und $b$ markiert, sodass die Fläche zwischen dem Graphen von $w,$ der Gerade $g$ sowie den Geraden mit den Gleichungen $x=a$ und $x=b$ aus zwei Flächenstücken gleichen Inhalts besteht.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?