Aufgabe 4

Aufgabenstellung

Im Folgenden betrachten wir die Entwicklung von Wolfspopulationen. Dabei beschränken wir uns ausschließlich auf die weiblichen Mitglieder einer Population, die aus Welpen ( $w$ ), jungen Fähen ( $j$ ) sowie ausgewachsenen Fähen ( $a$ ) bestehen soll. Alle Fähen sind vermehrungsfähig. Die Welpen entwickeln sich ein Jahr nach der Geburt zu jungen Fähen und ein Jahr später zu ausgewachsenen Fähen.

Die folgende Tabelle zeigt die Verteilung einer in der Wildnis lebenden Population für die Jahre 2013 und 2014:

	2013	2014
$w$	65	52
$j$	8	26
$a$	20	16

Tabelle

Modellhaft lässt sich die Entwicklung mit der Matrix $A$ beschreiben:

		von:	$w$	$j$	$a$
	$w$		$\begin{pmatrix}0&1,5&2\\[2pt]b&0&0\\[2pt]0&0,5&0,6\end{pmatrix}$
nach:	$j$	$A=$
	$a$

a) (1) Begründe mit den Daten aus der Tabelle, dass $b=0,4$ gilt.

(3P)

(2) Interpretiere die weiteren von Null verschiedenen Einträge in der Matrix $A$ im Sachzusammenhang.

(4P)

b) (1) Berechne die Verteilungen, die nach diesem Modell in den Jahren 2015 und 2016 zu erwarten sind.

(4P)

(2) Bestimme die Verteilung, die nach diesem Modell im Jahr 2012 vorgelegen hätte.

(5P)

(3) Zeige, dass sich in diesem Modell die Population aus 2011 nicht bestimmen lässt.

(3P)

(4) Ein Biologe behauptet, dass weniger als $15\,$ % aller Welpen mindestens ein Alter von drei Jahren erreichen.

Prüfe, ob nach der obigen Modellierung mit der Matrix $A$ die Behauptung des Biologen zutrifft.

(4P)

c) Wölfe, die in einem Tierpark leben, haben andere Überlebens- und Fortpflanzungsraten. Für einen Tierpark kann die Entwicklung seiner Wolfspopulation durch die folgende Matrix $B$ modelliert werden:

$B=\begin{pmatrix}0&1&d\\0,8&0&0\\0&0,75&0,7\end{pmatrix}$

(1) Beschreibe im Sachzusammenhang die Einträge in der zweiten Spalte der Matrix $B$ im Vergleich zu den Einträgen in der zweiten Spalte der Matrix $A$ .

(2P)

(2) Wegen der räumlichen Beschränkung will die Tierparkleitung die Gesamtzahl der Wölfe konstant halten. Das soll durch eine strikte Geburtenkontrolle gewährleistet werden.

Zeige, dass nur für den Wert $d=0,1$ eine von $\begin{pmatrix}0\\0\\0\end{pmatrix}$ verschiedene stationäre Verteilung existiert, d. h. eine Verteilung, die sich innerhalb eines Jahres nicht ändert.

(7P)

(3) Ermittle für den Wert $d=0,1$ die kleinstmögliche Gesamtpopulation mit stationärer Verteilung

$\vec{n}=\begin{pmatrix}n_1\\n_2\\n_3\end{pmatrix}\neq \begin{pmatrix}0\\0\\0\end{pmatrix}$ mit natürlichen Zahlen $n_1, n_2$ und $n_3$ .

(4P)

d) Für die Population in dem obigen Tierpark wird eine neue Modellierung gewählt: Die Entwicklungsstufe der Welpen wird mit der Überlebensrate von $80\,$ % beibehalten, die Entwicklungsstufen der jungen Fähen und ausgewachsenen Fähen werden zu einer Stufe zusammengefasst. Die neue Modellierung soll durch die Matrix

$C=\begin{pmatrix}0&g\\0,8&h\end{pmatrix}$

mit $g\gt 0$ und $0\leq h \lt 1$ dargestellt werden. Die Population der Welpen und Fähen soll mit insgesamt 19 Tieren konstant bleiben.

(1) Zeige, dass in dem neuen Modell eine stationäre Verteilung mit 11 Welpen nicht vorkommen kann.

(7P)

(2) Zeige, dass sich für $g=\frac{5}{14}$ und $h=\frac{5}{7}$ eine stationäre Verteilung mit 5 Welpen und 14 Fähen ergibt.

(2P)

(3) Mit den Werten aus (2) ist $C=\begin{pmatrix}0&\frac{5}{14}\\0,8&\frac{5}{7}\end{pmatrix}$ . Ein Taschenrechner liefert z. B.

$C^{17}=\begin{pmatrix}0,2222222218&0,2777777779\\0,6222222226&0,7777777777\end{pmatrix}$ .

Die Potenzen $C^n$ der Matrix $C$ streben mit wachsendem $n$ gegen die Matrix

$G=\begin{pmatrix}\frac{2}{9}&\frac{5}{18}\\\frac{28}{45}&\frac{7}{9}\end{pmatrix}$ .

Mit Hilfe der Matrix $G$ lässt sich die langfristige Entwicklung einer Population ermitteln.

Leider fallen in einem Jahr alle fünf Welpen der Population einer Infektionskrankheit zum Opfer. Daraufhin beschließt die Tierparkleitung die Anschaffung von vier zusätzlichen Fähen.

Ermittle die langfristige Entwicklung der neuen Population.

(5P)

a) (1)

$\blacktriangleright$ Wert für $\boldsymbol{b}$ begründen

Du sollst hier anhand der Tabelle begründen, warum für den Eintrag $b$ der Matrix $A$ $b = 0,4$ gilt. Beachte dabei, dass $A$ eine Übergangsmatrix ist. Der Eintrag der $i$ -ten Zeile und $j$ -ten Spalte einer Übergangsmatrix gibt die Übergangsrate von Altersgruppe $j$ in Altersgruppe $i$ an. Überlege also, welche Bedeutung der Parameter $b$ hat und ziehe anschließend Rückschlüsse auf die Tabelle.

Die Variable $b$ steht in der Spalte $w$ und in Zeile $j$ . Sie steht demnach für die Übergangsrate von $w$ nach $j$ , gibt also an, wie viele der Welpen sich nach einem Jahr zu jungen Fähen entwickeln. Da innerhalb dieses Jahres auch alle zuvor vorhandenen jungen Fähen ausgewachsen sind, sind alle jungen Fähen, die im Jahr 2014 vorhanden sind im Jahr 2013 Welpen gewesen. Die Übergangsrate von $w$ nach $j$ ergibt sich also aus dem relativen Anteil der Welpen, die überleben:

$b = \dfrac{j_{2014}}{w_{2013}} = \dfrac{26}{65} = 0,4\qquad$ Grünes Häkchen-Symbol auf transparentem Hintergrund.

(2)

$\blacktriangleright$ Einträge der Matrix interpretieren

In der Matrix $A$ kommen noch 4 weitere von Null verschiedene Elemente vor. Diese sollst du im Sachzusammenhang interpretieren. Nutze dazu, wie oben, die allgemeine Bedeutung der Übergangsmatrix und die Erklärungen zum Sachzusammenhang im Einleitungstext.

Eintrag $\boldsymbol{a_{1,2} = 1,5}$ :

Der Eintrag $a_{1,2} = 1,5$ gibt die Übergangsquote von $j$ nach $w$ an. Da sich ein Wolf natürlich nicht rückwärts entwickeln kann, bedeutet dies im Sachzusammenhang, dass jede junge Fähe im Schnitt $1,5$ Welpen gebährt.

Eintrag $\boldsymbol{a_{3,2} = 0,5}$ :

Der Eintrag $a_{3,2} = 0,5$ gibt die Übergangsrate von $j$ nach $a$ an. Das bedeutet, dass sich die Hälfte aller jungen Fähen im nächsten Jahr zu ausgewachsenen Fähen entwickeln. Da Fähen laut Aufgabenstellung nicht zwei Jahre hintereinander jung sein können, gibt diese Übergangsquote die Überlebensrate der jungen Fähen an. Insgesamt bedeutet dies, dass nach einem Jahr die Hälfte aller jungen Fähen überlebt hat und damit ausgewachsen ist.

Eintrag $\boldsymbol{a_{1,3} = 2}$ :

Analog zum ersten Eintrag in der zweiten Spalte, gibt der erste Eintrag der dritten Spalte die Anzahl der Welpen an, die jede ausgewachsene Fähe im Schnitt pro Jahr bekommt.

Eintrag $\boldsymbol{a_{3,3} = 0,6}$ :

Dieser Eintrag gibt die Übergangsquote von ausgewachsener Fähe zu ausgewachsener Fähe an. Dies entspricht der Überlebensrate der ausgewachsenen Fähen.

b) (1)

$\blacktriangleright$ Verteilung der nächsten Jahre berechnen

Den Verteilungsvektor $\overrightarrow{v}_i$ , der die Verteilung der Population im $i$ -ten Entwicklungsschritt beschreibt, lässt sich allgemein über folgende Formel berechnen:

$\overrightarrow{v}_i = A \cdot \overrightarrow{v}_{i-1} = A^{i}\cdot \overrightarrow{v}_0$

Dabei ist $A$ die betrachtete Übergangsmatrix.

Im vorliegenden Fall findet pro Jahr ein Entwicklungsschritt statt. Das bedeutet, du kannst die gesuchte Verteilung für das Jahr 2015 mit Hilfe der Verteilung für 2014 und die Verteilung für das Jahr 2016 mit der davor berechneten Verteilung für 2015 berechnen. Die Verteilung für 2014 kannst du aus der Tabelle ablesen:

$\overrightarrow{v}_{2014} = \begin{pmatrix}52\\26\\16\end{pmatrix}$

Nun kannst du die Verteilung für das Jahr 2015 und 2016 mit dem CAS berechnen: Berechne das Produkt $A \cdot \overrightarrow{v}_{2014}$ für die Verteilung in 2015 und das Produkt $A \cdot \overrightarrow{v}_{2015}$ für die Verteilung in 2016:

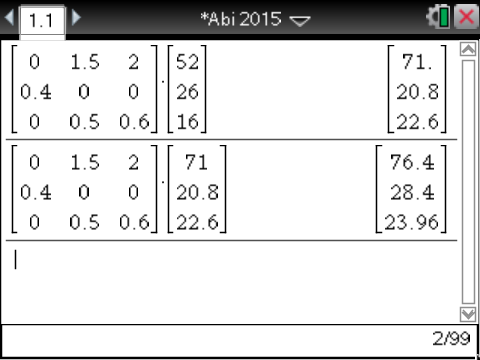Mathematikschnittstelle mit Zahlen und Matrizen, vermutlich für eine Abi-Prüfung.

Es ergibt sich:

$\begin{array}[t]{rll} \vec{v_{2015}}&=&\begin{pmatrix}71\\20,8\\22,6\\\end{pmatrix}\; , \vec{v_{2016}}&=&\begin{pmatrix}76,4\\28,4\\23,96\\\end{pmatrix}\\ \end{array}$

Im Jahr 2015 ist eine Verteilung mit $71$ Welpen, $20,8$ bzw. ca. $21$ jungen Fähen und $22,6$ bzw. ca. $23$ ausgewachsenen Fähen zu erwarten, im Jahr 2016 eine Verteilung mit $76,4$ bzw. ca. $76$ Welpen, $28,4$ bzw. ca. $28$ jungen Fähen und $23,96$ bzw. ca. $24$ ausgewachsenen Fähen.

(2)

$\blacktriangleright$ Verteilung vom Vorjahr berechnen

In dieser Aufgabe sollst du nun eine vorherige Verteilung berechnen, anstatt einer zukünftigen. Dazu kannst du dieselbe Gleichung verwenden. Setze diesmal $\overrightarrow{v}_{2013}$ ein und löse das dabei entstehende lineare Gleichungssystem für $\overrightarrow{v}_{2012}= \begin{pmatrix}v_1\\v_2\\v_3\end{pmatrix}$ . Hast du einen CAS zur Verfügung, so kannst du mit der Matrix $A^{-1}$ arbeiten:

$\overrightarrow{v}_{2012} = A^{-1}\cdot \overrightarrow{v}_{2013}\\$

$\overrightarrow{v}_{2013}$ kannst du aus der Tabelle ablesen: $\overrightarrow{v}_{2013} = \begin{pmatrix}65\\8\\20\end{pmatrix}$ . Gib die Matrix wie oben in deinen CAS ein und berechne dann das Produkt $A^{-1}\cdot \overrightarrow{v}_{2013}$

Matrix-Berechnung auf einem Taschenrechner mit Ergebnissen und Eingabefeld.

Damit gilt nun $\overrightarrow{v}_{2012} = \begin{pmatrix}v_1\\v_2\\v_3\end{pmatrix} = \begin{pmatrix}20\\10\\25\end{pmatrix}$ .

Nach dem Modell hätte im Jahr 2012 eine Verteilung mit $20$ Welpen, $10$ jungen Fähen und $25$ ausgewachsenen Fähen vorgelegen.

(3)

$\blacktriangleright$ Zeigen, dass sich die Population aus 2011 nicht bestimmen lässt

Hier ist es deine Aufgabe zu zeigen, dass sich in diesem Modell die Population aus 2011 nicht bestimmen lässt. Berechne dazu die Verteilung aus dem Jahr 2011, die nach diesem Modell vorliegt. Anhand dieser Verteilung erkennst du, dass damit nicht die Population aus dem Jahr 2011 bestimmt werden kann.

Die Verteilung aus dem Jahr 2012 hast du aus dem vorherigen Aufgabenteil gegeben:

$\overrightarrow{v}_{2012} = \begin{pmatrix}20\\10\\25\end{pmatrix}$

Damit kannst du nun wie im vorherigen Aufgabenteil die Verteilung aus dem vorigen Jahr mit deinem CAS bestimmen:

Mathematische Berechnungen auf einem Bildschirm mit Matrizen und Ergebnissen.

Damit gilt nun $\overrightarrow{v}_{2011} = \begin{pmatrix}v_1\\v_2\\v_3\end{pmatrix} = \begin{pmatrix}25\\380\\-275\end{pmatrix}$ .

Da die dritte Komponente negativ ist und eine Population nur positive Werte besitzt, kann durch das Modell nicht die Population im Jahr 2011 beschrieben werden.

(4)

$\blacktriangleright$ Prozentsatz berechnen

Um die Behauptung des Biologen zu überprüfen, berechne den Prozentsatz der Welpen, die ein Alter von mindestens drei Jahren erreichen mit Hilfe der Pfadmultiplikationsregel.

Im Aufgabenteil a) hast du gesehen, dass der Anteil der Welpen, die ein Alter von $1$ Jahr erreichen, also zu einer jungen Fähe heranwachsen, $a_{2,1}=0,4$ beträgt.
Analog dazu beträgt der Anteil der jungen Fähen, die ein Alter von $2$ Jahren erreichen, also zu ausgewachsenen Fähen heranwachsen, $0,5$ , also $50\,\%$ und der Anteil der ausgewachsenen Fähen, die das nächste Lebensjahr erreichen, beträgt $0,6 = 60\,\%$ .

Mit der Pfadmultiplikationsregel ergibt sich dementsprechend folgender Prozentsatz:

$p = 0,4\cdot 0,5\cdot 0,6 = 0,12 = 12\,\%$ .

Nach dem angegebenen Modell mit der Matrix A erreichen durchschnittlich $12\,\%$ aller Welpen mindestens ein Alter von $3$ Jahren. Die Behauptung des Biologen trifft nach diesem Modell demnach zu.

c) (1)

$\blacktriangleright$ Einträge im Sachzusammenhang vergleichen

Im Aufgabenteil a) hast du bereits die Einträge der Matrix $A$ im Sachzusammenhang beschrieben. Diese Bedeutungen treffen auch auf die Einträge der Matrix $B$ zu, vergleiche also die Überlebens- und Geburtenraten:

Eintrag $\boldsymbol{b_{1,2} = 1}$ :

Der erste Eintrag der zweiten Spalte entspricht der Anzahl der Welpen, die eine junge Fähe durchschnittlich gebährt. In der Matrix $B$ ist dieser Eintrag geringer. Im Tierpark bringt jede junge Fähen also im Schnitt nur einen Welpen zur Welt, während sie in freier Wildbahn $1,5$ gebährt.

Eintrag $\boldsymbol{b_{2,2} = 0}$ :

Dieser Eintrag ist in beiden Matrizen gleich und ist deshalb Null, weil es keine jungen Fähen gibt, die im folgenden Jahr immernoch junge Fähen bleiben. Diese Information kannst du dem Einleitungstext der Aufgabenstellung entnehmen.

Eintrag $\boldsymbol{b_{3,2} = 0,75}$ :

Der dritte Eintrag der zweiten Spalte beschreibt die Überlebensrate der jungen Fähen. Im Schnitt überleben also $0,75 = 75\,\%$ aller jungen Fähen im Tierpark und entwickeln sich zu ausgewachsenen Fähen. Diese Quote ist höher als die Überlebensrate der jungen Fähen in freier Wildbahn, die dort nur $50\,\%$ beträgt.

(2)

$\blacktriangleright$ Existenz einer stationären Verteilung für $\boldsymbol{d=0,1}$ zeigen

Du sollst zeigen, dass es nur für $d=0,1$ eine stationäre Verteilung ungleich dem Nullvektor existiert, das heißt, eine Verteilung $\overrightarrow{s} = \begin{pmatrix}s_1\\s_2\\s_3\end{pmatrix}$ , die folgende Gleichung erfüllt:

$B\cdot \overrightarrow{s} = \overrightarrow{s}$

Es ergibt sich folgendes Gleichungssystem:

$\begin{pmatrix}0&1&d\\0,8&0&0\\0&0,75&0,7\end{pmatrix} \cdot \begin{pmatrix}s_1\\s_2\\s_3\end{pmatrix} =\begin{pmatrix}s_1\\s_2\\s_3\end{pmatrix}$

Mit dem CAS erhältst du als Lösung:

3:Algebra 1:Löse

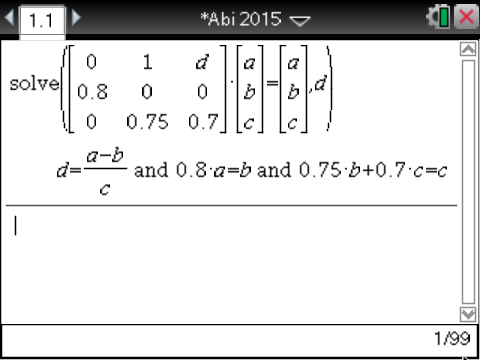Mathematische Gleichungen und Berechnungen auf einem Taschenrechner.

Als Lösung für $d$ erhältst du eine Abhängigkeit von $x_2$ und $x_3$ . Stelle die Gleichung für $x_3$ um und setze sie in die Gleichung für $d$ ein:

$\begin{array}[t]{rll} 15\cdot x_2 + 14\cdot x_3 &=& 20\cdot x_3&\quad&\scriptsize\mid\;-14\cdot x_3\\[5pt] 15\cdot x_2 &=& 6 \cdot x_3 &\quad&\scriptsize\mid\; :6 \\[5pt] 2,5\cdot x_2 &=& x_3\\[5pt] \end{array}$

$\begin{array}[t]{rll} d &=& \dfrac{0,25\cdot x_2}{x_3}\\[5pt] &=& \dfrac{0,25 \cdot x_2}{2,5 \cdot x_2}\\[5pt] &=& 0,1 \end{array}$

Somit gibt es nur für $d=0,1$ eine von $\begin{pmatrix}0\\0\\0\\\end{pmatrix}$ verschiedene stationäre Lösung.

(3)

$\blacktriangleright$ Kleinstmögliche Gesamtpopulation ermitteln

Gesucht ist hier die kleinstmögliche Gesamtpopulation mit stationärer Verteilung, die aus natürlichen Zahlen besteht. Natürliche Zahlen sind alle positiven ganzen Zahlen, also $1$ , $2$ , $3$ .
Eine statrionäre Lösung findest du, indem du die Gleichung aus dem vorherigen Aufgabenteil für $d=0,1$ löst:

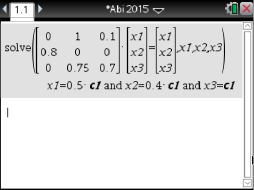Mathematische Gleichungen und Lösungen auf einem Bildschirm dargestellt.

Du erhälst als Lösung: $\overrightarrow{s}_t = \begin{pmatrix} 0,5t \\ 0,4t\\ t\end{pmatrix}$ Damit also alle drei Einträge natürliche Zahlen sind, muss insbesondere $t$ eine natürliche Zahl sein. Zu beachten ist dann noch, dass $t$ die kleinste natürliche Zahl $\neq 0$ ist, sodass $0,4 \cdot t$ und $0,5 \cdot t$ eine natürliche Zahl ist. Um dieses zu finden, schreibe die Kommazahl in einen Bruch um und überlege dir, für welche Faktoren der Bruch verschwindet.

$0,5 t = \frac{1}{2}\cdot t\\ 0,4 t = \dfrac{2}{5}\cdot t$

Du kannst sehen, dass $t$ mindestens $10$ oder ein größeres Vielfaches von davon sein muss, um beide Brüche eliminieren zu können. Daraus folgt, dass die kleinste Gesamtpopulation mit stationärer Verteilung für $t =10$ gegeben ist:

$\overrightarrow{n} = \begin{pmatrix} 5 \\ 4\\ 10\end{pmatrix}$

Die kleinste Gesamtpopulation besteht dann aus $5+4+10 = 19$ Individuen.

Die stationäre Verteilung mit der kleinstmöglichen Gesamtpopulation mit natürlichen Zahlen ist gegeben durch $\overrightarrow{n} = \begin{pmatrix} 5 \\ 4\\ 10\end{pmatrix}$ .

d) (1)

$\blacktriangleright$ Zeigen, dass keine stationäre Verteilung mit 11 Welpen existiert

Hier sollst du nun zeigen, dass in dem neuen Modell mit der Übergangsmatrix $C$ und einer konstanten Gesamtpopulation von $19$ Tieren, keine stationäre Verteilung mit $11$ Welpen möglich ist. Bei einer konstanten Gesamtpopulation von $19$ Tieren und festen Anzahl von $11$ Welpen, ist die Anzahl der Fähen durch $8$ gegeben.

Stelle nun das Gleichungssystem auf, dass sich mit einer stationären Verteilung $\overrightarrow{w} = \begin{pmatrix}11\\8 \end{pmatrix}$ ergibt, berechne damit $h$ und $g$ und überprüfe die Bedingungen, die das Modell an $g$ und $h$ stellt.

$\begin{pmatrix}0& g\\0,8 & h \end{pmatrix} \cdot \begin{pmatrix}11\\8 \end{pmatrix} = \begin{pmatrix}11\\8 \end{pmatrix}$ $\Rightarrow$ $\begin{array}{} \text{I}\quad&11&=&0\cdot 11&+&g\cdot 8&\quad\\ \text{II}\quad&8&=&0,8\cdot 11&+&h\cdot 8&\quad\\ \end{array}$

Die Gleichung $\text{I}$ kannst du direkt nach $g$ auflösen:

$\begin{array}[t]{rll} 11&=&8 \cdot g &\quad \scriptsize \mid\; :8 \\[5pt] \dfrac{11}{8}&=&g \end{array}$

Es gilt $g \gt 0$ , somit ist diese Bedingung des Modells erfüllt. Die Gleichung $\text{II}$ kannst du direkt nach $h$ auflösen:

$\begin{array}[t]{rll} 8&=&0,8\cdot 11+h\cdot 8 &\quad \\[5pt] 8&=& 8,8 + h\cdot 8 &\quad \scriptsize \mid\; -8,8 \\[5pt] -0,8&=& h\cdot 8 &\quad \scriptsize \mid\; :8 \\[5pt] -0,1&=& h \end{array}$

Damit gilt $h\lt 0$ und die Bedingung des Modells an $h$ ist nicht erfüllt. Somit kann in dem neuen Modell keine stationäre Verteilung mit 11 Welpen vorkommen.

(2)

$\blacktriangleright$ Stationäre Verteilung nachweisen

Die Übergangsmatrix $C$ hat mit den für $g$ und $h$ gegebenen Werten folgende Gestalt:

$C = \begin{pmatrix}0&\dfrac{5}{14}\\ 0,8&\dfrac{5}{7}\end{pmatrix}$

Zeige nun, dass durch $\overrightarrow{w} = \begin{pmatrix}5\\14 \end{pmatrix}$ eine stationäre Verteilung gegeben ist. Berechne dazu das Produkt $C \cdot \overrightarrow{w}$ . Erhältst du $\overrightarrow{w}$ als Ergebnis, so hast du eine stationäre Verteilung vorliegen.

$C \cdot \overrightarrow{w}= \begin{pmatrix}0&\dfrac{5}{14}\\ 0,8&\dfrac{5}{7}\end{pmatrix} \cdot \begin{pmatrix}5\\ 14 \end{pmatrix}= \begin{pmatrix}\dfrac{5}{14} \cdot 14 \\ 5 \cdot 0,8 + 14 \cdot \dfrac{5}{7}\end{pmatrix} = \begin{pmatrix}5\\ 4+10\end{pmatrix}=\begin{pmatrix}5\\ 14\end{pmatrix}=\overrightarrow{w}$

Also ist $\overrightarrow{w}$ eine stationäre Verteilung der Matrix $C$ .

(3)

$\blacktriangleright$ Langfristige Entwicklung der Population ermitteln

Hier sollst du die langfristige Entwicklung der neuen Population ermitteln. Bestimme dazu zuerst die aktuelle Verteilung der neuen Population, dann kannst du mit der Matrix $G$ die langfristige Entwicklung dieser Population bestimmen.

Ausgehend von der Verteilung $\overrightarrow{w}=\begin{pmatrix}5\\ 14\\\end{pmatrix}$ sterben nun $5$ Welpen, woraufhin $4$ zusätzliche Fähen angeschafft werden. Damit erhältst du als neue Verteilung $\overrightarrow{w}_{neu}$ :

$\overrightarrow{w}_{neu}=\overrightarrow{w}+\begin{pmatrix}-5\\ 4\end{pmatrix}=\begin{pmatrix}0\\ 18\end{pmatrix}$

Die langfristige Entwicklung kannst du nun mit dem Produkt $G \cdot \overrightarrow{w}_{neu}$ bestimmen:

$G \cdot \overrightarrow{w}_{neu}=\begin{pmatrix}\dfrac{2}{9}&\dfrac{5}{18}\\ \dfrac{28}{45} & \dfrac{7}{9} \end{pmatrix} \cdot \begin{pmatrix}0\\ 18\end{pmatrix}=\begin{pmatrix}\dfrac{5}{18} \cdot 18\\ \dfrac{7}{9} \cdot 18\end{pmatrix}=\begin{pmatrix}5\\ 14\end{pmatrix}$

Damit entwickelt sich die neue Population langfristig gegen die ursprüngliche Verteilung $\overrightarrow{w}$ .

a) (1)

$\blacktriangleright$ Wert für $\boldsymbol{b}$ begründen

$b = \dfrac{j_{2014}}{w_{2013}} = \dfrac{26}{65} = 0,4\qquad$ Grünes Häkchen-Symbol auf transparentem Hintergrund.

(2)

$\blacktriangleright$ Einträge der Matrix interpretieren

Eintrag $\boldsymbol{a_{1,2} = 1,5}$ :

Eintrag $\boldsymbol{a_{3,2} = 0,5}$ :

Eintrag $\boldsymbol{a_{1,3} = 2}$ :

Analog zum ersten Eintrag in der zweiten Spalte, gibt der erste Eintrag der dritten Spalte die Anzahl der Welpen an, die jede ausgewachsene Fähe im Schnitt pro Jahr bekommt.

Eintrag $\boldsymbol{a_{3,3} = 0,6}$ :

Dieser Eintrag gibt die Übergangsquote von ausgewachsener Fähe zu ausgewachsener Fähe an. Dies entspricht der Überlebensrate der ausgewachsenen Fähen.

b) (1)

$\blacktriangleright$ Verteilung der nächsten Jahre berechnen

Den Verteilungsvektor $\overrightarrow{v}_i$ , der die Verteilung der Population im $i$ -ten Entwicklungsschritt beschreibt, lässt sich allgemein über folgende Formel berechnen:

$\overrightarrow{v}_i = A \cdot \overrightarrow{v}_{i-1} = A^{i}\cdot \overrightarrow{v}_0$

Dabei ist $A$ die betrachtete Übergangsmatrix.

$\overrightarrow{v}_{2014} = \begin{pmatrix}52\\26\\16\end{pmatrix}$

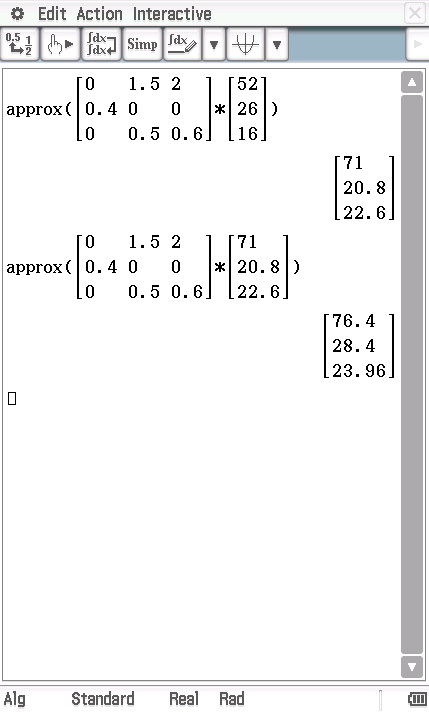Mathematische Berechnungen mit Matrizen und Approximationen in einer Softwareanwendung.

Es ergibt sich:

$\begin{array}[t]{rll} \vec{v_{2015}}&=&\begin{pmatrix}71\\20,8\\22,6\\\end{pmatrix}\; , \vec{v_{2016}}&=&\begin{pmatrix}76,4\\28,4\\23,96\\\end{pmatrix}\\ \end{array}$

(2)

$\blacktriangleright$ Verteilung vom Vorjahr berechnen

$\overrightarrow{v}_{2012} = A^{-1}\cdot \overrightarrow{v}_{2013}$

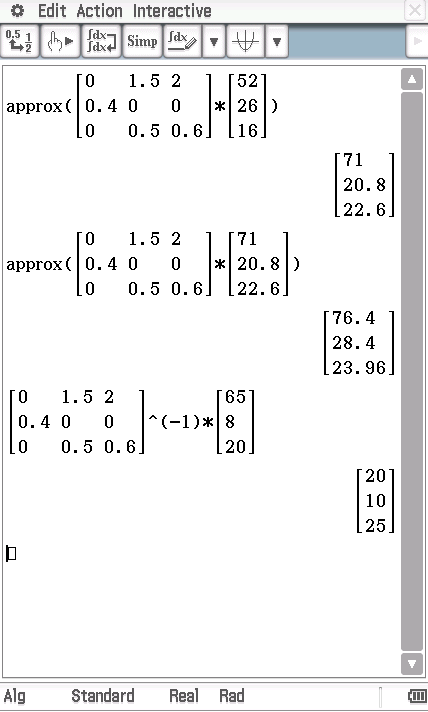Mathematische Ausdrücke und Matrizen in einer Software-Oberfläche.

Damit gilt nun $\overrightarrow{v}_{2012} = \begin{pmatrix}v_1\\v_2\\v_3\end{pmatrix} = \begin{pmatrix}20\\10\\25\end{pmatrix}$ .

Nach dem Modell hätte im Jahr 2012 eine Verteilung mit $20$ Welpen, $10$ jungen Fähen und $25$ ausgewachsenen Fähen vorgelegen.

(3)

$\blacktriangleright$ Zeigen, dass sich die Population aus 2011 nicht bestimmen lässt

Die Verteilung aus dem Jahr 2012 hast du aus dem vorherigen Aufgabenteil gegeben:

$\overrightarrow{v}_{2012} = \begin{pmatrix}20\\10\\25\end{pmatrix}$

Damit kannst du nun wie im vorherigen Aufgabenteil die Verteilung aus dem vorigen Jahr mit deinem CAS bestimmen:

Mathematische Berechnungen und Matrixoperationen in einer Softwareanwendung.

Damit gilt nun $\overrightarrow{v}_{2011} = \begin{pmatrix}v_1\\v_2\\v_3\end{pmatrix} = \begin{pmatrix}25\\380\\-275\end{pmatrix}$ .

Da die dritte Komponente negativ ist und eine Population nur positive Werte besitzt, kann durch das Modell nicht die Population im Jahr 2011 beschrieben werden.

(4)

$\blacktriangleright$ Prozentsatz berechnen

Um die Behauptung des Biologen zu überprüfen, berechne den Prozentsatz der Welpen, die ein Alter von mindestens drei Jahren erreichen mit Hilfe der Pfadmultiplikationsregel.

Mit der Pfadmultiplikationsregel ergibt sich dementsprechend folgender Prozentsatz:

$p = 0,4\cdot 0,5\cdot 0,6 = 0,12 = 12\,\%$ .

Nach dem angegebenen Modell mit der Matrix A erreichen durchschnittlich $12\,\%$ aller Welpen mindestens ein Alter von $3$ Jahren. Die Behauptung des Biologen trifft nach diesem Modell demnach zu.

c) (1)

$\blacktriangleright$ Einträge im Sachzusammenhang vergleichen

Eintrag $\boldsymbol{b_{1,2} = 1}$ :

Eintrag $\boldsymbol{b_{2,2} = 0}$ :

Eintrag $\boldsymbol{b_{3,2} = 0,75}$ :

(2)

$\blacktriangleright$ Existenz einer stationären Verteilung für $\boldsymbol{d=0,1}$ zeigen

$B\cdot \overrightarrow{s} = \overrightarrow{s}$

Es ergibt sich folgendes Gleichungssystem:

$\begin{pmatrix}0&1&d\\0,8&0&0\\0&0,75&0,7\end{pmatrix} \cdot \begin{pmatrix}s_1\\s_2\\s_3\end{pmatrix} =\begin{pmatrix}s_1\\s_2\\s_3\end{pmatrix}$

Stellst du das Gleichungssystem um und löst nach $d$ auf, erhältst du:

$\begin{array}{} \text{I}\quad&s_1&=&s_2+d\cdot s_3\quad\\[5pt] \text{II}\quad&s_2&=&0,8\cdot s_1\quad\\[5pt] \text{III}\quad&s_3&=& 0,75\cdot s_2 + 0,7\cdot s_3&\quad&\scriptsize\mid\;-0,7\cdot s_3\\[5pt] &0,3\cdot s_3&=& 0,75\cdot s_2&\quad&\scriptsize\mid\;:0,3\\[5pt] \text{IIIa}\quad&s_3&=&2,5\cdot s_2&\quad& \scriptsize\mid\;\text{Setze: IIIa in I}\\[5pt] \text{Ia}\quad&s_1&=&s_2+d\cdot 2,5\cdot s_2&\quad& \scriptsize\mid\;\text{Setze: II in Ia}\\[5pt] &s_1&=&0,8\cdot s_1+2,5\cdot d \cdot 0,8 \cdot s_1&\quad&\scriptsize\mid\; -0,8\cdot s_1\\[5pt] &0,2\cdot s_1 &=& 2\cdot d \cdot s_1&\quad&\scriptsize\mid\;:2\cdot s_1\\[5pt] &0,1&=&d\quad\\[5pt] \end{array}$

Somit gibt es nur für $d=0,1$ eine von $\begin{pmatrix}0\\0\\0\\\end{pmatrix}$ verschiedene stationäre Lösung.

(3)

$\blacktriangleright$ Kleinstmögliche Gesamtpopulation ermitteln

Gesucht ist hier die kleinstmögliche Gesamtpopulation mit stationärer Verteilung, die aus natürlichen Zahlen besteht. Natürliche Zahlen sind alle positiven ganzen Zahlen, also $1$ , $2$ , $3$ .
Eine stationäre Lösung findest du, wenn du das Gleichungssystem aus dem vorherigen Aufgabenteil für $d=0,1$ löst. Setze dazu $s_1=t$ :

$\begin{array}[t]{rll} s_1&=&t\\[5pt] s_2&=& 0,8 t\\[5pt] s_3&=& 0,75 \cdot 0,8 t + 0,7 s_3\quad\scriptsize\mid\; -0,7 s_3\\[5pt] 0,3 s_3 &=& 0,6 t \quad\scriptsize\mid\; :0,3\\[5pt] s_3 &=& 2 t \\[5pt] \end{array}$

Als Lösung ergibt sich: $\vec{s}=\begin{pmatrix}t\\0,8t\\2t\\\end{pmatrix}$ . Damit also alle drei Einträge natürliche Zahlen sind, muss insbesondere $t$ eine natürliche Zahl sein. Zu beachten ist dann noch, dass $t$ die kleinste natürliche Zahl $\neq 0$ ist, sodass $0,8 \cdot t$ eine natürliche Zahl ist. Um dieses zu finden, schreibe die Kommazahl in einen Bruch um und überlege dir, für welche Faktoren der Bruch verschwindet.

$0,8 t = \frac{4}{5}\cdot t$

Du kannst sehen, dass $t$ mindestens $5$ oder ein größeres Vielfaches von $5$ sein muss, um den Bruch eliminieren zu können. Daraus folgt, dass die kleinste Gesamtpopulation mit stationärer Verteilung für $t =5$ gegeben ist:

$\overrightarrow{n} = \begin{pmatrix} 5 \\ 4\\ 10\end{pmatrix}$

Die kleinste Gesamtpopulation besteht dann aus $5+4+10 = 19$ Individuen.

Die stationäre Verteilung mit der kleinstmöglichen Gesamtpopulation mit natürlichen Zahlen ist gegeben durch $\overrightarrow{n} = \begin{pmatrix} 5 \\ 4\\ 10\end{pmatrix}$ .

d) (1)

$\blacktriangleright$ Zeigen, dass keine stationäre Verteilung mit 11 Welpen existiert

Die Gleichung $\text{I}$ kannst du direkt nach $g$ auflösen:

$\begin{array}[t]{rll} 11&=&8 \cdot g &\quad \scriptsize \mid\; :8 \\[5pt] \dfrac{11}{8}&=&g \end{array}$

Es gilt $g \gt 0$ , somit ist diese Bedingung des Modells erfüllt. Die Gleichung $\text{II}$ kannst du direkt nach $h$ auflösen:

$\begin{array}[t]{rll} 8&=&0,8\cdot 11+h\cdot 8 &\quad \\[5pt] 8&=& 8,8 + h\cdot 8 &\quad \scriptsize \mid\; -8,8 \\[5pt] -0,8&=& h\cdot 8 &\quad \scriptsize \mid\; :8 \\[5pt] -0,1&=& h \end{array}$

Damit gilt $h\lt 0$ und die Bedingung des Modells an $h$ ist nicht erfüllt. Somit kann in dem neuen Modell keine stationäre Verteilung mit 11 Welpen vorkommen.

(2)

$\blacktriangleright$ Stationäre Verteilung nachweisen

Die Übergangsmatrix $C$ hat mit den für $g$ und $h$ gegebenen Werten folgende Gestalt:

$C = \begin{pmatrix}0&\dfrac{5}{14}\\ 0,8&\dfrac{5}{7}\end{pmatrix}$

Also ist $\overrightarrow{w}$ eine stationäre Verteilung der Matrix $C$ .

(3)

$\blacktriangleright$ Langfristige Entwicklung der Population ermitteln

$\overrightarrow{w}_{neu}=\overrightarrow{w}+\begin{pmatrix}-5\\ 4\end{pmatrix}=\begin{pmatrix}0\\ 18\end{pmatrix}$

Die langfristige Entwicklung kannst du nun mit dem Produkt $G \cdot \overrightarrow{w}_{neu}$ bestimmen:

Damit entwickelt sich die neue Population langfristig gegen die ursprüngliche Verteilung $\overrightarrow{w}$ .