Aufgabe 1
a)
Gegeben sind die in 
definierten Funktionen 
und 
Die Graphen von 
und 
haben genau einen gemeinsamen Punkt; dieser Punkt liegt auf der 
-Achse. Für die erste Ableitungsfunktion von gilt 
(1)
Beschreibe, wie der Graph von 
aus dem Graphen von erzeugt werden kann.
(2)
Zeige, dass die Graphen von und in ihrem gemeinsamen Punkt eine gemeinsame Tangente haben, und gib eine Gleichung dieser Tangente an.
(3)
Gib den Wert des Integrals 
an und interpretiere diesen Wert geometrisch.
(2 + 3 + 3 Punkte)
b)
Gegeben ist die in definierte Funktion 
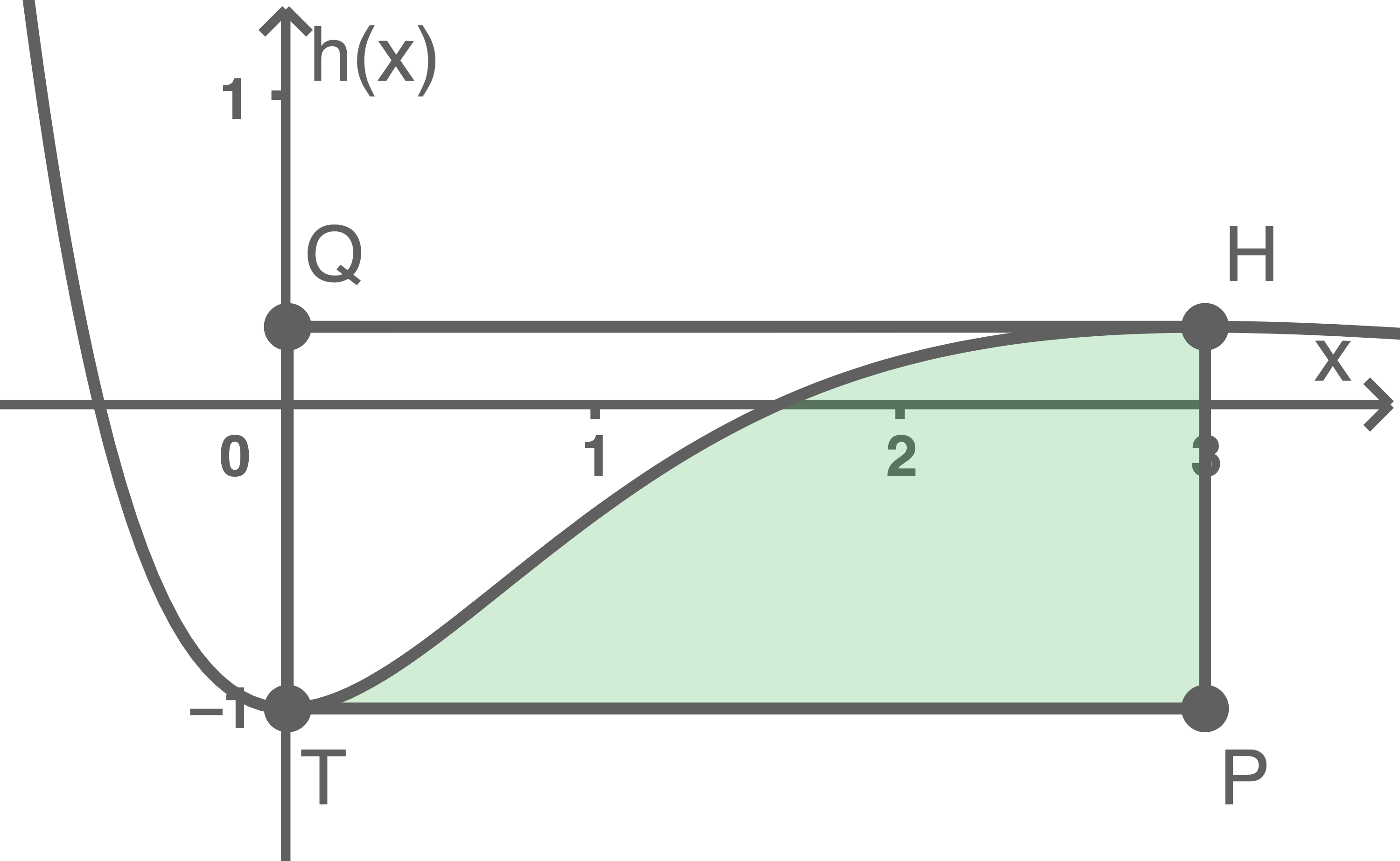Ermittle, welchen Anteil an der Fläche des Rechtecks die Fläche des markierten Teilstücks einnimmt.
(1)
Bestimme die Größe der Fläche, die der Graph von 
und die 
-Achse einschließen.
(2)
Berechne die Koordinaten der beiden Extrempunkte des Graphen von sowie den Abstand der Extrempunkte.
(3)
Die beiden Extrempunkte 
und 
des Graphen von bilden zusammen mit den Punkten 
und 
ein Rechteck 
dessen Seiten parallel zu den Koordinatenachsen verlaufen. Dieses Rechteck wird durch den Graphen der Funktion in zwei Teilstücke zerlegt (siehe Abbildung 1).
Abbildung 1
(3 + 4 + 6 Punkte)
c)
Ein Bewässerungskanal wird durch Öffnen einer Schleuse in Betrieb genommen.
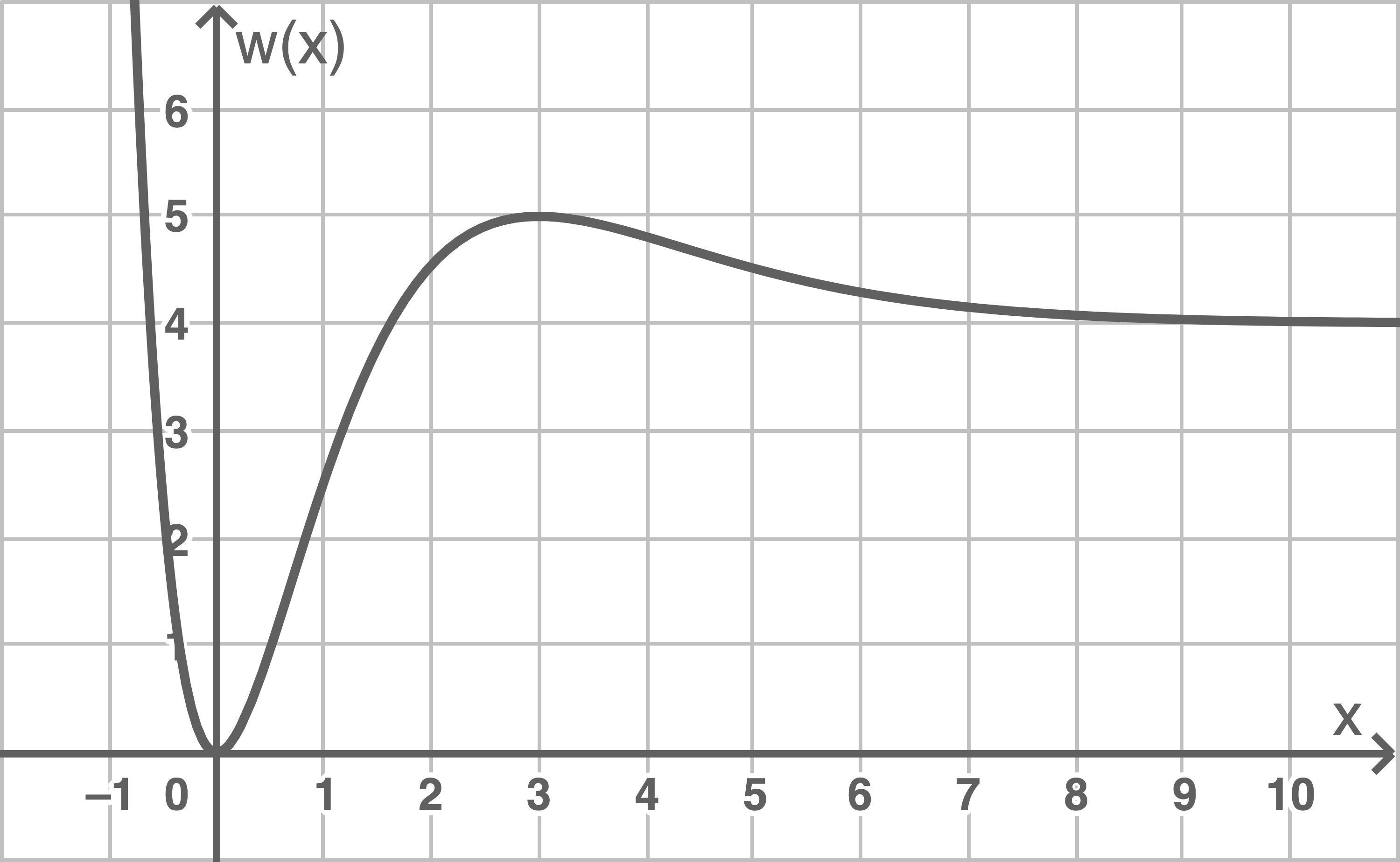Abbildung 2 zeigt den Graphen von 
Die in definierte Funktion 
beschreibt für 
die zeitliche Entwicklung der momentanen Durchflussrate des Wassers an einer Messstelle. Dabei ist die seit Beobachtungsbeginn vergangene Zeit in Sekunden und 
die momentane Durchflussrate in Kubikmetern pro Sekunde.
Abbildung 2
(1)
Für 
gilt 
Gib den Wert 
sowie die Bedeutung dieses Wertes im Sachzusammenhang an.
(2)
Bestimme diejenigen Stellen, an denen die momentane Änderungsrate der Funktion 
mit der mittleren Änderungsrate der Funktion über dem Intervall ![\([0 ; 10]\)](https://mathjax.schullv.de/7b49918e86e7ec9238d1bd1114b2feb0629a829792a39542bfbe25f1f66a2334?color=5a5a5a)
übereinstimmt.
(3)
Bestimme die momentane Durchflussrate für denjenigen Zeitpunkt in den ersten zehn Sekunden nach Beobachtungsbeginn, zu dem sie am stärksten abnimmt.
(4)
(i)
Bestimme die Wassermenge, die in den ersten zwei Sekunden seit Beobachtungsbeginn an der Messstelle vorbeifließt.
(ii)
An der Messstelle fließen in einem Zeitraum von drei Sekunden dreizehn Kubikmeter Wasser vorbei. Berechne die dafür infrage kommenden Zeiträume.
(2 + 3 + 3 + 6 Punkte)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
(1)
Der Graph von kann aus dem Graphen von durch eine Spiegelung an der -Achse erzeugt werden.
(2)
1. Schritt: Koordinaten des gemeinsamen Punktes ermitteln
Da der gemeinsame Punkt auf der -Achse liegt, gilt 
Die Koordinaten des gemeinsamen Punktes lauten 
2. Schritt: Nachweis der gemeinsamen Tangente
Damit die Graphen von 
und 
eine gemeinsame Tangente im Punkt haben, müssen sie in diesem Punkt die gleiche Steigung haben. Die Steigungen werden mit der jeweiligen ersten Ableitungsfunktion berechnet.
Mit 
und 
liegt in eine gemeinsame Tangente vor.
3. Schritt: Gleichung der gemeinsamen Tangente angeben
Für die Steigung der Tangente gilt 
Da auf der -Achse liegt, folgt 
Die Gleichung der Tangente lautet somit 
(3)
Wert des Integrals angeben
Mit dem CAS ergibt sich:
Geometrische Interpretation
Die Fläche, die die Graphen von und sowie die Gerade mit der Gleichung 
einschließen, hat einen Inhalt von ca. 3,53 Flächeneinheiten.
b)
(1)
Schnittstellen des Graphen von mit der -Achse bestimmen
Die Gleichung 
wird mit dem solve-Befehl des CAS gelöst.
Es ergeben sich 
und 
Inhalt der eingeschlossenen Fläche bestimmen
![\(\begin{array}[t]{rll}
A&=& \left|\displaystyle\int_{x_1}^{x_2} h(x) \;\mathrm d x\right| \\[5pt]
&=&\left|\displaystyle\int_{-0,62}^{1,62} h(x) \;\mathrm d x\right|
\end{array}\)](https://mathjax.schullv.de/a6bb0f38e5ecb5f7e1a1c6308e843341eea688c8662eaa76be887ac7ce66d59b?color=5a5a5a)
Der Wert des Integrals ergibt sich mit dem CAS und somit auch die Größe der Fläche, die der Graph von und die -Achse einschließen: ![\(A \approx 1,28 \;\text{[FE]}\)](https://mathjax.schullv.de/51861a6bbc3d8d3853fd41a274ae0d85f3b4cc5a563b2755e85fdc64bf5cddc2?color=5a5a5a)
(2)
Koordinaten der Extrempunkte berechnen
Notwendige Bedingung für Extremstellen anwenden:
![\(\begin{array}[t]{rll}
h](https://mathjax.schullv.de/16ccc0483cf775443c0e1eb0370bafa62829aa383e66f42eeda68582f725743d?color=5a5a5a)
Mit dem solve-Befehl des CAS folgen 
und 
als Lösungen der Gleichung.
Da 
nur zwei Nullstellen besitzt, muss es sich um die Extremstellen handeln. Damit kann auf die Überprüfung der hinreichenden Bedingung für Extremstellen verzichtet werden.
Die Koordinaten der Extrempunkte folgen zu 
und 
Abstand der Extrempunkte berechnen
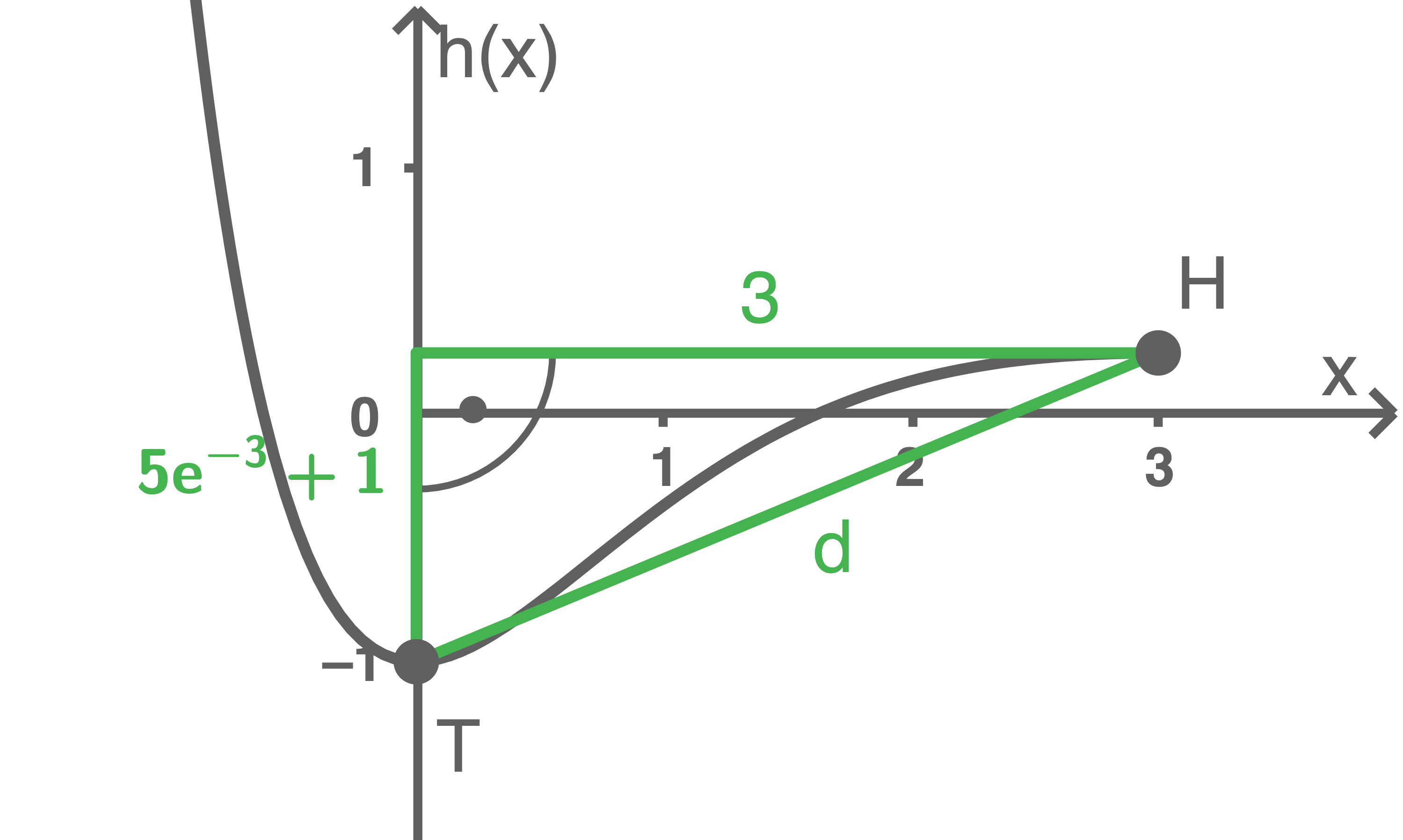
Hilfsskizze zum besseren Verständnis
Mit dem Satz des Pythagoras ergibt sich:
![\(\begin{array}[t]{rll}
d^2&=& 3^2+(5\mathrm e^{-3}+1)^2 &\quad \scriptsize \mid\;\sqrt{\;} \\[5pt]
d&=& \sqrt{3^2+(5\mathrm e^{-3}+1)^2} \\[5pt]
&\approx & 3,25 \;\text{[LE]}
\end{array}\)](https://mathjax.schullv.de/c2dde8e166cdfbc9463a4b7ecfdee38d4f592105b6b778e7b6272d53d1b4d86b?color=5a5a5a)
(3)
1. Schritt: Flächeninhalt des Rechtecks 
bestimmen
Aus den Längen der Seiten folgt:
![\(A_{TPHQ}=3 \cdot\left(5 \mathrm e ^{-3}+1\right) \approx 3,75\;\text{[FE]}\)](https://mathjax.schullv.de/a1e612756585d77764190e213448813c0e554fb36423fe14a47d79169a83a6ce?color=5a5a5a)
2. Schritt: Flächeninhalt des markierten Teilstücks bestimmen
Markiert ist die Fläche zwischen dem Graphen von und der Geraden mit der Gleichung 
über dem Intervall ![\([0;3].\)](https://mathjax.schullv.de/ae81ad62ff01d210aa85cd93f9726f052509c2ea967506e65c8c868add7e3d36?color=5a5a5a)
Ihr Inhalt entspricht dem Wert folgenden Integrals, welches mit Hilfe des CAS bestimmt wird:
3. Schritt: Anteil ermitteln
Somit nimmt das markierte Teilstück einen Anteil von ca. 
an der Fläche des Rechtecks ein.
c)
(1)
Ablesen aus Abbildung 2: Es ist 
Im Sachzusammenhang bedeutet dies, dass sich die momentane Durchflussrate langfristig einem Wert von 
annähert.
(2)
Die momentane Änderungsrate ergibt sich mit dem CAS zu 
Die mittlere Änderungsrate der Funktion über dem Intervall ![\([0;10]\)](https://mathjax.schullv.de/d8eeb4818039bb69f6a7765f496e726747007838c92f84f8227eeb9ef0f7e11f?color=5a5a5a)
entspricht 
Gleichsetzen:
![\(\begin{array}[t]{rll}
w](https://mathjax.schullv.de/04f9accac35d55d48c384edc03a5e97fafce1e4eae8cc23181db4dc28d9bb1f6?color=5a5a5a)
Mit dem solve-Befehl des CAS ergeben sich 
und 
(3)
Die stärkste Abnahme liegt an derjenigen Wendestelle 
des Graphen von vor, für die 
gilt.
Mit dem CAS ergeben sich die Koordinaten des Tiefpunktes von 
zu 
Damit liegt die stärkste Abnahme der momentanen Durchflussrate in den ersten zehn Sekunden nach Beobachtungsbeginn ungefähr 4,3 Sekunden nach Beobachtungsbeginn vor.
(4)
(i)
(ii)