NRW Abi 2025 Mathe GK GTR Teil A Pflichtteil Aufgaben Q1/Q2

1

Gegeben ist die in $\mathbb R$ definierte Funktion $f$ mit

$f(x)=\dfrac{1}{8}x^3-\dfrac{3}{8}x^2-1.$

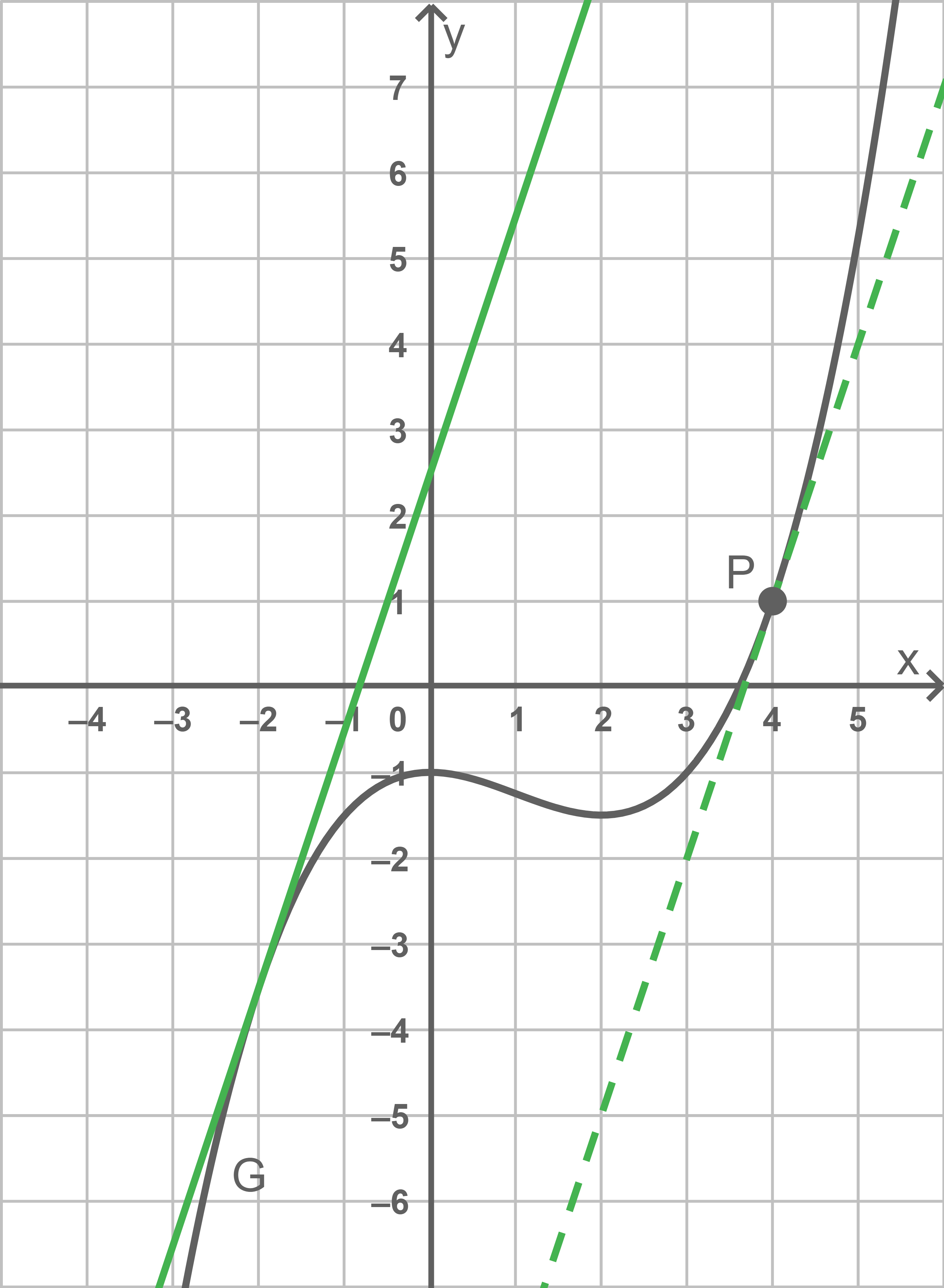
Abbildung 1 zeigt den Graphen $G$ von $f.$

Die Tangente an $G$ im Punkt $P(4\mid 1)$ wird mit $t$ bezeichnet.

(1)

Bestimme rechnerisch eine Gleichung von $t.$

(2)

Es gibt genau eine weitere Tangente an $G,$ die parallel zu $t$ verläuft.

Skizziere diese in der Abbildung.

Abbildung 1

(3+2 Punkte)

2

Gegeben ist die Gerade $g: \overrightarrow{x}=\pmatrix{8\\3\\-3}+s \cdot\pmatrix{-4\\0\\3}$ mit $s \in \mathbb{R}.$

(1)

Zeige, dass der Punkt $P(4\mid3\mid 3)$ nicht auf $g$ liegt.

Gib die Koordinaten eines Punktes $Q$ an, der auf $g$ liegt und sich nur in einer Koordinate von $P$ unterscheidet.

(2)

Die Gerade $h$ verläuft parallel zur $y$ -Achse und schneidet $g$ im Punkt $(8\mid3\mid-3).$

Untersuche, ob $g$ und $h$ senkrecht zueinander verlaufen.

(3+2 Punkte)

3

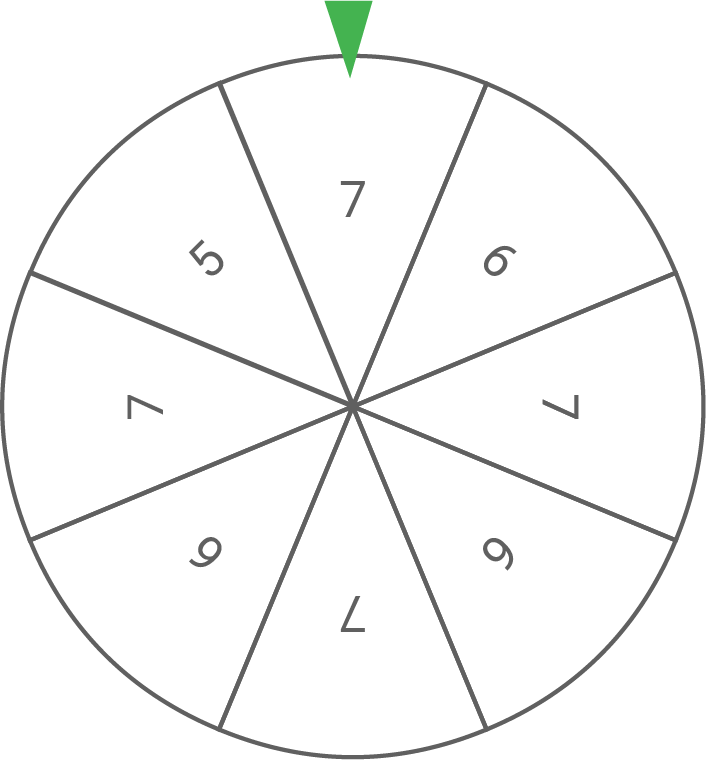
Ein Glücksrad mit acht gleichgroßen Sektoren ist wie abgebildet beschriftet. Das Glücksrad wird zweimal gedreht.

(1)

Interpretiere den Term $\left(\dfrac{3}{8}\right)^2$ im Sachzusammenhang.

(2)

Berechne die Wahrscheinlichkeit dafür, dass die Summe der erzielten Zahlen ungerade ist.

Abbildung

Abbildung 2

(2+3 Punkte)

Pflichtteil