Aufgabe 1
Aufgabenstellung
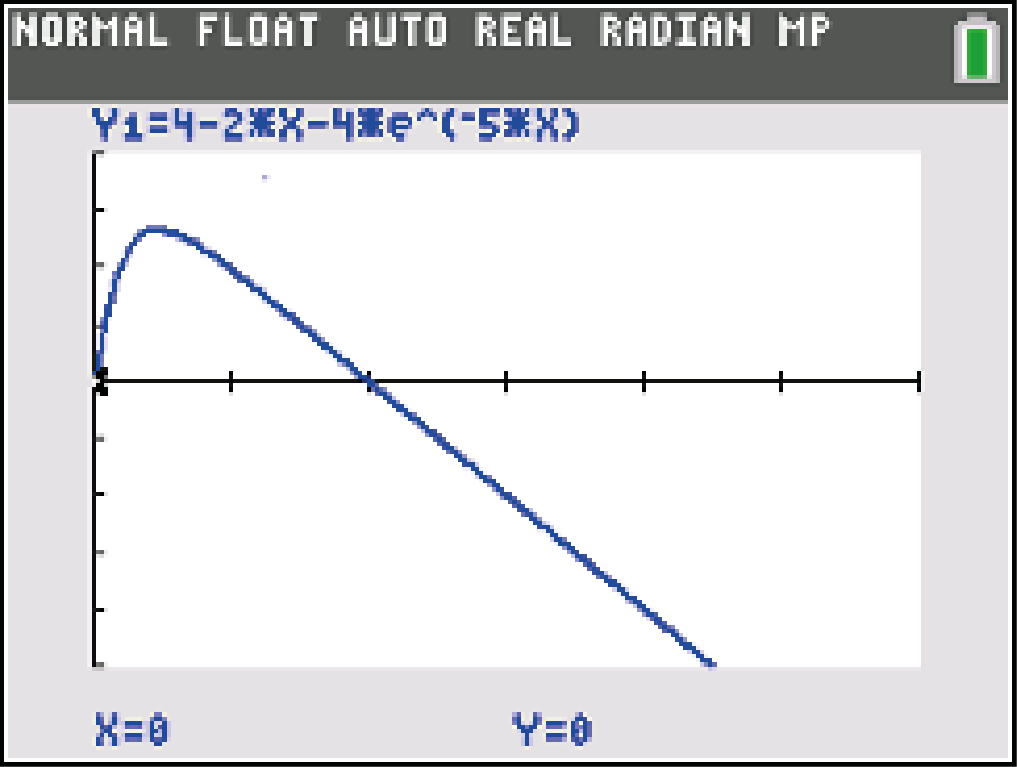
Die Funktion  ist gegeben durch die Gleichung
ist gegeben durch die Gleichung  ,
,  .
.
 sei die Gerade mit der Gleichung
sei die Gerade mit der Gleichung  ,
, .
.
a)
(1)
Berechne die Koordinaten des Schnittpunkts des Graphen von  mit der
mit der  -Achse.
-Achse.
(2P)
(2)
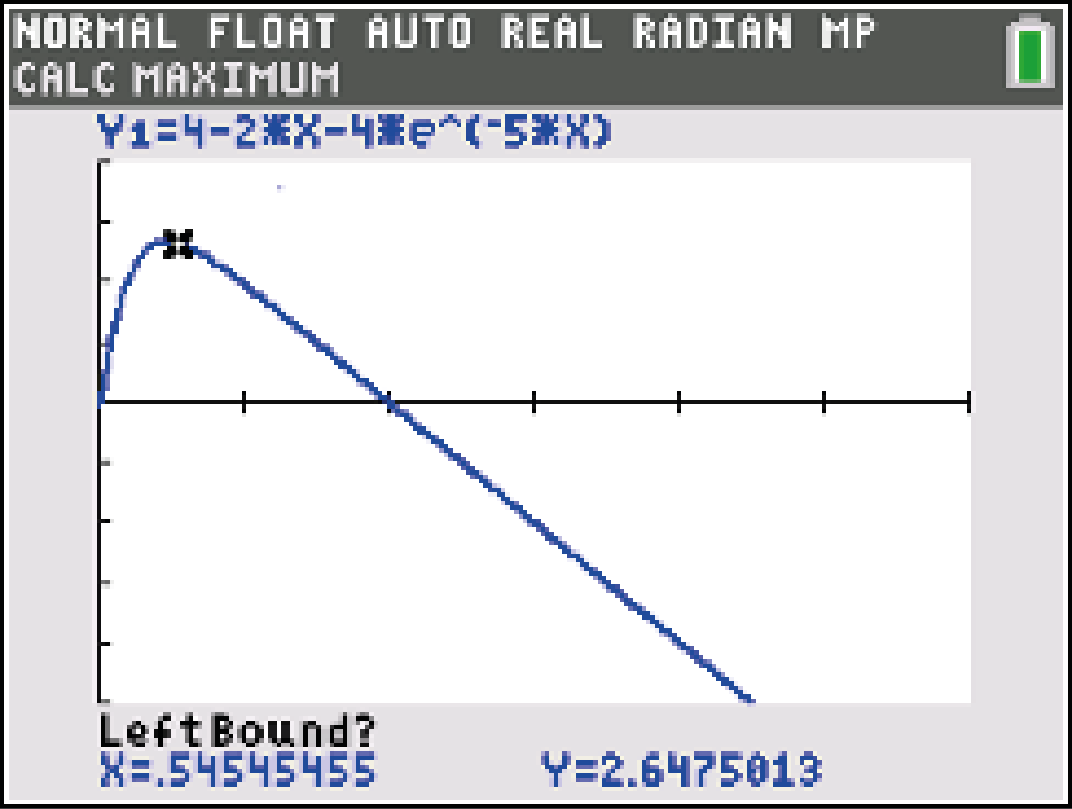
Bestimme die lokale Maximalstelle  der Funktion
der Funktion  .
.
[Zur Kontrolle: ;
;  ]
]
[Zur Kontrolle:
(9P)
b)
(1)
Begründe, dass die Ableitungsfunktion  streng monoton fallend ist.
streng monoton fallend ist.
(3P)
(2)
Bestimme das Monotonieverhalten der Funktion  .
.
(4P)
(3)
Begründe nun, dass die Funktion  höchstens zwei Nullstellen besitzt.
höchstens zwei Nullstellen besitzt.
(3P)
c)
(1)
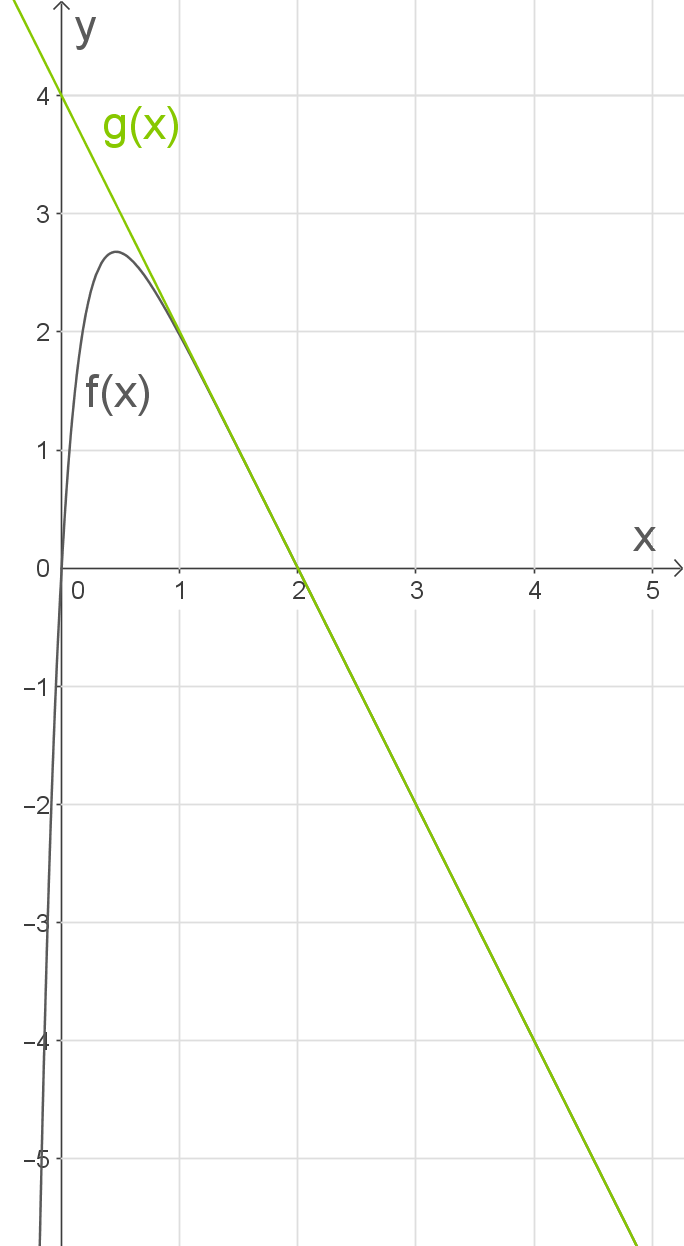
Zeichne die Gerade  in die Abbildung ein.
in die Abbildung ein.
(2P)
(2)
Zeige:
Für alle verläuft der Graph der Funktion
verläuft der Graph der Funktion  unterhalb der Geraden
unterhalb der Geraden  .
.
Für alle
(3P)
(3)
Begründe mit Hilfe von c) (2):
Wenn eine Nullstelle der Funktion
eine Nullstelle der Funktion  ist, dann gilt
ist, dann gilt  .
.
Wenn
(4P)
(4)
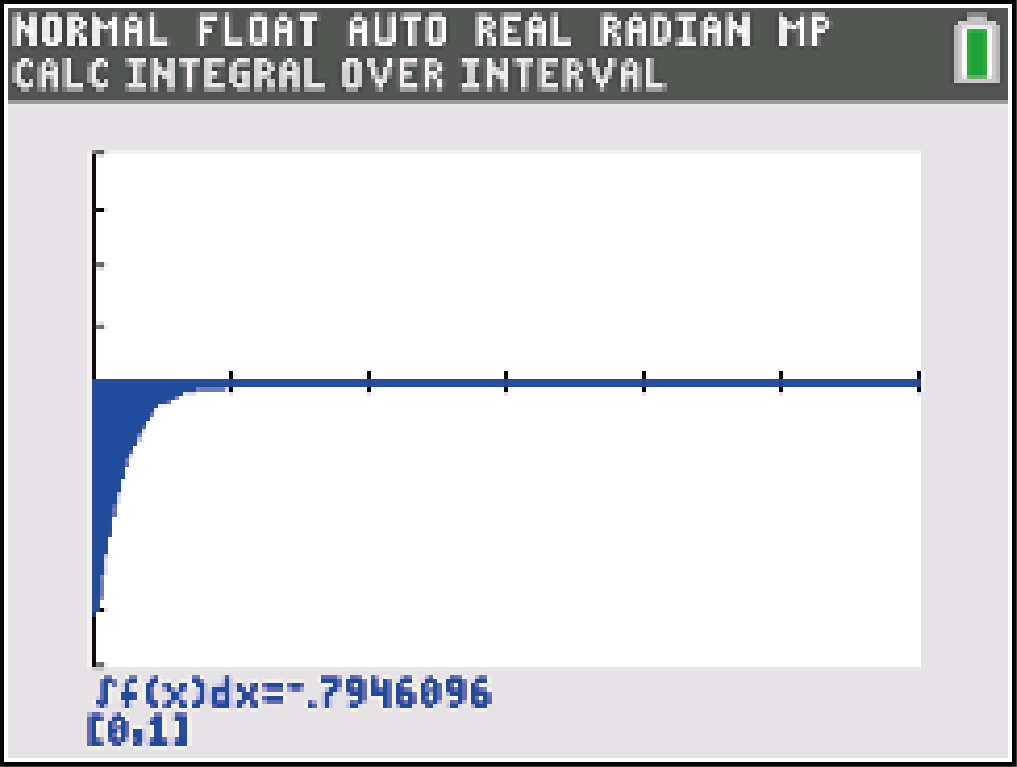
Zwischen der Geraden  und dem Graphen der Funktion
und dem Graphen der Funktion  ist im Intervall
ist im Intervall ![\( [0; 1]\)](https://www.schullv.de/resources/formulas/0aee421530508442657d40113934c2e547880f72aa3ed5e873c585ca4f007ba0_light.svg) eine Fläche eingeschlossen.
eine Fläche eingeschlossen.
Berechne den Inhalt dieser Fläche.
Berechne den Inhalt dieser Fläche.
(5P)
d)
Im Rahmen eines schulischen Projekts untersucht ein Schüler, wie stark ein Ball aus Styropor beim Wurf von der Luft abgebremst wird.
Dazu lehnt er sich aus einem Fenster der Schule und wirft den Ball senkrecht nach oben. Dabei zeichnet eine Kamera die Bewegung des Balles auf, bis dieser unten auf den Boden trifft. Er stellt fest, dass die Bewegung des Balles für durch die oben gegebene Funktion
durch die oben gegebene Funktion  modelliert werden kann. Dabei wird
modelliert werden kann. Dabei wird  als Maßzahl der Zeit zur Einheit
als Maßzahl der Zeit zur Einheit  und
und  als Maßzahl der Höhe des Balles zur Einheit
als Maßzahl der Höhe des Balles zur Einheit  aufgefasst.
aufgefasst.
Die Höhe des Balles bezieht sich auf die Abwurfhöhe
![\( [\text{m}]\)](https://www.schullv.de/resources/formulas/295b0b4ee3a2d0c0cbc103c770ed34f832950ba9c1b5adc3a522865833ee3d1d_light.svg) zur Zeit
zur Zeit 
![\( [\text{s}]\)](https://www.schullv.de/resources/formulas/14001ce945516b559c3cf608975435ea020afeb6354c73bd66009e4308c8adac_light.svg) .
.
Bildnachweise [nach oben]
Dazu lehnt er sich aus einem Fenster der Schule und wirft den Ball senkrecht nach oben. Dabei zeichnet eine Kamera die Bewegung des Balles auf, bis dieser unten auf den Boden trifft. Er stellt fest, dass die Bewegung des Balles für
Die Höhe des Balles bezieht sich auf die Abwurfhöhe
(1)
Nach 
 trifft der Ball auf den Boden.
trifft der Ball auf den Boden.
Berechne, in welcher Höhe über dem Boden der Ball abgeworfen wurde.
Berechne, in welcher Höhe über dem Boden der Ball abgeworfen wurde.
(2P)
(2)
Bestimme die maximale Höhe des Balles über dem Boden.
(3P)
(3)
Begründe durch den Sachzusammenhang, dass die Funktion  im Zeitintervall
im Zeitintervall ![\( [0; 5]\)](https://www.schullv.de/resources/formulas/cf6e8c27b081baccafe107cfe630a5f0d42bb00bed602e8d90a480f1f68acdd7_light.svg) genau zwei Nullstellen besitzt.
genau zwei Nullstellen besitzt.
Gib diese Nullstelle auf zwei Nachkommastellen genau an.
Gib diese Nullstelle auf zwei Nachkommastellen genau an.
(5P)
(4)
Berechne das Maximum und das Minimum der Funktion  im Zeitintervall
im Zeitintervall ![\( [0; 5]\)](https://www.schullv.de/resources/formulas/cf6e8c27b081baccafe107cfe630a5f0d42bb00bed602e8d90a480f1f68acdd7_light.svg) und interpretiere deine Ergebnisse im Sachzusammenhang.
und interpretiere deine Ergebnisse im Sachzusammenhang.
(5P)
© 2016 - SchulLV.
a)
(1)
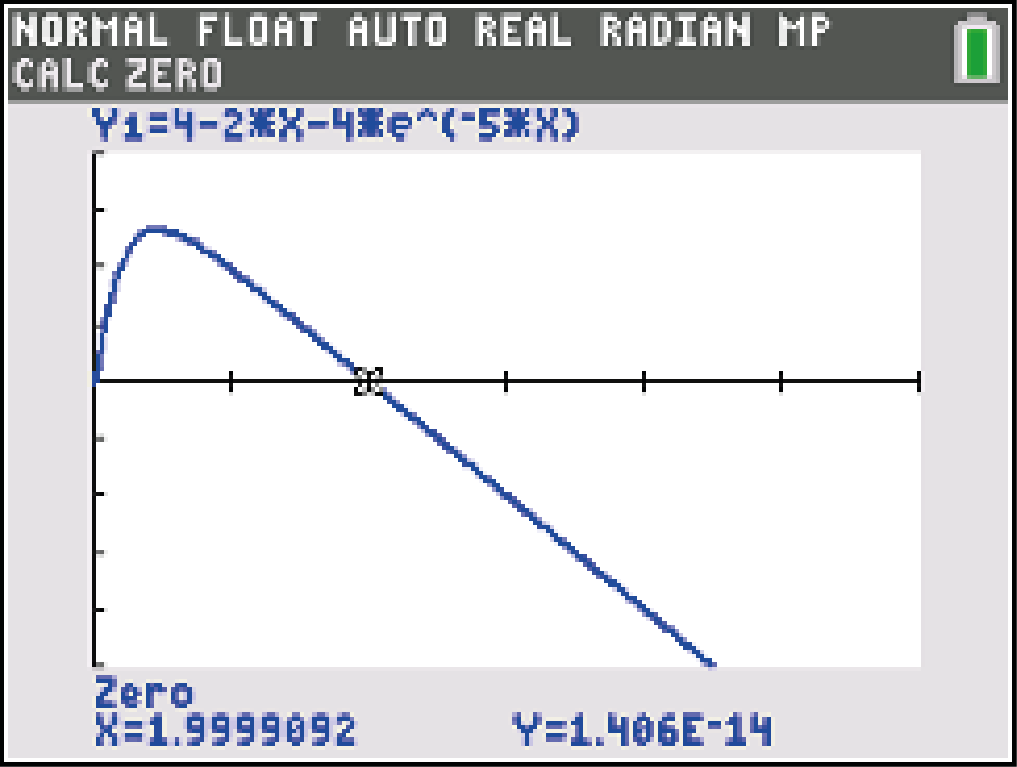
2ND  F4: CALC
F4: CALC  1: value
1: value
den Schnittpunkt mit der
(2)
- Notwendiges Kriterium:
- Hinreichendes Kriterium:
- Ableitungen
und
von der Funktion
berechnen.
- Berechne mit Hilfe des notwendigen Kriteriums die
-Koordinate.
- Prüfe das hinreichende Kriterium.
2ND  F4: CALC
F4: CALC  4: maximum
4: maximum
die Maximalstelle
b)
(1)
(2)
(3)
c)
(1)
(2)
(3)
(4)
2ND  F4: CALC
F4: CALC  7:
7: 
den Flächeninhalt der Fläche zwischen der Geraden
d)
(1)
(2)
(3)
2ND  F4: CALC
F4: CALC  1: zero.
1: zero.
Hierbei musst du nun noch einen Bereich wählen, indem sich die Nullstelle befindet.
(4)
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
a)
(1)
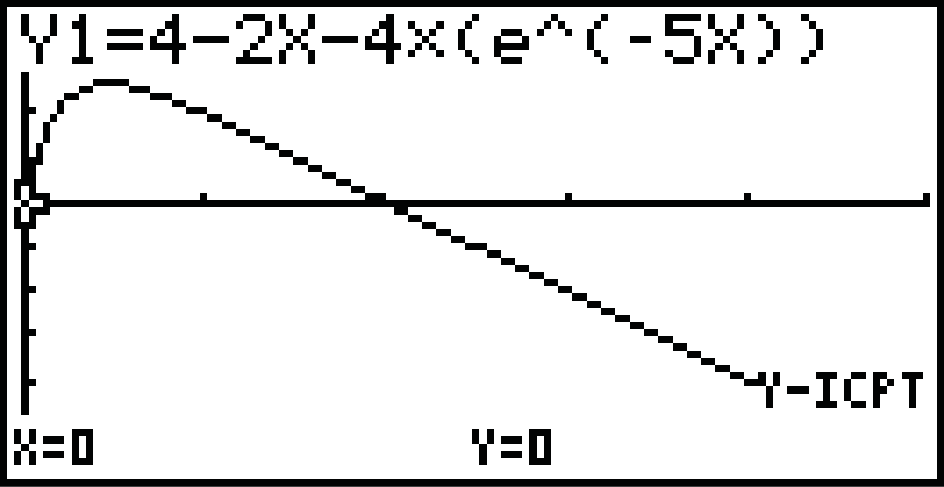
SHIFT  F5: G-Solv
F5: G-Solv  F4: Y-ICPT
F4: Y-ICPT
den Schnittpunkt mit der
(2)
- Notwendiges Kriterium:
- Hinreichendes Kriterium:
- Ableitungen
und
von der Funktion
berechnen.
- Berechne mit Hilfe des notwendigen Kriteriums die
-Koordinate.
- Prüfe das hinreichende Kriterium.
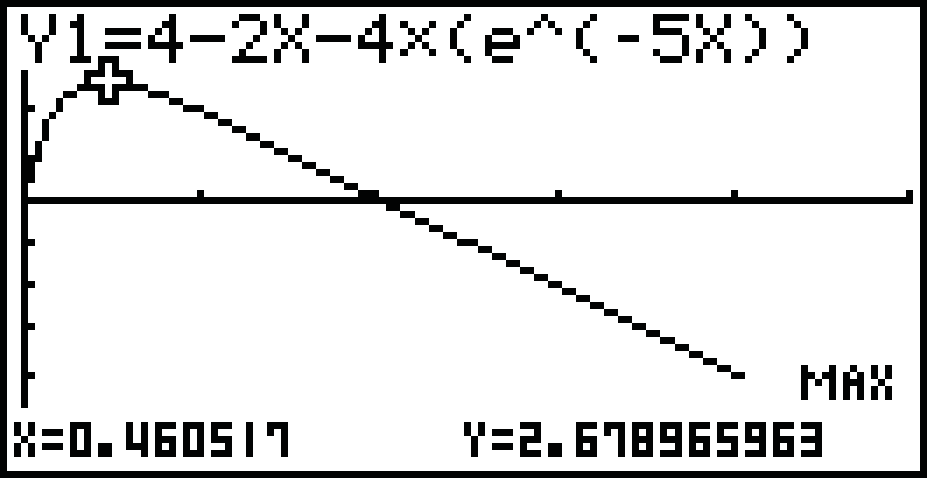
SHIFT  F5: G-Solv
F5: G-Solv  F2: MAX
F2: MAX
die Maximalstelle
b)
(1)
(2)
(3)
c)
(1)
(2)
(3)
(4)
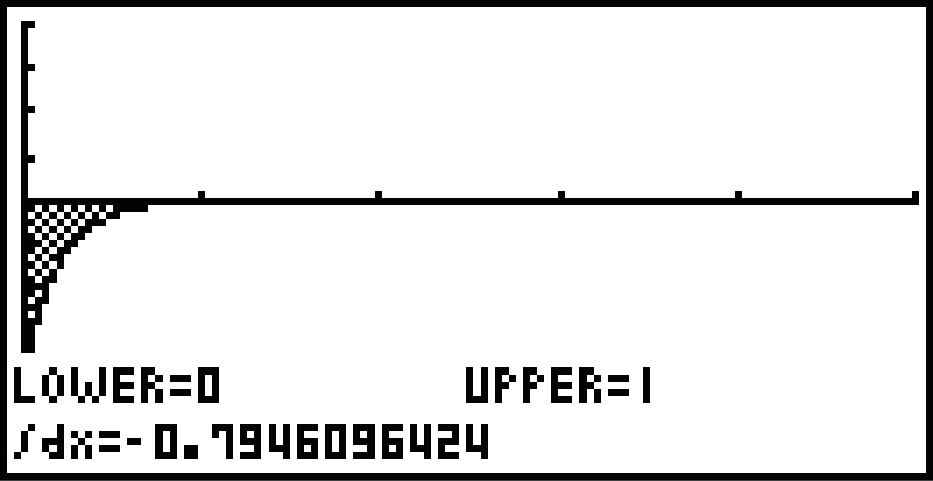
SHIFT  F5: G-Solv
F5: G-Solv  F6
F6  F3:
F3: 
den Flächeninhalt der Fläche zwischen der Geraden
d)
(1)
(2)
(3)
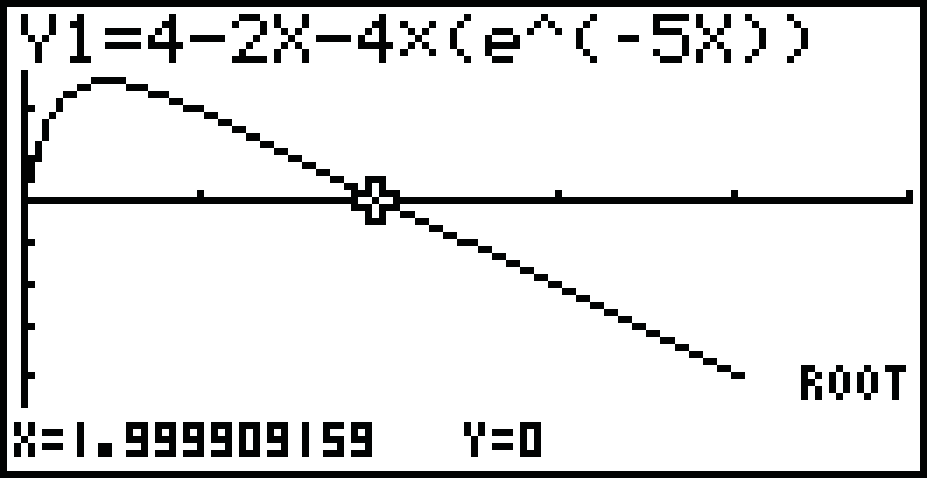
SHIFT  F5: G-Solv
F5: G-Solv  F1: ROOT.
F1: ROOT.
Hierbei kannst du mit den Pfeiltasten zwischen den einzelnen Nullstellen wechseln.
(4)
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.