B2 - Analytische Geometrie
In Rom am Piazzale Ostiense steht nach ägyptischem Vorbild die  hohe Cestius-Pyramide. Die Seitenlängen der quadratischen Grundfläche
hohe Cestius-Pyramide. Die Seitenlängen der quadratischen Grundfläche  betragen
betragen  . Die Spitze der Pyramide liegt in
. Die Spitze der Pyramide liegt in  (alle Angaben in Metern).
(alle Angaben in Metern).


Cestius-Pyramide

1.
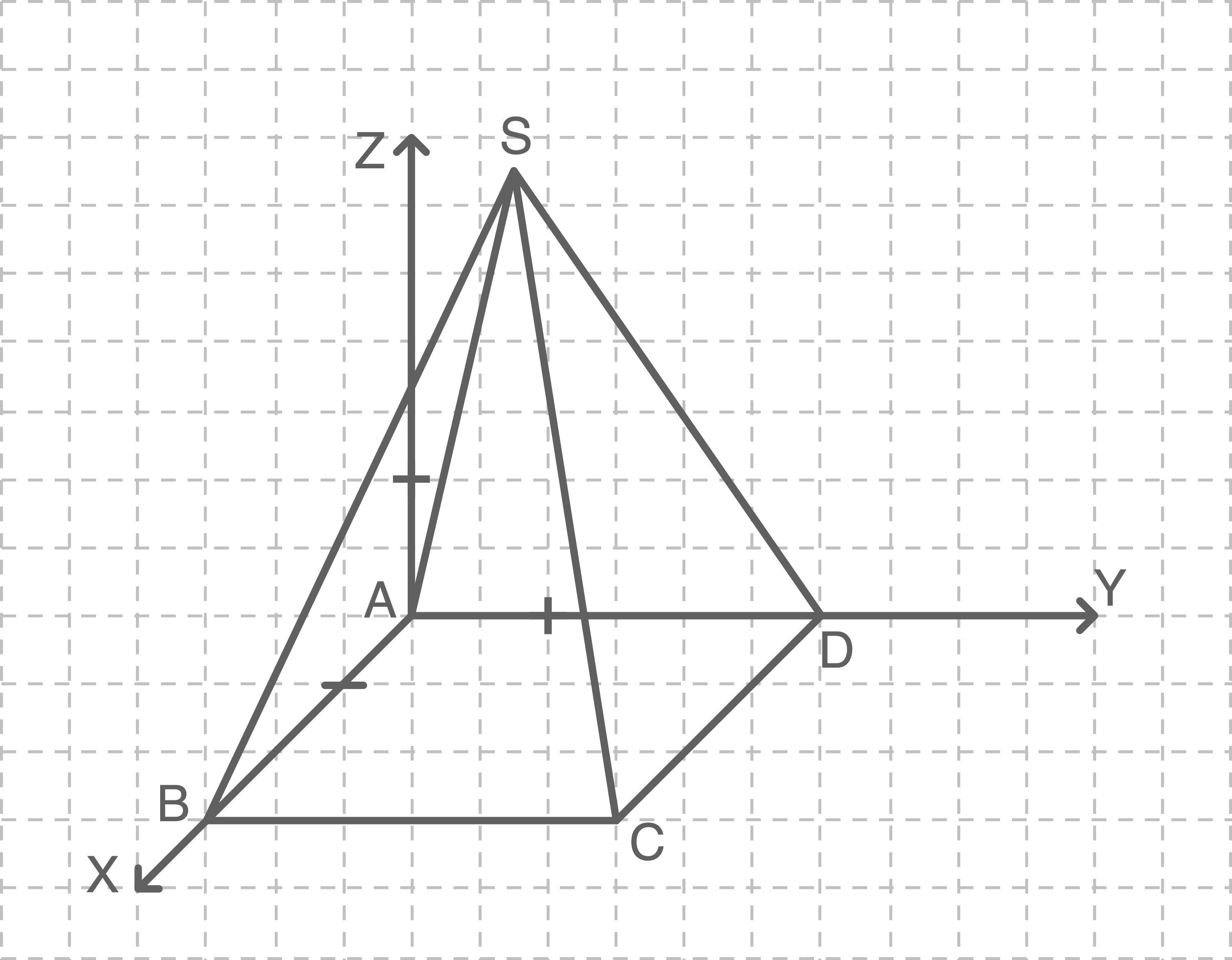
Gib die Skalierung der Achsen des Koordinatensystems aus der Aufgabenstellung und die Koordinaten der Eckpunkte  ,
,  ,
,  und
und  an.
an.
(5 BE)
2.
Ermittle eine Parametergleichung und eine Koordinatengleichung der Ebene  , in der die Pyramidenfläche
, in der die Pyramidenfläche  liegt.
liegt.
 zur Kontrolle:
zur Kontrolle:  ist eine mögliche Koordinatengleichung von
ist eine mögliche Koordinatengleichung von ![\(E.]\)](https://www.schullv.de/resources/formulas/605e41b22df8f005aaf870c850f2af37019ed22f4cd3a3f2d704fed6df0c5fa6_light.svg)
(5 BE)
3.
Zur Säuberung der teilweise mit Moos und Unkraut bewachsenen Pyramide muss ein Gebäudereiniger an den Seitenflächen hochsteigen. Bei Gebäudeflächen mit einer Neigung von mehr als  darf er diese nur mit Sicherung besteigen.
Entscheide durch eine geeignete Rechnung, ob hier eine solche Sicherung notwendig ist.
darf er diese nur mit Sicherung besteigen.
Entscheide durch eine geeignete Rechnung, ob hier eine solche Sicherung notwendig ist.
(4 BE)
4.
Die Strahlen der Vormittagssonne fallen zu einem bestimmten Zeitpunkt in Richtung des Vektors  auf die Pyramide. Eine Touristin sitzt zu diesem Zeitpunkt gegenüber der Pyramide in einem Café. Eines ihrer Augen befindet sich im Punkt
auf die Pyramide. Eine Touristin sitzt zu diesem Zeitpunkt gegenüber der Pyramide in einem Café. Eines ihrer Augen befindet sich im Punkt  .
Bestätige durch eine geeignete Rechnung, dass der Schatten der Pyramidenspitze genau in dieses Auge fällt.
.
Bestätige durch eine geeignete Rechnung, dass der Schatten der Pyramidenspitze genau in dieses Auge fällt.
(4 BE)
5.
Um die Mittagszeit fallen die Sonnenstrahlen nun in Richtung des Vektors  auf die Cestius-Pyramide. Zeige rechnerisch, dass zu diesem Zeitpunkt die Pyramide keinen Schatten spenden kann.
auf die Cestius-Pyramide. Zeige rechnerisch, dass zu diesem Zeitpunkt die Pyramide keinen Schatten spenden kann.
(6 BE)
6.
Zur Überprüfung der Stabilität des Gesteins der Pyramide wird eine Probebohrung angeordnet. Dazu wird senkrecht zur Seitenfläche  eine Bohrung bis zum Mittelpunkt der quadratischen Grundfläche durchgeführt. Berechne die Koordinaten des Punktes
eine Bohrung bis zum Mittelpunkt der quadratischen Grundfläche durchgeführt. Berechne die Koordinaten des Punktes  auf der Seitenfläche
auf der Seitenfläche  , in dem die Bohrung beginnen muss.
Bestimme die Länge des entstehenden Bohrkanals.
, in dem die Bohrung beginnen muss.
Bestimme die Länge des entstehenden Bohrkanals.
 zur Kontrolle: Auf zwei Nachkommastellen gerundet ergibt sich
zur Kontrolle: Auf zwei Nachkommastellen gerundet ergibt sich ![\(P\ (\ 15\ |\ 28,15\ |\ 4,93).]\)](https://www.schullv.de/resources/formulas/0692fda1548bfc0823b4a2e9068c0f704f7fa1d117f67abb85ac4c4b41349bd4_light.svg)
Bildnachweise [nach oben]
(6 BE)
https://commons.wikimedia.org/wiki/File:2012-07-04_Piazzale_Ostiense.jpg - Piazzale Ostiense in Rome; on the left the Pyramid of Caius Cestius, on the right Porta San Paolo, Blackcat, CC BY-SA 3.0.
1.
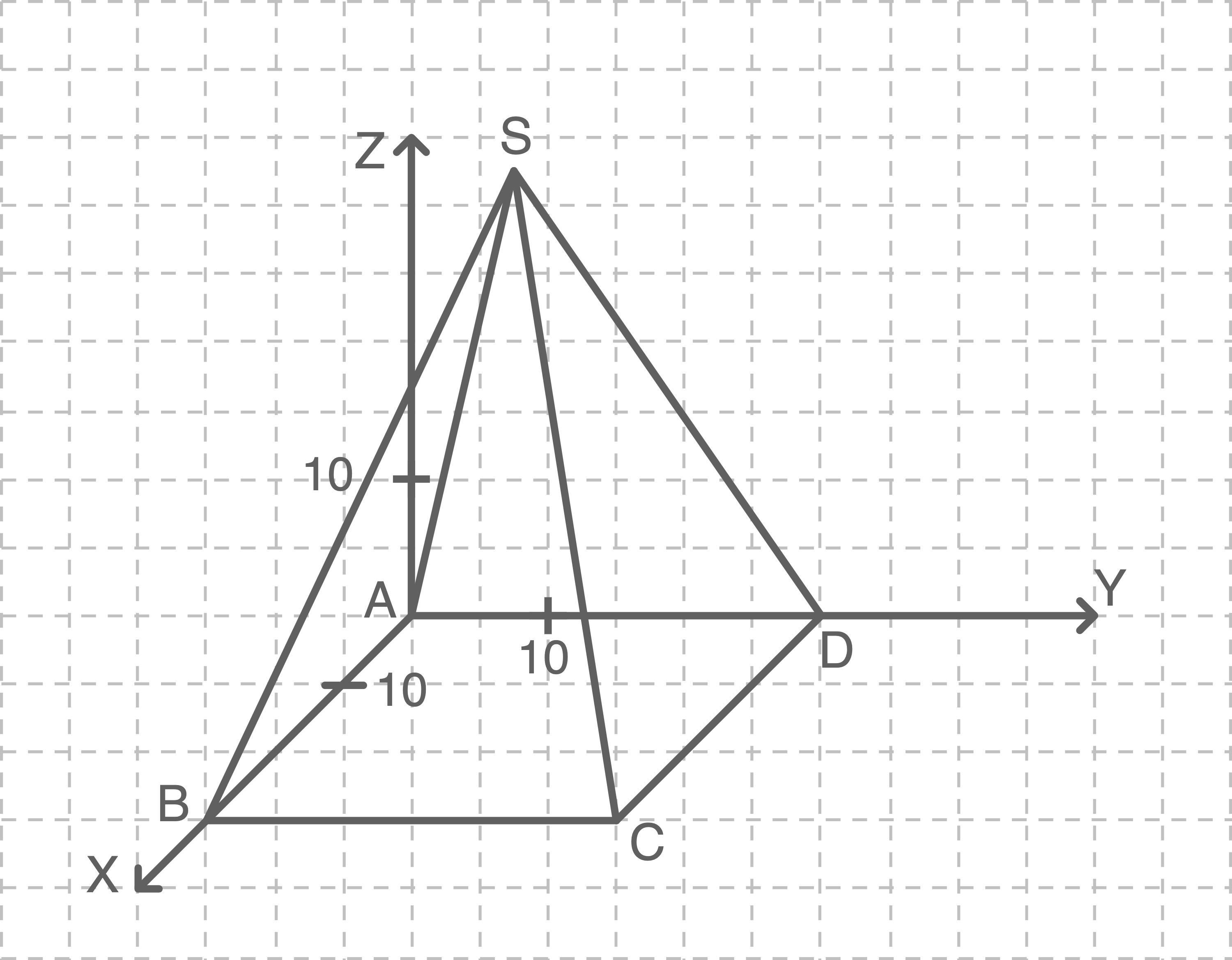
Aus der Aufgabenstellung kann entnommen werden, dass die Seitenlänge der Pyramide 30 Meter beträgt. Da die Pyramide im Koordinatensystem mit sechs Kästchen vermessen wird, entsprechen folglich jeweils zwei Kästchen 10 Metern.
Auf der  -Achse umfasst die 30 Meter lange Seite drei Kästchen, somit gibt ein Kästchen 10 Meter an.
Damit lassen sich die Koordinaten der Eckpunkte ablesen. Da sich die Eckpunkte alle in der
-Achse umfasst die 30 Meter lange Seite drei Kästchen, somit gibt ein Kästchen 10 Meter an.
Damit lassen sich die Koordinaten der Eckpunkte ablesen. Da sich die Eckpunkte alle in der  -Ebene befinden, ist die
-Ebene befinden, ist die  -Koordinate hierbei jeweils Null:
-Koordinate hierbei jeweils Null:
 ,
,  ,
,  und
und 

2.
Parametergleichung ermitteln
Für die Gleichung in Parameterform der Ebene wird der Ortsvektor eines Punktes  auf der Ebene und zwei linear unabhängige Vektoren innerhalb dieser Ebene benötigt.
Hierfür bieten sich beispielsweise der Punkt
auf der Ebene und zwei linear unabhängige Vektoren innerhalb dieser Ebene benötigt.
Hierfür bieten sich beispielsweise der Punkt  und die Verbindungsvektoren
und die Verbindungsvektoren  und
und  an:
an:



 =
= 

 =
=  Somit folgt:
Koordinatengleichung bestimmen
Einen Normalenvektor
Somit folgt:
Koordinatengleichung bestimmen
Einen Normalenvektor  ergibt sich aus dem Kreuzprodukt der Spannvektoren
ergibt sich aus dem Kreuzprodukt der Spannvektoren  und
und  der Ebene.
der Ebene.
![\(\begin{array}[t]{rll}
\overrightarrow{n}&=& \overrightarrow{DC}\times \overrightarrow{DS}& \\[5pt]
&=& \pmatrix{30\\0\\0}\times \pmatrix{15\\-15\\40}& \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/d4857e369f446f8ab7a107f18d5ba81ac5eb23db35dfd2b3d7e2f37c9c32f2b3_light.svg) Das Kreuzprodukt kann mit dem CAS berechnet werden:
Das Kreuzprodukt kann mit dem CAS berechnet werden:
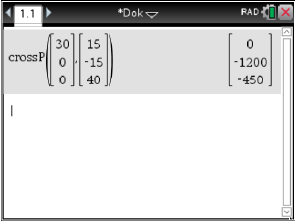 Einsetzen in die allgemeine Koordinatenform ergibt:
Einsetzen in die allgemeine Koordinatenform ergibt:
![\(\begin{array}[t]{rll}
E: \; n_1\cdot x+n_2\cdot y+n_3\cdot z&=& c& \\[5pt]
8\cdot y+3\cdot z&=& c
\end{array}\)](https://www.schullv.de/resources/formulas/2cfe067c5c4bbf61fd7b38b4df84965f07a73599bfd905732378ad1666babbfe_light.svg) Durch Einsetzen der Koordinaten eines beliebigen Punkts aus der Ebene ergibt sich:
Durch Einsetzen der Koordinaten eines beliebigen Punkts aus der Ebene ergibt sich:
![\(\begin{array}[t]{rll}
E: \; 8\cdot y+3\cdot z&=& c &\quad \scriptsize \mid\; D(0\mid 30\mid 0) \\[5pt]
8\cdot 30+3\cdot 0&=& c &\\[5pt]
240&=& c
\end{array}\)](https://www.schullv.de/resources/formulas/7c06bfe3926c0837614c49e1660c202b4903dc3fba534e60b4ba0cc5f855a132_light.svg) Eine Koordinatengleichung der Ebene
Eine Koordinatengleichung der Ebene  folgt also mit:
folgt also mit:


3.
Der Neigungswinkel der Seitenflächen entspricht dem Winkel zwischen den Normalenvektoren der Ebene der Seitenflächen und dem Normalenvektor der Grundfläche.
Ein Normalenvektor der Seitenfläche  wurde bereits in Aufgabe 2 berechnet und ist somit beispielsweise durch
wurde bereits in Aufgabe 2 berechnet und ist somit beispielsweise durch  gegeben. Aufgrund der Symmetrie der Pyramide genügt es, den Winkel einer seitenfläche zu berechnen.
Die Grundfläche entspricht der
gegeben. Aufgrund der Symmetrie der Pyramide genügt es, den Winkel einer seitenfläche zu berechnen.
Die Grundfläche entspricht der  -Ebene und besitzt somit beispielsweise den Normalenvektor
-Ebene und besitzt somit beispielsweise den Normalenvektor 
![\(\begin{array}[t]{rll}
\cos (\alpha)&=& \dfrac{\,\bigg \vert \, \overrightarrow{n_E}\circ\overrightarrow{n_{xy}}\,\bigg \vert \, }{\,\bigg \vert \,\overrightarrow{n_E}\,\bigg \vert \, \cdot \,\bigg \vert \, \overrightarrow{n_{xy}}\,\bigg \vert \, }& \\[5pt]
\cos (\alpha)&=& \dfrac{\,\left \vert \, \pmatrix{0\\8\\3}\circ\pmatrix{0\\0\\1}\,\right \vert \,}{\,\left \vert \,\pmatrix{0\\8\\3}\,\right \vert \,\cdot \,\left \vert \,\pmatrix{0\\0\\1}\,\right \vert \, }& \\[5pt]
\cos (\alpha)&=&\dfrac{\mid 0\cdot 0+8\cdot 0+3\cdot 1\mid}{\sqrt{70}\cdot \sqrt{1}} & \\[5pt]
\cos (\alpha)&=& \dfrac{3}{\sqrt{70}}&\quad \scriptsize \mid\; \arccos \\[5pt]
\alpha&\approx& 69^{\circ} & \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/c3ae45c42da7c319ad5fb3cb46a6144f1648d79a449579f968607b90097ccad4_light.svg) Der Neigungswinkel der Seitenflächen beträgt folglich etwa
Der Neigungswinkel der Seitenflächen beträgt folglich etwa  Da der Neigungswinkel somit größer als
Da der Neigungswinkel somit größer als  ist, muss der Gebäudereiniger bei seiner Arbeit gesichert werden.
ist, muss der Gebäudereiniger bei seiner Arbeit gesichert werden.
4.
1. Schritt: Geradengleichung von  aufstellen
Die Geradengleichung
aufstellen
Die Geradengleichung  gibt die Schattengerade an, welche von der Pyramidenspitze ausgeht. Trifft der Sonnenstrahl auf der Gerade die Pyramidenspitze, so liegen die nachfolgenden Punkte der Geraden im Schatten der Spitze.
gibt die Schattengerade an, welche von der Pyramidenspitze ausgeht. Trifft der Sonnenstrahl auf der Gerade die Pyramidenspitze, so liegen die nachfolgenden Punkte der Geraden im Schatten der Spitze.
![\(\begin{array}[t]{rll}
g: \; \overrightarrow{x}&=& \overrightarrow{OS} + t \cdot \overrightarrow{s_v}& \\[5pt]
&=& \begin{pmatrix}15\\15\\40\end{pmatrix} + t \cdot \begin{pmatrix}1\\2\\-4\end{pmatrix}
\end{array}\)](https://www.schullv.de/resources/formulas/17bafddc494409bd8b86a4cdb8895b971af33c33142c320b9320a056ab012c84_light.svg) 2. Schritt: Punktprobe mit Punkt
2. Schritt: Punktprobe mit Punkt  Gleichsetzen der Geradengleichung mit den Koordinaten von
Gleichsetzen der Geradengleichung mit den Koordinaten von  ergibt:
ergibt:
 Aus der ersten Zeile folgt:
Aus der ersten Zeile folgt:
![\(\begin{array}[t]{lrll}
\text{I}: & 24,75&=& 15 + 1 \cdot t & \quad \scriptsize \mid\; -15 \\[5pt]
& 9,75 &=& t
\end{array}\)](https://www.schullv.de/resources/formulas/5923715a5ac4d92539a7de8f38a38f8c1b434bfffd5ed9ba7c4c2210c9585afc_light.svg) Kontrolle durch Einsetzen von
Kontrolle durch Einsetzen von  in die zweite und dritte Zeile:
in die zweite und dritte Zeile:
![\(\begin{array}[t]{lrll}
\text{II}: & 34,5 &=& 15 + 2\cdot 9,75 & \quad \scriptsize \mid\; -15 \\[5pt]
& 34,5 &=& 34,5 &
\end{array}\)](https://www.schullv.de/resources/formulas/b4da4f9011aa0569765f5146215148cf71999d9e91ba1bd18c46104d7fec33b4_light.svg)
![\(\begin{array}[t]{lrll}
\text{III} & 1 &=& 40 - 4 \cdot t & \quad \scriptsize \mid\; -40 \\[5pt]
& - 39 &=& - 4 \cdot t & \quad \scriptsize \mid\; :(-4) \\[5pt]
& 9,75 &=& t
\end{array}\)](https://www.schullv.de/resources/formulas/3e1c5e980d2a66c9ef0d14675600e4c3a5951819fd1b5463a5082b0103229da6_light.svg) Das Gleichungssystem lässt sich mit
Das Gleichungssystem lässt sich mit  lösen, somit liegt der Punkt
lösen, somit liegt der Punkt  auf der Geraden
auf der Geraden  .
Damit fällt der Schatten der Pyramidenspitze in das Auge der Touristin.
.
Damit fällt der Schatten der Pyramidenspitze in das Auge der Touristin.
5.
Die Pyramide wirft genau dann keinen Schatten, wenn der Schattenpunkt der Pyramidenspitze innerhalb der Grundfläche der Pyramide liegt.
1. Schritt: Geradengleichung  aufstellen
Die Schattengerade der Spitze soll durch den Punkt
aufstellen
Die Schattengerade der Spitze soll durch den Punkt  und in Richtung der Sonnenstrahlen verlaufen. Somit folgt:
und in Richtung der Sonnenstrahlen verlaufen. Somit folgt:
![\(\begin{array}[t]{rll}
g_S: \overrightarrow{x}&=& \, \overrightarrow{OS} + t \cdot \overrightarrow{s_M}& \\[5pt]
&=& \begin{pmatrix}15\\15\\40\end{pmatrix} + t \cdot \begin{pmatrix}2\\1\\-20\end{pmatrix}
\end{array}\)](https://www.schullv.de/resources/formulas/f25c09b0a60bf6adf5bebd27214df644ca2f69565c18474d567e6bc7e6ab9c15_light.svg) 2. Schritt: Gleichung der
2. Schritt: Gleichung der  -Ebene bestimmen
Eine Parametergleichung der
-Ebene bestimmen
Eine Parametergleichung der  -Ebene lässt sich durch einen Punkt aus der Ebene sowie durch zwei Spannvektoren aufstellen. dabei muss die
-Ebene lässt sich durch einen Punkt aus der Ebene sowie durch zwei Spannvektoren aufstellen. dabei muss die  -Koordinate gleich null sein.
Eine mögliche Gleichung ergibt sich also beispielsweise mit:
-Koordinate gleich null sein.
Eine mögliche Gleichung ergibt sich also beispielsweise mit:
 3. Schritt: Schattenpunkt bestimmen
Gleichsetzen der Geraden- und Ebenengleichung ergibt:
3. Schritt: Schattenpunkt bestimmen
Gleichsetzen der Geraden- und Ebenengleichung ergibt:
![\(\begin{array}[t]{rll}
g_S&=& E_{xy}& \\[5pt]
\pmatrix{15\\15\\40}+t\cdot \pmatrix{2\\1\\-20}&=& \pmatrix{0\\0\\0}+s\cdot \pmatrix{1\\0\\0}+r\cdot \pmatrix{0\\1\\0}
\end{array}\)](https://www.schullv.de/resources/formulas/5dfe27300b763a1628416bb9c026be962e72e75515c3efe7359dbe25c7cc7c77_light.svg) Aus der dritten Zeile folgt
Aus der dritten Zeile folgt  und somit
und somit  Durch Einsetzen von
Durch Einsetzen von  in die erste und zweite Zeile ergeben sich
in die erste und zweite Zeile ergeben sich  und
und  als Lösungen des Gleichungssystems.
Der Schattenpunkt folgt also mit:
als Lösungen des Gleichungssystems.
Der Schattenpunkt folgt also mit:
 Da der Schattenpunkt
Da der Schattenpunkt  somit innerhalb der Grundfläche der Pyramide liegt, wirft die Pyramide zum betrachteten Zeitpunkt keinen Schatten.
somit innerhalb der Grundfläche der Pyramide liegt, wirft die Pyramide zum betrachteten Zeitpunkt keinen Schatten.
6.
1.Schritt: Geradengleichung des Bohrkanals bestimmen
Da der Borhkanal auf den Mittelpunkt der quadratischen Grundfläche treffen soll, muss dieser auf der Geraden liegen. Der Mittelpunkt  dient somit als Stützvektor der Geraden.
Als Richtungsvektor bietet sich ein Normalenvektor der Ebene
dient somit als Stützvektor der Geraden.
Als Richtungsvektor bietet sich ein Normalenvektor der Ebene  an. In Aufgabe 2 wurde hierfür bereits beispielsweise der Normalenvektor
an. In Aufgabe 2 wurde hierfür bereits beispielsweise der Normalenvektor  ermittelt.
Es folgt also:
ermittelt.
Es folgt also:
![\(\begin{array}[t]{rll}
g_B&=& \overrightarrow{OM} +s \cdot \overrightarrow{n} & \\[5pt]
&=&\pmatrix{15\\15\\0}+s\cdot \pmatrix{0\\8\\3} & \\[5pt]
&=&\pmatrix{15\\15+8s\\3s} & \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/135b6358a37411b8091653ba490398a0f9a44c7feab44cd06d10cbce6e3b6eda_light.svg) 2.Schritt: Lotfußpunkt bestimmen
Die Koordinatengleichung der Ebene
2.Schritt: Lotfußpunkt bestimmen
Die Koordinatengleichung der Ebene  wurde bereits in Aufgabe 2 bestimmt:
wurde bereits in Aufgabe 2 bestimmt:
 Geradengleichung
Geradengleichung  einsetzen:
einsetzen:
![\(\begin{array}[t]{rll}
8 \cdot (15 +8 s) + 3 \cdot 3s &=& 240 & \\[5pt]
120+64s+9s &=& 240 \quad \scriptsize \mid\; -120 \\[5pt]
73s &=& 120 \quad \scriptsize \mid\; :73 \\[5pt]
s &=& \dfrac{120}{73} \quad \scriptsize \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/b351647a908c1f97684d2618a74bd20cad00517c1d581421a17ee357fdc46195_light.svg) Einsetzen von
Einsetzen von  in die Geradengleichung liefert die Koordinaten des gesuchten Punkts:
in die Geradengleichung liefert die Koordinaten des gesuchten Punkts:
![\(\begin{array}[t]{rll}
g_B&=& \pmatrix{15\\15\\0}+\dfrac{120}{73} \cdot \pmatrix{0\\8\\3}& \\[5pt]
&\approx& \pmatrix{15\\28,15\\4,93}
\end{array}\)](https://www.schullv.de/resources/formulas/a34550f777481856cf0ce48111b3109014a50e191afb81c049083d4b328de782_light.svg) Somit muss die Bohrung im Punkt
Somit muss die Bohrung im Punkt  beginnen.
Länge des Bohrkanls bestimmen
Mit den Koordinaten des Mittelpunkts
beginnen.
Länge des Bohrkanls bestimmen
Mit den Koordinaten des Mittelpunkts  und des Bohrpunkts
und des Bohrpunkts  kann der Abstand wie folgt ermittelt werden:
kann der Abstand wie folgt ermittelt werden:
![\(\begin{array}[t]{rll}
l&=&\sqrt{(x_m-x_p)^2+(y_m-y_p)^2+(z_m-z_p)^2} &\\[5pt]
&=& \sqrt{(15-15)^2+(15-28,15)^2+(0-4,93)^2} &\\[5pt]
&=& \sqrt{0+(-13,15)^2+(-4,93)^2}&\\[5pt]
&=& \sqrt{197,2274} &\\[5pt]
&\approx & 14,04 \; [\,\text{m}]
\end{array}\)](https://www.schullv.de/resources/formulas/8c6eb8ab9f9d3f6f3d55382834df75d9b056b6b15aab3047c8c2cb8a3526d977_light.svg) Alternativ kann die Länge des Bohrkanals auch mit dem CAS bestimmt werden.
Alternativ kann die Länge des Bohrkanals auch mit dem CAS bestimmt werden.
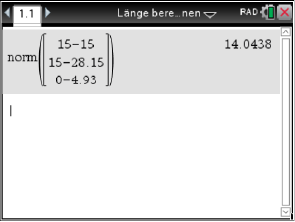 Die Länge des Bohrkanals beträgt folglich etwa 14,04 Meter.
Die Länge des Bohrkanals beträgt folglich etwa 14,04 Meter.

1.
Aus der Aufgabenstellung kann entnommen werden, dass die Seitenlänge der Pyramide 30 Meter beträgt. Da die Pyramide im Koordinatensystem mit sechs Kästchen vermessen wird, entsprechen folglich jeweils zwei Kästchen 10 Metern.
Auf der  -Achse umfasst die 30 Meter lange Seite drei Kästchen, somit gibt ein Kästchen 10 Meter an.
Damit lassen sich die Koordinaten der Eckpunkte ablesen. Da sich die Eckpunkte alle in der
-Achse umfasst die 30 Meter lange Seite drei Kästchen, somit gibt ein Kästchen 10 Meter an.
Damit lassen sich die Koordinaten der Eckpunkte ablesen. Da sich die Eckpunkte alle in der  -Ebene befinden, ist die
-Ebene befinden, ist die  -Koordinate hierbei jeweils Null:
-Koordinate hierbei jeweils Null:
 ,
,  ,
,  und
und 


2.
Parametergleichung ermitteln
Für die Gleichung in Parameterform der Ebene wird der Ortsvektor eines Punktes  auf der Ebene und zwei linear unabhängige Vektoren innerhalb dieser Ebene benötigt.
Hierfür bieten sich beispielsweise der Punkt
auf der Ebene und zwei linear unabhängige Vektoren innerhalb dieser Ebene benötigt.
Hierfür bieten sich beispielsweise der Punkt  und die Verbindungsvektoren
und die Verbindungsvektoren  und
und  an:
an:



 =
= 

 =
=  Somit folgt:
Koordinatengleichung bestimmen
Einen Normalenvektor
Somit folgt:
Koordinatengleichung bestimmen
Einen Normalenvektor  ergibt sich aus dem Kreuzprodukt der Spannvektoren
ergibt sich aus dem Kreuzprodukt der Spannvektoren  und
und  der Ebene.
der Ebene.
![\(\begin{array}[t]{rll}
\overrightarrow{n}&=& \overrightarrow{DC}\times \overrightarrow{DS}& \\[5pt]
&=& \pmatrix{30\\0\\0}\times \pmatrix{15\\-15\\40}& \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/d4857e369f446f8ab7a107f18d5ba81ac5eb23db35dfd2b3d7e2f37c9c32f2b3_light.svg) Das Kreuzprodukt kann mit dem CAS berechnet werden:
Das Kreuzprodukt kann mit dem CAS berechnet werden:
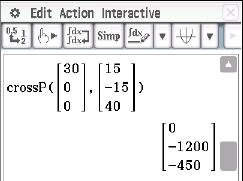 Einsetzen in die allgemeine Koordinatenform ergibt:
Einsetzen in die allgemeine Koordinatenform ergibt:
![\(\begin{array}[t]{rll}
E: \; n_1\cdot x+n_2\cdot y+n_3\cdot z&=& c& \\[5pt]
8\cdot y+3\cdot z&=& c
\end{array}\)](https://www.schullv.de/resources/formulas/2cfe067c5c4bbf61fd7b38b4df84965f07a73599bfd905732378ad1666babbfe_light.svg) Durch Einsetzen der Koordinaten eines beliebigen Punkts aus der Ebene ergibt sich:
Durch Einsetzen der Koordinaten eines beliebigen Punkts aus der Ebene ergibt sich:
![\(\begin{array}[t]{rll}
E: \; 8\cdot y+3\cdot z&=& c &\quad \scriptsize \mid\; D(0\mid 30\mid 0) \\[5pt]
8\cdot 30+3\cdot 0&=& c &\\[5pt]
240&=& c
\end{array}\)](https://www.schullv.de/resources/formulas/7c06bfe3926c0837614c49e1660c202b4903dc3fba534e60b4ba0cc5f855a132_light.svg) Eine Koordinatengleichung der Ebene
Eine Koordinatengleichung der Ebene  folgt also mit:
folgt also mit:


3.
Der Neigungswinkel der Seitenflächen entspricht dem Winkel zwischen den Normalenvektoren der Ebene der Seitenflächen und dem Normalenvektor der Grundfläche.
Ein Normalenvektor der Seitenfläche  wurde bereits in Aufgabe 2 berechnet und ist somit beispielsweise durch
wurde bereits in Aufgabe 2 berechnet und ist somit beispielsweise durch  gegeben. Aufgrund der Symmetrie der Pyramide genügt es, den Winkel einer seitenfläche zu berechnen.
Die Grundfläche entspricht der
gegeben. Aufgrund der Symmetrie der Pyramide genügt es, den Winkel einer seitenfläche zu berechnen.
Die Grundfläche entspricht der  -Ebene und besitzt somit beispielsweise den Normalenvektor
-Ebene und besitzt somit beispielsweise den Normalenvektor 
![\(\begin{array}[t]{rll}
\cos (\alpha)&=& \dfrac{\,\bigg \vert \, \overrightarrow{n_E}\circ\overrightarrow{n_{xy}}\,\bigg \vert \, }{\,\bigg \vert \,\overrightarrow{n_E}\,\bigg \vert \, \cdot \,\bigg \vert \, \overrightarrow{n_{xy}}\,\bigg \vert \, }& \\[5pt]
\cos (\alpha)&=& \dfrac{\,\left \vert \, \pmatrix{0\\8\\3}\circ\pmatrix{0\\0\\1}\,\right \vert \,}{\,\left \vert \,\pmatrix{0\\8\\3}\,\right \vert \,\cdot \,\left \vert \,\pmatrix{0\\0\\1}\,\right \vert \, }& \\[5pt]
\cos (\alpha)&=&\dfrac{\mid 0\cdot 0+8\cdot 0+3\cdot 1\mid}{\sqrt{70}\cdot \sqrt{1}} & \\[5pt]
\cos (\alpha)&=& \dfrac{3}{\sqrt{70}}&\quad \scriptsize \mid\; \arccos \\[5pt]
\alpha&\approx& 69^{\circ} & \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/c3ae45c42da7c319ad5fb3cb46a6144f1648d79a449579f968607b90097ccad4_light.svg) Der Neigungswinkel der Seitenflächen beträgt folglich etwa
Der Neigungswinkel der Seitenflächen beträgt folglich etwa  Da der Neigungswinkel somit größer als
Da der Neigungswinkel somit größer als  ist, muss der Gebäudereiniger bei seiner Arbeit gesichert werden.
ist, muss der Gebäudereiniger bei seiner Arbeit gesichert werden.
4.
1. Schritt: Geradengleichung von  aufstellen
Die Geradengleichung
aufstellen
Die Geradengleichung  gibt die Schattengerade an, welche von der Pyramidenspitze ausgeht. Trifft der Sonnenstrahl auf der Gerade die Pyramidenspitze, so liegen die nachfolgenden Punkte der Geraden im Schatten der Spitze.
gibt die Schattengerade an, welche von der Pyramidenspitze ausgeht. Trifft der Sonnenstrahl auf der Gerade die Pyramidenspitze, so liegen die nachfolgenden Punkte der Geraden im Schatten der Spitze.
![\(\begin{array}[t]{rll}
g: \; \overrightarrow{x}&=& \overrightarrow{OS} + t \cdot \overrightarrow{s_v}& \\[5pt]
&=& \begin{pmatrix}15\\15\\40\end{pmatrix} + t \cdot \begin{pmatrix}1\\2\\-4\end{pmatrix}
\end{array}\)](https://www.schullv.de/resources/formulas/17bafddc494409bd8b86a4cdb8895b971af33c33142c320b9320a056ab012c84_light.svg) 2. Schritt: Punktprobe mit Punkt
2. Schritt: Punktprobe mit Punkt  Gleichsetzen der Geradengleichung mit den Koordinaten von
Gleichsetzen der Geradengleichung mit den Koordinaten von  ergibt:
ergibt:
 Aus der ersten Zeile folgt:
Aus der ersten Zeile folgt:
![\(\begin{array}[t]{lrll}
\text{I}: & 24,75&=& 15 + 1 \cdot t & \quad \scriptsize \mid\; -15 \\[5pt]
& 9,75 &=& t
\end{array}\)](https://www.schullv.de/resources/formulas/5923715a5ac4d92539a7de8f38a38f8c1b434bfffd5ed9ba7c4c2210c9585afc_light.svg) Kontrolle durch Einsetzen von
Kontrolle durch Einsetzen von  in die zweite und dritte Zeile:
in die zweite und dritte Zeile:
![\(\begin{array}[t]{lrll}
\text{II}: & 34,5 &=& 15 + 2\cdot 9,75 & \quad \scriptsize \mid\; -15 \\[5pt]
& 34,5 &=& 34,5 &
\end{array}\)](https://www.schullv.de/resources/formulas/b4da4f9011aa0569765f5146215148cf71999d9e91ba1bd18c46104d7fec33b4_light.svg)
![\(\begin{array}[t]{lrll}
\text{III} & 1 &=& 40 - 4 \cdot t & \quad \scriptsize \mid\; -40 \\[5pt]
& - 39 &=& - 4 \cdot t & \quad \scriptsize \mid\; :(-4) \\[5pt]
& 9,75 &=& t
\end{array}\)](https://www.schullv.de/resources/formulas/3e1c5e980d2a66c9ef0d14675600e4c3a5951819fd1b5463a5082b0103229da6_light.svg) Das Gleichungssystem lässt sich mit
Das Gleichungssystem lässt sich mit  lösen, somit liegt der Punkt
lösen, somit liegt der Punkt  auf der Geraden
auf der Geraden  .
Damit fällt der Schatten der Pyramidenspitze in das Auge der Touristin.
.
Damit fällt der Schatten der Pyramidenspitze in das Auge der Touristin.
5.
Die Pyramide wirft genau dann keinen Schatten, wenn der Schattenpunkt der Pyramidenspitze innerhalb der Grundfläche der Pyramide liegt.
1. Schritt: Geradengleichung  aufstellen
Die Schattengerade der Spitze soll durch den Punkt
aufstellen
Die Schattengerade der Spitze soll durch den Punkt  und in Richtung der Sonnenstrahlen verlaufen. Somit folgt:
und in Richtung der Sonnenstrahlen verlaufen. Somit folgt:
![\(\begin{array}[t]{rll}
g_S: \overrightarrow{x}&=& \, \overrightarrow{OS} + t \cdot \overrightarrow{s_M}& \\[5pt]
&=& \begin{pmatrix}15\\15\\40\end{pmatrix} + t \cdot \begin{pmatrix}2\\1\\-20\end{pmatrix}
\end{array}\)](https://www.schullv.de/resources/formulas/f25c09b0a60bf6adf5bebd27214df644ca2f69565c18474d567e6bc7e6ab9c15_light.svg) 2. Schritt: Gleichung der
2. Schritt: Gleichung der  -Ebene bestimmen
Eine Parametergleichung der
-Ebene bestimmen
Eine Parametergleichung der  -Ebene lässt sich durch einen Punkt aus der Ebene sowie durch zwei Spannvektoren aufstellen. dabei muss die
-Ebene lässt sich durch einen Punkt aus der Ebene sowie durch zwei Spannvektoren aufstellen. dabei muss die  -Koordinate gleich null sein.
Eine mögliche Gleichung ergibt sich also beispielsweise mit:
-Koordinate gleich null sein.
Eine mögliche Gleichung ergibt sich also beispielsweise mit:
 3. Schritt: Schattenpunkt bestimmen
Gleichsetzen der Geraden- und Ebenengleichung ergibt:
3. Schritt: Schattenpunkt bestimmen
Gleichsetzen der Geraden- und Ebenengleichung ergibt:
![\(\begin{array}[t]{rll}
g_S&=& E_{xy}& \\[5pt]
\pmatrix{15\\15\\40}+t\cdot \pmatrix{2\\1\\-20}&=& \pmatrix{0\\0\\0}+s\cdot \pmatrix{1\\0\\0}+r\cdot \pmatrix{0\\1\\0}
\end{array}\)](https://www.schullv.de/resources/formulas/5dfe27300b763a1628416bb9c026be962e72e75515c3efe7359dbe25c7cc7c77_light.svg) Aus der dritten Zeile folgt
Aus der dritten Zeile folgt  und somit
und somit  Durch Einsetzen von
Durch Einsetzen von  in die erste und zweite Zeile ergeben sich
in die erste und zweite Zeile ergeben sich  und
und  als Lösungen des Gleichungssystems.
Der Schattenpunkt folgt also mit:
als Lösungen des Gleichungssystems.
Der Schattenpunkt folgt also mit:
 Da der Schattenpunkt
Da der Schattenpunkt  somit innerhalb der Grundfläche der Pyramide liegt, wirft die Pyramide zum betrachteten Zeitpunkt keinen Schatten.
somit innerhalb der Grundfläche der Pyramide liegt, wirft die Pyramide zum betrachteten Zeitpunkt keinen Schatten.
6.
1.Schritt: Geradengleichung des Bohrkanals bestimmen
Da der Borhkanal auf den Mittelpunkt der quadratischen Grundfläche treffen soll, muss dieser auf der Geraden liegen. Der Mittelpunkt  dient somit als Stützvektor der Geraden.
Als Richtungsvektor bietet sich ein Normalenvektor der Ebene
dient somit als Stützvektor der Geraden.
Als Richtungsvektor bietet sich ein Normalenvektor der Ebene  an. In Aufgabe 2 wurde hierfür bereits beispielsweise der Normalenvektor
an. In Aufgabe 2 wurde hierfür bereits beispielsweise der Normalenvektor  ermittelt.
Es folgt also:
ermittelt.
Es folgt also:
![\(\begin{array}[t]{rll}
g_B&=& \overrightarrow{OM} +s \cdot \overrightarrow{n} & \\[5pt]
&=&\pmatrix{15\\15\\0}+s\cdot \pmatrix{0\\8\\3} & \\[5pt]
&=&\pmatrix{15\\15+8s\\3s} & \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/135b6358a37411b8091653ba490398a0f9a44c7feab44cd06d10cbce6e3b6eda_light.svg) 2.Schritt: Lotfußpunkt bestimmen
Die Koordinatengleichung der Ebene
2.Schritt: Lotfußpunkt bestimmen
Die Koordinatengleichung der Ebene  wurde bereits in Aufgabe 2 bestimmt:
wurde bereits in Aufgabe 2 bestimmt:
 Geradengleichung
Geradengleichung  einsetzen:
einsetzen:
![\(\begin{array}[t]{rll}
8 \cdot (15 +8 s) + 3 \cdot 3s &=& 240 & \\[5pt]
120+64s+9s &=& 240 \quad \scriptsize \mid\; -120 \\[5pt]
73s &=& 120 \quad \scriptsize \mid\; :73 \\[5pt]
s &=& \dfrac{120}{73} \quad \scriptsize \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/b351647a908c1f97684d2618a74bd20cad00517c1d581421a17ee357fdc46195_light.svg) Einsetzen von
Einsetzen von  in die Geradengleichung liefert die Koordinaten des gesuchten Punkts:
in die Geradengleichung liefert die Koordinaten des gesuchten Punkts:
![\(\begin{array}[t]{rll}
g_B&=& \pmatrix{15\\15\\0}+\dfrac{120}{73} \cdot \pmatrix{0\\8\\3}& \\[5pt]
&\approx& \pmatrix{15\\28,15\\4,93}
\end{array}\)](https://www.schullv.de/resources/formulas/a34550f777481856cf0ce48111b3109014a50e191afb81c049083d4b328de782_light.svg) Somit muss die Bohrung im Punkt
Somit muss die Bohrung im Punkt  beginnen.
Länge des Bohrkanls bestimmen
Mit den Koordinaten des Mittelpunkts
beginnen.
Länge des Bohrkanls bestimmen
Mit den Koordinaten des Mittelpunkts  und des Bohrpunkts
und des Bohrpunkts  kann der Abstand wie folgt ermittelt werden:
kann der Abstand wie folgt ermittelt werden:
![\(\begin{array}[t]{rll}
l&=&\sqrt{(x_m-x_p)^2+(y_m-y_p)^2+(z_m-z_p)^2} &\\[5pt]
&=& \sqrt{(15-15)^2+(15-28,15)^2+(0-4,93)^2} &\\[5pt]
&=& \sqrt{0+(-13,15)^2+(-4,93)^2}&\\[5pt]
&=& \sqrt{197,2274} &\\[5pt]
&\approx & 14,04 \; [\,\text{m}]
\end{array}\)](https://www.schullv.de/resources/formulas/8c6eb8ab9f9d3f6f3d55382834df75d9b056b6b15aab3047c8c2cb8a3526d977_light.svg) Die Länge des Bohrkanals beträgt folglich etwa 14,04 Meter.
Die Länge des Bohrkanals beträgt folglich etwa 14,04 Meter.