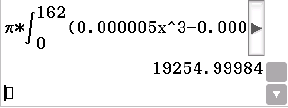A2 - Analysis
Der Kühlturm des Kernkraftwerkes Mülheim-Kärlich soll vom Betreiber abgerissen werden. Deshalb ist eine Abschätzung des anfallenden Bauschutts erforderlich. Der Kühlturm hat eine Höhe von  und ist aus Stahlbeton gebaut.
und ist aus Stahlbeton gebaut.  des verwendeten Stahlbetons hat eine Masse von
des verwendeten Stahlbetons hat eine Masse von  .
Für die folgende Untersuchung soll die waagrecht gemessene Wandstärke des Kühlturms mit
.
Für die folgende Untersuchung soll die waagrecht gemessene Wandstärke des Kühlturms mit  als konstant angenommen werden.
Zur Modellierung betrachten wir den um
als konstant angenommen werden.
Zur Modellierung betrachten wir den um  ° nach rechts gedrehten Kühlturm. Die äußere Randfunktion kann bei dieser Modellierung näherungsweise durch verschiedene ganzrationale Funktionen dargestellt werden. Durch Rotation des Graphen der äußeren Randfunktion um die
° nach rechts gedrehten Kühlturm. Die äußere Randfunktion kann bei dieser Modellierung näherungsweise durch verschiedene ganzrationale Funktionen dargestellt werden. Durch Rotation des Graphen der äußeren Randfunktion um die  -Achse erhält man die Form des Kühlturms.
-Achse erhält man die Form des Kühlturms.

Abb. 1
1.
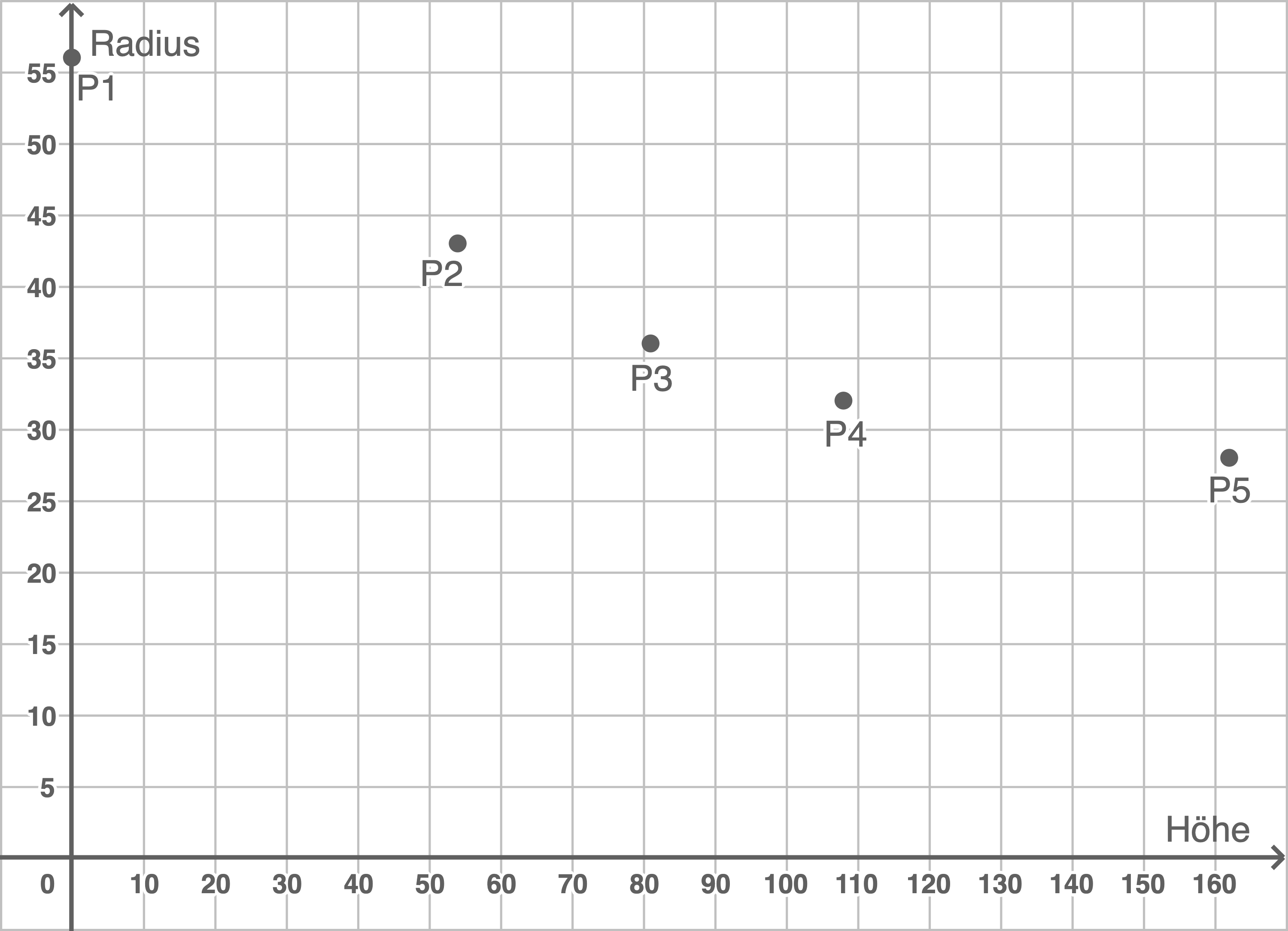
Zeichne die Stützpunkte der Randfunktion der Variante C in das folgende Koordinatensystem:
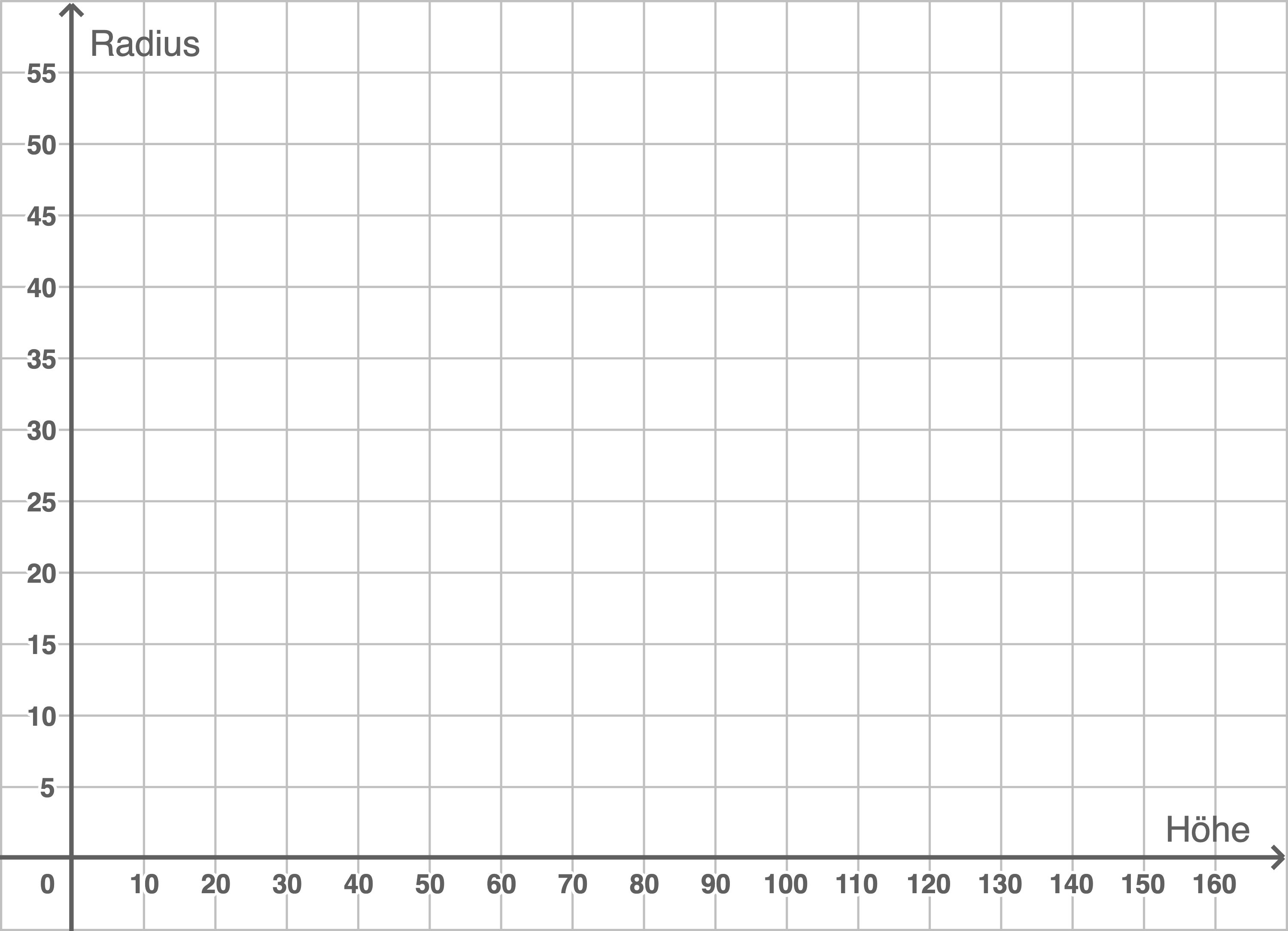
(2 BE)

2.
Bestimme geeignete ganzrationale Funktionen  und
und  für die in der Tabelle dargestellten Varianten A und B und begründe deinen Ansatz.
Skizziere die Graphen von
für die in der Tabelle dargestellten Varianten A und B und begründe deinen Ansatz.
Skizziere die Graphen von  und
und  in das Koordinatensystem aus Aufgabe 1 und vergleiche die Qualität der Annäherung beider Funktionen unter Berücksichtigung aller fünf Stützpunkte.
in das Koordinatensystem aus Aufgabe 1 und vergleiche die Qualität der Annäherung beider Funktionen unter Berücksichtigung aller fünf Stützpunkte.
(12 BE)
3.
3.1
Bestimme unter Verwendung aller angegebenen Stützpunkte näherungsweise eine ganzrationale Randfunktion 3. Grades  für die in der Tabelle dargestellte Variante C.
für die in der Tabelle dargestellte Variante C.
(6 BE)
3.2
Bestimme unter Verwendung der Funktion  aus Aufgabenteil 3.1 den minimalen Umfang des Kühlturmes.
Hinweis: Falls
aus Aufgabenteil 3.1 den minimalen Umfang des Kühlturmes.
Hinweis: Falls  nicht bestimmt werden konnte, kann stattdessen die folgende Funktion
nicht bestimmt werden konnte, kann stattdessen die folgende Funktion  verwendet werden:
verwendet werden:
(6 BE)
4.
Um die ermittelte Randfunktion  aus Aufgabenteil 3.1 genauer zu untersuchen, wird der folgende Term berechnet:
Erläutere diese Rechnung.
Ermittle, welches Ergebnis man erhält, wenn man in der obigen Rechnung die Randfunktion
aus Aufgabenteil 3.1 genauer zu untersuchen, wird der folgende Term berechnet:
Erläutere diese Rechnung.
Ermittle, welches Ergebnis man erhält, wenn man in der obigen Rechnung die Randfunktion  durch die Randfunktion
durch die Randfunktion  aus Aufgabe 2 ersetzt, und deute die beiden Ergebnisse im Sachzusammenhang.
Hinweis: Falls
aus Aufgabe 2 ersetzt, und deute die beiden Ergebnisse im Sachzusammenhang.
Hinweis: Falls  nicht bestimmt werden konnte, kann stattdessen die Funktion
nicht bestimmt werden konnte, kann stattdessen die Funktion  mit
mit  verwendet werden.
verwendet werden.
(7 BE)
5.
Bestimme zu  eine innere Randfunktion
eine innere Randfunktion  , wenn die Wandstärke des Kühlturms wie oben beschrieben
, wenn die Wandstärke des Kühlturms wie oben beschrieben  beträgt. Ermittle damit Volumen und Masse des Bauschutts, der bei Abriss der Kühlturmwand entsteht.
Hinweis: Falls
beträgt. Ermittle damit Volumen und Masse des Bauschutts, der bei Abriss der Kühlturmwand entsteht.
Hinweis: Falls  nicht bestimmt werden konnte, kann stattdessen die Funktion
nicht bestimmt werden konnte, kann stattdessen die Funktion  aus Aufgabenteil 3.2 verwendet werden.
aus Aufgabenteil 3.2 verwendet werden.
Bildnachweise
Abb.1: https://de.wikipedia.org/wiki/Kernkraftwerk_Mülheim-Kärlich
(7 BE)
1.
2.
Funktion  bestimmen
Da drei Stützpunkte gegeben sind, handelt es sich hierbei um eine quadratische Funktionsgleichung. Eine Funktion höheren Grades würde mehr als drei Stützpunkte benötigen.
Allgemeine quadratische Funktion:
bestimmen
Da drei Stützpunkte gegeben sind, handelt es sich hierbei um eine quadratische Funktionsgleichung. Eine Funktion höheren Grades würde mehr als drei Stützpunkte benötigen.
Allgemeine quadratische Funktion:  Anhand der in der Aufgabenstellung gegebenen Stützpunkte kann nun ein lineares Gleichungssystem aufgestellt werden:
Anhand der in der Aufgabenstellung gegebenen Stützpunkte kann nun ein lineares Gleichungssystem aufgestellt werden:
![\(\begin{array}[t]{rll}
f_A(0)&=& 56 \\[5pt]
f_A(81)&=& 36 \\[5pt]
f_A(162)&=& 28 \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/2851b5fd4b16fb733b7374596de4f633c36836d8ec0f86617dc9a5ff7b7e78ff_light.svg) Gleichungssystem aufstellen:
Gleichungssystem aufstellen:
 Mit dem solve-Befehl des CAS ergibt sich:
Mit dem solve-Befehl des CAS ergibt sich:
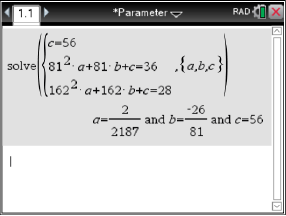 Es folgen somit
Es folgen somit 
 und
und  Die Funktionsgleichung von
Die Funktionsgleichung von  folgt also mit:
folgt also mit:
 Funktion
Funktion  bestimmen
Analog zur Funktion
bestimmen
Analog zur Funktion  folgt:
folgt:
![\(\begin{array}[t]{rll}
f_B(0)&=& 56 \\[5pt]
f_B(54)&=& 43 \\[5pt]
f_B(162)&=& 28 \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/5eb3aed9ab4d718fc2f348f03e496bc331be4676ac7bfcfe474b6c21dc7c80b8_light.svg) Gleichungssystem aufstellen:
Gleichungssystem aufstellen:
 Mit dem CAS ergibt sich:
Mit dem CAS ergibt sich:
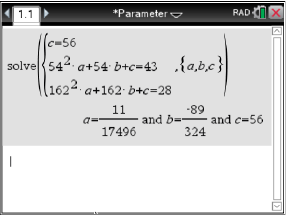 Es folgen somit
Es folgen somit 
 und
und  Die Funktionsgleichung von
Die Funktionsgleichung von  folgt also mit:
folgt also mit:
 Graphen skizzieren
Die Funktionen können mit dem CAS angezeigt werden. Durch Erstellen von Wertetabellen mit dem CAS lassen sich außerdem Punkte bestimmen, anhand derer der Graph skizziert werden kann.
Graphen skizzieren
Die Funktionen können mit dem CAS angezeigt werden. Durch Erstellen von Wertetabellen mit dem CAS lassen sich außerdem Punkte bestimmen, anhand derer der Graph skizziert werden kann.
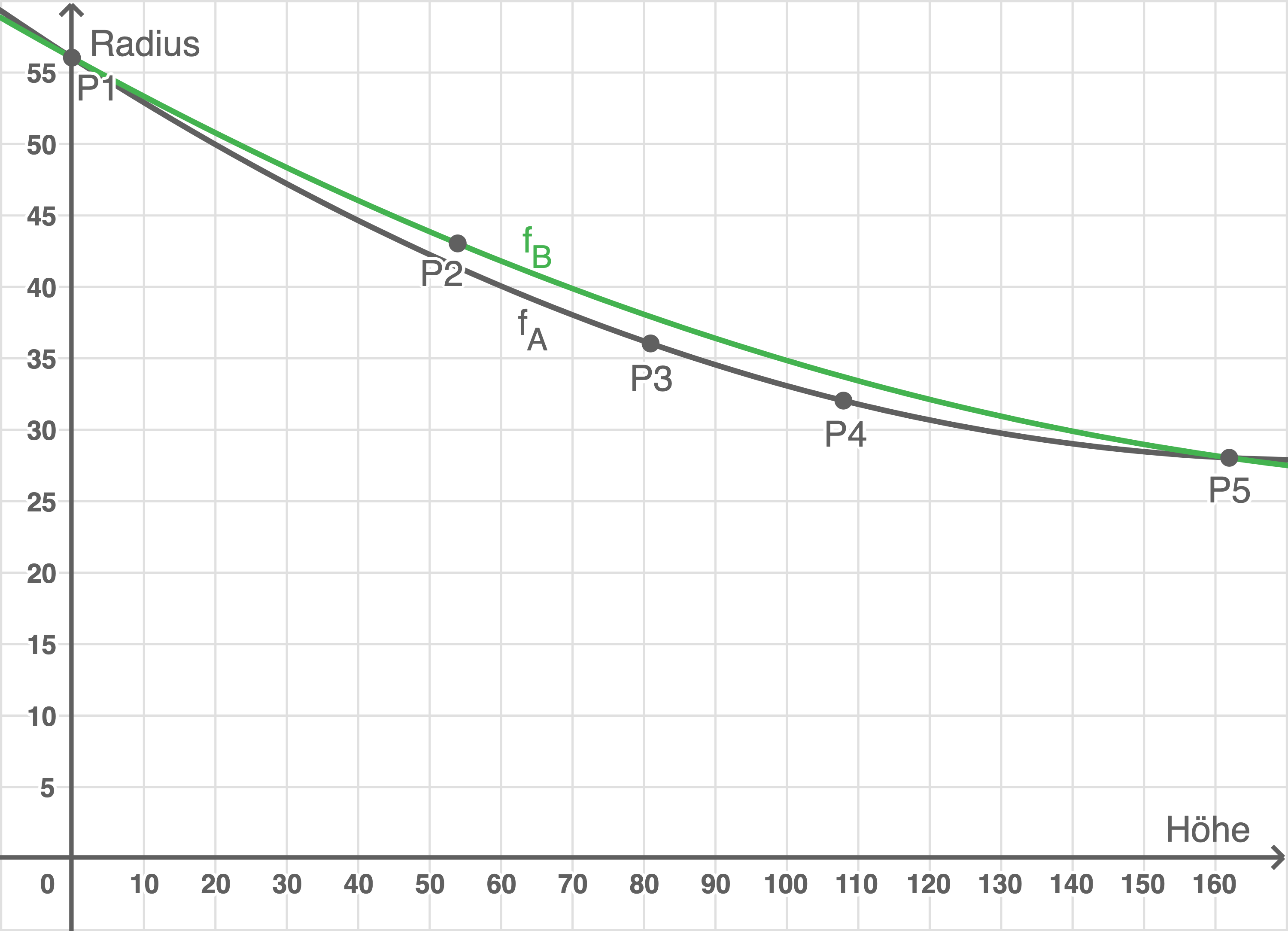 Qualität vergleichen
Es ist zu erkennen, dass der Graph von
Qualität vergleichen
Es ist zu erkennen, dass der Graph von  die qualitativ bessere Annäherung an die fünf Stützpunkte ist, da dieser vier der fünf Stützpunkte besitzt, wohingegen der Graph von
die qualitativ bessere Annäherung an die fünf Stützpunkte ist, da dieser vier der fünf Stützpunkte besitzt, wohingegen der Graph von  einen vergleichsweise hohen Abstand zu den Stützpunkten
einen vergleichsweise hohen Abstand zu den Stützpunkten  und
und  hat.
hat.



3.1
Die Funktionsgleichung von  kann mit Hilfe von kubischer Regression bestimmt werden.
kann mit Hilfe von kubischer Regression bestimmt werden.
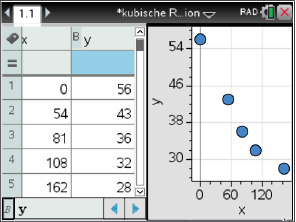
Die Koordinaten der Stützpunkte müssen hierfür im STAT-Menü unter  und
und  in den Taschenrechner eingespeichert werden.
Mit folgendem Befehl können nun die eingetragen Punkte angezeigt werden:
in den Taschenrechner eingespeichert werden.
Mit folgendem Befehl können nun die eingetragen Punkte angezeigt werden:
menu  3: Daten
3: Daten  6: Schnell Graph
6: Schnell Graph

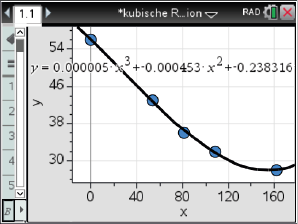
Mit dem Befehl zur kubischen Regression ergibt sich nun die gesuchte Funktionsgleichung:
 :
:
Menu  4: Analysieren
4: Analysieren  6: Regression
6: Regression  5: kubische Regression
5: kubische Regression
Somit ergibt sich für 
3.2
Der Umfang ist an der Stelle minimal, an der der Abstand des Graphen der Funktion  zur
zur  -Achse minimal ist.
Gesucht ist somit der Tiefpunkt der Funktion
-Achse minimal ist.
Gesucht ist somit der Tiefpunkt der Funktion  .
1.Schritt: Minimum bestimmen
Das Minimum der Funktion
.
1.Schritt: Minimum bestimmen
Das Minimum der Funktion  kann mit dem CAS bestimmt werden:
kann mit dem CAS bestimmt werden:
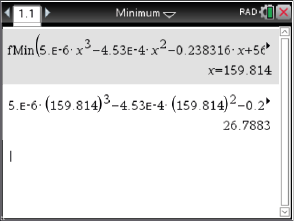 2.Schritt: Umfang berechnen
Der Wert der
2.Schritt: Umfang berechnen
Der Wert der  -Koordinate des Tiefpunkts entspricht dem Radius des gesuchten Umfangs.
Mit Hilfe der Umfangsformel folgt:
-Koordinate des Tiefpunkts entspricht dem Radius des gesuchten Umfangs.
Mit Hilfe der Umfangsformel folgt:
![\(\begin{array}[t]{rll}
U_{\text{min}} &=& 2 \cdot \pi \cdot r_{\text{min}} \\[5pt]
&=& 2 \cdot \pi \cdot 26,79 \\[5pt]
&=& 168,33 \, [\,\text{m}]
\end{array}\)](https://www.schullv.de/resources/formulas/88a4f2e49f9e1085f66cae44f8dc7759a7205d477be16ed00bd1a5c0d2ce09af_light.svg) Der minimale Umfang beträgt somit etwa
Der minimale Umfang beträgt somit etwa  Meter.
Meter.
Im Menu Funktionsminimum kann durch den Befehl fMin() die vollständige Funktion sowie die Variable  definiert werden und so das Minimum bestimmt werden.
Da der Befehl fMin() eine Annäherung ist, kann außerdem noch ein Startwert angegeben werden, falls ein unerwarteter Wert für ein Minimum ausgegeben wird.
definiert werden und so das Minimum bestimmt werden.
Da der Befehl fMin() eine Annäherung ist, kann außerdem noch ein Startwert angegeben werden, falls ein unerwarteter Wert für ein Minimum ausgegeben wird.
 Das Minimum folgt mit
Das Minimum folgt mit 

4.
Rechnung erläutern
Die Rechnung quadriert die Differenzen der Funktionswerte von  und der jeweiligen
und der jeweiligen  -Werte der Stützpunkte.
Da
-Werte der Stützpunkte.
Da  mit Hilfe der kubischen Regression erstellt wurde, liegen die hierfür verwendeten Stützwerte nicht genau auf dessen Graph.
Die Rechnung in der Aufgabenstellung gibt somit einen Wert für die Genauigkeit von
mit Hilfe der kubischen Regression erstellt wurde, liegen die hierfür verwendeten Stützwerte nicht genau auf dessen Graph.
Die Rechnung in der Aufgabenstellung gibt somit einen Wert für die Genauigkeit von  an.
Genauigkeit von
an.
Genauigkeit von  ermitteln
Mit dem CAS kann eine Wertetabelle der Funktion
ermitteln
Mit dem CAS kann eine Wertetabelle der Funktion  erstellt werden. Es folgt somit:
Ergebnisse deuten
Der Wert der Rechnung mit
erstellt werden. Es folgt somit:
Ergebnisse deuten
Der Wert der Rechnung mit  statt
statt  liefert mit
liefert mit  ein weitaus höheres Ergebnis als der in der Aufgabenstellung gegebene Wert von
ein weitaus höheres Ergebnis als der in der Aufgabenstellung gegebene Wert von  .
Der Graph von
.
Der Graph von  hat somit durchschnittlich einen größeren Abstand zu den Stützpunkten und ist folglich eine ungenauere Annäherung.
hat somit durchschnittlich einen größeren Abstand zu den Stützpunkten und ist folglich eine ungenauere Annäherung.
5.
Volumen bestimmen
Da die Wandstärke konstant  beträgt, hat die innere Randfunktion
beträgt, hat die innere Randfunktion  den gleichen Verlauf wie
den gleichen Verlauf wie  und ist lediglich um den Faktor
und ist lediglich um den Faktor  entlang der
entlang der  -Achse verschoben:
Das Volumen der Wand des Kühlturms entspricht dem Volumen des Rotationskörpers zwischen den Graphen von
-Achse verschoben:
Das Volumen der Wand des Kühlturms entspricht dem Volumen des Rotationskörpers zwischen den Graphen von  und
und  Dies kann mit folgender Formel berechnet werden:
Dies kann mit folgender Formel berechnet werden:
 Eingeben der Formel und der entsprechenden Funktionsterme von
Eingeben der Formel und der entsprechenden Funktionsterme von  und
und  in den CAS ergibt:
in den CAS ergibt:
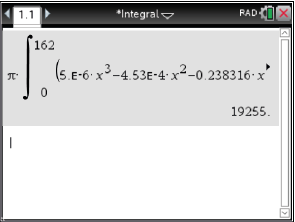 Der Bauschutt hat somit ein Volumen von
Der Bauschutt hat somit ein Volumen von  Masse berechnen
Aus der Aufgabenstellung kann entnommen werden, dass
Masse berechnen
Aus der Aufgabenstellung kann entnommen werden, dass  Bauschutt eine Masse von
Bauschutt eine Masse von  hat.
hat.
![\(\begin{array}[t]{rll}
m&=& 19255,23\text{ m}^3 \cdot 2400\frac{\text{kg}}{\text{m}^3}& \\[5pt]
&=& 46\, 212\,5 51\text{ kg}& \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/8f4a0442028e10b340cf0b9599248fdfb4e3c58b689d7524315e5da77dacdd41_light.svg) Der Bauschutt des Kühlturms wiegt somit
Der Bauschutt des Kühlturms wiegt somit  .
.

1.

2.
Funktion  bestimmen
Da drei Stützpunkte gegeben sind, handelt es sich hierbei um eine quadratische Funktionsgleichung. Eine Funktion höheren Grades würde mehr als drei Stützpunkte benötigen.
Allgemeine quadratische Funktion:
bestimmen
Da drei Stützpunkte gegeben sind, handelt es sich hierbei um eine quadratische Funktionsgleichung. Eine Funktion höheren Grades würde mehr als drei Stützpunkte benötigen.
Allgemeine quadratische Funktion:  Anhand der in der Aufgabenstellung gegebenen Stützpunkte kann nun ein lineares Gleichungssystem aufgestellt werden:
Anhand der in der Aufgabenstellung gegebenen Stützpunkte kann nun ein lineares Gleichungssystem aufgestellt werden:
![\(\begin{array}[t]{rll}
f_A(0)&=& 56 \\[5pt]
f_A(81)&=& 36 \\[5pt]
f_A(162)&=& 28 \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/2851b5fd4b16fb733b7374596de4f633c36836d8ec0f86617dc9a5ff7b7e78ff_light.svg) Gleichungssystem aufstellen:
Gleichungssystem aufstellen:
 Mit dem solve-Befehl des CAS ergibt sich:
Mit dem solve-Befehl des CAS ergibt sich:
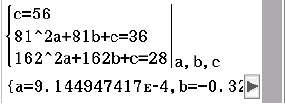 Für die Parameter ergibt sich folglich:
Für die Parameter ergibt sich folglich:


 Die Funktionsgleichung von
Die Funktionsgleichung von  folgt also mit:
folgt also mit:
 Funktion
Funktion  bestimmen
Analog zur Funktion
bestimmen
Analog zur Funktion  folgt:
folgt:
![\(\begin{array}[t]{rll}
f_B(0)&=& 56 \\[5pt]
f_B(54)&=& 43 \\[5pt]
f_B(162)&=& 28 \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/5eb3aed9ab4d718fc2f348f03e496bc331be4676ac7bfcfe474b6c21dc7c80b8_light.svg) Gleichungssystem aufstellen:
Gleichungssystem aufstellen:
 Mit dem CAS ergibt sich:
Mit dem CAS ergibt sich:
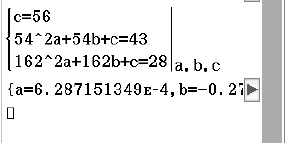 Für die Parameter ergibt sich folglich:
Für die Parameter ergibt sich folglich:


 Die Funktionsgleichung von
Die Funktionsgleichung von  folgt also mit:
folgt also mit:
 Graphen skizzieren
Die Funktionen können mit dem CAS angezeigt werden. Durch Erstellen von Wertetabellen mit dem CAS lassen sich außerdem Punkte bestimmen, anhand derer der Graph skizziert werden kann.
Graphen skizzieren
Die Funktionen können mit dem CAS angezeigt werden. Durch Erstellen von Wertetabellen mit dem CAS lassen sich außerdem Punkte bestimmen, anhand derer der Graph skizziert werden kann.
 Qualität vergleichen
Es ist zu erkennen, dass der Graph von
Qualität vergleichen
Es ist zu erkennen, dass der Graph von  die qualitativ bessere Annäherung an die fünf Stützpunkte ist, da dieser vier der fünf Stützpunkte besitzt, wohingegen der Graph von
die qualitativ bessere Annäherung an die fünf Stützpunkte ist, da dieser vier der fünf Stützpunkte besitzt, wohingegen der Graph von  einen vergleichsweise hohen Abstand zu den Stützpunkten
einen vergleichsweise hohen Abstand zu den Stützpunkten  und
und  hat.
hat.
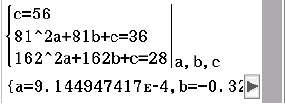
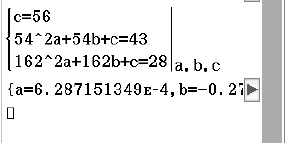

3.1
Die Funktionsgleichung von  kann mit Hilfe von kubischer Regression bestimmt werden.
kann mit Hilfe von kubischer Regression bestimmt werden.
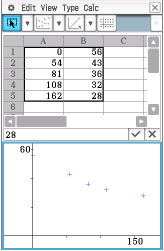
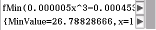
Die Koordinaten der Stützpunkte müssen hierfür im Spreadsheet unter  und
und  in den Taschenrechner eingespeichert werden.
Durch Markieren aller Koordinaten und anschließendem Klicken auf das Punkte-Symbol oberhalb des Bildschirms können nun die eingetragenen Punkte angezeigt werden.
in den Taschenrechner eingespeichert werden.
Durch Markieren aller Koordinaten und anschließendem Klicken auf das Punkte-Symbol oberhalb des Bildschirms können nun die eingetragenen Punkte angezeigt werden.

Aus dem oberen Bildschirmmenu kann die Regression mit  ausgewählt werden, sodass die Parameter
ausgewählt werden, sodass die Parameter  und
und  angezeigt werden.
Einfügen in die allgemeine Funktion dritten Grades ergibt:
angezeigt werden.
Einfügen in die allgemeine Funktion dritten Grades ergibt:
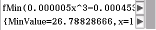
3.2
Der Umfang ist an der Stelle minimal, an der der Abstand des Graphen der Funktion  zur
zur  -Achse minimal ist.
Gesucht ist somit der Tiefpunkt der Funktion
-Achse minimal ist.
Gesucht ist somit der Tiefpunkt der Funktion  .
1.Schritt: Minimum bestimmen
Das Minimum der Funktion
.
1.Schritt: Minimum bestimmen
Das Minimum der Funktion  kann mit dem CAS bestimmt werden:
Im Menu Funktionsminimum kann durch den Befehl fMin die vollständige Funktion sowie die Variable
kann mit dem CAS bestimmt werden:
Im Menu Funktionsminimum kann durch den Befehl fMin die vollständige Funktion sowie die Variable  definiert werden und so das Minimum bestimmt werden.
Da der Befehl fMin() eine Annäherung ist, kann außerdem noch ein Startwert angegeben werden, falls ein unerwarteter Wert für ein Minimum ausgegeben wird.
definiert werden und so das Minimum bestimmt werden.
Da der Befehl fMin() eine Annäherung ist, kann außerdem noch ein Startwert angegeben werden, falls ein unerwarteter Wert für ein Minimum ausgegeben wird.

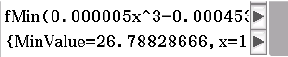 Das Minimum folgt mit
Das Minimum folgt mit  2.Schritt: Umfang berechnen
Der Wert der
2.Schritt: Umfang berechnen
Der Wert der  -Koordinate des Tiefpunkts entspricht dem Radius des gesuchten Umfangs.
Mit Hilfe der Umfangsformel folgt:
-Koordinate des Tiefpunkts entspricht dem Radius des gesuchten Umfangs.
Mit Hilfe der Umfangsformel folgt:
![\(\begin{array}[t]{rll}
U_{\text{min}} &=& 2 \cdot \pi \cdot r_{\text{min}} \\[5pt]
&=& 2 \cdot \pi \cdot 26,79 \\[5pt]
&=& 168,33 \, [\,\text{m}]
\end{array}\)](https://www.schullv.de/resources/formulas/88a4f2e49f9e1085f66cae44f8dc7759a7205d477be16ed00bd1a5c0d2ce09af_light.svg) Der minimale Umfang beträgt somit etwa
Der minimale Umfang beträgt somit etwa  Meter.
Meter.
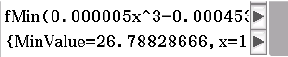
4.
Rechnung erläutern
Die Rechnung quadriert die Differenzen der Funktionswerte von  und der jeweiligen
und der jeweiligen  -Werte der Stützpunkte.
Da
-Werte der Stützpunkte.
Da  mit Hilfe der kubischen Regression erstellt wurde, liegen die hierfür verwendeten Stützwerte nicht genau auf dessen Graph.
Die Rechnung in der Aufgabenstellung gibt somit einen Wert für die Genauigkeit von
mit Hilfe der kubischen Regression erstellt wurde, liegen die hierfür verwendeten Stützwerte nicht genau auf dessen Graph.
Die Rechnung in der Aufgabenstellung gibt somit einen Wert für die Genauigkeit von  an.
Genauigkeit von
an.
Genauigkeit von  ermitteln
Mit dem CAS kann eine Wertetabelle der Funktion
ermitteln
Mit dem CAS kann eine Wertetabelle der Funktion  erstellt werden. Es folgt somit:
Ergebnisse deuten
Der Wert der Rechnung mit
erstellt werden. Es folgt somit:
Ergebnisse deuten
Der Wert der Rechnung mit  statt
statt  liefert mit
liefert mit  ein weitaus höheres Ergebnis als der in der Aufgabenstellung gegebene Wert von
ein weitaus höheres Ergebnis als der in der Aufgabenstellung gegebene Wert von  .
Der Graph von
.
Der Graph von  hat somit durchschnittlich einen größeren Abstand zu den Stützpunkten und ist folglich eine ungenauere Annäherung.
hat somit durchschnittlich einen größeren Abstand zu den Stützpunkten und ist folglich eine ungenauere Annäherung.
5.
Volumen bestimmen
Da die Wandstärke konstant  beträgt, hat die innere Randfunktion
beträgt, hat die innere Randfunktion  den gleichen Verlauf wie
den gleichen Verlauf wie  und ist lediglich um den Faktor
und ist lediglich um den Faktor  entlang der
entlang der  -Achse verschoben:
Das Volumen der Wand des Kühlturms entspricht dem Volumen des Rotationskörpers zwischen den Graphen von
-Achse verschoben:
Das Volumen der Wand des Kühlturms entspricht dem Volumen des Rotationskörpers zwischen den Graphen von  und
und  Dies kann mit folgender Formel berechnet werden:
Dies kann mit folgender Formel berechnet werden:
 Eingeben der Formel und der entsprechenden Funktionsterme von
Eingeben der Formel und der entsprechenden Funktionsterme von  und
und  in den CAS ergibt:
in den CAS ergibt:
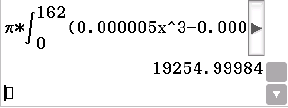 Der Bauschutt hat somit ein Volumen von
Der Bauschutt hat somit ein Volumen von  Masse berechnen
Aus der Aufgabenstellung kann entnommen werden, dass
Masse berechnen
Aus der Aufgabenstellung kann entnommen werden, dass  Bauschutt eine Masse von
Bauschutt eine Masse von  hat.
hat.
![\(\begin{array}[t]{rll}
m&=& 19255,23\text{ m}^3 \cdot 2400\frac{\text{kg}}{\text{m}^3}& \\[5pt]
&=& 46\, 212\,5 51\text{ kg}& \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/8f4a0442028e10b340cf0b9599248fdfb4e3c58b689d7524315e5da77dacdd41_light.svg) Der Bauschutt des Kühlturms wiegt somit
Der Bauschutt des Kühlturms wiegt somit  .
.