B2 – Analysis

Um Regenwasser zu speichern, wird es kontrolliert in ein unterirdisches Auffangbecken geleitet, das ein Fassungsvermögen von $800 \;\text{m}^3$ hat.
Für ein bestimmtes Regenereignis wird das Volumen des Regenwassers im Auffangbecken für $0 \leq x \leq 5$ modellhaft durch die in $\mathbb R$ definierte Funktion $v$ mit $v(x)=-\frac{5}{2} x^4+\frac{50}{3} x^3+190$ beschrieben. Dabei ist $x$ die seit Beobachtungsbeginn vergangene Zeit in Stunden und $v(x)$ das Wasservolumen in Kubikmetern.

1.1

Zeige, dass zu Beobachtungsbeginn das Wasservolumen im Auffangbecken $190 \;\text{m}^3$ beträgt, und bestimme das Volumen des Wassers, das in den ersten $1,5 \;\text{h}$ nach Beobachtungsbeginn in das Auffangbecken fließt.

(3 BE)

Betrachtet wird außerdem die in $\mathbb{R}$ definierte Funktion $r$ mit $r(x)=10x^2\cdot (5-x).$

1.2

Zeige, dass die momentane Änderungsrate des Volumens des Wassers im Auffangbecken in $\frac{\text{m}^3}{\text{h}}$ für den betrachteten Zeitraum durch $r$ beschrieben werden kann.

(3 BE)

1.3

Weise anhand des gegebenen Terms von $r$ nach, dass für den durch $0\lt x \lt5$ beschriebenen Zeitraum das Volumen des Wassers im Auffangbecken zu jedem Zeitpunkt zunimmt.

(3 BE)

1.4

Es wird geplant, zwei Stunden nach Beobachtungsbeginn eine Pumpe einzuschalten, die Wasser aus dem Auffangbecken mit einer konstanten Rate von $100\;\frac{\text{m}^3}{\text{h}}$ abpumpt. Die momentane Zuflussrate des Regenwassers in das Auffangbecken wird dabei weiterhin durch $r$ beschrieben. Eine Lösung $t$ der folgenden Gleichung hat im Sachzusammenhang eine Bedeutung.

$190+\displaystyle\int_0^2 r(x) \;\mathrm d x+\displaystyle\int_2^t(r(x)-100)\;\mathrm dx=400$

Gib diese Bedeutung von $t$ an und erläutere den Aufbau der Gleichung in Bezug auf diese Bedeutung.

(5 BE)

Gegeben sind die in $\mathbb{R}$ definierte Funktion $f$ mit $f(x)=x^2 \cdot(x-5)^2$ und die Stelle $x_W=\frac{15-5\sqrt{3}}{6}.$

2.1

Weise rechnerisch nach, dass $x_W$ eine Wendestelle von $f$ ist.

(3 BE)

2.2

Es gibt im ersten Quadranten ein Flächenstück, das von der $y$ -Achse, dem Graphen von $f$ und der Gerade parallel zur $x$ -Achse, die durch den Wendepunkt $(x_W \mid f (x_W ))$ verläuft, eingeschlossen wird.
Bestimme den Inhalt dieses Flächenstücks.

(3 BE)

2.3

Abbildung 1 zeigt den Graphen von $f.$

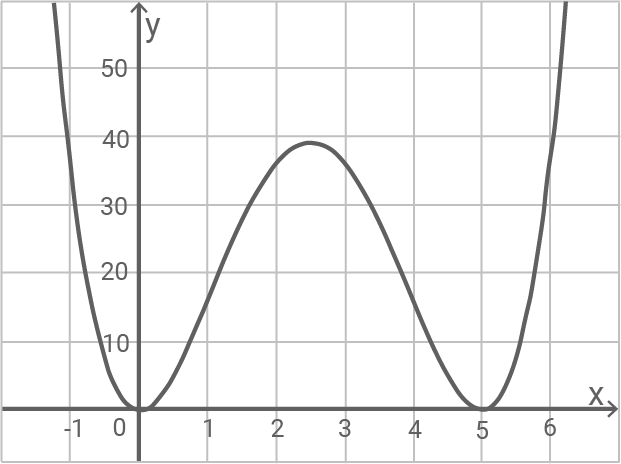
Abbildung 1

Die Punkte $A(u \mid f(u)), B(1 \mid 0), C(4 \mid 0)$ und $D(5-u \mid f(5-u))$ sind für jeden Wert von $u$ mit $0\lt u \lt 2,5$ die Eckpunkte eines symmetrischen Trapezes.
Skizziere das symmetrische Trapez für $u=1,5$ in die Abbildung. Ermittle einen Term, der den Flächeninhalt des symmetrischen Trapezes in Abhängigkeit von $u$ angibt.

(5 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1

Volumen zum Zeitpunkt $\boldsymbol{x=0}$ berechnen

$v(0)=190 \left[\text{m}^3 \right]$

Volumen des Wassers in den ersten $\boldsymbol{1,5}$ Stunden berechnen

$\begin{array}[t]{rlll} v(1,5)-190 &=& \dfrac{1395}{32} \\[5pt] &\approx& 44 \left[\text{m}^3 \right] \end{array}$

Es fließen etwa $44 \; \text{m}^3$ Wasser in das Auffangbecken.

1.2

$\(\begin{array}[t]{rlll} v$

1.3

Im Intervall $0\lt x\lt 5$ sind sowohl $10 x^2$ als auch $5-x$ stets positiv. Daher ist auch $r(x)$ immer positiv. Das bedeutet, dass $v$ in diesem Bereich streng monoton steigt - das Wasservolumen also zu keinem Zeitpunkt abnimmt.

1.4

Zu Beginn der Pumpentätigkeit befindet sich ein Wasservolumen von $400 \;\text{m}^3$ im Becken. Dieses Anfangsvolumen wird durch die ersten beiden Summanden erfasst. Die Funktion $r(x)-100$ beschreibt, wie schnell sich das Wasservolumen unter dem Einfluss der laufenden Pumpe verändert - angegeben in Kubikmetern pro Stunde.

Der Term $\displaystyle\int_2^t(r(x)-100) \; \mathrm{d} x$ gibt den Zuwachs oder Verlust an Wasser im Zeitraum ab dem Einschalten der Pumpe (ab $x=2$ ) bis zum gewählten Zeitpunkt $t$ an.

2.1

Berechnung der ersten, zweiten und dritten Ableitung von $\boldsymbol{f(x)}$ mithilfe des CAS

$\(\begin{array}[t]{rlll} f$

Berechnung der notwendigen Bedingung

$\(f$

Berechnung der hinreichenden Bedingung

$\(f$

Da beide Bedingungen erfüllt sind, ist die Stelle $x_W$ eine Wendestelle von $f.$

2.2

Die Fläche wird von der Geraden, die durch den Wendepunkt $x_W$ verläuft, und vom Graphen der Funktion $f$ eingeschlossen. Somit muss die Fläche unter $f$ von der Fläche unter der Geraden im Intervall $\left[ 0; \frac{15-5\sqrt{3}}{6}\right]$ abgezogen werden.

Durch Ausrechnen mit dem CAS folgt:

$\begin{array}[t]{rlll} \displaystyle\int_0^{\frac{15-5 \sqrt{3}}{6}}\left(f\left(\frac{15-5 \sqrt{3}}{6}\right)-f(x)\right) \;\mathrm{d} x &\approx& 11,4 \end{array}$

2.3

Das symmetrische Trapez einzeichnen

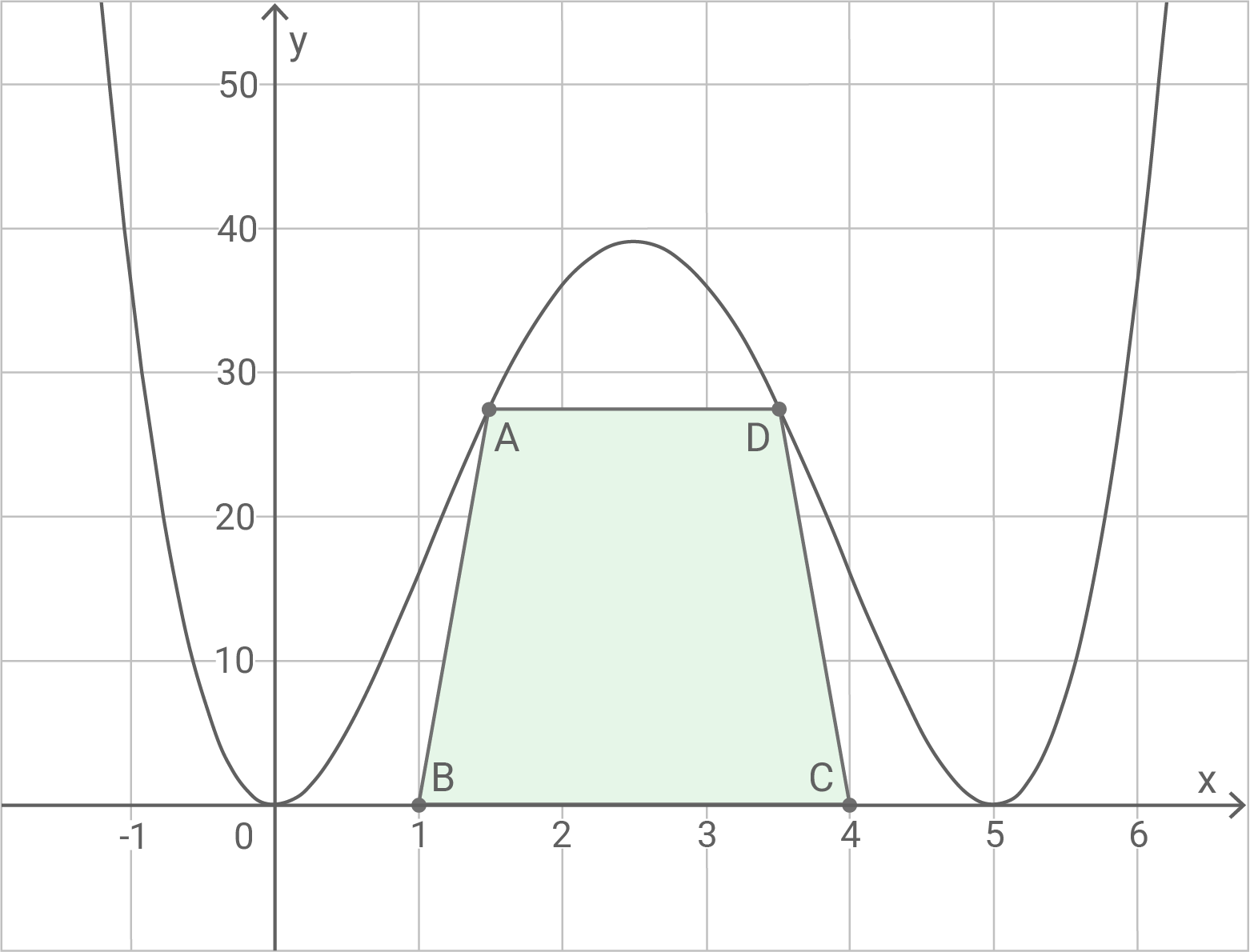
Abbildung

Term, der den Flächeninhalt angibt, bestimmen

Da die $y$ -Koordinaten identisch sind, reicht es aus, den Abstand zwischen den $x$ -Koordinaten zu berechnen.

Länge der Strecke $\overline{BC}$ berechnen

$\begin{array}[t]{rlll} \overline{BC} &=& C-B \\[5pt] &=& 4-1 \\[5pt] &=& 3 \end{array}$

Länge der Strecke $\overline{AD}$ berechnen

$\begin{array}[t]{rlll} \overline{AD} &=& D-A \\[5pt] &=& 5-u-u\\[5pt] &=& 5-2u \end{array}$

Die Höhe des Trapezes ergibt sich aus dem Funktionswert an der Stelle $u$ , also $f(u)$ . Die beiden parallelen Seiten des Trapezes haben die Längen 3 (für $\overline{B C}$ ) und $5-2 u$ (für $\overline{A D}$ ). Daraus folgt für den Flächeninhalt des Trapezes die Formel:

$\dfrac{1}{2} \cdot(3+5-2 u) \cdot f(u)$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?