B1 – Analysis

Eine Skisprungschanze besteht aus den Abschnitten Anlauf (inkl. Schanzentisch), Aufsprungbahn und Auslauf (Abbildung 1). Für den Neubau einer Skisprungschanze dient das Profil des Sprungturms in Abbildung 2 als Vorbild.

Die Profillinien des Anlaufs und der Aufsprungbahn sollen jeweils mit Hilfe des Graphen einer ganzrationalen Funktion modelliert werden. In der Modellierung liegt der höchste Punkt der Profillinie des Anlaufs auf der $y$ -Achse. Im Folgenden entspricht eine Längeneinheit einem Meter.

In der Modellierung beginnt die Profillinie des Anlaufs bei $x=0$ auf einer Höhe von $150 \,\text{m}.$ Der Endpunkt der Profillinie des Schanzentischs befindet sich im Punkt $(100 \mid 100),$ an dem die Steigung $-0,176$ beträgt (Abbildung 2).

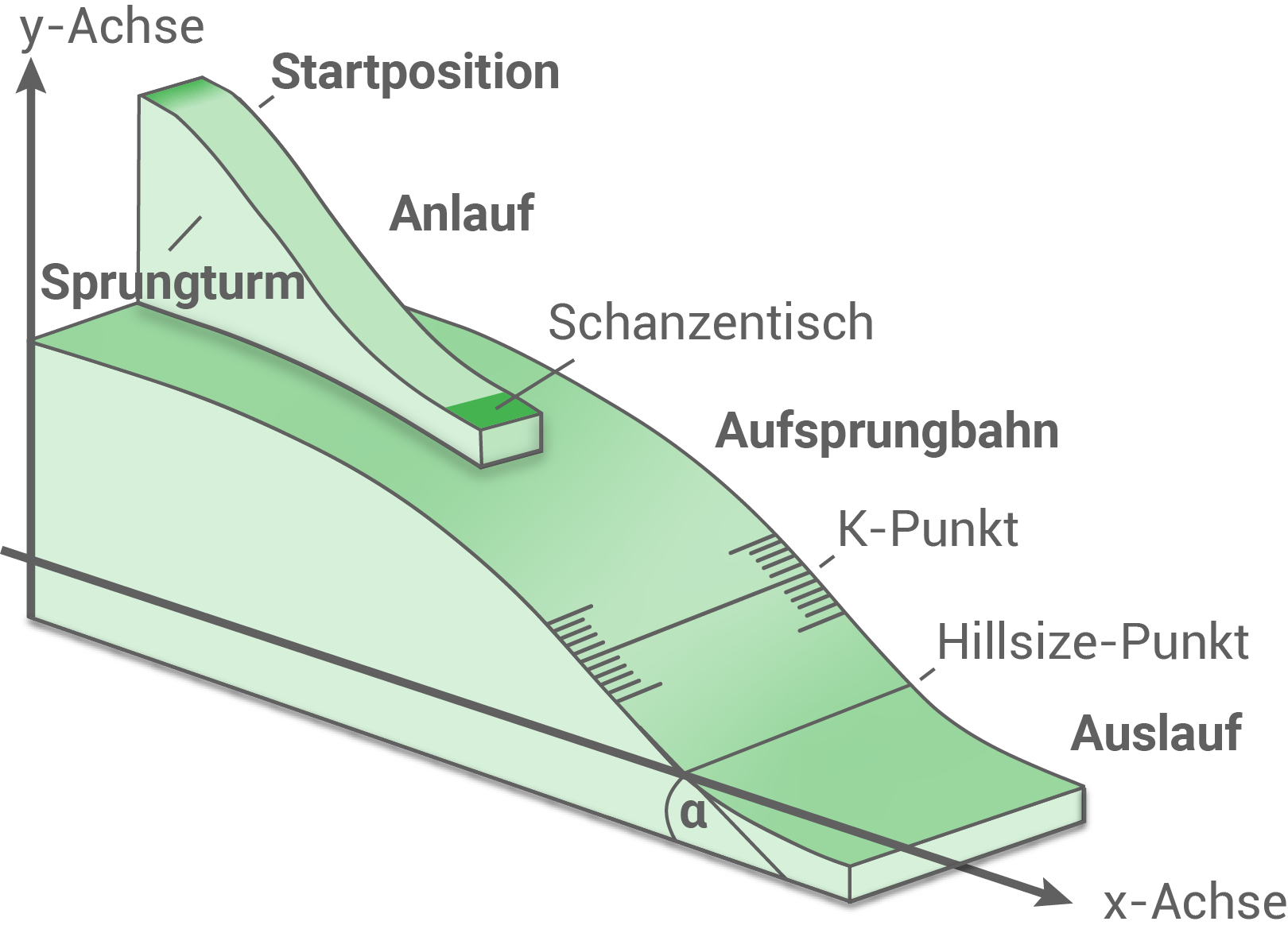
Schematische Darstellung eines Skisprungschanzens mit verschiedenen Elementen und Achsen.

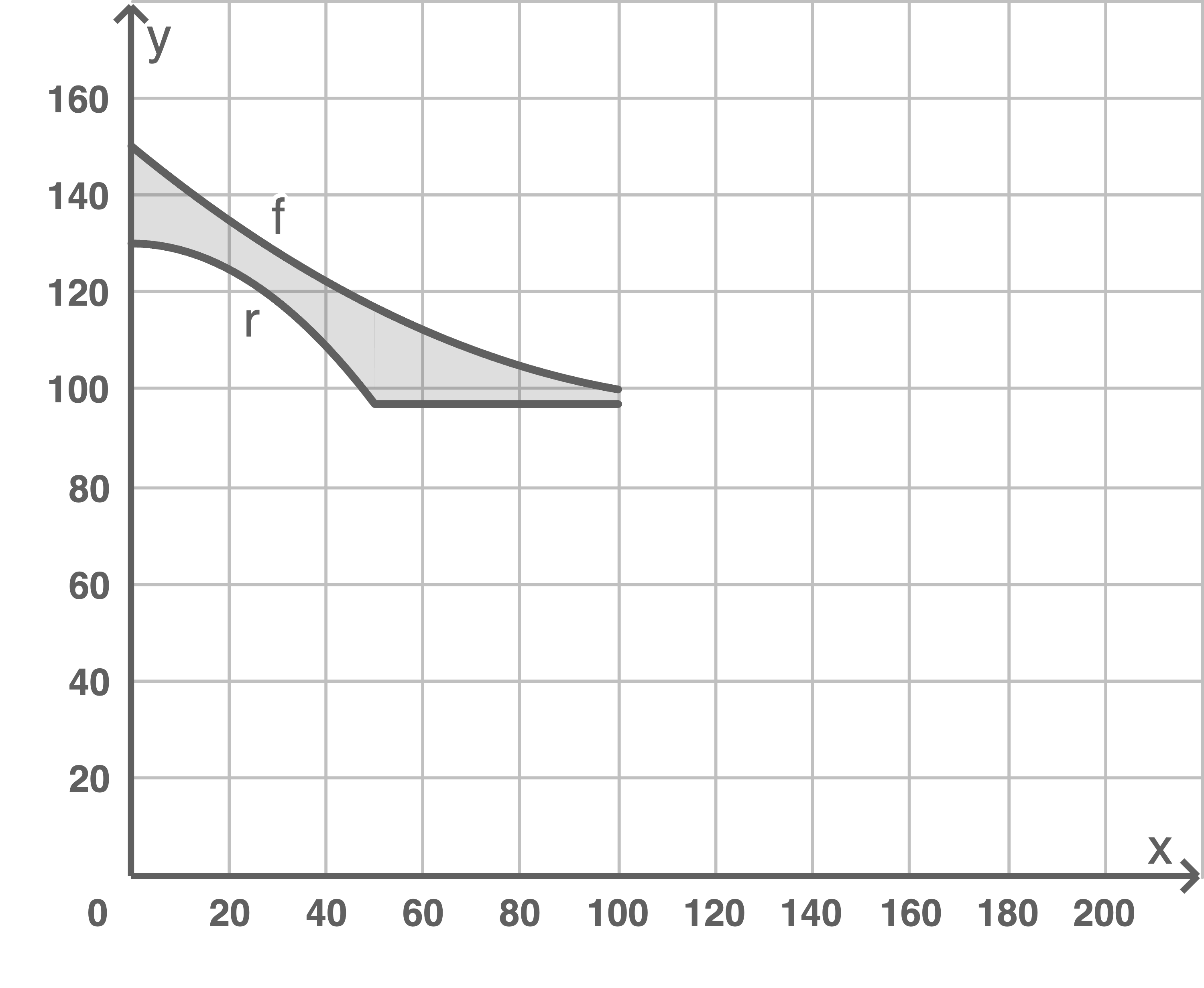
Abbildung 1: Abschnitte und charakteristische Punkte einer Skisprungschanze, schematisch

Grafik mit zwei Kurven und einem schattierten Bereich im Koordinatensystem. Beschriftungen an den Achsen.

Abbildung 2: Profil des Sprungturms

1.1

Die Profillinie des Anlaufs soll mit Hilfe des Graphen einer ganzrationalen Funktion $f$ zweiten Grades modelliert werden.

Leite aus den Angaben zur Modellierung das lineare Gleichungssystem, mit dem die Funktionsgleichung der Funktion $f$ ermittelt werden kann, her.

(4 BE)

Im Folgenden soll die Profillinie des Anlaufs durch den Graphen der Funktion $f$ mit $f(x)=0,00324 \cdot x^2-0,824 \cdot x+150$ modelliert werden.

1.2

Die Startposition der Skispringer befindet sich unterhalb des höchsten Punkts der Profillinie des Anlaufs bei $x=20$ .

Berechne die Steigung des Anlaufs an dieser Position.

(3 BE)

Im Modell befindet sich die Profillinie der Aufsprungbahn im Bereich $100 \leq x \leq 200.$

Ihr Verlauf wird durch den Graphen der Funktion $g$ mit

Funktionsgleichung anzeigen

$g(x)=\,...$

modelliert.

2.1

Im sogenannten Konstruktions-Punkt (K-Punkt, Abbildung 1) ist die Profillinie der Aufsprungbahn am steilsten.

Bestimme im Modell die Koordinaten des K-Punkts und den Abstand des K-Punkts vom Endpunkt der Profillinie des Schanzentischs.

Hinweis: Eine Randwertbetrachtung ist nicht erforderlich.

(4 BE)

2.2

Der sogenannte Hillsize-Punkt liegt bei $y=0$ auf der Profillinie der Aufsprungbahn und dient als Bezugspunkt für Höhenangaben. Im Hillsize-Punkt muss der Neigungswinkel $\alpha$ mindestens $32^{\circ}$ betragen (Abbildung 1).

Nach diesem Punkt wird die Landung durch einen zu flachen Neigungswinkel der Aufsprungbahn kritisch.

Bestimme die Lage des Hillsize-Punkts $H$ und prüfe, ob die vorliegende Modellierung die Bedingung an den Neigungswinkel im Punkt $H$ erfüllt.

(5 BE)

2.3

Bestimme den Höhenunterschied zwischen dem Ende des Schanzentischs und dem Anfang der Aufsprungbahn anhand der zugehörigen Profillinien und der Informationen aus Aufgabe 1 und 2.

Zeichne den Verlauf der Profillinie der Aufsprungbahn unter Verwendung der bisherigen Ergebnisse in die Abbildung 2 ein.

(5 BE)

2.4

Die möglichen Flugbahnen eines Skispringers können für $a \gt 0$ im Modell durch geeignete Ausschnitte der Graphen der Funktionenschar $p_a$ mit

Funktionsgleichung anzeigen

$p_a(x)=\,...$

dargestellt werden.

Erläutere im Sachzusammenhang, welchen Einfluss der Parameter $a$ auf die Flugbahn des Skispringers hat.

Ermittle den Wert von $a,$ für den der Skispringer im Hillsize-Punkt landet.

(5 BE)

2.5

Beschreibe den Verlauf der Graphen der Funktionenschar $p_a$ für $a \to \infty$ und begründe diesen Verlauf anhand des Funktionsterms.

(3 BE)

2.6

Ermittle, für welchen Wert von $a$ ein Skispringer im Modell im Punkt $(180 \mid g(180))$ der Profillinie der Aufsprungbahn landet.

(3 BE)

Der Sprungturm ist eine Betonkonstruktion, die im Bereich $0 \leq x \leq 50$ ohne Stütze in die Luft ragt (Abbildung 2).

Die untere Profillinie des Sprungturms kann in diesem Bereich durch den Graphen der Funktion $r$ mit $r(x)=130-\dfrac{33}{2500} \cdot x^2$ modelliert werden.

Für $50 \leq x \leq 100$ beschreibt die Gerade $y=97$ die untere Profillinie des Sprungturms (Abbildung 2).

Bestimme den Inhalt $A$ der durch das Profil beschriebenen Seitenfläche des Sprungturms.

(3 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1

Aus den gegebenen Informationen lässt sich folgendes Gleichungssystem aufstellen:

$\(\begin{array}{lrll} \text{I:}\quad&f(0)&=& 150 & \\ \text{II:}\quad&f(100)&=& 100 &\quad \\ \text{III:}\quad&f$

Eine ganzrationale Funktion zweiten Grades besitzt folgende Form:

$f(x) = ax^2 + bx + c$

Einsetzen der ersten Bedingung liefert:

$\begin{array}[t]{rll} f(0)&=& 150 & \\[5pt] a\cdot0^2 + b\cdot0 + c&=& 150 & \\[5pt] c&=& 150 \end{array}$

Mit der zweiten Bedingung sowie mit $c=150$ folgt:

$b= -0,5-100a$

Rechenweg anzeigen

Für die Ableitung von $f$ gilt:

$\(f$

Einsetzen der dritten Bedingung liefert:

$a=0,00324$

Rechenweg anzeigen

Der Parameter $b$ ergibt sich also zu:

$\begin{array}[t]{rll} b&=& -0,5-100a & \\[5pt] &=& -0,5-100\cdot 0,00324 & \\[5pt] &=& -0,824 \end{array}$

Alternativ können die Parameter direkt durch Lösen des Gleichungssystems mit dem CAS bestimmt werden.

Die Funktionsgleichung der Funktion $f$ ist somit gegeben durch:

$f(x)=0,00324\cdot x^2-0,824\cdot x+150$

1.2

Ableitung bestimmen:

$\(f$

An der Stelle $x=20$ gilt also:

$\(\begin{array}[t]{rll} m&=& f$

Die Steigung des Anlaufs an der Position $x=20$ beträgt somit etwa $m=-0,69.$

2.1

1. Schritt: Ableitungen bestimmen

$\(g$

2. Schritt: Hinreichende Bedingung für Wendestellen anwenden

$x \approx 157,8$

Rechenweg anzeigen

Aus der Aufgabenstellung geht hervor, dass genau ein $K$ -Punkt und somit genau eine Wendestelle existiert. Auf das Anwenden der hinreichenden Bedingung kann somit verzichtet werden.

3. Schritt: $\boldsymbol{y}$ -Koordinate berechnen

Mit dem CAS ergibt sich:

$g(157,8)\approx 46$

Die Koordinaten des K-Punkts sind somit gegeben durch $K(157,8\mid 46).$

4. Schritt: Abstand bestimmen

Der Endpunkt der Profillinie besitzt die Koordinaten $E(100 \mid 100).$

Für den Abstand $d$ der beiden Punkte gilt also:

$d(K;E) \approx 79,1 \; [\text{m}]$

Rechenweg anzeigen

Der Abstand des K-Punkts zum Endpunkt der Profillinie des Schanzentischs beträgt etwa 79,1 Meter.

2.2

Lage des Hillsize-Punkts bestimmen

Für den Hillsize-Punkt soll gelten:

$g(x_H)=0$

Mit dem CAS ergibt sich im betrachteten Bereich: $x_H=200.$

Bedingung überprüfen

Für den Neigungswinkel $\alpha$ im Hillsize-Punkt $H$ gilt $\tan(\alpha)=m,$ wobei $m$ die Steigung von $g$ im Punkt $H$ ist.

Es gilt:

$m \approx -0,62$

Rechenweg anzeigen

Somit folgt:

$\begin{array}[t]{rll} \tan(\alpha)&=& m & \\[5pt] \tan(\alpha)&\approx & -0,62 &\quad \scriptsize \mid\; \tan^{-1}\\[5pt] \alpha &=& 31,8 \, ^\circ \end{array}$

Die vorliegende Modellierung erfüllt die Bedingung, dass der Neigungswinkel im Hillsize-Punkt mindestens $32\,^\circ$ betragen muss, somit nicht.

2.3

Höhenunterschied bestimmen

Das Ende des Schanzentischs befindet sich laut Aufgabenstellung im Punkt $(100\mid 100)$ und somit gilt für die Höhe $h_E=100\, [\text{m}].$

Die Aufsprungbahn beginnt an der Stelle $x=100.$ Für die Höhe $h_A$ an dieser Stelle gilt:

$h_A= 97 \; [\text{m}]$

Rechenweg anzeigen

Der Höhenunterschied ist somit gegeben durch $100\;\text{m} -97 \;\text{m} =3 \;\text{m}.$

Verlauf zeichnen

Aus den vorherigen Aufgaben ist für $g(x)$ bekannt:

$100 \leq x \leq 200$
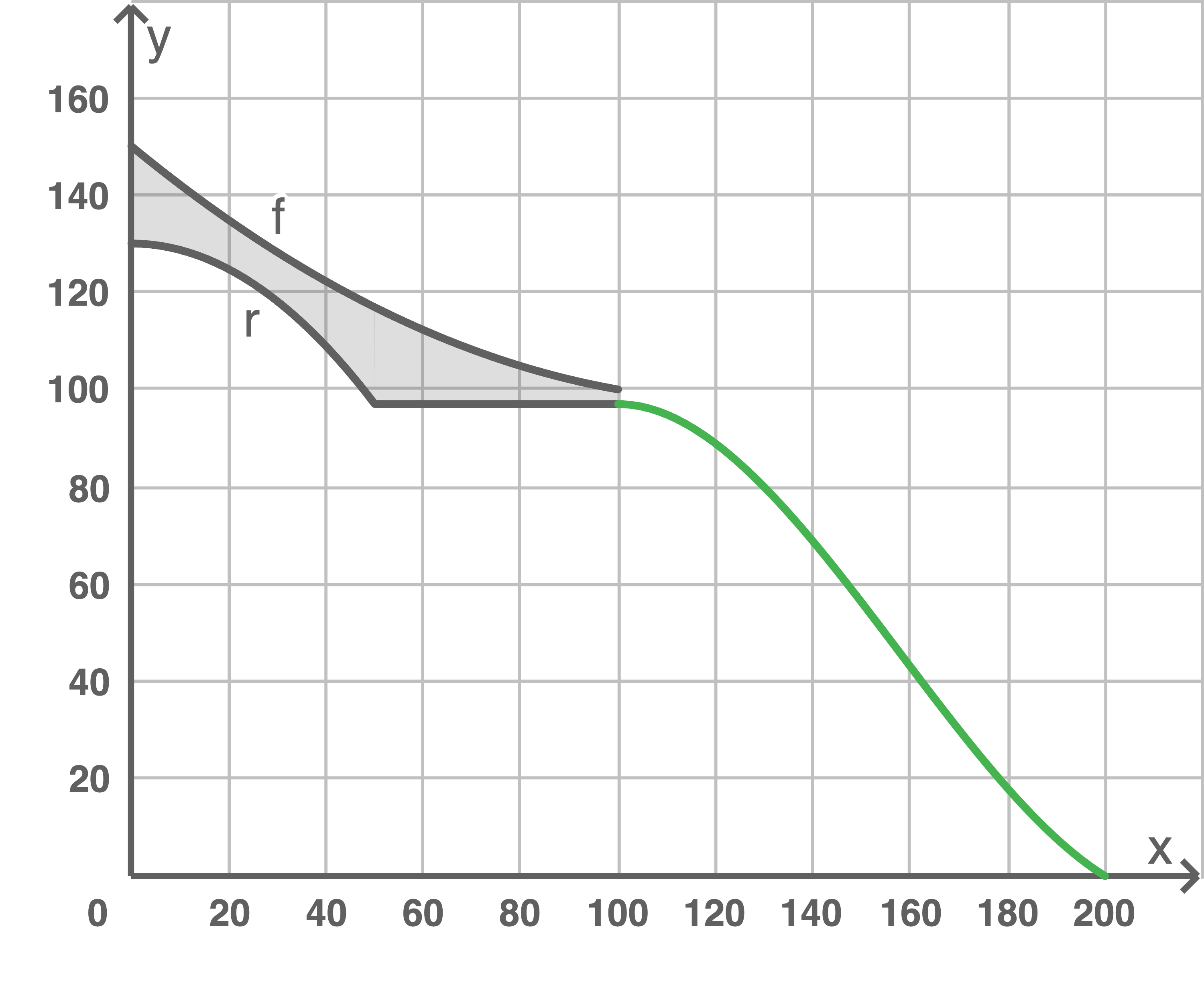
Wendepunkt $K(157,8\mid 46)$
$g(100)=97$
$g(200)=0$

Mit dem CAS kann der Graph von $g$ außerdem dargestellt werden.

Der Verlauf der Profillinie der Aufsprungbahn kann somit wie folgt eingezeichnet werden:

Diagramm mit zwei Funktionen und einer Fläche, die zwischen ihnen eingezeichnet ist. Achsen beschriftet mit x und y.

2.4

Einfluss des Parameters erleutern

Der Parameter $a$ beeinflusst den Ausdruck $\dfrac{5,083}{a^2} \cdot(x-100)^2,$ der die Form der Parabel festlegt. Wenn der Wert von $a$ größer wird, nimmt der Wert von $\dfrac{5,083}{a^2}$ ab, wodurch die Parabel breiter und flacher wird.

Bei größeren Werten von $a$ ist die Flugkurve somit gestreckter und der Skispringer hat eine flachere Flugbahn. Bei kleineren Werten von $a$ wird die Parabel steiler, was auf eine kürzere und steilere Flugbahn hindeutet.

Wert von $\boldsymbol{a}$ ermitteln

Damit der Skispringer im Hillsize-Punkt landet, muss gelten:

$p_a(200)= 0$

Vollständigen Rechenweg anzeigen

Mit dem CAS ergibt sich $a\approx 24,8.$

2.5

Der Funktionsterm setzt sich aus dem konstanten Term $117,63,$ dem quadratischen Term $-\dfrac{5,083}{a^2} \cdot (x - 100)^2$ und dem linearen Term $-0,1763 \cdot x$ zusammen.

Für $a\rightarrow \infty$ nähert sich der quadratische Term null an, während der konstante und lineare Term unverändert bleiben.

Der Term lässt sich somit für $a\rightarrow \infty$ annähernd vereinfachen zu:

$p_a(x) \approx 117,63 - 0,1763 \cdot x$

Der Graph dieser Funktion entspricht einer Geraden mit der negativen Steigung $m=-0,1763.$ Die Parabeln, die durch die quadratischen Terme erzeugt werden, verlieren ihre Breite und ihre Biegung, sodass die Funktion mit wachsendem $a$ nahezu linear wird.

2.6

Mit dem CAS ergibt sich:

$g(180)\approx 18,02$

Damit der Skispringer im Punkt $(180 \mid g(180))$ landet, muss also gelten:

$p_a(180)= 18,02$

Mit dem solve-Befehl des CAS ergibt sich:

$a \approx 21,9$

Die Seitenfläche des Sprungturms kann in zwei Abschnitte unterteilt werden.

Für $0\leq x \leq 50$ gilt: $A_1= \displaystyle\int_{0}^{50}(f(x)-r(x))\;\mathrm dx$

Für $50\leq x \leq 100$ gilt: $A_2= \displaystyle\int_{50}^{100}(f(x)-97)\;\mathrm dx$

Der Flächeninhalt ergibt sich mit dem CAS somit zu:

$\begin{array}[t]{rll} A&=&A_1+A_2 & \\[5pt] &= &655+505 & \\[5pt] &=& 1160 \, [\text{m}^2] \end{array}$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?