A - Hilfsmittelfreier Teil

Analysis - Niveau 1

In Abbildung 1 sind der Graph der Funktion $g$ mit $g(x)= \dfrac{1}{3}x^2 -\dfrac{2}{3}x+\dfrac{4}{3}$ sowie der Graph einer weiteren Funktion $f$ dargestellt.

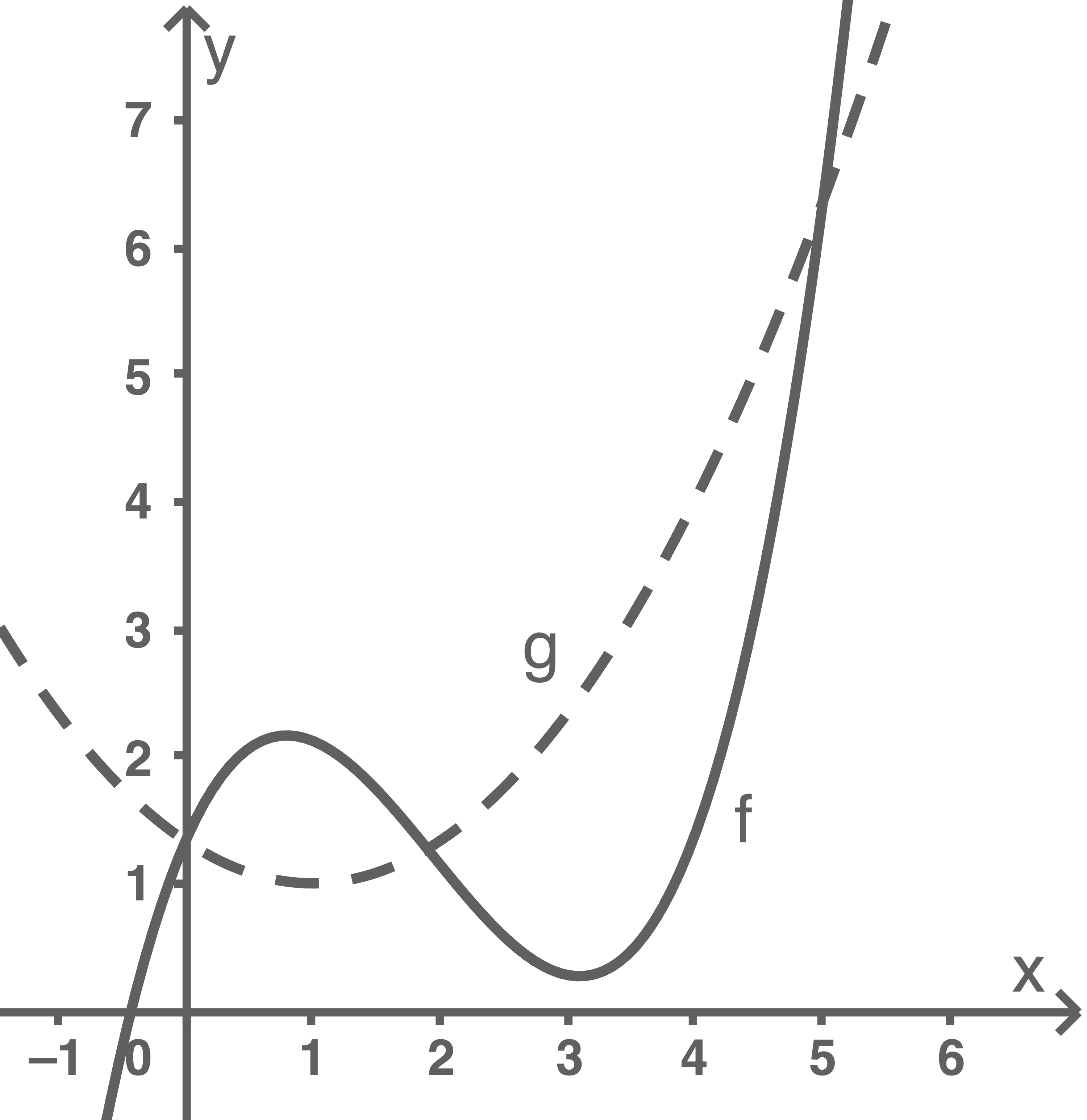
Abbildung 1

1.1

Berechne $\displaystyle\int_{0}^{3}g(x)\;\mathrm dx$ und zeichne die Fläche, deren Inhalt mit dem Integral berechnet wird, in Abbildung 1 ein.

(3 BE)

1.2

Entscheide nur anhand der Abbildung 1, ob der Wert des Integrals $\displaystyle\int_{2}^{5}\left(f(x)-g(x)\right)\;\mathrm dx$ eine positive Zahl, eine negative Zahl oder gleich null ist.

(2 BE)

Stochastik - Niveau 1

In einem Behälter befinden sich 2 blaue und 3 weiße Kugeln.

2.1

Zwei Kugeln werden nacheinander zufällig ohne Zurücklegen gezogen.

Gib für die folgenden Ereignisse jeweils einen Term zur Berechnung der Wahrscheinlichkeit an:

$A:$

„Beide Kugeln sind blau.“

$B:$

„Mindestens eine Kugel ist weiß.“

$C:$

„Eine Kugel ist weiß und eine blau.“

(3 BE)

2.2

Bestimme, wie viele grüne Kugeln zusätzlich in den Behälter gelegt werden müssen, damit die Wahrscheinlichkeit, beim einmaligen Ziehen zufällig eine grüne Kugel zu ziehen, $\dfrac{2}{3}$ beträgt.

(2 BE)

Lineare Algebra/Analytische Geometrie - Niveau 1

Gegeben sind die Punkte $A(5\mid 7\mid 2), B(3\mid 10\mid 3), C(4\mid 7\mid 7)$ und $D(6\mid 4\mid 6).$

3.1

Zeige, dass das Viereck $ABCD$ ein Parallelogramm, aber kein Rechteck ist.

(3 BE)

3.2

Bestimme die Koordinaten des Mittelpunkts $M$ der Diagonalen $\overline{AC}.$

(2 BE)

Lineare Algebra/Analytische Geometrie - Niveau 2

Gegeben sind die Punkte $A(-6\mid 8\mid 1)$ und $B(-3\mid 8\mid -5)$ sowie eine Gleichung der Geraden $g$ mit

$g:\, \overrightarrow{x} = \pmatrix{-1\\2\\1} + r\pmatrix{2\\-3\\1},$ $r\in \mathbb{R}.$

Bestätige, dass die Strecke $\overline{AB}$ von der Geraden $g$ geschnitten wird.

(5 BE)

Analysis- Niveau 1

1.1

Integral berechnen

$\displaystyle\int_{0}^{3}g(x)\;\mathrm dx= 4 \; [\text{FE}]$

Rechenweg anzeigen

Fläche einzeichnen

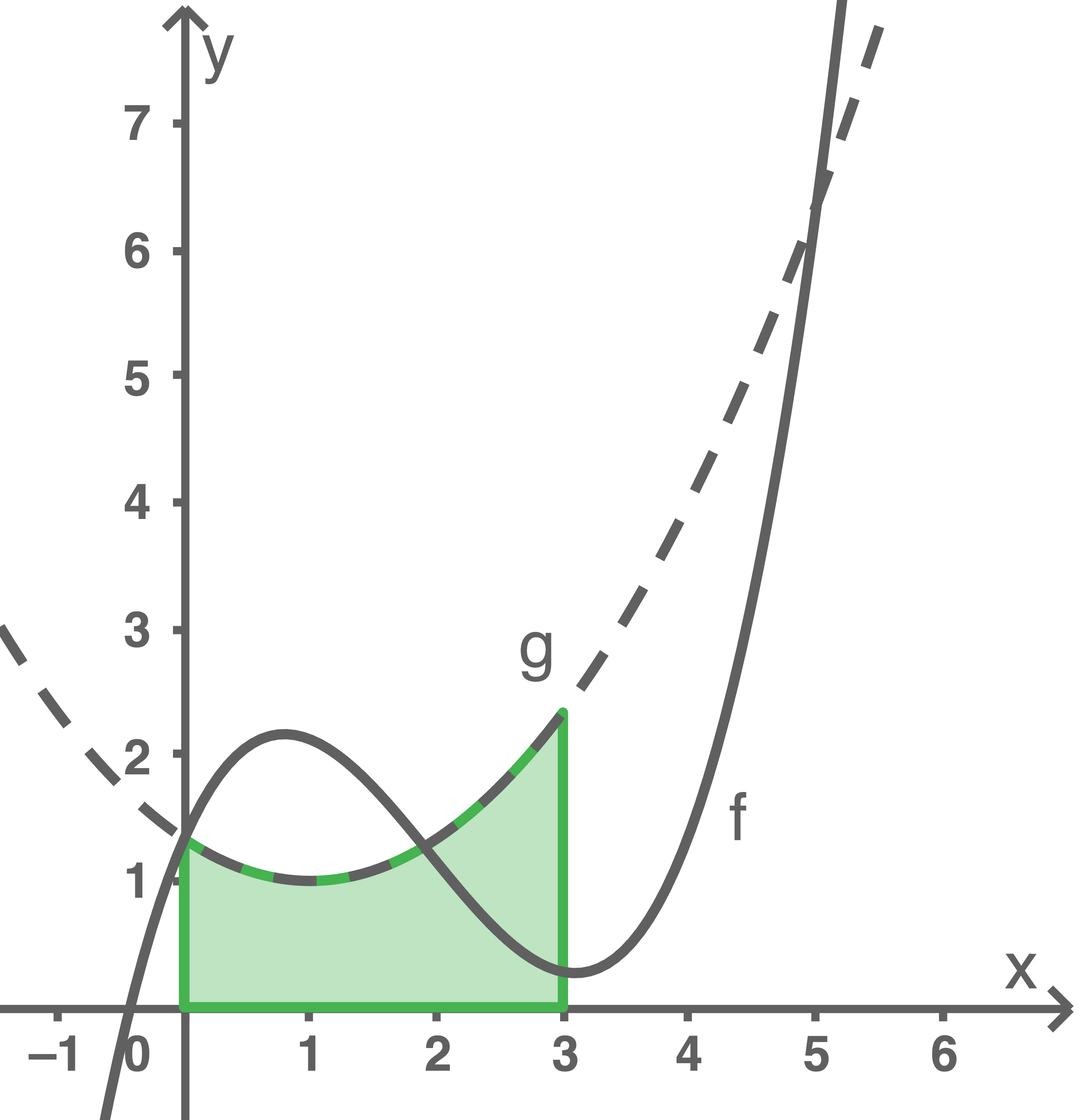
1.2

Der Graph von $f$ verläuft im Intervall $[2 ; 5]$ ausschließlich unterhalb des Graphen von $g.$ Somit ist der zugehörige Inhalt der Fläche unter dem Graphen von $f$ kleiner als der Inhalt der entsprechenden Fläche unter dem Graphen von $g.$

Der Wert des Integrals ist somit negativ.

Stochastik - Niveau 1

2.1

$b:$ „Es wird eine blaue Kugel gezogen.“

$w:$ „Es wird eine weiße Kugel gezogen.“

Mit den Pfadregeln folgt:

$\begin{array}[t]{rll} P(A)&=& P(b,b) &\\[5pt] &=& \dfrac{2}{5}\cdot \dfrac{1}{4} &\\[5pt] &=& \dfrac{1}{10} \end{array}$

$\begin{array}[t]{rll} P(B)&=& P(w,w)+ P(w,b)+P(b,w) &\\[5pt] &=&\dfrac{3}{5}\cdot \dfrac{2}{4} + \dfrac{3}{5}\cdot \dfrac{2}{4} +\dfrac{2}{5}\cdot \dfrac{3}{4} &\\[5pt] &=&\dfrac{9}{10} \end{array}$

Alternativ:

$\begin{array}[t]{rll} P(B)&=& 1-P(b,b) &\\[5pt] &=& \dfrac{9}{10} \end{array}$

$\begin{array}[t]{rll} P(C) &=& P(w,b)+P(b,w) &\\[5pt] &=& \dfrac{3}{5}\cdot \dfrac{2}{4} + \dfrac{2}{5}\cdot \dfrac{3}{4} &\\[5pt] &=& \dfrac{3}{5} \end{array}$

2.2

Werden $x$ grüne Kugeln hinzugefügt, dann befinden sich $5+x$ Kugeln im Behälter.

Die Wahrscheinlichkeit, eine grüne Kugel zu ziehen, beträgt dann $\dfrac{x}{5+x}.$

Gleichsetzen mit $\dfrac{2}{3}$ liefert:

$\begin{array}[t]{rll} \dfrac{x}{5+x} &=& \dfrac{2}{3} &\quad \scriptsize \mid\; \cdot (5+x) \\[5pt] x &=&\dfrac{10}{3} + \dfrac{2}{3}x &\quad \scriptsize \mid\;-\dfrac{2}{3}x \\[5pt] \dfrac{1}{3}x&=& \dfrac{10}{3} &\quad \scriptsize \mid\;\cdot 3 \\[5pt] x &=& 10 \end{array}$

Es müssen also $10$ grüne Kugeln hinzugefügt werden.

Lineare Algebra/Analytische Geometrie - Niveau 1

3.1

Damit es sich um ein Parallelogramm handelt, müssen alle gegenüberliegenden Seiten parallel zueinander sein.

$\begin{array}[t]{rll} \overrightarrow{AB} &=& \pmatrix{-2\\3\\1} \\[5pt] \overrightarrow{DC} &=& \pmatrix{-2\\3\\1} \\[5pt] \end{array}$

$\begin{array}[t]{rll} \overrightarrow{AD} &=& \pmatrix{1\\-3\\4} \\[5pt] \overrightarrow{BC} &=& \pmatrix{1\\-3\\4} \\[5pt] \end{array}$

Wegen $\overrightarrow{AB} = \overrightarrow{DC}$ und $\overrightarrow{AD} = \overrightarrow{BC}$ ist das Viereck $ABCD$ folglich ein Parallelogramm.

Das Viereck $ABCD$ ist genau dann ein Rechteck, wenn alle vier Innenwinkel rechte Winkel sind.

Es gilt:

$\begin{array}[t]{rll} \overrightarrow{AB} \circ \overrightarrow{AD} &=& \pmatrix{-2\\3\\1} \circ \pmatrix{1\\-3\\4} \\[5pt] &=& -2\cdot 1 +3\cdot (-3) + 1\cdot 4 \\[5pt] &=& -7 \\[5pt] &\neq& 0 \end{array}$

Die beiden Vektoren $\overrightarrow{AB}$ und $\overrightarrow{AD}$ sind also nicht orthogonal zueinander und die zugehörigen Seiten schließen folglich keinen rechten Winkel ein. Es kann sich daher nicht um ein Rechteck handeln.

Insgesamt handelt es sich bei $ABCD$ also um ein Parallelogramm, aber nicht um ein Rechteck.

3.2

Für den Mittelpunkt $M$ der Diagonalen $\overline{AC}$ gilt:

$\begin{array}[t]{rll} \overrightarrow{OM} &=& \dfrac{1}{2}\cdot \left(\overrightarrow{OA} + \overrightarrow{OC} \right) \\[5pt] &=& \dfrac{1}{2}\cdot \left(\pmatrix{5\\7\\2} + \pmatrix{4\\7\\7} \right) \\[5pt] &=& \pmatrix{4,5\\7\\4,5} \\[5pt] \end{array}$

Der Mittelpunkt der Diagonalen ist also $M\left(4,5\mid 7\mid 4,5 \right).$

Lineare Algebra/Analytische Geometrie - Niveau 2

Die Strecke $\overline{AB}$ liegt auf folgender Geraden:

$\begin{array}[t]{rll} h: \, \overrightarrow{x}&=& \overrightarrow{OA} + s\cdot \overrightarrow{AB} \\[5pt] &=& \pmatrix{-6\\8\\1} + s\cdot \pmatrix{3\\0\\-6 } \end{array}$

Gleichsetzen der beiden Geradengleichungen liefert:

Rechenweg anzeigen

$\pmatrix{-5\\6\\0} = r\cdot \pmatrix{2\\-3\\1} -s\cdot \pmatrix{3\\0\\-6 }$

Daraus ergibt sich folgendes Gleichungssystem:

$\begin{array}{lrll} \text{I:}\quad&-5&=& 2r-3s \\ \text{II:}\quad&6&=& -3r -0s \\ \text{III:}\quad&0&=& 1r +6s \\ \end{array}$

Aus der zweiten Gleichung folgt für $r:$

$\begin{array}[t]{rll} 6 &=& -3r &\quad \scriptsize \mid\; :(-3)\\[5pt] -2 &=& r \end{array}$

Einsetzen in die erste Gleichung liefert:

$\begin{array}[t]{rll} -5 &=& 2r-3s &\quad \scriptsize \mid\; r=-2 \\[5pt] -5 &=& 2\cdot (-2) -3s \\[5pt] -5 &=& -4 -3s &\quad \scriptsize \mid\;+4 \\[5pt] -1 &=& -3s &\quad \scriptsize \mid\;: (-3) \\[5pt] \dfrac{1}{3} &=& s \end{array}$

Einsetzen der beiden Lösungen in die dritte Gleichung ergibt nun:

$\begin{array}[t]{rll} 0 &=& 1r +6s \\[5pt] 0 &=& -2 + 6\cdot \dfrac{1}{3} \\[5pt] 0 &=& 0 \end{array}$

Die Lösung $r=-2$ und $s= \dfrac{1}{3}$ erfüllt also das Gleichungssystem. Somit schneiden sich die Geraden $g$ und $h.$

Wegen $0\leq s \leq 1,$ liegt der Schnittpunkt auf der Strecke $\overline{AB}.$