B1 - Analytische Geometrie
1.
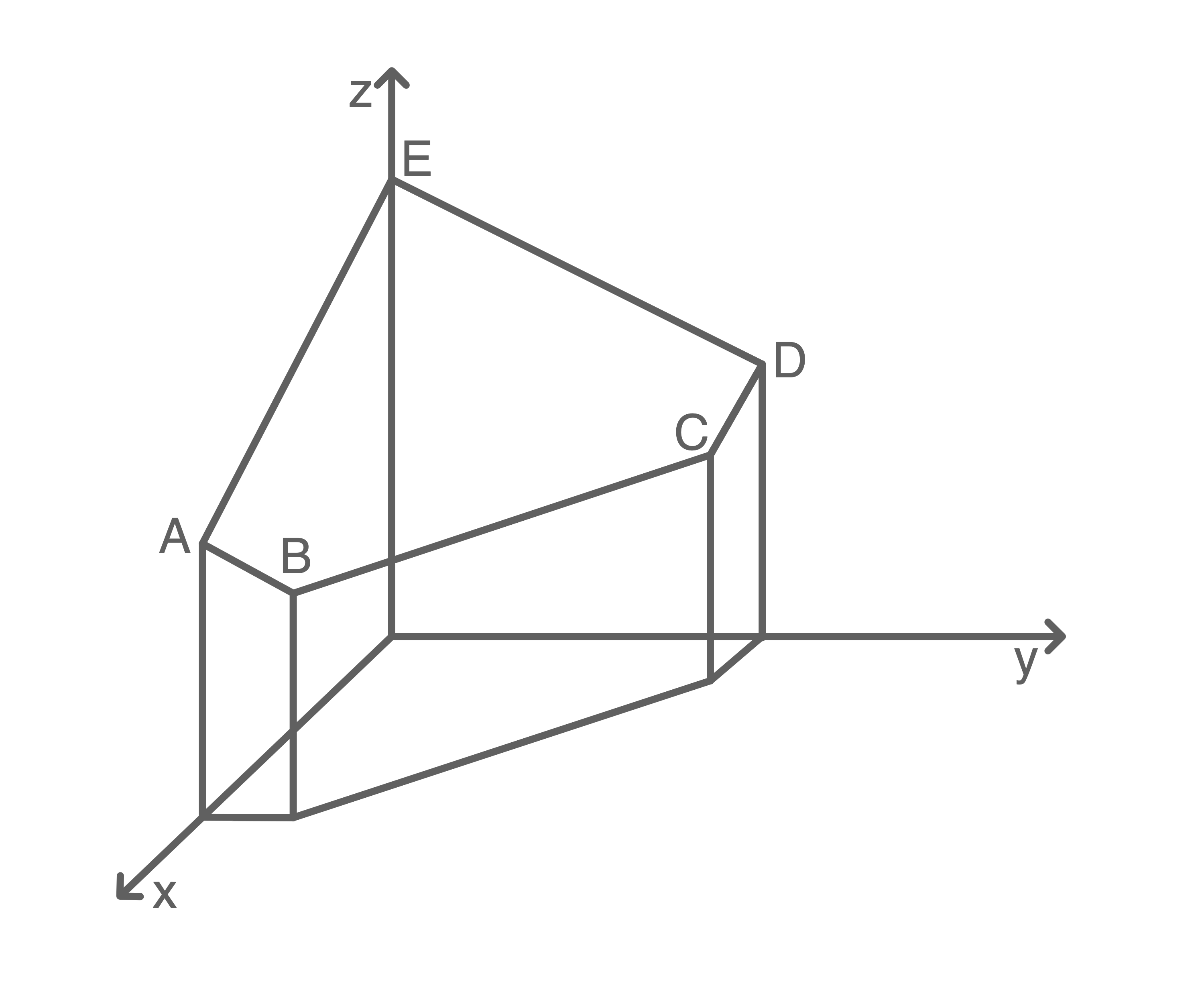
Zwischen zwei Wandseiten eines Wohnhauses, die in der  - bzw.
- bzw.  -Ebene liegen, soll ein symmetrischer Anbau in Glasbauweise als Wintergarten errichtet werden.
Der Boden des Wintergartens liegt in der
-Ebene liegen, soll ein symmetrischer Anbau in Glasbauweise als Wintergarten errichtet werden.
Der Boden des Wintergartens liegt in der  -Ebene. Das ebene Dach wird durch die Punkte
-Ebene. Das ebene Dach wird durch die Punkte  ,
,  ,
,  ,
,  und
und  begrenzt.
Gegeben sind die Punkte
begrenzt.
Gegeben sind die Punkte  ,
,  ,
,  und
und  . Hierbei entspricht eine Längeneinheit einem Meter.
Der Punkt
. Hierbei entspricht eine Längeneinheit einem Meter.
Der Punkt  liegt in der
liegt in der  -Ebene, die Strecke
-Ebene, die Strecke  verläuft parallel zur Dachkante
verläuft parallel zur Dachkante  .
.
1.1
Gib die Koordinaten des Punktes  an und erkläre deine Vorgehensweise.
an und erkläre deine Vorgehensweise.
(3 BE)
1.2
Bestimme eine Parametergleichung und eine Koordinatengleichung der Ebene  , in der die Dachfläche
, in der die Dachfläche  liegt.
liegt.
 zur Kontrolle:
zur Kontrolle:  ist eine mögliche Koordinatengleichung von
ist eine mögliche Koordinatengleichung von 
![\(]\)](https://www.schullv.de/resources/formulas/cfae0d4248f7142f7b17f826cd7a519280e312577690e957830d23dcf35a3fff_light.svg)
(5 BE)
1.3
Damit Schnee gut abrutschen kann, sollte der Neigungswinkel der Dachfläche gegen die Grundfläche mindestens  betragen. Prüfe rechnerisch, ob diese Bedingung erfüllt ist.
betragen. Prüfe rechnerisch, ob diese Bedingung erfüllt ist.
(3 BE)
2.
Zur Beschattung wird in den Sommermonaten ein zur Dachfläche  paralleles Dreieckssegel oberhalb der Dachfläche gespannt. Das Segel liegt in der Ebene
paralleles Dreieckssegel oberhalb der Dachfläche gespannt. Das Segel liegt in der Ebene  .
Bestätige rechnerisch, dass der Abstand des Segels zur Dachfläche
.
Bestätige rechnerisch, dass der Abstand des Segels zur Dachfläche  ca.
ca.  beträgt.
beträgt.
(6 BE)
3.
Zur Stabilisierung der Dachfläche werden der Punkt  mit dem Mittelpunkt
mit dem Mittelpunkt  der Dachkante
der Dachkante  sowie der Punkt
sowie der Punkt  mit dem Punkt
mit dem Punkt  durch Streben verbunden, wobei
durch Streben verbunden, wobei  ist.
ist.
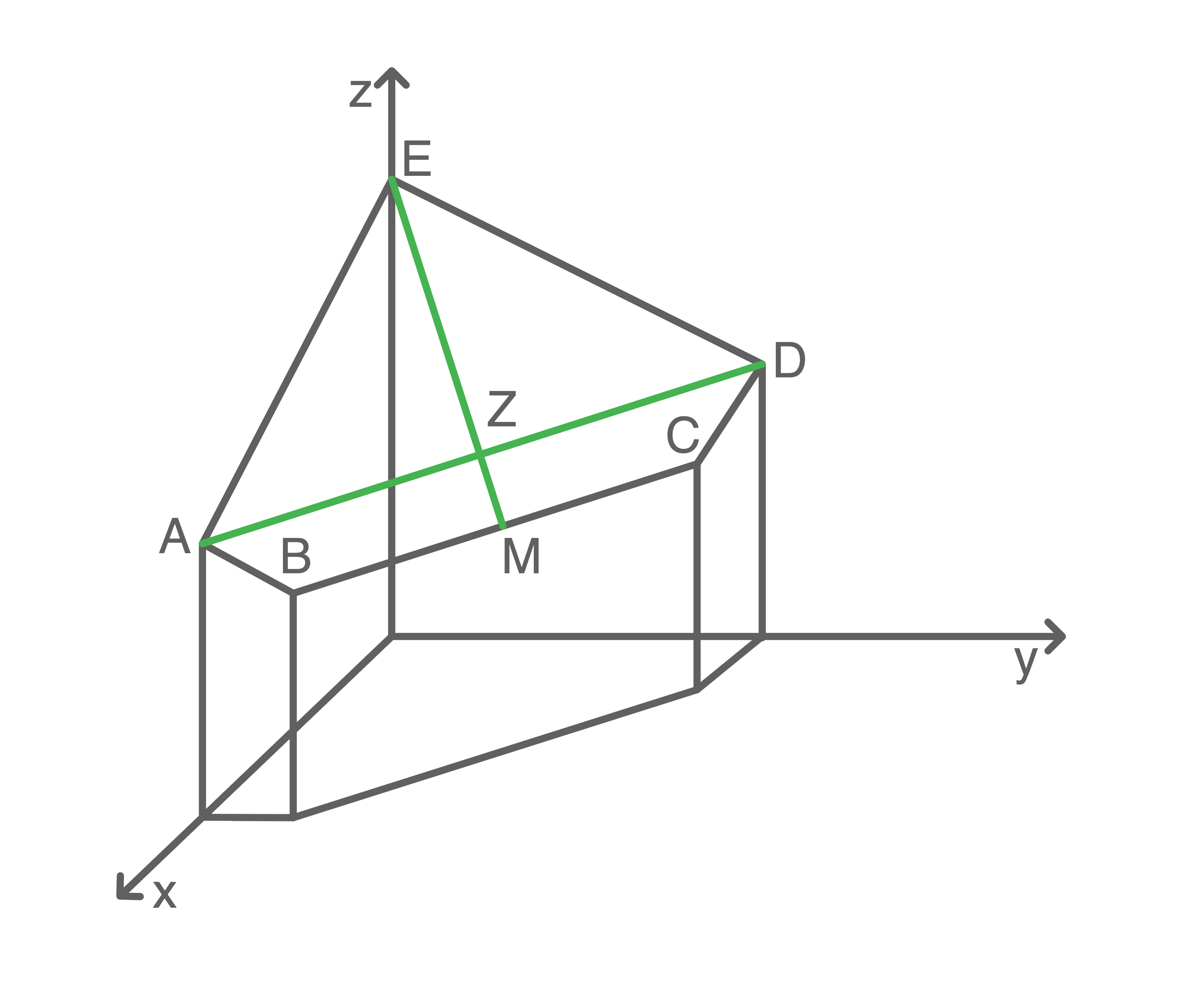
3.1
Zeige, dass der Punkt  der Schnittpunkt der beiden Streben
der Schnittpunkt der beiden Streben  und
und  ist.
Zeichne die beiden Streben und den Punkt
ist.
Zeichne die beiden Streben und den Punkt  in das Material.
in das Material.
(5 BE)
3.2
Das Dach des Wintergartens soll eine besondere Verglasung erhalten; dazu muss der Materialverbrauch ermittelt werden.
Erkläre die Bedeutung der Zeilen 1 bis 4 im Kasten jeweils im Sachzusammenhang.
Bestimme anschließend den restlichen Inhalt der Dachfläche und gib den insgesamt benötigten Materialverbrauch in Quadratmetern an.




(8 BE)
1.
1.1
Da die Strecke  laut Aufgabenstellung parallel zur Dachkante
laut Aufgabenstellung parallel zur Dachkante  verläuft, liegt der Punkt
verläuft, liegt der Punkt  auf derselben Höhe wie der Punkt
auf derselben Höhe wie der Punkt  . Folglich muss die
. Folglich muss die  -Koordinate von
-Koordinate von  gleich
gleich  sein.
Da der Punkt
sein.
Da der Punkt  in der
in der  -Ebene und Punkt
-Ebene und Punkt  in der
in der  -Ebene liegt, müssen aus Symmetriegründen die
-Ebene liegt, müssen aus Symmetriegründen die  - und
- und  -Koordinaten der Punkte vertauscht sein. Somit ergibt sich der Punkt
-Koordinaten der Punkte vertauscht sein. Somit ergibt sich der Punkt  zu
zu 
1.2
Parametergleichung ermitteln
Koordinatengleichung bestimmen
Allgemeine Koordinatenform:
 Ein Normalenvektor
Ein Normalenvektor  der Ebene
der Ebene  ergibt sich beispielsweise durch:
ergibt sich beispielsweise durch:
![\(\begin{array}[t]{rll}
\overrightarrow{n_D} &=& \overrightarrow{EA} \times \overrightarrow{ED} \\[5pt]
&=& \pmatrix{4\\0\\-2}\times\pmatrix{0\\4\\-2} \\[5pt]
&=& \pmatrix{0\cdot (-2)-(-2)\cdot 4\\(-2)\cdot 0-(-2)\cdot 4\\4\cdot 4-0\cdot 0} \\[5pt]
&=& \pmatrix{8\\8\\16} \\[5pt]
&=& 8\cdot \pmatrix{1\\1\\2} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/20a103bf66b265a082a4250835ae3b89585f202a9b7567de4cd1311a842c3734_light.svg) Ein Normalenvektor von
Ein Normalenvektor von  ist somit beispielsweise gegeben durch
ist somit beispielsweise gegeben durch  Durch Einsetzen von
Durch Einsetzen von  und
und  in die allgemeine Koordinatenform folgt:
in die allgemeine Koordinatenform folgt:
![\(\begin{array}[t]{rll}
1\cdot 0+ 1 \cdot 0 + 2 \cdot 5 &=& d \\[5pt]
10 &=& d
\end{array}\)](https://www.schullv.de/resources/formulas/ccaa71a9f13007cae938ee9e2eca093c52a61578bef3de67068305be9c6cc443_light.svg) Eine Koordinatengleichung von
Eine Koordinatengleichung von  lautet somit:
lautet somit:

1.3
Der Neigungswinkel des Daches entspricht dem Winkel  zwischen den Normalenvektoren
zwischen den Normalenvektoren  der
der  -Ebene und den Normalenvektoren
-Ebene und den Normalenvektoren  der Dachebene
der Dachebene 
![\(\begin{array}[t]{rll}
\cos(\alpha) &=&\dfrac{ \mid \overrightarrow{n_{xy}} \cdot \overrightarrow{n_{D}} \mid} {\mid \overrightarrow{n_{xy}} \mid \cdot \mid \overrightarrow{n_{D}} \mid} \\[5pt]
\cos(\alpha) &=& \dfrac{ \left \vert \pmatrix{0\\0\\1} \circ \pmatrix{1\\1\\2}\right \vert}{ \left \vert\pmatrix{0\\0\\1} \right \vert \cdot \left \vert \pmatrix{1\\1\\2}\right \vert} \\[5pt]
\cos(\alpha)&=& \dfrac{\mid 0\cdot 1+0\cdot 1+1\cdot 2\mid}{\sqrt{1}\cdot \sqrt{6}} \\[5pt]
\cos(\alpha)&=& \dfrac{2}{\sqrt{6}} &\quad \scriptsize \mid \arccos \\[15pt]
\alpha &=& \cos^{-1}\left(\dfrac{2}{\sqrt{6}}\right) \\[5pt]
\alpha&\approx& 35,26\,^{\circ}
\end{array}\)](https://www.schullv.de/resources/formulas/a2aa8e951cf6edc7b16689a8fd048f6026a3d02c21f3a2ad1ad77e78749497ec_light.svg) Der Neigungswinkel beträgt somit
Der Neigungswinkel beträgt somit  und das Dach erfüllt somit die Bedingung.
und das Dach erfüllt somit die Bedingung.
2.
Da  laut Aufgabenstellung parallel zu
laut Aufgabenstellung parallel zu  ist, gilt:
ist, gilt:
![\(\begin{array}[t]{rll}
d(E_1,E_2)&=& \left \vert \dfrac{ \overrightarrow{n} \circ (\overrightarrow{OP_{E_1}} - \overrightarrow{OP_{E_2}})}{ \vert \overrightarrow{n} \vert } \right \vert
\end{array}\)](https://www.schullv.de/resources/formulas/192a886559233e26cc4620c5fb90ea436176e8a0cad02c02423a47d0cb33a385_light.svg) Hierbei ist
Hierbei ist  ein Normalenvektor der beiden Ebenen und
ein Normalenvektor der beiden Ebenen und  und
und  sind beliebige Punkte in
sind beliebige Punkte in  und
und  Aus Aufgabenteil 1.2 können der Normalenvektor
Aus Aufgabenteil 1.2 können der Normalenvektor  und der Punkt
und der Punkt  aus der Ebene
aus der Ebene  übernommen werden.
Die Koordinaten eines Punkt aus der Ebene
übernommen werden.
Die Koordinaten eines Punkt aus der Ebene  können durch Einsetzen beliebiger
können durch Einsetzen beliebiger  - und
- und  -Koordinaten in die Koordinatengleichung von
-Koordinaten in die Koordinatengleichung von  ermittelt werden. Mit
ermittelt werden. Mit  und
und  folgt:
folgt:
![\(\begin{array}[t]{rll}
E_2: 1\cdot 0+1\cdot 0+2\cdot z&=& 10,2 &\quad \scriptsize \mid\; :2 \\[5pt]
z &=& 5,1
\end{array}\)](https://www.schullv.de/resources/formulas/64bee0046736a57a324f49d3bc7dcb362ecfdec8f6d974ff576ce8080a01b11f_light.svg) Der Punkt
Der Punkt  liegt somit in der Ebene
liegt somit in der Ebene  Es folgt also:
Der Abstand zwischen
Es folgt also:
Der Abstand zwischen  und
und  beträgt somit etwa
beträgt somit etwa 
3.
3.1
Es gilt:
![\(\begin{array}[t]{rll}
g_{\overline{A D}}: \overrightarrow{ x }&=& \overrightarrow{OD}+r\cdot \overrightarrow{AD}&\\[5pt]
&=& \left(\begin{array}{l}0 \\ 4 \\ 3\end{array}\right)+r \cdot\left(\begin{array}{c}-4 \\ 4 \\ 0\end{array}\right)
\end{array}\)](https://www.schullv.de/resources/formulas/41d39cdae2a12b504f2cebfbbcb7a01a9cbfbb3d79db3f038df48801d29030f5_light.svg)
![\(\begin{array}[t]{rll}
g_{\overline{ EM }}: \overrightarrow{ x }&=& \overrightarrow{OD} +s\cdot \overrightarrow{EM} & \\[5pt]
&=&\left(\begin{array}{l}0 \\ 0 \\ 5\end{array}\right)+ s \cdot\left(\begin{array}{c}2,5 \\ 2,5 \\ -2,5\end{array}\right)
\end{array}\)](https://www.schullv.de/resources/formulas/ac41145bfffaada630d254532d32361a8ba24e86b085b528ec30e8d48774c652_light.svg) Koordinaten von
Koordinaten von  in
in  einsetzen:
einsetzen:
 Aus der ersten Zeile folgt:
Aus der ersten Zeile folgt:
![\(\begin{array}[t]{rll}
2&=& -4\cdot r &\quad \scriptsize \mid\; :(-4) \\[5pt]
-\dfrac{1}{2}&=& r
\end{array}\)](https://www.schullv.de/resources/formulas/394e2768d3ff031b4baad69b060144efe2ff6347145a9bc4721311716b1b04fa_light.svg) Durch Einsetzen von
Durch Einsetzen von  in die zweite und dritte Zeile folgt:
in die zweite und dritte Zeile folgt:

 Koordinaten von
Koordinaten von  in
in  einsetzen:
einsetzen:
 Aus der ersten und zweiten Zeile ergibt sich:
Aus der ersten und zweiten Zeile ergibt sich:
![\(\begin{array}[t]{rll}
2&=& 2,5\cdot s &\quad \scriptsize \mid\; :2,5 \\[5pt]
\dfrac{4}{5} &=& s
\end{array}\)](https://www.schullv.de/resources/formulas/555dca53508f8003d48b0e61557ef113ed4e5a1a555c1f0354efac764b69c664_light.svg) Durch Einsetzen von
Durch Einsetzen von  in die dritte Reihe folgt:
in die dritte Reihe folgt:
 Somit liegt der Punkt
Somit liegt der Punkt  auf beiden Geraden und bildet folglich den Schnittpunkt der beiden Streben.
auf beiden Geraden und bildet folglich den Schnittpunkt der beiden Streben.

3.2
Bedeutung erklären

- Die Vektoren
und
werden angegeben. Diese entsprechen den Richtungen der beiden Streben.
- Da das Skalarprodukt aus den Vektoren null ergibt, stehen die beiden Streben folglich senkrecht aufeinander.
- In diesem Schritt wird der Vektor
bestimmt.
- Es wird der Flächeninhalt des dreieckigen Dachteils
mit
als Grundseite und
als Höhe berechnet. Der Inhalt beträgt ca.
1.
1.1
Da die Strecke  laut Aufgabenstellung parallel zur Dachkante
laut Aufgabenstellung parallel zur Dachkante  verläuft, liegt der Punkt
verläuft, liegt der Punkt  auf derselben Höhe wie der Punkt
auf derselben Höhe wie der Punkt  . Folglich muss die
. Folglich muss die  -Koordinate von
-Koordinate von  gleich
gleich  sein.
Da der Punkt
sein.
Da der Punkt  in der
in der  - und Punkt
- und Punkt  in der
in der  -Ebene liegt, müssen aus Symmetriegründen die
-Ebene liegt, müssen aus Symmetriegründen die  - und
- und  -Koordinaten der Punkte vertauscht sein. Somit ergibt sich der Punkt
-Koordinaten der Punkte vertauscht sein. Somit ergibt sich der Punkt  zu
zu 
1.2
Parametergleichung ermitteln
Koordinatengleichung bestimmen
Allgemeine Koordinatenform:
 Ein Normalenvektor
Ein Normalenvektor  der Ebene
der Ebene  ergibt sich beispielsweise durch:
ergibt sich beispielsweise durch:
![\(\begin{array}[t]{rll}
\overrightarrow{n_D} &=& \overrightarrow{EA} \times \overrightarrow{ED} \\[5pt]
&=& \pmatrix{4\\0\\-2}\times\pmatrix{0\\4\\-2} \\[5pt]
&=& \pmatrix{0\cdot (-2)-(-2)\cdot 4\\(-2)\cdot 0-(-2)\cdot 4\\4\cdot 4-0\cdot 0} \\[5pt]
&=& \pmatrix{8\\8\\16} \\[5pt]
&=& 8\cdot \pmatrix{1\\1\\2} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/20a103bf66b265a082a4250835ae3b89585f202a9b7567de4cd1311a842c3734_light.svg) Ein Normalenvektor von
Ein Normalenvektor von  ist somit beispielsweise gegeben durch
ist somit beispielsweise gegeben durch  Durch Einsetzen von
Durch Einsetzen von  und
und  in die allgemeine Koordinatenform folgt:
in die allgemeine Koordinatenform folgt:
![\(\begin{array}[t]{rll}
1\cdot 0+ 1 \cdot 0 + 2 \cdot 5 &=& d \\[5pt]
10 &=& d
\end{array}\)](https://www.schullv.de/resources/formulas/ccaa71a9f13007cae938ee9e2eca093c52a61578bef3de67068305be9c6cc443_light.svg) Eine Koordinatengleichung von
Eine Koordinatengleichung von  lautet somit:
lautet somit:

1.3
Der Neigungswinkel des Daches entspricht dem Winkel  zwischen den Normalenvektoren
zwischen den Normalenvektoren  der
der  -Ebene und den Normalenvektoren
-Ebene und den Normalenvektoren  der Dachebene
der Dachebene 
![\(\begin{array}[t]{rll}
\cos(\alpha) &=&\dfrac{ \mid \overrightarrow{n_{xy}} \cdot \overrightarrow{n_{D}} \mid} {\mid \overrightarrow{n_{xy}} \mid \cdot \mid \overrightarrow{n_{D}} \mid} \\[5pt]
\cos(\alpha) &=& \dfrac{ \left \vert \pmatrix{0\\0\\1} \circ \pmatrix{1\\1\\2}\right \vert}{ \left \vert\pmatrix{0\\0\\1} \right \vert \cdot \left \vert \pmatrix{1\\1\\2}\right \vert} \\[5pt]
\cos(\alpha)&=& \dfrac{\mid 0\cdot 1+0\cdot 1+1\cdot 2\mid}{\sqrt{1}\cdot \sqrt{6}} \\[5pt]
\cos(\alpha)&=& \dfrac{2}{\sqrt{6}} &\quad \scriptsize \mid \arccos \\[15pt]
\alpha &=& \cos^{-1}\left(\dfrac{2}{\sqrt{6}}\right) \\[5pt]
\alpha&\approx& 35,26\,^{\circ}
\end{array}\)](https://www.schullv.de/resources/formulas/a2aa8e951cf6edc7b16689a8fd048f6026a3d02c21f3a2ad1ad77e78749497ec_light.svg) Der Neigungswinkel beträgt somit
Der Neigungswinkel beträgt somit  und das Dach erfüllt somit die Bedingung.
und das Dach erfüllt somit die Bedingung.
2.
Da  laut Aufgabenstellung parallel zu
laut Aufgabenstellung parallel zu  ist, gilt:
ist, gilt:
![\(\begin{array}[t]{rll}
d(E_1,E_2)&=& \left \vert \dfrac{ \overrightarrow{n} \circ (\overrightarrow{OP_{E_1}} - \overrightarrow{OP_{E_2}})}{ \vert \overrightarrow{n} \vert } \right \vert
\end{array}\)](https://www.schullv.de/resources/formulas/192a886559233e26cc4620c5fb90ea436176e8a0cad02c02423a47d0cb33a385_light.svg) Hierbei ist
Hierbei ist  ein Normalenvektor der beiden Ebenen und
ein Normalenvektor der beiden Ebenen und  und
und  sind beliebige Punkte in
sind beliebige Punkte in  und
und  Aus Aufgabenteil 1.2 können der Normalenvektor
Aus Aufgabenteil 1.2 können der Normalenvektor  und der Punkt
und der Punkt  aus der Ebene
aus der Ebene  übernommen werden.
Die Koordinaten eines Punkt aus der Ebene
übernommen werden.
Die Koordinaten eines Punkt aus der Ebene  können durch Einsetzen beliebiger
können durch Einsetzen beliebiger  - und
- und  -Koordinaten in die Koordinatengleichung von
-Koordinaten in die Koordinatengleichung von  ermittelt werden. Mit
ermittelt werden. Mit  und
und  folgt:
folgt:
![\(\begin{array}[t]{rll}
E_2: 1\cdot 0+1\cdot 0+2\cdot z&=& 10,2 &\quad \scriptsize \mid\; :2 \\[5pt]
z &=& 5,1
\end{array}\)](https://www.schullv.de/resources/formulas/64bee0046736a57a324f49d3bc7dcb362ecfdec8f6d974ff576ce8080a01b11f_light.svg) Der Punkt
Der Punkt  liegt somit in der Ebene
liegt somit in der Ebene  Es folgt also:
Der Abstand zwischen
Es folgt also:
Der Abstand zwischen  und
und  beträgt somit etwa
beträgt somit etwa 
3.
3.1
Es gilt:
![\(\begin{array}[t]{rll}
g_{\overline{A D}}: \overrightarrow{ x }&=& \overrightarrow{OD}+r\cdot \overrightarrow{AD}&\\[5pt]
&=& \left(\begin{array}{l}0 \\ 4 \\ 3\end{array}\right)+r \cdot\left(\begin{array}{c}-4 \\ 4 \\ 0\end{array}\right)
\end{array}\)](https://www.schullv.de/resources/formulas/41d39cdae2a12b504f2cebfbbcb7a01a9cbfbb3d79db3f038df48801d29030f5_light.svg)
![\(\begin{array}[t]{rll}
g_{\overline{ EM }}: \overrightarrow{ x }&=& \overrightarrow{OD} +s\cdot \overrightarrow{EM} & \\[5pt]
&=&\left(\begin{array}{l}0 \\ 0 \\ 5\end{array}\right)+ s \cdot\left(\begin{array}{c}2,5 \\ 2,5 \\ -2,5\end{array}\right)
\end{array}\)](https://www.schullv.de/resources/formulas/ac41145bfffaada630d254532d32361a8ba24e86b085b528ec30e8d48774c652_light.svg) Koordinaten von
Koordinaten von  in
in  einsetzen:
einsetzen:
 Aus der ersten Zeile folgt:
Aus der ersten Zeile folgt:
![\(\begin{array}[t]{rll}
2&=& -4\cdot r &\quad \scriptsize \mid\; :(-4) \\[5pt]
-\dfrac{1}{2}&=& r
\end{array}\)](https://www.schullv.de/resources/formulas/394e2768d3ff031b4baad69b060144efe2ff6347145a9bc4721311716b1b04fa_light.svg) Durch Einsetzen von
Durch Einsetzen von  in die zweite und dritte Zeile folgt:
in die zweite und dritte Zeile folgt:

 Koordinaten von
Koordinaten von  in
in  einsetzen:
einsetzen:
 Aus der ersten und zweiten Zeile ergibt sich:
Aus der ersten und zweiten Zeile ergibt sich:
![\(\begin{array}[t]{rll}
2&=& 2,5\cdot s &\quad \scriptsize \mid\; :2,5 \\[5pt]
\dfrac{4}{5} &=& s
\end{array}\)](https://www.schullv.de/resources/formulas/555dca53508f8003d48b0e61557ef113ed4e5a1a555c1f0354efac764b69c664_light.svg) Durch Einsetzen von
Durch Einsetzen von  in die dritte Reihe folgt:
in die dritte Reihe folgt:
 Somit liegt der Punkt
Somit liegt der Punkt  auf beiden Geraden und bildet folglich den Schnittpunkt der beiden Streben.
auf beiden Geraden und bildet folglich den Schnittpunkt der beiden Streben.


3.2
Bedeutung erklären

- Die Vektoren
und
werden angegeben. Diese entsprechen den Richtungen der beiden Streben.
- Da das Skalarprodukt aus den Vektoren null ergibt, stehen die beiden Streben folglich senkrecht aufeinander.
- In diesem Schritt wird der Vektor
bestimmt.
- Es wird der Flächeninhalt des dreieckigen Dachteils
mit
als Grundseite und
als Höhe berechnet. Der Inhalt beträgt ca.