B2 - Analytische Geometrie

Ein alter Kirchturm (ähnlich dem Kirchturm in Unterloibach (Österreich), siehe Abbildung 1) hat die Form eines Quaders mit quadratischer Grundfläche und einer aufgesetzten Pyramide.

Die Spitze der Pyramide befindet sich senkrecht über dem Mittelpunkt ihrer Grundfläche.

Eine gelbe Kirche mit spitzem Turm vor blauem Himmel.

Abbildung 1

Die Kanten der Grundfläche des betrachteten Kirchturms sind $6\,\text{m}$ lang, die Höhe des Pyramidendachs beträgt ebenfalls $6\,\text{m}$ . Insgesamt ist der Turm $18\,\text{m}$ hoch.

1.1

Zeichne den Kirchturm in das Koordinatensystem in Abbildung 2 und beschrifte die Zeichnung gemäß folgenden Vorgaben:

Die Eckpunkte der Grundfläche des Kirchturms sollen mit $A$ , $B$ , $C$ und $D$ bezeichnet werden.

Der Eckpunkt $A$ liegt im Koordinatenursprung. Der Eckpunkt $B$ soll auf der positiven $x$ -Achse und der Eckpunkt $D$ auf der positiven $y$ -Achse liegen.

Die Eckpunkte des Bodens des Pyramidendachs sollen entsprechend mit $E, F, G$ und $H$ bezeichnet werden, wobei der Eckpunkt $E$ über dem Eckpunkt $A$ liegt. Die Spitze des Dachs liegt im Punkt $S(3\mid 3\mid 18).$

Gib die Koordinaten der Eckpunkte $C$ und $F$ des Turms an.

Koordinatensystem Hessen Mathe Abi 2017 Kirchturm

Abbildung 2

(4 BE)

1.2

Der Kirchturm soll saniert werden. Dazu wird unter anderem das Dach neu eingedeckt.

Berechne den Flächeninhalt der Dachfläche.

(3 BE)

Zur Stabilisierung des Dachs sollen im Dachraum zwei Stützbalken eingezogen werden, deren Dicke bei den folgenden Betrachtungen vernachlässigt wird.

2.1

Der erste Stützbalken soll die Mitte $M(3\mid 0\mid 12)$ der Dachbodenkante $\overline{EF}$ mit der gegenüberliegenden Dachfläche mit den Eckpunkten $G(6\mid6\mid12),$ $H(0\mid6\mid12)$ und $S(3\mid3\mid18)$ verbinden und orthogonal zur Dachfläche $GHS$ verlaufen.

2.1.1

Gib eine Parameterform der Ebene $E_{GHS},$ in der die Dachfläche mit den Eckpunkten $G, H$ und $S$ liegt, an und bestimme eine zugehörige Koordinatengleichung.

$\big[$ Zur Kontrolle: Eine mögliche Koordinatengleichung lautet $E_{GHS}: \; 2y+z = 24. \big]$

(5 BE)

2.1.2

Erläutere die Zeilen $\text{(1)}$ bis $\text{(4)}$ im untenstehenden Kasten im Sachzusammenhang.

Gib die fehlende Rechnung in Zeile $\text{(3)}$ an und bestimme das Ergebnis in Zeile $\text{(4)}.$

$\boldsymbol{\text{(1)}}$

$g:\; \overrightarrow{x} = \pmatrix{3\\0\\12}+ r\cdot \pmatrix{0\\2\\1}$

$\boldsymbol{\text{(2)}}$

$\begin{array}[t]{rll} 4r+12+r&=&24 \\[5pt] \Leftrightarrow r&=& \dfrac{12}{5} \end{array}$

$\boldsymbol{\text{(3)}}$

$... \, \Rightarrow\, P\left( 3 \,\bigg \vert \, \dfrac{24}{5} \,\bigg \vert \, \dfrac{72}{5}\right)$

$\boldsymbol{\text{(4)}}$

$\left| \pmatrix{0\\ \dfrac{24}{5} \\ \dfrac{12}{5}}\right|\; \approx \; ...$

(8 BE)

2.2

Der zweite Stützbalken soll den Eckpunkt $H$ des Bodens des Pyramidendachs mit der Dachkante $\overline{FS}$ verbinden und orthogonal zur Dachkante $\overline{FS}$ verlaufen.

Ein Richtungsvektor der Geraden $k,$ auf der der zweite Stützbalken liegt, ist $\overrightarrow{u} = \pmatrix{1\\-1\\1}.$

Prüfe, ob sich die beiden Stützbalken schneiden.

(5 BE)

Zum jährlichen Kirchweihfest wird immer ein sogenannter Kirmesbaum aufgestellt, dessen unteres Ende im Punkt $Q(24\mid 4\mid 0)$ befestigt ist. In diesem Jahr ist der Kirmesbaum $10\,\text{m}$ hoch.

Zu einem bestimmten Zeitpunkt fallen die Sonnenstrahlen in Richtung des Vektors $\overrightarrow{v} = \pmatrix{-9\\-1\\-1}$ ein.

Begründe, dass der Schattenpunkt der Kirmesbaumspitze zu diesem Zeitpunkt auf eine Seitenfläche des Turms trifft, und gib die Eckpunkte dieser Seitenfläche sowie die Koordinaten des Schattenpunkts der Kirmesbaumspitze an.

(5 BE)

1.1

Kirchturm einzeichnen

Beginnend mit $A$ im Ursprung und mit Hilfe der in der Aufgabenstellung gegebenen Längenangaben folgt für den Kirchturm:

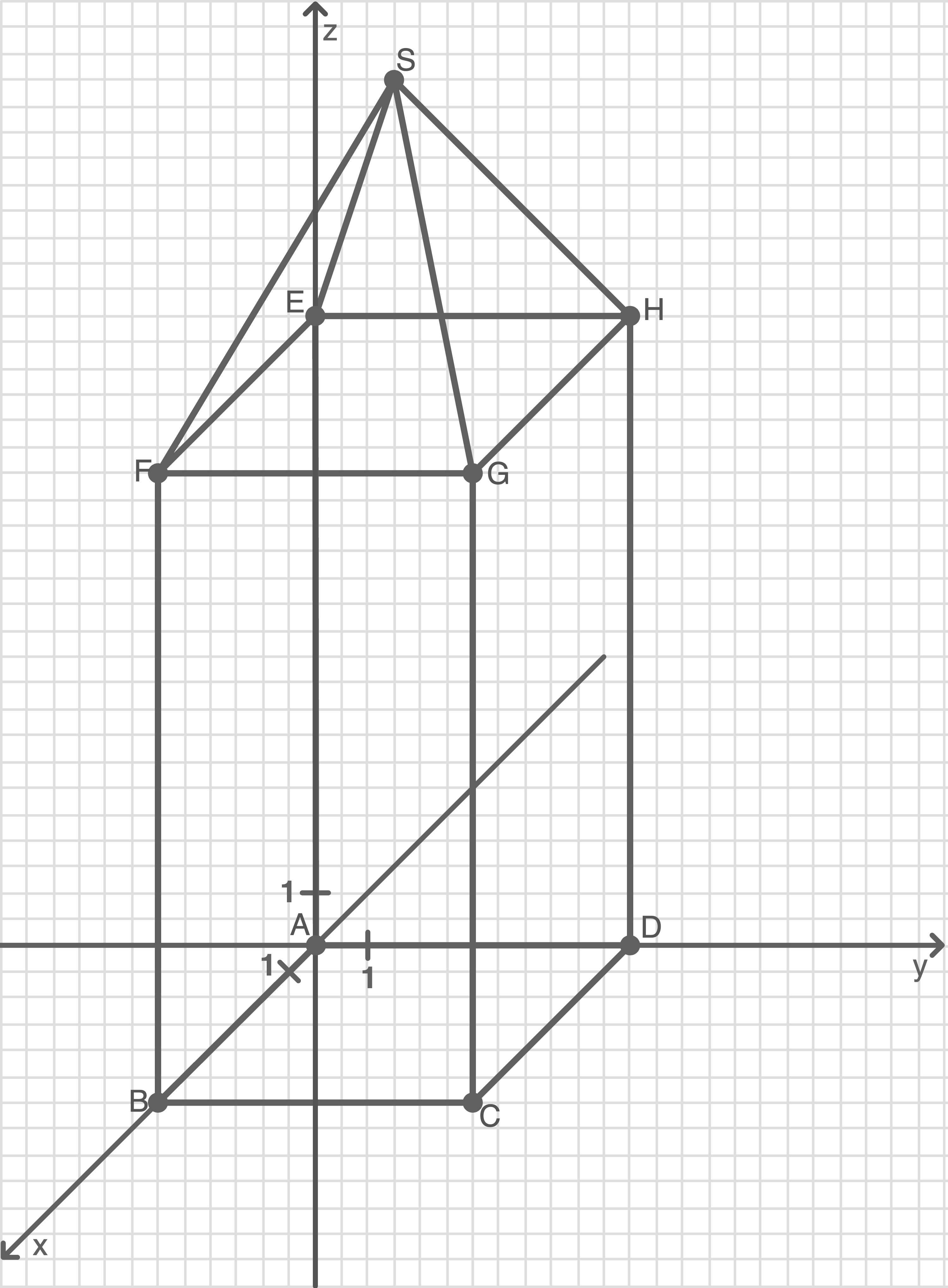Hessen Abi 2017 Kirchturm Koordinaten Eckpunkte

Koordinaten der Eckpunkte angeben

$C(6\mid6\mid 0)$

$F(6\mid 0\mid 12)$

1.2

Da das Dach eine regelmäßige vierseitige Pyramide ist, sind alle vier Seitenflächen gleichgroß und die Dachfläche ist das Vierfache des Flächeninhalts einer dieser Seitenflächen.

Für die Berechnung von zum Beispiel der Seitenfläche $EFS$ werden die Verbindungsvektoren $\overrightarrow{FE}$ und $\overrightarrow{FS}$ benötigt:

$\begin{array}[t]{rll} \overrightarrow{FE} &=& \pmatrix{0\\0\\12} - \pmatrix{6\\0\\12}& \\[5pt] &=& \pmatrix{-6\\0\\0} \end{array}$

$\begin{array}[t]{rll} \overrightarrow{FS}&=& \pmatrix{3\\3\\18} - \pmatrix{6\\0\\12}& \\[5pt] &=& \pmatrix{-3\\3\\6} \end{array}$

Für den Flächeninhalt folgt mit dem crossP-Befehl des CAS:

$\begin{array}[t]{rll} A_{EFS}&=& \dfrac{1}{2} \cdot \left| \overrightarrow{FE}\times \overrightarrow{FS}\right| \\[5pt] &=& \dfrac{1}{2} \cdot \left| \pmatrix{-6\\0\\0} \times \pmatrix{-3\\3\\6}\right|\\[5pt] &=& 9\cdot \sqrt{5} \;[\text{m}^2]\\[5pt] \end{array}$

Mathematische Berechnung mit Kreuzprodukt und Norm in einer Software-Anwendung.

Die gesamte Dachfläche ergibt sich damit zu:

$\begin{array}[t]{rll} A_{\text{Dach}}&=& 4\cdot A_{EFS} & \\[5pt] &=& 4\cdot 9\cdot \sqrt{5}& \\[5pt] &\approx& 80,5 \;[\text{m}^2]& \\[5pt] \end{array}$

2.1.1

Parameterform angeben

$E_{GHS}:\; \overrightarrow{x} = \overrightarrow{OG} + s\cdot \overrightarrow{GS} + t\cdot \overrightarrow{GH}$

Vollständige Gleichung anzeigen

Koordinatengleichung bestimmen

Das Kreuzprodukt aus zwei Spannvektoren der Ebene liefert einen Normalenvektor:

$\begin{array}[t]{rll} \overrightarrow{n}_1&=& \overrightarrow{GS}\times \overrightarrow{GH} \\[5pt] &=& \pmatrix{-3\\-3\\6} \times \pmatrix{-6\\0\\0} \\[5pt] &=& \pmatrix{-3\cdot 0 - 6\cdot 0\\ 6\cdot (-6) - (-3)\cdot 0\\ (-3)\cdot 0 -(-3)\cdot (-6)}\\[5pt] &=& \pmatrix{0\\ -36 \\ -18} \\[5pt] &=& -18\cdot\pmatrix{0\\2\\1} \\[5pt] \end{array}$

Einsetzen des gekürzten Normalenvektors $\overrightarrow{n} = \pmatrix{0\\2\\1}$ sowie der Koordinaten von $G$ liefert nun:

$\begin{array}[t]{rll} d&=& n_1\cdot x +n_2\cdot y+n_3\cdot z \\[5pt] &=& 0\cdot 6 + 2\cdot 6 + 1\cdot 12 \\[5pt] &=& 24 \end{array}$

Eine Gleichung der Ebene $E_{GHS}$ in Koordinatenform lautet somit:

$E_{GHS}:\; 2\cdot y + z = 24$

Alternativer Lösungsweg:

Aus der zweiten Zeile der Parametergleichung von $E_{GHS}$ folgt:

$\begin{array}[t]{rll} y&=& 6-3\cdot t&\quad \scriptsize \mid\; -6 \\[5pt] y-6&=& -3\cdot t&\quad \scriptsize \mid\; :(-3) \\[5pt] \dfrac{1}{3}\cdot (6-y)&=& t \end{array}$

Damit ergibt sich nun:

$2y+z=24$

Rechenweg anzeigen

Eine Gleichung der Ebene $E_{GHS}$ in Koordinatenform lautet somit:

$E_{GHS}:\; 2\cdot y + z = 24$

2.1.2

Zeilen erläutern

$\text{(1)}$

$g$ ist die Parametergleichung einer Gerade, die $M$ als Stützpunkt und einen Normalenvektor der Ebene $E_{GHS}$ als Richtungsvektor besitzt. Die Gerade verläuft also orthogonal zur Ebene $GHS$ und enthält somit laut Aufgabenstellung den ersten Stützbalken.

$\text{(2)}$

Durch Einsetzen der Koordinaten der allgemeinen Punkte von $g$ in die Koordinatenform der Ebenengleichung von $E_{GHS}$ und auflösen nach $r$ wird hier der Parameterwert $r$ berechnet, für den sich die Gerade und die Dachebene schneiden.

$\text{(3)}$

Einsetzen des Wertes von $r$ aus Zeile $\text{(2)}$ in die Geradengleichung ergibt die Koordinaten des Punkts $P,$ in dem der Stützbalken auf die Dachfläche $GHS$ trifft.

$\text{(4)}$

Durch Berechnung des Betrages des Verbindungsvektors von $M$ und $P$ wird die Länge des Stützbalkens berechnet.

Fehlende Rechnungen angeben

Einsetzen des berechneten Parameterwertes $r=\dfrac{12}{5}$ in die Geradengleichung von $g$ liefert die Koordinaten des Schnittpunkts der Dachfläche und des Stützbalkens:

$\begin{array}[t]{rll} \overrightarrow{OP}&=& \pmatrix{3\\0\\12} + \dfrac{12}{5}\cdot \pmatrix{0\\2\\1} & \\[5pt] &=& \pmatrix{3\\ \dfrac{24}{5}\\ \dfrac{72}{5}} \end{array}$

Der Stützbalken und die Dachfläche $GHS$ treffen folglich im Punkt mit den Koordinaten $P\left(3\mid \dfrac{24}{5}\mid \dfrac{72}{5}\right)$ aufeinander.

Die Berechnung der Länge des Stützbalkens über den Betrag des Verbindungsvektors $\overrightarrow{MP}$ ergibt sich wie folgt:

$\begin{array}[t]{rll} \left|\overrightarrow{MP}\right| &=& \left| \pmatrix{0 \\ \frac{24}{5} \\ \frac{12}{5}}\right| \\[5pt] &=& \sqrt{0^2 +\left(\dfrac{24}{5}\right)^2 +\left(\dfrac{12}{5}\right)^2} \\[5pt] &=& \dfrac{12}{\sqrt{5}}\\[5pt] &\approx& 5,37 \;[\text{m}]\\[5pt] \end{array}$

2.2

Mit Punkt $H$ als Stützpunkt folgt für die Geradengleichung von $k:$

$k:\; \overrightarrow{x}$ $= \pmatrix{0\\6\\12} + a\cdot \pmatrix{1\\-1\\1}$

Gleichsetzen mit der Geradengleichung von $g$ liefert:

$a\cdot \pmatrix{1\\-1\\1}-r\cdot \pmatrix{0\\2\\1}= \pmatrix{3\\-6\\0}$

Rechenweg anzeigen

Daraus ergibt sich folgendes lineares Gleichungssystem:

$\begin{array}{} \text{I:}\quad& a &=& 3 \\ \text{II:}\quad& -a-2r &=& -6 \\ \text{III:}\quad& a-r &=& 0 \\ \end{array}$

Aus der ersten Gleichung folgt $a = 3.$

Einsetzen in die zweite Gleichung liefert für $r:$

$\begin{array}[t]{rll} \text{II:}\quad -a-2r &=& -6 & \\[5pt] -3-2r&=& -6 &\quad \scriptsize \mid\; +3\\[5pt] -2r&=& -3 &\quad \scriptsize \mid\;:(-2) \\[5pt] r &=& \dfrac{3}{2} \end{array}$

Einsetzen in die dritte Gleichung zur Überprüfung der Ergebnisse:

$\begin{array}[t]{rll} \text{III:}\quad a-r&=& 0\\[5pt] 3-\dfrac{3}{2}&=& 0 \\[5pt] \dfrac{3}{2} &=& 0 \end{array}$

Das Prüfen der Ergebnisse fürt zu einem Widerspruch, somit ist das Gleichungssystem nicht lösbar. Die Geraden $g$ und $k,$ und damit auch die beiden Stützbalken, schneiden sich folglich nicht.

Lage des Schattenpunktes begründen

Da der Baum $10\;\text{m}$ hoch ist und die Koordinaten des unteren Endes des Baumes durch $Q(24\mid 4\mid 0)$ gegeben sind, folgt für die Koordinaten der Baumspitze $R(24\mid 4\mid 10).$

Da die $x$ -Koordinate größer als $6,$ die $y$ -Koordinate kleiner als $6$ und die $z$ -Koordinate kleiner als $12$ ist, steht der Baum vor der Kirche und ist kleiner als diese.

Da die Einträge des Vektors der die Sonnenstrahlen beschreibt alle negativ sind, kann der Schattenpunkt nur auf der Vorderseite des Turmes mit den Eckpunten $B, C, G$ und $F$ liegen.

Koordinaten des Schattenpunktes bestimmen

Alle Eckpunkte der Vorderseite des Kirchturmes haben die $x$ -Koordinate $6,$ somit liegt diese in der Ebene mit der Gleichung $x = 6.$

Mit Hilfe des Vektors der Sonnenstrahlen als Richtungsvektor und der Baumspitze $R$ als Stützpunkt folgt für die Gerade entlang derer das Licht einfällt:

$g_{\text{Sonne}}: \, \overrightarrow{x} = \pmatrix{24\\4\\10} + s\cdot \pmatrix{-9\\-1\\-1}$

Einsetzen der allgemeinen Koordinaten $P_s(24 -9s \mid 4-s \mid 10- s)$ der Punkte auf der Geraden in die Ebenengleichung liefert:

$\begin{array}[t]{rll} x&=& 6\\[5pt] 24 -9s&=& 6 &\quad \scriptsize \mid\;-24 \\[5pt] -9s&=& -18 &\quad \scriptsize \mid\;:(-9) \\[5pt] s&=& 2 \end{array}$

Einsetzen von $s=2$ in die Geradengleichung liefert den Schattenpunkt:

$\(\begin{array}[t]{rll} \overrightarrow{OR$

Der Schattenpunkt der Kirmesbaumspitze besitzt somit die Koordinaten $\(R$

1.1

Kirchturm einzeichnen

Beginnend mit $A$ im Ursprung und mit Hilfe der in der Aufgabenstellung gegebenen Längenangaben folgt für den Kirchturm:

Koordinaten der Eckpunkte angeben

$C(6\mid6\mid 0)$

$F(6\mid 0\mid 12)$

1.2

Da das Dach eine regelmäßige vierseitige Pyramide ist, sind alle vier Seitenflächen gleichgroß und die Dachfläche ist das Vierfache des Flächeninhalts einer dieser Seitenflächen.

Für die Berechnung von zum Beispiel der Seitenfläche $EFS$ werden die Verbindungsvektoren $\overrightarrow{FE}$ und $\overrightarrow{FS}$ benötigt:

$\begin{array}[t]{rll} \overrightarrow{FE} &=& \pmatrix{0\\0\\12} - \pmatrix{6\\0\\12}& \\[5pt] &=& \pmatrix{-6\\0\\0} \end{array}$

$\begin{array}[t]{rll} \overrightarrow{FS}&=& \pmatrix{3\\3\\18} - \pmatrix{6\\0\\12}& \\[5pt] &=& \pmatrix{-3\\3\\6} \end{array}$

Für den Flächeninhalt folgt mit dem crossP-Befehl des CAS:

Mathematik-Software mit Berechnungen und Formeln zu Vektoren und Normen.

Die gesamte Dachfläche ergibt sich damit zu:

$\begin{array}[t]{rll} A_{\text{Dach}}&=& 4\cdot A_{EFS} & \\[5pt] &=& 4\cdot 9\cdot \sqrt{5}& \\[5pt] &\approx& 80,5 \;[\text{m}^2]& \\[5pt] \end{array}$

2.1.1

Parameterform angeben

$E_{GHS}:\; \overrightarrow{x} = \overrightarrow{OG} + s\cdot \overrightarrow{GS} + t\cdot \overrightarrow{GH}$

Vollständige Gleichung anzeigen

Koordinatengleichung bestimmen

Das Kreuzprodukt aus zwei Spannvektoren der Ebene liefert einen Normalenvektor:

Einsetzen des gekürzten Normalenvektors $\overrightarrow{n} = \pmatrix{0\\2\\1}$ sowie der Koordinaten von $G$ liefert nun:

$\begin{array}[t]{rll} d&=& n_1\cdot x +n_2\cdot y+n_3\cdot z \\[5pt] &=& 0\cdot 6 + 2\cdot 6 + 1\cdot 12 \\[5pt] &=& 24 \end{array}$

Eine Gleichung der Ebene $E_{GHS}$ in Koordinatenform lautet somit:

$E_{GHS}:\; 2\cdot y + z = 24$

Alternativer Lösungsweg:

Aus der zweiten Zeile der Parametergleichung von $E_{GHS}$ folgt:

$\begin{array}[t]{rll} y&=& 6-3\cdot t&\quad \scriptsize \mid\; -6 \\[5pt] y-6&=& -3\cdot t&\quad \scriptsize \mid\; :(-3) \\[5pt] \dfrac{1}{3}\cdot (6-y)&=& t \end{array}$

Damit ergibt sich nun:

$2y+z=24$

Rechenweg anzeigen

Eine Gleichung der Ebene $E_{GHS}$ in Koordinatenform lautet somit:

$E_{GHS}:\; 2\cdot y + z = 24$

2.1.2

Zeilen erläutern

$\text{(1)}$

$\text{(2)}$

$\text{(3)}$

Einsetzen des Wertes von $r$ aus Zeile $\text{(2)}$ in die Geradengleichung ergibt die Koordinaten des Punkts $P,$ in dem der Stützbalken auf die Dachfläche $GHS$ trifft.

$\text{(4)}$

Durch Berechnung des Betrages des Verbindungsvektors von $M$ und $P$ wird die Länge des Stützbalkens berechnet.

Fehlende Rechnungen angeben

Einsetzen des berechneten Parameterwertes $r=\dfrac{12}{5}$ in die Geradengleichung von $g$ liefert die Koordinaten des Schnittpunkts der Dachfläche und des Stützbalkens:

$\begin{array}[t]{rll} \overrightarrow{OP}&=& \pmatrix{3\\0\\12} + \dfrac{12}{5}\cdot \pmatrix{0\\2\\1} & \\[5pt] &=& \pmatrix{3\\ \dfrac{24}{5}\\ \dfrac{72}{5}} \end{array}$

Der Stützbalken und die Dachfläche $GHS$ treffen folglich im Punkt mit den Koordinaten $P\left(3\mid \dfrac{24}{5}\mid \dfrac{72}{5}\right)$ aufeinander.

Die Berechnung der Länge des Stützbalkens über den Betrag des Verbindungsvektors $\overrightarrow{MP}$ ergibt sich wie folgt:

2.2

Mit Punkt $H$ als Stützpunkt folgt für die Geradengleichung von $k:$

$k:\; \overrightarrow{x}$ $= \pmatrix{0\\6\\12} + a\cdot \pmatrix{1\\-1\\1}$

Gleichsetzen mit der Geradengleichung von $g$ liefert:

$a\cdot \pmatrix{1\\-1\\1}-r\cdot \pmatrix{0\\2\\1} = \pmatrix{3\\-6\\0}$

Rechenweg anzeigen

Daraus ergibt sich folgendes lineares Gleichungssystem:

$\begin{array}{} \text{I:}\quad& a &=& 3 \\ \text{II:}\quad& -a-2r &=& -6 \\ \text{III:}\quad& a-r &=& 0 \\ \end{array}$

Aus der ersten Gleichung folgt $a = 3.$

Einsetzen in die zweite Gleichung liefert für $r:$

$\begin{array}[t]{rll} \text{II:}\quad -a-2r &=& -6 & \\[5pt] -3-2r&=& -6 &\quad \scriptsize \mid\; +3\\[5pt] -2r&=& -3 &\quad \scriptsize \mid\;:(-2) \\[5pt] r &=& \dfrac{3}{2} \end{array}$

Einsetzen in die dritte Gleichung zur Überprüfung der Ergebnisse:

$\begin{array}[t]{rll} \text{III:}\quad a-r&=& 0\\[5pt] 3-\dfrac{3}{2}&=& 0 \\[5pt] \dfrac{3}{2} &=& 0 \end{array}$

Das Prüfen der Ergebnisse fürt zu einem Widerspruch, somit ist das Gleichungssystem nicht lösbar. Die Geraden $g$ und $k,$ und damit auch die beiden Stützbalken, schneiden sich folglich nicht.

Lage des Schattenpunktes begründen

Da der Baum $10\;\text{m}$ hoch ist und die Koordinaten des unteren Endes des Baumes durch $Q(24\mid 4\mid 0)$ gegeben sind, folgt für die Koordinaten der Baumspitze $R(24\mid 4\mid 10).$

Da die $x$ -Koordinate größer als $6,$ die $y$ -Koordinate kleiner als $6$ und die $z$ -Koordinate kleiner als $12$ ist, steht der Baum vor der Kirche und ist kleiner als diese.

Da die Einträge des Vektors der die Sonnenstrahlen beschreibt alle negativ sind, kann der Schattenpunkt nur auf der Vorderseite des Turmes mit den Eckpunten $B, C, G$ und $F$ liegen.

Koordinaten des Schattenpunktes bestimmen

Alle Eckpunkte der Vorderseite des Kirchturmes haben die $x$ -Koordinate $6,$ somit liegt diese in der Ebene mit der Gleichung $x = 6.$

Mit Hilfe des Vektors der Sonnenstrahlen als Richtungsvektor und der Baumspitze $R$ als Stützpunkt folgt für die Gerade entlang derer das Licht einfällt:

$g_{\text{Sonne}}: \, \overrightarrow{x} = \pmatrix{24\\4\\10} + s\cdot \pmatrix{-9\\-1\\-1}$

Einsetzen der allgemeinen Koordinaten $P_s(24 -9s \mid 4-s \mid 10- s)$ der Punkte auf der Geraden in die Ebenengleichung liefert:

$\begin{array}[t]{rll} x&=& 6\\[5pt] 24 -9s&=& 6 &\quad \scriptsize \mid\;-24 \\[5pt] -9s&=& -18 &\quad \scriptsize \mid\;:(-9) \\[5pt] s&=& 2 \end{array}$

Einsetzen von $s=2$ in die Geradengleichung liefert den Schattenpunkt:

$\(\begin{array}[t]{rll} \overrightarrow{OR$

Der Schattenpunkt der Kirmesbaumspitze besitzt somit die Koordinaten $\(R$