A2 - Analysis

Regenwasser, das auf das Dach eines Hauses fällt, wird über Dachrinnen und Fallrohre in eine Zisterne geleitet und dort gesammelt.

In einem Beobachtungszeitraum von 15 Uhr bis 16 Uhr wird in der Zisterne die Zuflussgeschwindigkeit gemessen. Zu Beginn des Beobachtungszeitraumes befinden sich bereits 2000 Liter Wasser in der Zisterne.

Der zeitliche Verlauf der Zuflussgeschwindigkeit wird durch die Funktion $z$ mit $z(t)= \left(\dfrac{3}{10}\cdot t^2-t+4 \right)\cdot \mathrm e^{-0,1\cdot t}$ für $0\leq t\leq 60$ beschrieben. Dabei beschreibt $t$ die Zeit ab 15 Uhr in Minuten, $z(t)$ die Zuflussgeschwindigkeit in Liter pro Minute.

1.1

Zeichne den Graphen von $z$ in das Koordinatensystem in Abbildung 1.

Bestimme die maximale und die minimale Zuflussgeschwindigkeit im angegebenen Beobachtungszeitraum sowie die jeweils zugehörigen Uhrzeiten.

Zuflussrate Abflussrate Zisterne Hessen Mathe Abi 2017

Abbildung 1

(7 BE)

1.2

Bestimme, wie viel Liter Regenwasser von 15 Uhr bis 16 Uhr in die Zisterne zugeflossen sind.

(3 BE)

Aus der Zisterne wird im gleichen Beobachtungszeitraum von 15 Uhr bis 16 Uhr mit einer konstanten Abflussgeschwindigkeit Wasser entnommen.

Der zeitliche Verlauf der Abflussgeschwindigkeit wird durch die Funktion $a$ mit $a(t) = 7$ für $0\leq t \leq 60$ beschrieben. Dabei beschreibt $t$ die Zeit ab 15 Uhr in Minuten, $a(t)$ beschreibt die Abflussgeschwindigkeit in Liter pro Minute.

1.3

Zeichne den Graphen von $a$ ebenfalls in das Koordinatensystem in Abbildung 1.

Bestimme, in welchem Zeitraum mehr Wasser zu- als abfließt.

(4 BE)

1.4

Ermittle, um wie viel Liter sich die Wassermenge in der Zisterne im Beobachtungszeitraum geändert hat.

(3 BE)

1.5

Bestätige rechnerisch, dass die Funktion $D$ mit

$D(t)=...$

Funktion anzeigen

eine Stammfunktion der Differenzfunktion der Funktionen $z$ und $a$ ist.

(4 BE)

1.6

Erläutere, was die Funktion $D$ aus Aufgabe 1.5 und der Wert $D(0)$ im Sachzusammenhang beschreiben.

(3 BE)

Die Zisterne kann als ein Rotationskörper mit der $x$ -Achse als Rotationsachse aufgefasst werden, dessen Form und Maße in Abbildung 2 und Abbildung 3 dargestellt sind. Dazu wurde die Zisterne im Vergleich zu ihrer tatsächlichen Lage im Erdreich um $90^{\circ}$ nach rechts gekippt.

Die Punkte $A,$ $B,$ $C,$ $D$ und $E$ liegen auf der oberen Randkurve der Querschnittsfläche der Zisterne. Eine Längeneinheit entspricht einem Dezimeter $(1\,\text{dm}).$

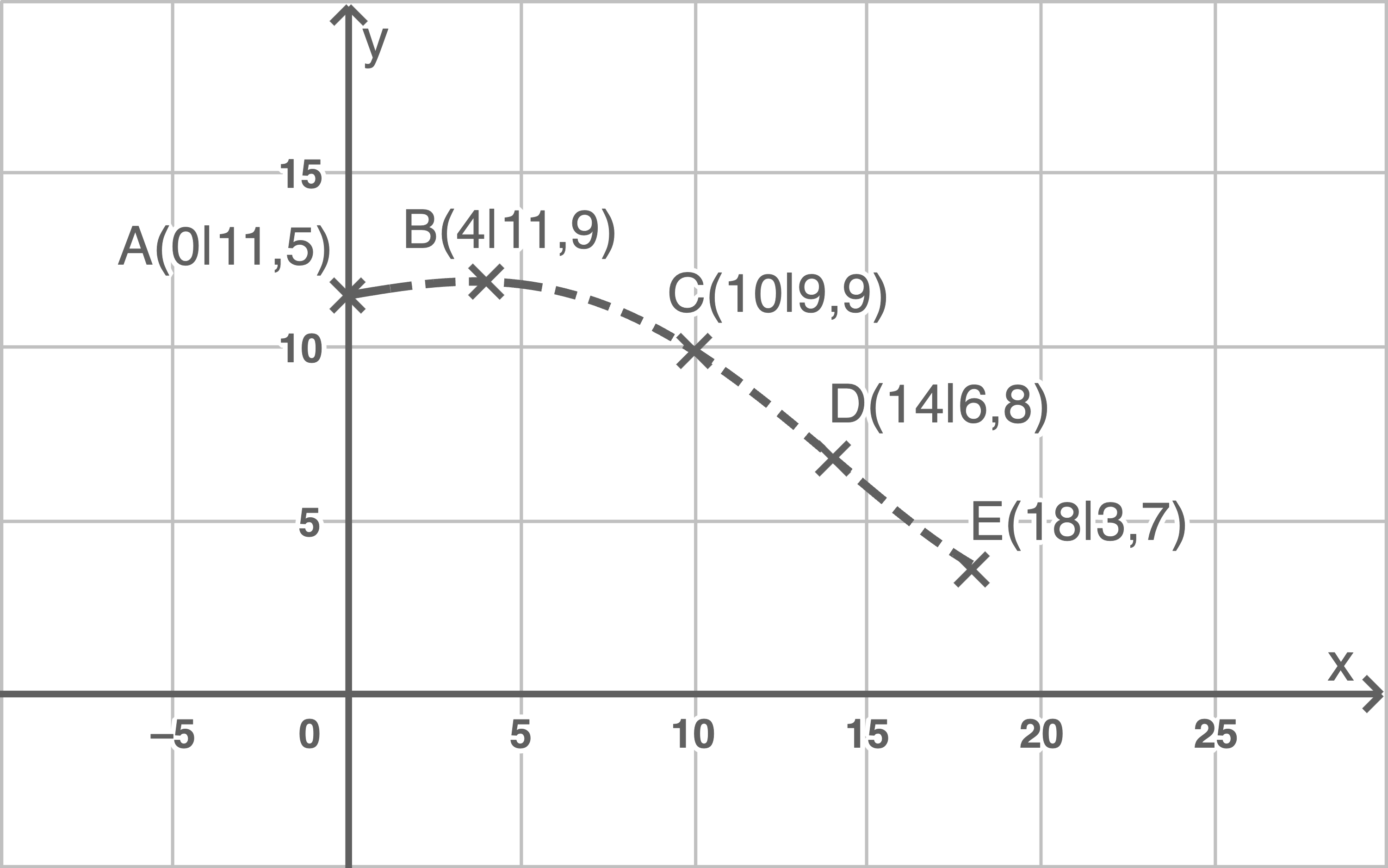
Abbildung 2

Abbildung 3

2.1

Gib eine durch Regression unter Verwendung der Punkte $A,$ $B,$ $C,$ $D$ und $E$ ermittelte ganzrationale Funktion $h$ vierten Grades an, deren Graph die obere Randkurve der Zisterne möglichst gut annähert.

Die Koeffizienten sind auf sechs Nachkommastellen gerundet anzugeben.

(4 BE)

2.2

Für die Funktion $h$ aus Aufgabe 2.1 wird folgende Rechnung durchgeführt:

Rechnung anzeigen

Beschreibe den Aufbau der in der Rechnung enthaltenen fünf Summanden und erläutere die Bedeutung des ermittelten Werts für die Beurteilung der Güte der Approximation.

(5 BE)

2.3

Lässt man den Graphen der Funktion $h$ im Intervall $[0;18]$ um die $x$ -Achse rotieren, erhält man für das Volumen des entstehenden Rotationskörpers das Ergebnis $V_h \approx 5364,5$ Liter.

Das Volumen der Zisterne lässt sich näherungsweise durch Rotation zweier Geraden $g$ und $k$ um die $x$ -Achse bestimmen:

Die Gerade $g$ verläuft für $0 \leq x \leq 10$ parallel zur $x$ -Achse und durch den Punkt $A.$

Die Gerade $k$ verläuft für $10 \leq x \leq 18$ durch die Punkte $C$ und $E.$

Zeichne die Gerade $g$ für $0 \leq x \leq 10$ und die Gerade $k$ für $10 \leq x \leq 18$ in das Koordinatensystem in Abbildung 2 und bestimme die prozentuale Abweichung des Ergebnisses der Volumenberechnung mit Hilfe der Funktionen $g$ und $k$ von dem mit Hilfe der Funktion $h$ erhaltenen Ergebnis $V_h\approx 5364,5$ Liter.

(7 BE)

1.1

Graphen in das Koordinatensystem einzeichnen

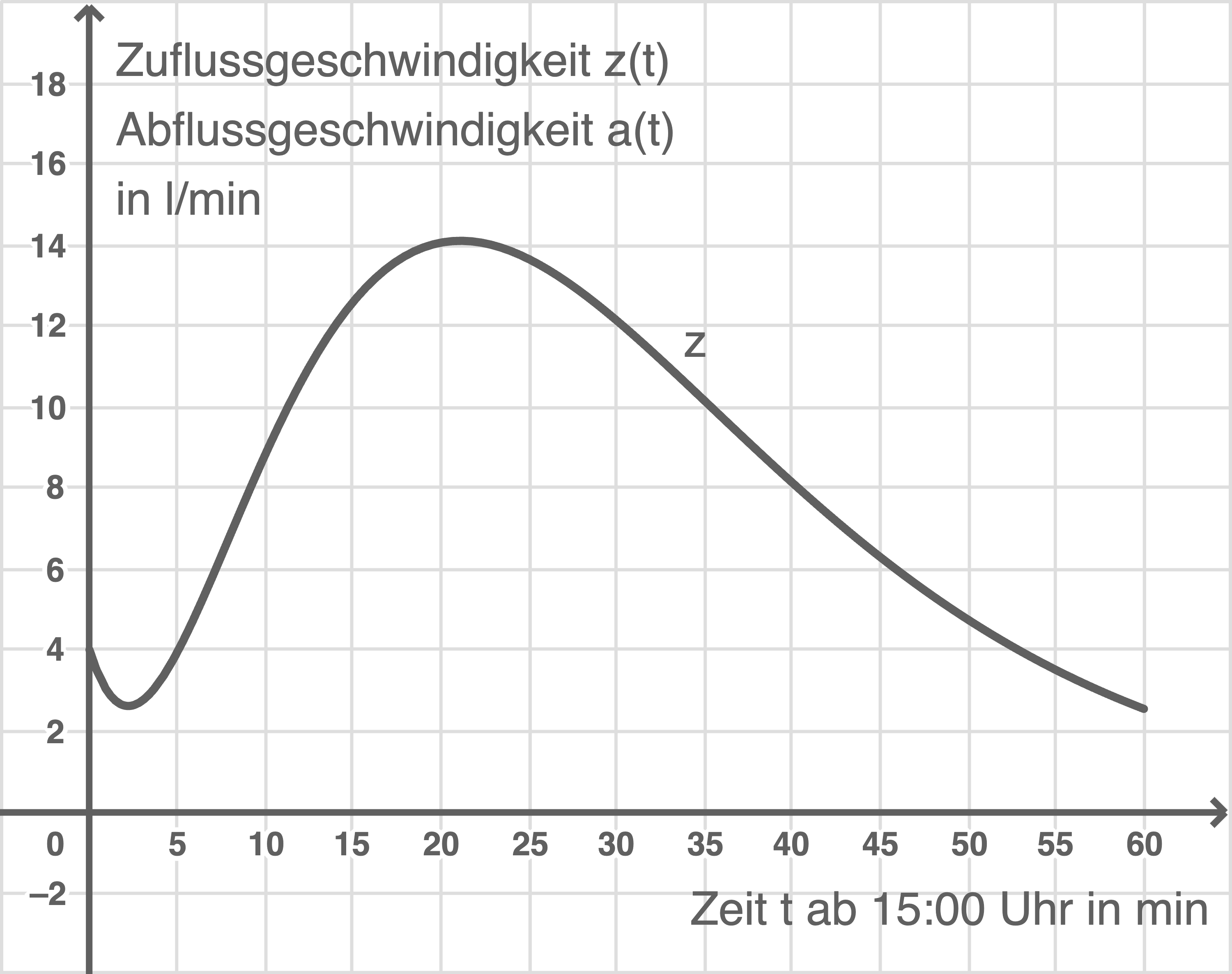
Im Graphik-Menü des CAS lässt sich $z$ graphisch darstellen und die zugehörigen Funktionswerte ablesen.

Einzeichnen in das Koordinatensystem aus der Aufgabenstellung ergibt:

Maximale und minimale Zuflussgeschwindigkeit bestimmen

Die maximale Zuflussgeschwindigkeit entspricht dem maximalen Funktionswert von $z$ im Intervall $[0;60],$ die minimale Zuflussgeschwindigkeit dem minimalen Funktionswert in diesem Intervall.

1. Schritt: Ableitungen bestimmen

Die Funktion $z$ und die beiden Ableitungsfunktionen $\(z$ und $\(z$ werden wie folgt mit Hilfe des CAS definiert:

Keyboard $\to$ Math2

Mathematische Gleichungen und Funktionen in einer Software-Umgebung.

2. Schritt: Notwendige Bedingung für Extremstellen anwenden

Mit dem solve-Befehl des CAS ergibt sich:

$\(\begin{array}[t]{rll} z$

Screenshot einer Software zur Lösung mathematischer Gleichungen und Funktionen.

3. Schritt: Hinreichende Bedingung für Extremstellen anwenden

$\(\begin{array}[t]{rll} z$

Die Funktion $z$ besitzt also ein lokales Minimum an der Stelle $t_1\approx 2,21$ und ein lokales Maximum an der Stelle $t_2 \approx 21,12.$

4. Schritt: Funktionswerte vergleichen

Neben den beiden Extremstellen müssen auch die Randstellen des Intervalls betrachtet werden:

$z(0) = 4$
$z(60)\approx 2,54$
$z(2,21)\approx 2,61$
$z(21,12)\approx 14,12$

Mathematische Berechnungen und Ergebnisse in einem Software-Interface.

Zum Ende des angegebenen Beobachtungszeitraums, also 60 Minuten nach Beobachtungsbeginn um 16 Uhr, ist die Zuflussgeschwindigkeit mit 2,54 Litern pro Minute minimal.

Um ca. 15:21 Uhr ist die Zuflussgeschwindigkeit mit ca. 14,12 Litern pro Minute maximal.

1.2

Die Gesamtmenge des Regenwassers, das im angegebenen Zeitraum in die Zisterne geflossen ist, kann mit Hilfe eines Integrals über $z$ berechnet werden. 15 Uhr entspricht hierbei $t=0$ und 16 Uhr enstpricht $t=60.$

Das Integral $V= \displaystyle\int_{0}^{60}z(t)\;\mathrm dt$ kann mit dem CAS wie folgt berechnet werden:

Keyboard $\to$ Math2

Es ergibt sich:

$\displaystyle\int_{0}^{60}z(t)\;\mathrm dt \approx 504,45$

Mathematische Darstellung eines Integrals mit Ergebnis in einer Softwareanwendung.

Von 15 Uhr bis 16 Uhr sind somit ca. 504,45 Liter Regenwasser in die Zisterne zugeflossen.

1.3

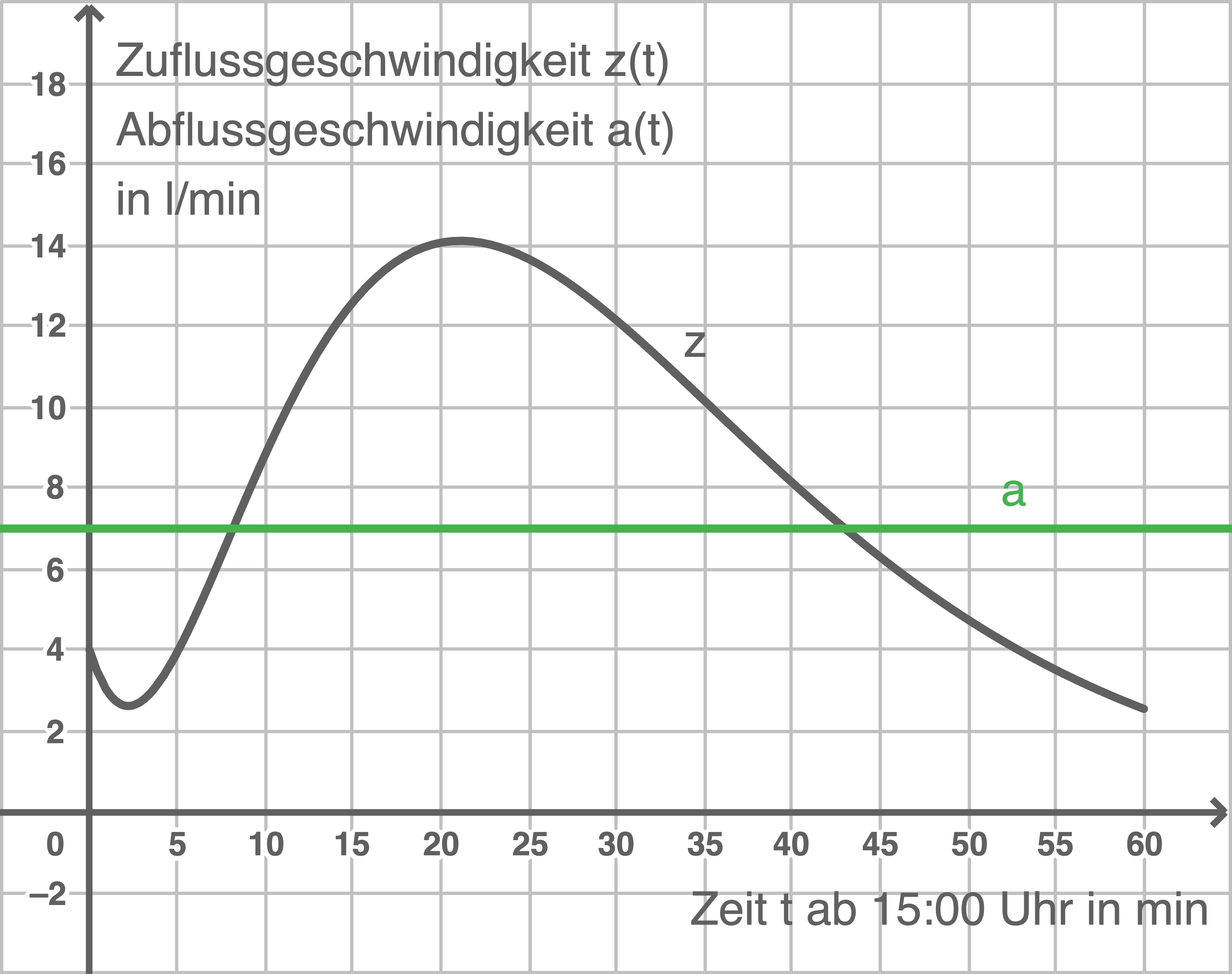
Graphen einzeichnen

Bei dem Graphen von $a$ handelt es sich um eine zur $t$ -Achse parallele Gerade. Es ergibt sich folgende Abbildung:

Zeitraum bestimmen

Es ist der Zeitraum gesucht, in dem die Zuflussgeschwindigkeit des Wassers größer ist als die Abflussgeschwindigkeit, das heißt ein Intervall für $t,$ in dem $z(t) \gt a(t)$ gilt.

Mit dem solve-Befehls des CAS können die Schnittstellen des Graphen von $z$ mit der Geraden $a$ bestimmt werden:

$\begin{array}[t]{rll} z(t)&=& 7 &\quad \scriptsize \mid\; CAS \\[5pt] t_1&\approx & 8,17&\\[5pt] t_2&\approx& 42,99 \end{array}$

Dem Schaubild des Graphen kann entnommen werden, dass zwischen diesen beiden Stellen $z(t) \gt 7$ gilt, somit fließt von ca. 15:08 Uhr bis ca. 15:43 Uhr mehr Wasser zu als ab.

1.4

Aus Aufgabe 1.2 folgt, dass die Menge des Regenwassers, das im gesamten Beobachtungszeitraum in die Zisterne zugeflossen ist, 504,45 Liter beträgt.

Die Abflussgeschwindigkeit, die durch die Funktion $a$ beschrieben wird, beträgt im gesamten Zeitraum konstant 7 Liter pro Minute. Insgesamt ergibt sich also für die abgeflossene Wassermenge:

$V_a = 7\,\dfrac{l}{\text{min}} \cdot 60\,\text{min}$ $= 420\,l$

Die Differenz des Zu- und Abflusses ergibt sich somit zu:

$504,45\, l - 420\,l = 84,46\;l$

Insgesamt hat die Menge des Wassers in der Zisterne im Beobachtungszeitraum also um 84,46 Liter zugenommen.

1.5

$D$ ist genau dann eine Stammfunktion der Differenzenfunktion von $z$ und $a,$ wenn gilt:

$\(D$

Vereinfachen der Funktionsgleichung von $D$ ergibt:

Funktion anzeigen

Mit der Produktregel folgt die erste Ableitung nun mit:

$\( D$

Rechenweg anzeigen

$D$ ist somit eine Stammfunktion der Differenzenfunktion der Funktionen $z$ und $a.$

1.6

Die Differenzenfunktion $d$ gibt Differenz der zu- und abgeflossenen Wassermenge und somit die gesamte momentane Änderungsrate der Wassermenge in der Zisterne an.

Die Funktion $D$ beschreibt somit die Wassermenge in Litern, die sich $t$ Minuten nach 15 Uhr in der Zisterne befindet.

$D(0)=2000$

Rechenweg anzeigen

Der Wert $D(0)$ gibt die Wassermenge in Litern an, die sich zu Beginn der Beobachtung um 15 Uhr in der Zisterne befindet.

Um 15 Uhr befinden sich folglich 2000 Liter Wasser in der Zisterne.

2.1

Allgemeine ganzrationale Funktion vierten Grades:

$h(x)=ax^4 + b^3 + cx^2 + dx + e$

Die Koordinaten der fünf Punkte für die Regression können aus dem Koordinatensystem in Abbildung 2 abgelesen werden. Gesucht sind die Koeffizienten $a,b,c,d$ und $e.$

Nach Eingeben der Koordinaten der koordinaten der fünf Punkte im Statistik-Menü des CAS folgt die Regression vierten Grades mit:

Calc $\to$ Regressionen $\to$ Quart. Regression

Der CAS liefert folgende Koeffizienten:

$a\approx 0,000179$
$b=-0,00506$
$c\approx -0,000357$
$d\approx 0,170952$
$e= 11,5$

Statistische Berechnung einer quartischen Regression mit Werten für a, b, c, d, e und weiteren Parametern.

Eine ganzrationale Funktion vierten Grades, deren Graph die obere Randkurve der Zisterne möglichst gut annähert, ist somit:

$h(x)=...$

Funktion anzeigen

2.2

In den einzelnen Summanden wird die Differenz der Funktionswerte der Näherung $h$ zum vorgegebenen Funktionswert, den die Funktion an dieser Stelle im Idealfall annehmen sollte, berechnet. Diese Abweichung wird anschließend quadriert.

Die Summanden sind also jeweils die quadrierte Abweichung der Näherung zu den eigentlich gegebenen Funktionswerten aus Abbildung 2, die für die Näherung verwendet wurde.

Die Summe dieser quadratischen Abweichungen ist insgesamt $4,57\cdot 10^{-24}.$ Je näher der Wert bei Null liegt, desto besser ist die Approximation. Da $4,57\cdot 10^{-24}$ sehr klein ist, ist die Approximation durch die Funktion $h$ also relativ genau.

2.3

Geraden einzeichnen

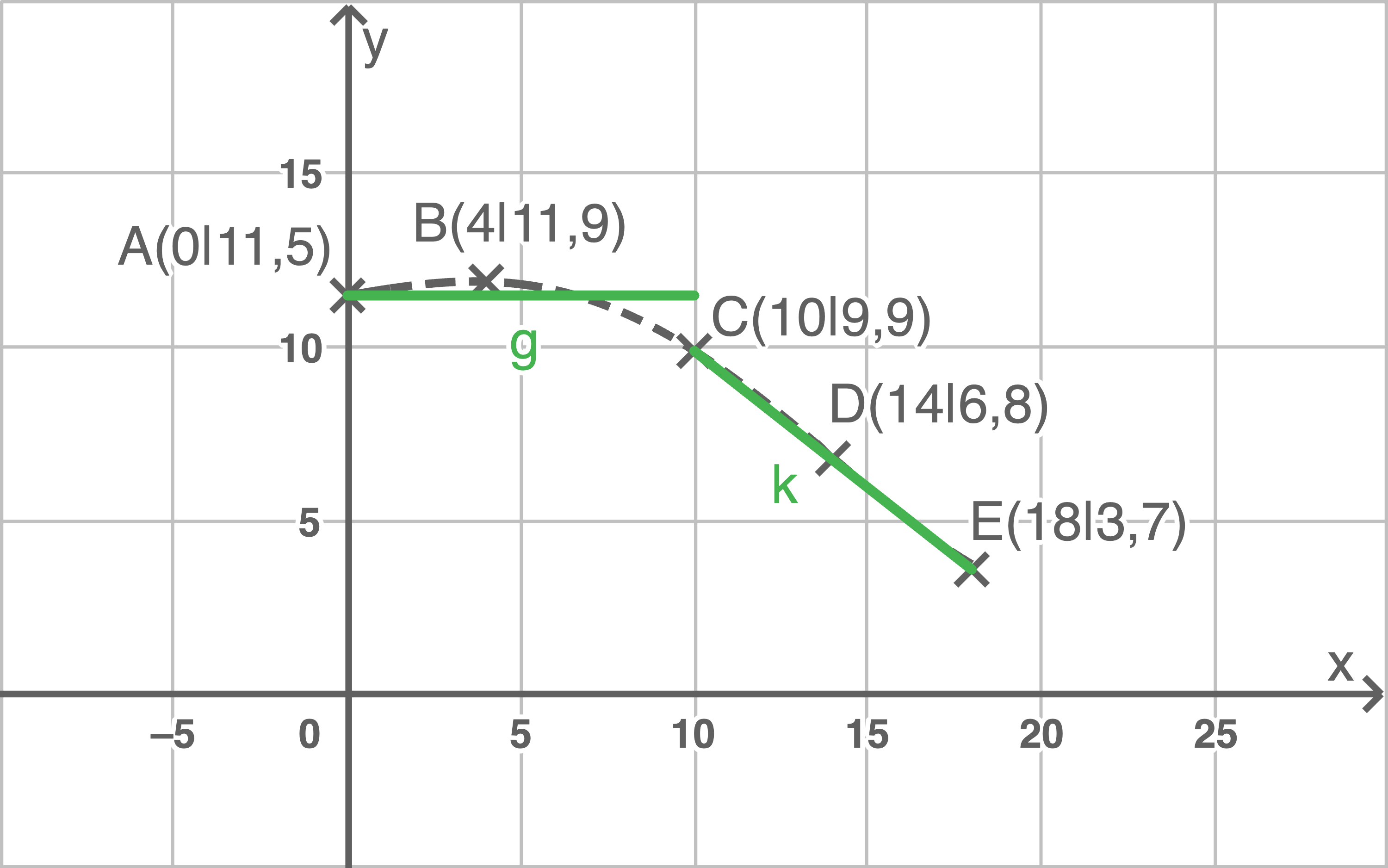Rotationskoerper Randlinie Zistern Hessen Mathe Abi

Prozentuale Abweichung bestimmen

Bei der Rotation der Geraden $g$ um die $x$ -Achse für $0 \leq x \leq 10$ entsteht ein Kreiszylinder mit Radius $r=11,5 \;\text{dm}$ und Höhe $h=10 \;\text{dm}.$ Für das Volumen folgt:

$\begin{array}[t]{rll} V_g&=& \pi\cdot r^2 \cdot h& \\[5pt] &=& \pi\cdot 11,5^2 \cdot 10 \\[5pt] &\approx& 4154,7 \; [\text{dm}^3] \end{array}$

Bei der Rotation von $k$ um die $x$ -Achse entsteht ein Kreiskegelstumpf. Mit Hilfe des Radius der Deckfläche $r_1=3,7 \;\text{dm},$ des Radius der Deckfläche $r_2=9,9 \;\text{dm}$ und der Höhe $h_k= 8 \;\text{dm}$ folgt für das Volumen:

$V_k\approx 1242,6 \; [\text{dm}^3]$

Rechenweg anzeigen

Es gilt: $1 \;\text{dm}^3= 1\,l.$

Die prozentuale Abweichung folgt also mit:

Rechnung anzeigen

Das durch die Geraden $g$ und $k$ ermittelte Volumen ist somit ca. $0,61\,\%$ größer, als das durch die Funktion $h$ ermittelte Volumen.