B1 - Analysis
An einem geradlinigen Küstenabschnitt Niedersachsens soll ein Deich älteren Baujahrs an die zukünftigen Anforderungen des Küstenschutzes angepasst werden.
Bei allen Modellierungen wird die Profillinie des Querschnitts des Deichs und - falls vorhanden - eines Grabens betrachtet. Dabei ist bei der Betrachtung des Querschnitts links des Deichs die Seeseite und rechts des Deichs die Landseite. Der Graben schließt sich auf der Seeseite an den Deich an. Das horizontale ebene Gelände links des Grabens und rechts des Deichs liegt in der Modellierung auf Höhe der  -Achse.
Die Funktionswerte der folgenden Funktionen geben die Höhen bzw. Tiefen des Deichs bzw. des Grabens in Bezug auf dieses ebene Gelände an.
Eine Einheit im Koordinatensystem entspricht einem Meter.
-Achse.
Die Funktionswerte der folgenden Funktionen geben die Höhen bzw. Tiefen des Deichs bzw. des Grabens in Bezug auf dieses ebene Gelände an.
Eine Einheit im Koordinatensystem entspricht einem Meter.
Das Volumen des Erdreichs, welches nach dem Ausgraben eines Siels abtransportiert werden muss, kann durch den Term berechnet werden. Erläutere diesen Term im Sachzusammenhang und bestimme das Volumen in Kubikmetern.

1
Für die Planung lässt sich die bestehende Profillinie des alten Deichs mit einem seeseitig vorgesetzten Graben durch den Graphen der Funktion  mit
mit  für
für  modellieren.
modellieren.
1.1
Beschreibe die Bedeutung der vier Faktoren von  für den Graphen der Funktion
für den Graphen der Funktion 
(3 BE)
1.2
Bestimme die Breite und die Höhe des Deichs sowie die Breite und die Tiefe des Grabens.
(6 BE)
1.3
Skizziere die Profillinie des alten Deichs und des Grabens in das Koordinatensystem in Abbildung 1.
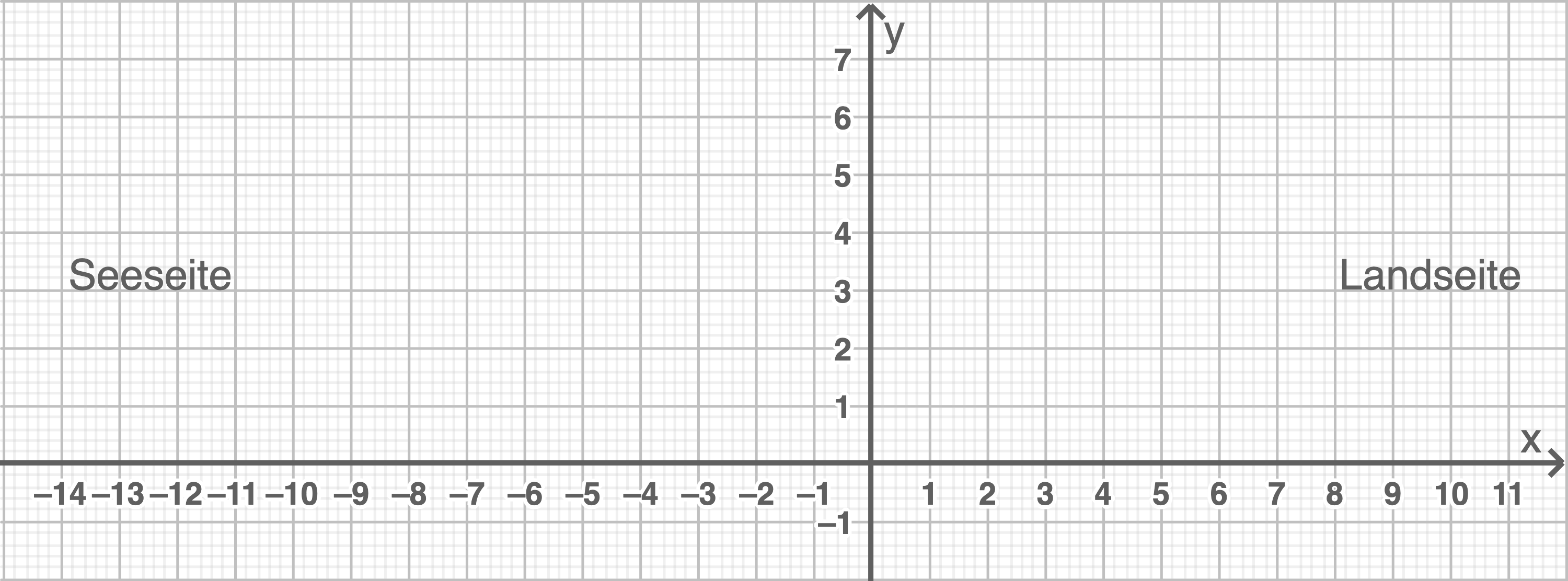

(2 BE)
2
Eine Bürgerinitiative entwickelt eine Alternative zu dem bestehenden Deich. Die Profillinie des alternativen Deichs wird dabei durch den Graphen einer ganzrationalen Funktion  dritten Grades in einem bestimmten Intervall modelliert.
Es sollen folgende Bedingungen gelten:
Die Profillinie beginnt auf der Landseite an der Stelle
dritten Grades in einem bestimmten Intervall modelliert.
Es sollen folgende Bedingungen gelten:
Die Profillinie beginnt auf der Landseite an der Stelle  Der höchste Punkt
Der höchste Punkt  der Profillinie liegt bei
der Profillinie liegt bei  An der Stelle
An der Stelle  besitzt die Profillinie eine Steigung von
besitzt die Profillinie eine Steigung von  Bestimme die Funktionsgleichung der Funktion
Bestimme die Funktionsgleichung der Funktion 
(6 BE)
3
Im Folgenden wird die Profillinie eines neuen Deichs ohne vorgesetzten Graben durch den Graphen der Funktion  mit
mit
 in einem bestimmten Intervall modelliert.
in einem bestimmten Intervall modelliert.
3.1
Skizziere die neue Profillinie, die durch den Graphen der Funktion  modelliert wird, ebenfalls in das Koordinatensystem in Abbildung 1.
Bestimme einen im Sachzusammenhang sinnvollen Definitionsbereich für
modelliert wird, ebenfalls in das Koordinatensystem in Abbildung 1.
Bestimme einen im Sachzusammenhang sinnvollen Definitionsbereich für 
(4 BE)
3.2
Um die Wellenwirkung einer Sturmflut zu minimieren, werden moderne Deichkonstruktionen mit einem sehr flachen Gefälle auf der Seeseite konstruiert.
Berechne den maximalen Steigungswinkel auf der Seeseite des neuen Deichs.
(7 BE)
3.3
Beim Bau des neuen Deichs wird das Erdreich des alten Deichs aus Aufgabe 1 vollständig verwendet und der Graben des alten Deichs wird zugeschüttet.
Ermittle das Volumen des Erdreichs in Kubikmeter, das auf dem  langen Küstenstreifen zusätzlich benötigt wird.
langen Küstenstreifen zusätzlich benötigt wird.
(6 BE)
3.4
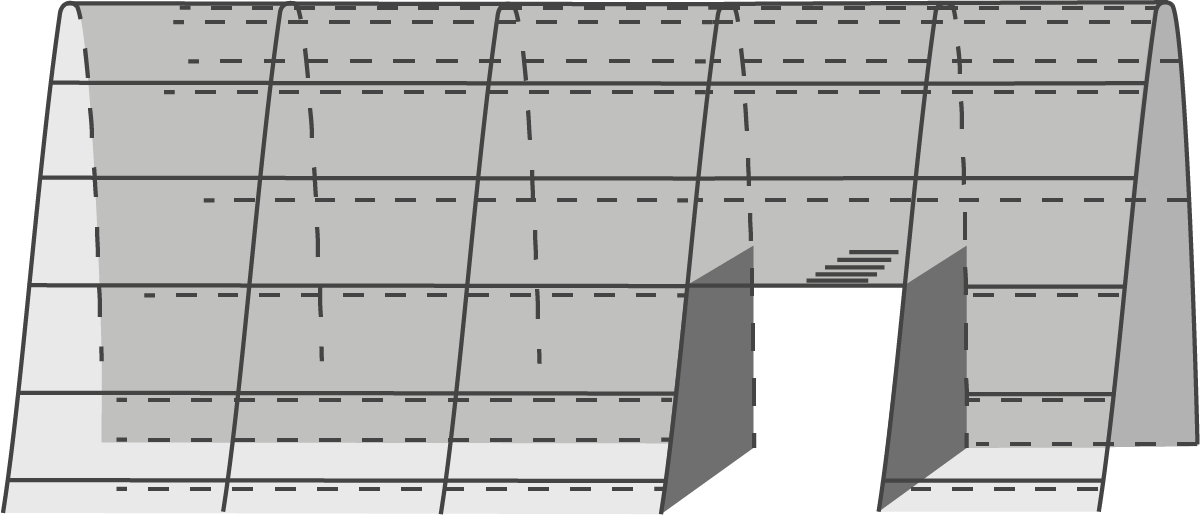
Ein Siel ist ein verschließbarer Gewässerdurchlass in einem Deich.
Der neue Deich wird von einem Siel mit rechteckigem Querschnitt mit einer Breite von  und einer Höhe von
und einer Höhe von  durchtunnelt. Der Boden des Siels befindet sich auf Höhe des horizontalen Geländes.
durchtunnelt. Der Boden des Siels befindet sich auf Höhe des horizontalen Geländes.

Das Volumen des Erdreichs, welches nach dem Ausgraben eines Siels abtransportiert werden muss, kann durch den Term berechnet werden. Erläutere diesen Term im Sachzusammenhang und bestimme das Volumen in Kubikmetern.


(6 BE)
1.1
Der Faktor  staucht den Graphen von
staucht den Graphen von  in
in  -Richtung. Durch das negative Vorzeichen wird die Kurve außerdem an der
-Richtung. Durch das negative Vorzeichen wird die Kurve außerdem an der  -Achse gespiegelt.
Die drei weiteren Faktoren
-Achse gespiegelt.
Die drei weiteren Faktoren  und
und  zeigen die Nullstellen der Funktion
zeigen die Nullstellen der Funktion  an, die entsprechend an den Stellen
an, die entsprechend an den Stellen  und
und  vorliegen.
vorliegen.
1.2
Breite des Deichs bestimmen
Die Breite des Deichs entspricht dem Abstand der zweiten und dritten Nullstelle von 
 Der Deich ist somit
Der Deich ist somit  breit.
Höhe des Deichs bestimmen
Die Höhe des Deichs entspricht dem maximalen Funktionswert von
breit.
Höhe des Deichs bestimmen
Die Höhe des Deichs entspricht dem maximalen Funktionswert von  im Bereich
im Bereich  Dieser lässt sich mit dem CAS berechnen:
Dieser lässt sich mit dem CAS berechnen:
 TI nspire CAS
Mit dem fMax-Befehl kann die Stelle
TI nspire CAS
Mit dem fMax-Befehl kann die Stelle ![\(x\in[0;10],\)](https://www.schullv.de/resources/formulas/db603170bdc9ed96a4e47a7c0937adcf884e1b36d4662047afbcd2d9cc294a01_light.svg) an der der Funktionswert von
an der der Funktionswert von  am größten ist, bestimmt werden.
am größten ist, bestimmt werden.
 Es folgt:
Es folgt:  Der zugehörige Funktionswert lässt sich ebenfalls mit dem CAS berechnen:
Der zugehörige Funktionswert lässt sich ebenfalls mit dem CAS berechnen:
![\(d(7,06) \approx 3,5 \, [\text{m}] \)](https://www.schullv.de/resources/formulas/bf9706289b3bbbd40a3a87d154ad83c838bda3f901e497494cb3557650c2e259_light.svg)
 Casio Classpad II
Mit dem fMax-Befehl kann der größte Funktionswert von
Casio Classpad II
Mit dem fMax-Befehl kann der größte Funktionswert von  im angegebenen Intervall und die zugehörige Stelle
im angegebenen Intervall und die zugehörige Stelle  bestimmt werden.
bestimmt werden.

![\(\begin{array}[t]{rll}
d(x_{\text{max}})&=& 3,5\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/dcd5491cd8418a6e8ab19987c4877e0afda1b436402bc69d18ae6b16f9bcd803_light.svg) Der Deich ist somit
Der Deich ist somit  hoch.
Breite des Grabens bestimmen
Die Breite des Grabens entspricht dem Abstand der ersten und zweiten Nullstelle von
hoch.
Breite des Grabens bestimmen
Die Breite des Grabens entspricht dem Abstand der ersten und zweiten Nullstelle von 
 Der Graben ist somit
Der Graben ist somit  breit.
Tiefe des Grabens bestimmen
Die Tiefe des Grabens entspricht dem minimalen Funktionswert von
breit.
Tiefe des Grabens bestimmen
Die Tiefe des Grabens entspricht dem minimalen Funktionswert von  im Bereich
im Bereich  Dieser lässt sich mit dem CAS analog zur Höhe des Deichs mit dem fMin-Befehl bestimmen:
Dieser lässt sich mit dem CAS analog zur Höhe des Deichs mit dem fMin-Befehl bestimmen:
 Der Graben ist folglich
Der Graben ist folglich  tief.
tief.
1.3
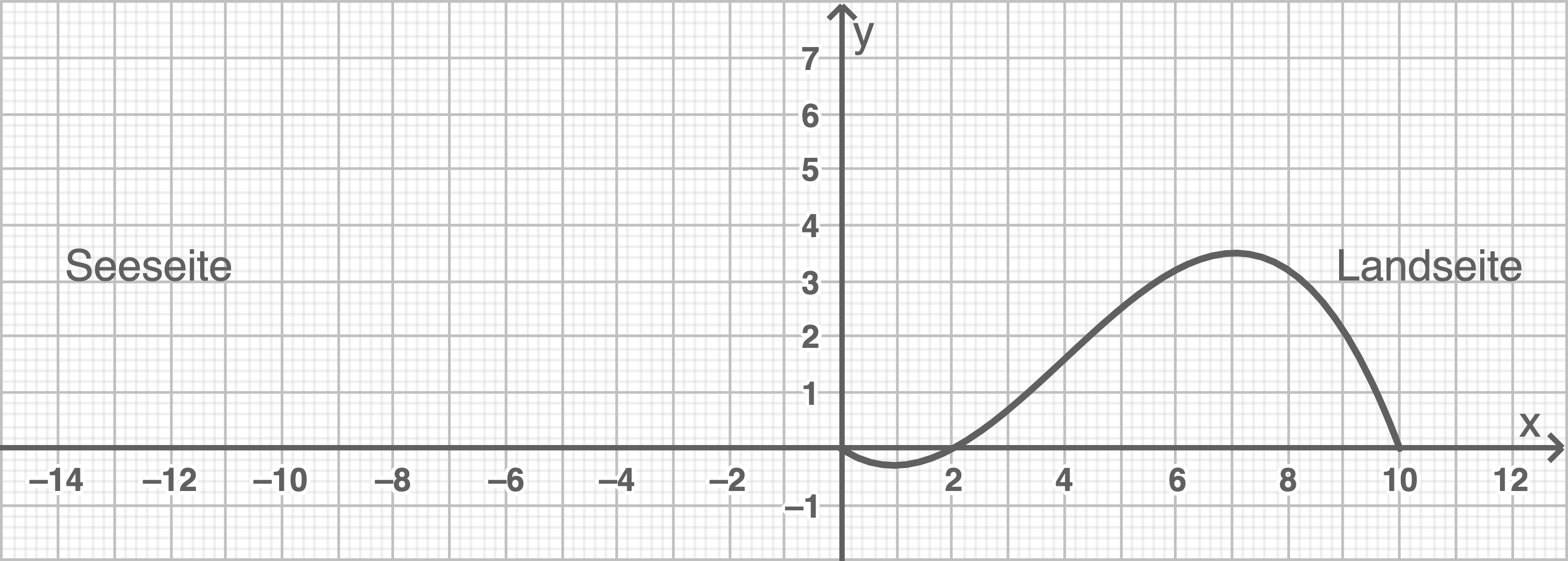
2
Aus dem Aufgabentext folgt für 
![\(\begin{array}[t]{rll}
g(x) &=& a\cdot x^3 +b\cdot x^2 +c\cdot x +d \\[5pt]
g‘(x) &=& 3a\cdot x^2 + 2b\cdot x + c
\end{array}\)](https://www.schullv.de/resources/formulas/ad267bc483306d95dfa71c757a00ce1fffd692053232ddbdc6c532638798b291_light.svg) Im CAS lassen sich nun die Funktionen
Im CAS lassen sich nun die Funktionen  und
und  in Abhängigkeit von
in Abhängigkeit von 

 und
und  definieren.
Anschließend lässt sich das Gleichungssystem aus den vier Bedingungen mit dem solve-Befehl lösen:
definieren.
Anschließend lässt sich das Gleichungssystem aus den vier Bedingungen mit dem solve-Befehl lösen:
 TI nspire CAS
TI nspire CAS
 Casio Classpad II
Es folgt:
Casio Classpad II
Es folgt:
![\(\begin{array}[t]{rll}
g(x)&=& -\dfrac{57}{4060}x^3 -\dfrac{3}{8120}x^2 + \dfrac{687}{1015}x +\dfrac{1824}{1015} & \\[5pt]
&\approx& -0,0140\cdot x^3 - 0,0004\cdot x^2 + 0,6768\cdot x+ 1,7970
\end{array}\)](https://www.schullv.de/resources/formulas/4f2ba3f089f859b2099ccd262371c3620fe4010bd4fce1c62b9f7d5cbcdef28f_light.svg)
menu  3: Algebra
3: Algebra  7
7
keyboard  Math1
Math1 

3.1
Profillinie skizzieren
 Definitionsbereich bestimmen
Ein sinnvoller Definitionsbereich ist genau der Bereich, der die gesamte Breite des Deichs abdeckt und somit der Bereich zwischen den beiden Nullstellen:
Definitionsbereich bestimmen
Ein sinnvoller Definitionsbereich ist genau der Bereich, der die gesamte Breite des Deichs abdeckt und somit der Bereich zwischen den beiden Nullstellen:
![\(D_f = [-10; 10]\)](https://www.schullv.de/resources/formulas/ffc8b0300eb3b9530e8954d48eb84ce55c0090e760e1cd5ccf69fda44c133cc7_light.svg)

3.2
Auf der Seeseite ist die Steigung des Graphen von  positiv. Gesucht ist also die maximale Steigung des Graphen von
positiv. Gesucht ist also die maximale Steigung des Graphen von  für
für  Die Steigung wird durch
Die Steigung wird durch  beschrieben.
1. Schritt: Ableitungsfunktionen bilden
beschrieben.
1. Schritt: Ableitungsfunktionen bilden
![\(\begin{array}[t]{rll}
f(x) &=& -\dfrac{1}{400}\cdot x^3 - \dfrac{3}{100}\cdot x^2 +\dfrac{1}{4} \cdot x +3 \\[5pt]
f](https://www.schullv.de/resources/formulas/ea0a114622be9536120bea54c134231838bd364a86b16c9d0ee5fdce9e40afb2_light.svg) 2. Schritt: Notwendige Bedingung für Extremstellen anwenden
2. Schritt: Notwendige Bedingung für Extremstellen anwenden
![\(\begin{array}[t]{rll}
f](https://www.schullv.de/resources/formulas/eabfb2575747b450c5ab565df78107951598599269fa872eab12efd5dd845b75_light.svg) 3. Schritt: Hinreichende Bedingung für Extremstellen anwenden
3. Schritt: Hinreichende Bedingung für Extremstellen anwenden
 An der Stelle
An der Stelle  besitzt der Graph von
besitzt der Graph von  also ein lokales Maximum.
4. Schritt: Steigungswinkel bestimmen
also ein lokales Maximum.
4. Schritt: Steigungswinkel bestimmen
![\(\begin{array}[t]{rll}
f](https://www.schullv.de/resources/formulas/cea1adfb49ae84c4e13c443a7aa15f4bfe9faac79045baf0e181ee1356a61dfb_light.svg) Der zugehörige Winkel folgt mit:
Der zugehörige Winkel folgt mit:
![\(\begin{array}[t]{rll}
\tan \alpha &=& 0,37 &\quad \scriptsize \mid\;\tan^{-1} \\[5pt]
\alpha &\approx& 20,3^{\circ}
\end{array}\)](https://www.schullv.de/resources/formulas/a34a98ee7a2dba078e6d58c158079c2c55bdbea115fcfede66e652e166080cb7_light.svg) Auf der Seeseite des neuen Deichs beträgt der maximale Steigungswinkel folglich ca.
Auf der Seeseite des neuen Deichs beträgt der maximale Steigungswinkel folglich ca. 
3.3
1. Schritt: Verfügbares Volumen bestimmen
Da der Küstenstreifen  lang ist, ergibt sich:
lang ist, ergibt sich:
![\(\begin{array}[t]{rll}
V_v&=& 125\cdot \displaystyle\int_{2}^{10}d(x)\;\mathrm dx \\[5pt]
&=& 125\cdot \displaystyle\int_{2}^{10}-\frac{1}{30}\cdot x \cdot (x-2)\cdot (x-10)\;\mathrm dx &\quad \scriptsize\mid \; CAS \\[5pt]
&=& \dfrac{6400}{3}\,[\text{m}^3]
\end{array}\)](https://www.schullv.de/resources/formulas/f158eb190b51a447aaafa650f32652d951f0a9ce0cb898c0d5cffd750c1f5bf2_light.svg) 2. Schritt: Benötigtes Volumen zum Aufschütten des Grabens bestimmen
2. Schritt: Benötigtes Volumen zum Aufschütten des Grabens bestimmen
![\(\begin{array}[t]{rll}
V_G&=& 125\cdot \left| \displaystyle\int_{0}^{2}d(x)\;\mathrm dx \right| \\[5pt]
&=& 125\cdot \left|\displaystyle\int_{0}^{2}-\frac{1}{30}\cdot x \cdot (x-2)\cdot (x-10)\;\mathrm dx \right| &\quad \scriptsize\mid \; CAS \\[5pt]
&=& 50\,[\text{m}^3]
\end{array}\)](https://www.schullv.de/resources/formulas/cfbd43e5bc3f5d50d4c484ef00fe6cfd3bf8861862b103f602a0986afe5b7132_light.svg) 3. Schritt: Volumen des neuen Deichs bestimmen
3. Schritt: Volumen des neuen Deichs bestimmen
![\(\begin{array}[t]{rll}
V_n&=& 125\cdot \displaystyle\int_{-10}^{10}f(x)\;\mathrm dx \\[5pt]
&=& 125\cdot \displaystyle\int_{-10}^{10}\left(-\frac{1}{400}\cdot x^3 - \frac{3}{100}\cdot x^2 +\frac{1}{4} \cdot x +3\right)\;\mathrm dx &\quad \scriptsize\mid \; CAS \\[5pt]
&=& 5000 \,[\text{m}^3]
\end{array}\)](https://www.schullv.de/resources/formulas/374d72e93e13032047242a0f4281716373a030bf362a3ce033595548fda45116_light.svg) 4. Schritt: Benötigtes Volumen bestimmen
4. Schritt: Benötigtes Volumen bestimmen
![\(\begin{array}[t]{rll}
V_b &=& V_n + V_G - V_v \\[5pt]
&=& 5000 \,\text{m}^3 + 50\,\text{m}^3 - \frac{6400}{3}\,\text{m}^3\\[5pt]
&=& \frac{8750}{3}\,\text{m}^3 \\[5pt]
&\approx& 2917\,\text{m}^3 \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/f92c753717f1148794196653a9d3e5277ab8e7a7f41d609c43da72d9400684ba_light.svg) Es werden somit zusätzlich ca.
Es werden somit zusätzlich ca.  Erde benötigt.
Erde benötigt.
3.4
Term erläutern
Der Graph von  beschreibt den Verlauf des Deiches im Querschnitt und die obere Begrenzung des Siels wird durch die Gerade
beschreibt den Verlauf des Deiches im Querschnitt und die obere Begrenzung des Siels wird durch die Gerade  beschrieben.
beschrieben.
 und
und  sind die Schnittstellen von
sind die Schnittstellen von  und der Geraden
und der Geraden  Die Querschnittsfläche des Siels lässt sich damit in drei Teilfächen aufteilen:
Die Querschnittsfläche des Siels lässt sich damit in drei Teilfächen aufteilen:
 Der Flächeninhalt der Querschnittsfläche wird anschließend mit der Breite des Siels von
Der Flächeninhalt der Querschnittsfläche wird anschließend mit der Breite des Siels von  multipliziert.
multipliziert.
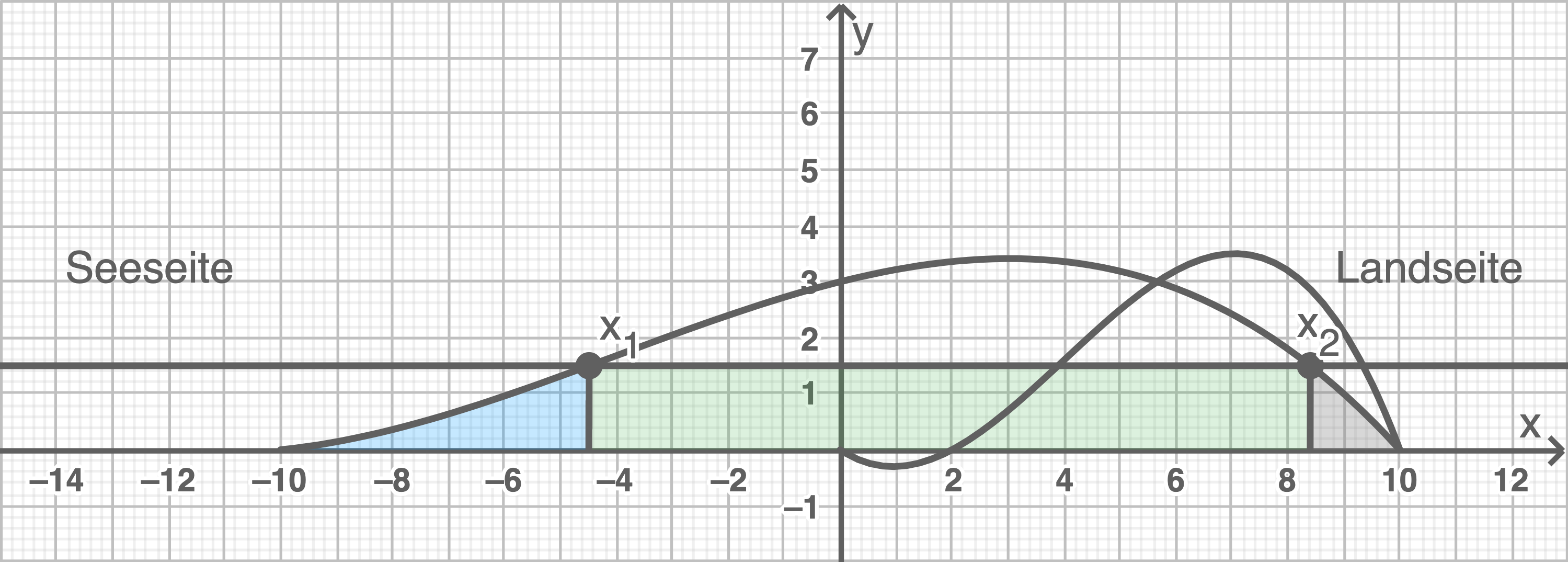 Volumen bestimmen
Mit dem solve-Befehl des CAS ergeben sich die Grenzen
Volumen bestimmen
Mit dem solve-Befehl des CAS ergeben sich die Grenzen  und
und 
![\(\begin{array}[t]{rll}
f(x) &=& 1,5 \\[5pt]
x_1 &\approx& -4,49 \\[5pt]
x_2 &\approx& 8,40
\end{array}\)](https://www.schullv.de/resources/formulas/54495611890cdec2ce25342c27f04632af7f5c4abf7d2b73c9f1f8be4ae5e4d0_light.svg) Mit dem CAS folgt dann:
Mit dem CAS folgt dann:
![\(\begin{array}[t]{rll}
V &=& 2,5\cdot \left( \displaystyle\int_{-10}^{x_1}f(x)\;\mathrm dx + (x_2-x_1)\cdot 1,5 + \displaystyle\int_{x_2}^{10}f(x)\;\mathrm dx\right) &\quad \scriptsize \mid\; CAS \\[5pt]
&\approx& 60,14 \,[\text{m}^3]
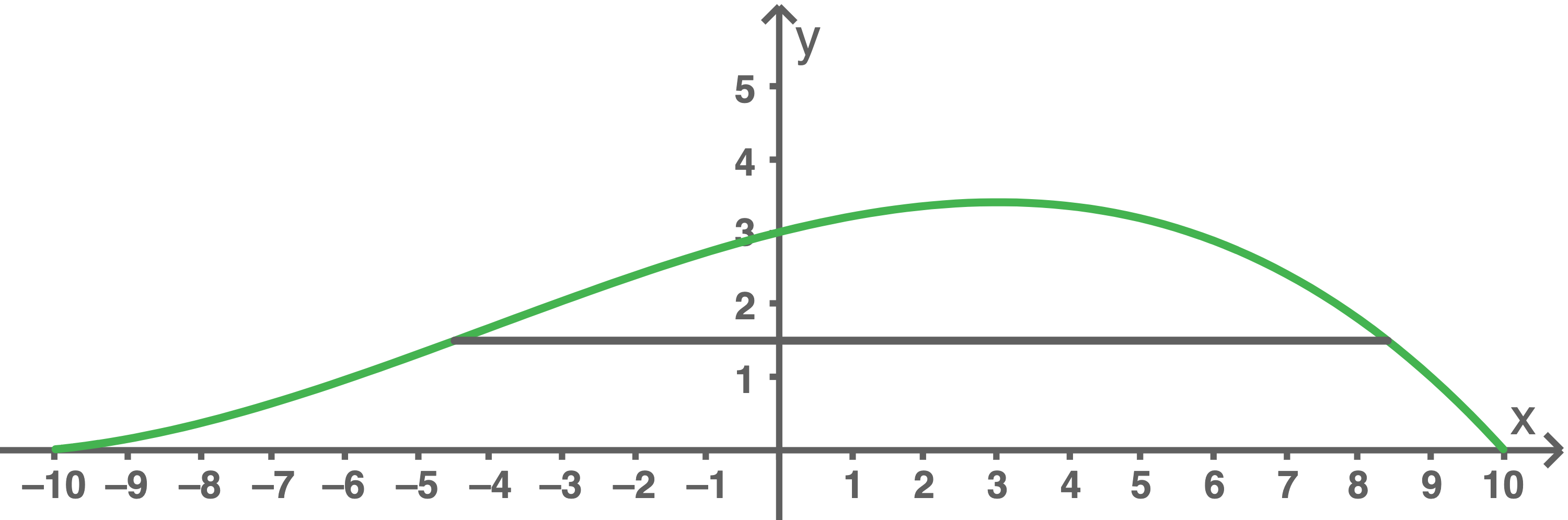
\end{array}\)](https://www.schullv.de/resources/formulas/6d52f9ae81ce8381d9d625b638f3bfa67d1f891c9d0331f919441fa3b14e9396_light.svg) Das Volumen des abzutransportierenden Erdreichs beträgt somit ca.
Das Volumen des abzutransportierenden Erdreichs beträgt somit ca. 
- Die in der Skizze blaue Fläche, deren Flächeninhalt mit Hilfe des Integrals
berechnet werden kann.
- Das in der Skizze grüne Rechteck, dessen Flächeninhalt über
berechnet werden kann.
- Die in der Skizze graue Fläche, deren Flächeninhalt durch
berechnet werden kann.

Hilfsskizze