A1 - Analysis
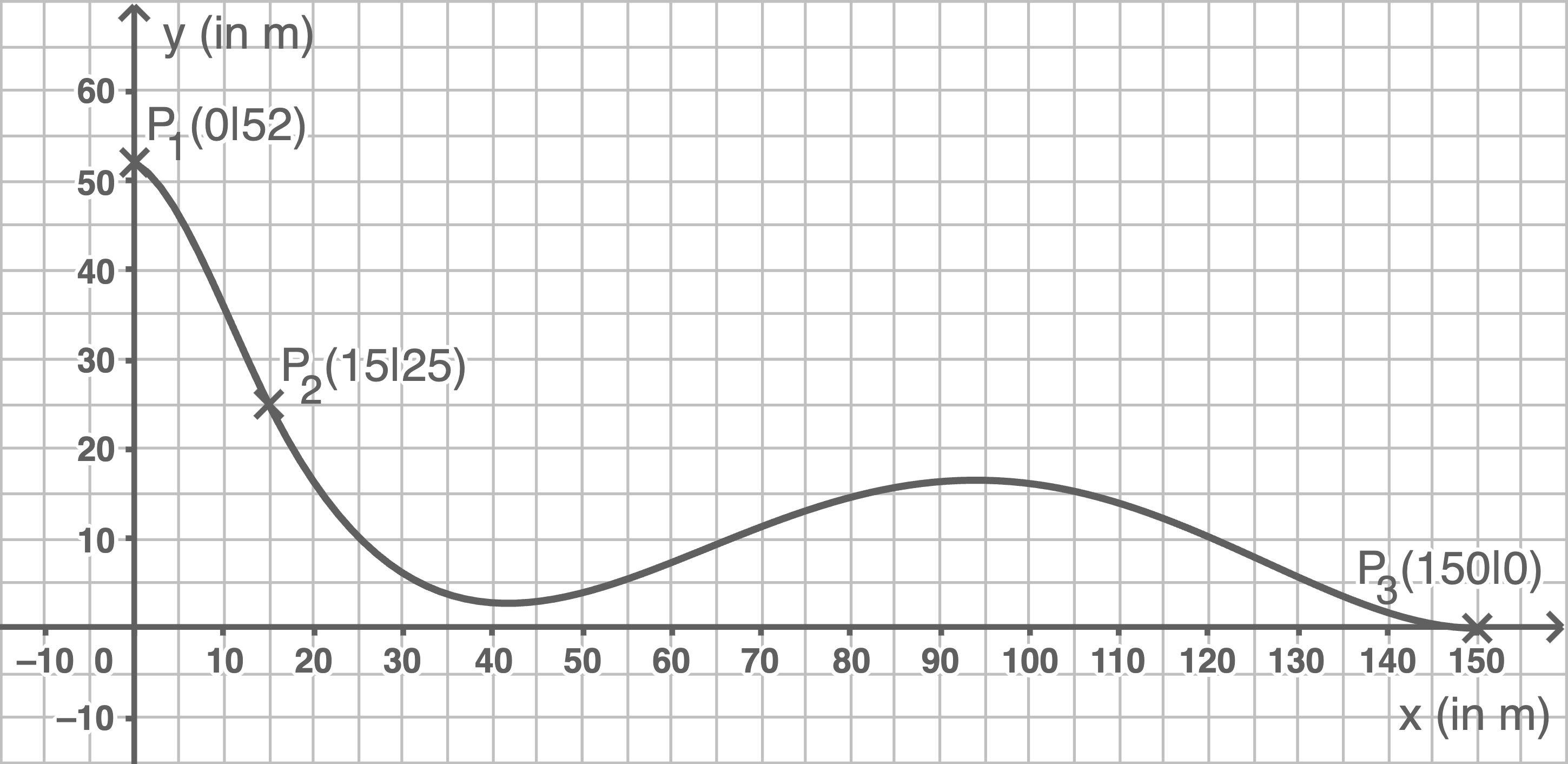
Die mit über 51 Metern - gute 17 Stockwerke - höchste Wasserrutsche der Welt namens „Verrückt“, die mit Schlauchbooten befahren wird, befindet sich im US-Bundesstaat Kansas.
Der Verlauf der Wasserrutsche soll durch die Graphen von zwei ganzrationalen Funktionen modelliert werden. Der Graph der ersten Funktion  beschreibt den Verlauf des ersten Teils der Wasserrutsche vom Startpunkt
beschreibt den Verlauf des ersten Teils der Wasserrutsche vom Startpunkt  bis zum Punkt
bis zum Punkt  und der Graph der zweiten Funktion
und der Graph der zweiten Funktion  den Verlauf des zweiten Teils vom Punkt
den Verlauf des zweiten Teils vom Punkt  bis zum Punkt
bis zum Punkt  Die
Die  -Achse beschreibt den ebenen Erdboden.
Im Folgenden sind alle Längen und Koordinaten in Meter angegeben.
-Achse beschreibt den ebenen Erdboden.
Im Folgenden sind alle Längen und Koordinaten in Meter angegeben.
1
Zunächst soll der Verlauf des zweiten Teils der Wasserrutsche durch eine ganzrationale Funktion modelliert werden.
1.1
Begründe anhand des Graphen, dass die gesuchte ganzrationale Funktion mindestens vierten Grades sein muss.
(2 BE)
1.2
Der Graph der Funktion  verläuft durch die Punkte
verläuft durch die Punkte  und
und  Die Steigung im Übergangspunkt
Die Steigung im Übergangspunkt  beträgt
beträgt  und im Punkt
und im Punkt  geht die Rutsche waagerecht ins Auffangbecken über. Der Steigungswinkel des Graphen an der Stelle
geht die Rutsche waagerecht ins Auffangbecken über. Der Steigungswinkel des Graphen an der Stelle  beträgt
beträgt  Gib einen Ansatz zur Bestimmung einer ganzrationalen Funktion vierten Grades mit den genannten Eigenschaften an und bestimme die Funktionsgleichung.
Gib einen Ansatz zur Bestimmung einer ganzrationalen Funktion vierten Grades mit den genannten Eigenschaften an und bestimme die Funktionsgleichung.
Im Folgenden soll der Verlauf des zweiten Teils der Wasserrutsche durch den Graphen der Funktion
(5 BE)
1.3
Auf einer Werbetafel für den Freizeitpark soll die maximale Höhe des zweiten Teils der Wasserrutsche angegeben werden.
Ermittle ohne Verwendung des Graphen die maximale Höhe innerhalb des Intervalls ![\([80;140].\)](https://www.schullv.de/resources/formulas/1f8219025f02e975ea3eacbd1fdd4273aeb14aca3e68cf94838b1bc13ba15a11_light.svg) Im weiteren Verlauf der Rutsche interessiert das maximale Gefälle. Bestimme das maximale Gefälle innerhalb des Intervalls
Im weiteren Verlauf der Rutsche interessiert das maximale Gefälle. Bestimme das maximale Gefälle innerhalb des Intervalls ![\([80;140].\)](https://www.schullv.de/resources/formulas/1f8219025f02e975ea3eacbd1fdd4273aeb14aca3e68cf94838b1bc13ba15a11_light.svg)
(8 BE)
2
Der Verlauf der Wasserrutsche von  nach
nach  soll aufgrund der hohen Geschwindigkeit, mit der ein Schlauchboot herunterfährt, im Übergangspunkt
soll aufgrund der hohen Geschwindigkeit, mit der ein Schlauchboot herunterfährt, im Übergangspunkt  sowohl knickfrei als auch krümmungsruckfrei sein und dort auch keinen Sprung aufweisen.
sowohl knickfrei als auch krümmungsruckfrei sein und dort auch keinen Sprung aufweisen.
2.1
Um die Bedingung „knickfrei“ einzuhalten, darf die erste Ableitung der Funktion keine Sprungstelle haben.
Erläutere diese Bedingung im Sachzusammenhang und gehe dabei auf mögliche Folgen für den Bewegungsablauf des Schlauchboots an der Übergangsstelle ein.
(3 BE)
2.2
Beschreibe die Eigenschaft „krümmungsruckfrei“ im Übergangspunkt  mathematisch.
mathematisch.
(3 BE)
2.3
Zur Modellierung des Verlaufs des ersten Teils der Wasserrutsche von  nach
nach  werden die Graphen der Funktionen
werden die Graphen der Funktionen  und
und  mit
mit  und
betrachtet.
Beurteile auf rechnerischer Grundlage, welcher der beiden Graphen zur Modellierung des Verlaufs des ersten Teils der Wasserrutsche für den Übergang im Punkt
und
betrachtet.
Beurteile auf rechnerischer Grundlage, welcher der beiden Graphen zur Modellierung des Verlaufs des ersten Teils der Wasserrutsche für den Übergang im Punkt  besser geeignet ist.
besser geeignet ist.
(9 BE)
3
Um die Rutsche für die Besucher bereits von Weitem gut sichtbar zu machen, soll der Bereich unterhalb der gesamten Rutsche zwischen  und
und  mit einer senkrecht zum Boden verlaufenden Werbefläche versehen werden. Diese Werbefläche soll bis auf eine Höhe von
mit einer senkrecht zum Boden verlaufenden Werbefläche versehen werden. Diese Werbefläche soll bis auf eine Höhe von  über dem ebenen Boden herunterreichen.
Bestimme den Flächeninhalt der entstehenden Werbefläche.
über dem ebenen Boden herunterreichen.
Bestimme den Flächeninhalt der entstehenden Werbefläche.
(10 BE)
1.1
Der Graph in Abbildung 2 besitzt zwischen dem Punkt  und dem Punkt
und dem Punkt  drei Stellen, an denen seine Steigung Null ist:
drei Stellen, an denen seine Steigung Null ist:
 und dem Punkt
und dem Punkt  zwei Wendestellen.
Aus der notwendigen Bedingung für Wendestellen folgt, dass die zweite Ableitungsfunktion also zwei Nullstellen besitzt. Die zweite Ableitungsfunktion ist somit mindestens eine ganzrationale Funktion zweiten Grades.
Für die Ausgangsfunktion folgt also, dass sie mindestens eine ganzrationale Funktion vierten Grades sein muss, da mit jedem Ableiten ein Grad verloren geht.
zwei Wendestellen.
Aus der notwendigen Bedingung für Wendestellen folgt, dass die zweite Ableitungsfunktion also zwei Nullstellen besitzt. Die zweite Ableitungsfunktion ist somit mindestens eine ganzrationale Funktion zweiten Grades.
Für die Ausgangsfunktion folgt also, dass sie mindestens eine ganzrationale Funktion vierten Grades sein muss, da mit jedem Ableiten ein Grad verloren geht.
- Einen Tiefpunkt an der Stelle
- Einen Hochpunkt an der Stelle
- Einen weiteren Punkt mit waagerechter Tangente an der Stelle
, der entweder ein Tiefpunkt oder ein Sattelpunkt ist.
1.2
Ansatz angeben
Allgemeine Gleichung einer ganzrationalen Funktion vierten Grades:
 Aus der Aufgabenstellung ergeben sich folgende Bedingungen:
Aus der Aufgabenstellung ergeben sich folgende Bedingungen:



 und
und  Funktionsgleichung bestimmen
Nach dem Definieren der Funktion
Funktionsgleichung bestimmen
Nach dem Definieren der Funktion  und dem Eingeben des GLeichungssystems in den CAS kann das lineare Gleichungssystem unter Keyboard
und dem Eingeben des GLeichungssystems in den CAS kann das lineare Gleichungssystem unter Keyboard  Math1 gelöst werden.
Der CAS liefert folgende Werte:
Math1 gelöst werden.
Der CAS liefert folgende Werte:

- Der Graph verläuft durch den Punkt
es gilt also:
- Der Graph verläuft durch den Punkt
es gilt also:
- Die Steigung des Graphen im Übergangspunkt
beträgt
es muss also gelten:
- Im Punkt
geht die Rutsche waagerecht ins Auffangbecken über:
- An der Stelle
beträgt der Steigungswinkel

1.3
Die maximale Höhe der Wasserrutsche im Intervall ![\([80;140]\)](https://www.schullv.de/resources/formulas/02c75aec44304a4a84ce37502eaeb31dcd8ebea98f3b73302af6ddc07bb937a5_light.svg) entspricht dem maximalen Funktionswert von
entspricht dem maximalen Funktionswert von  in diesem Intervall. Im CAS können die ersten beiden Ableitungen von
in diesem Intervall. Im CAS können die ersten beiden Ableitungen von  definiert werden.
definiert werden.
 Der Graph von
Der Graph von  besitzt somit an der Stelle
besitzt somit an der Stelle  einen Hochpunkt.
3. Schritt: Funktionswerte vergleichen
Vergleichen mit den Funktionswerten an den Rändern des Intervalls liefert:
einen Hochpunkt.
3. Schritt: Funktionswerte vergleichen
Vergleichen mit den Funktionswerten an den Rändern des Intervalls liefert:
![\([80;140]\)](https://www.schullv.de/resources/formulas/02c75aec44304a4a84ce37502eaeb31dcd8ebea98f3b73302af6ddc07bb937a5_light.svg) beträgt die maximale Höhe somit ca.
beträgt die maximale Höhe somit ca.  Maximales Gefälle bestimmen
Gesucht ist das maximale Gefälle, also der Funktionswert der Wendestelle von
Maximales Gefälle bestimmen
Gesucht ist das maximale Gefälle, also der Funktionswert der Wendestelle von  im Intervall
im Intervall ![\([80;140].\)](https://www.schullv.de/resources/formulas/1f8219025f02e975ea3eacbd1fdd4273aeb14aca3e68cf94838b1bc13ba15a11_light.svg) Die dritte Ableitung von
Die dritte Ableitung von  kann hierfür im CAS definiert werden.
kann hierfür im CAS definiert werden.
 3. Schritt: Funktionswerte vergleichen
Vergleichen mit den Randwerten des Intervalls liefert:
3. Schritt: Funktionswerte vergleichen
Vergleichen mit den Randwerten des Intervalls liefert:
 somit an der Stelle
somit an der Stelle  mit
mit  Das größte Gefälle im Intervall
Das größte Gefälle im Intervall ![\([80;140]\)](https://www.schullv.de/resources/formulas/02c75aec44304a4a84ce37502eaeb31dcd8ebea98f3b73302af6ddc07bb937a5_light.svg) beträgt damit ca.
beträgt damit ca. 
1. Schritt: Notwendige Bedingung für Extremstellen anwenden
Mit dem solve-Befehl des CAS ergibt sich:
![\(\begin{array}[t]{rll}
f](https://www.schullv.de/resources/formulas/50c43cd28ad371ea3e2272d62a80a52ac2be13c4b00adc8429ff5e9915a0e708_light.svg) Da der Hochpunkt im Intervall
Da der Hochpunkt im Intervall ![\([80;140]\)](https://www.schullv.de/resources/formulas/02c75aec44304a4a84ce37502eaeb31dcd8ebea98f3b73302af6ddc07bb937a5_light.svg) gesucht wird, ist die einzige mögliche Extremstelle
gesucht wird, ist die einzige mögliche Extremstelle  2. Schritt: Hinreichende Bedingung für Extremstellen anwenden
2. Schritt: Hinreichende Bedingung für Extremstellen anwenden


1. Schritt: Notwendige Bedingung für Wendestellen anwenden
Mit dem solve-Befehl des CAS ergibt sich:
![\(\begin{array}[t]{rll}
f](https://www.schullv.de/resources/formulas/09dd971e977b4d5e8e57c402e21db786f625820016be00667249d2f34bf77a25_light.svg) Da die Wendestelle im Intervall
Da die Wendestelle im Intervall ![\([80;140]\)](https://www.schullv.de/resources/formulas/02c75aec44304a4a84ce37502eaeb31dcd8ebea98f3b73302af6ddc07bb937a5_light.svg) liegen soll, ist
liegen soll, ist  die einzige mögliche Stelle.
2. Schritt: Hinreichende Bedingung für Extremstellen anwenden
die einzige mögliche Stelle.
2. Schritt: Hinreichende Bedingung für Extremstellen anwenden
 An der Stelle
An der Stelle  besitzt der Graph von
besitzt der Graph von  damit eine Wendestelle.
damit eine Wendestelle.

2.1
Die Bedingung „Knickfrei“ bedeutet, dass sich die Steigung der Rutschbahn nicht plötzlich verändert.
Ist dies an der Übergangsstelle nicht der Fall, so kann eine Sprungstelle der ersten Ableitung in zwei Varianten erfolgen:
- Das Gefälle vor dem Übergang kann größer als danach sein. Aufgrund von der schlagartigen Abnahme des Gefälles könnte das Schlauchboot mit der Vorderseite auf der Rutschbahn aufstoßen und abrupt abgebremst werden oder sogar stecken bleiben.
- Das Gefälle vor dem Übergang kann kleiner als danach sein und im Knick dann schlagartig in ein steileres Gefälle übergehen. Hier kann es passieren, dass das Schlauchboot für kurze Zeit den Kontakt zur Rutschbahn verliert und in freien Fall gerät. Beim erneuten Auftreffen könnte es sich dann beispielsweise überschlagen oder seitlich kippen, wobei die Personen in dem Schlauchboot verletzt werden könnten.
2.2
Damit der Übergangspunkt krümmungsruckfrei ist, muss der Graph der Funktion  dieselbe Krümmung wie der Graph der Funktion
dieselbe Krümmung wie der Graph der Funktion  besitzen, welche durch die zweite Abbildung der Funktionen beschrieben wird. Es muss also
besitzen, welche durch die zweite Abbildung der Funktionen beschrieben wird. Es muss also  gelten.
gelten.
2.3
Die beiden Funktionen müssen im Punkt  auf Sprungfreiheit, Knickfreiheit und Krümmungsruckfreiheit zum Graphen von
auf Sprungfreiheit, Knickfreiheit und Krümmungsruckfreiheit zum Graphen von  geprüft werden.
Mit dem CAS ergibt sich:
geprüft werden.
Mit dem CAS ergibt sich:
![\(\begin{array}[t]{rll}
f(15)&=& 25&\\[5pt]
f](https://www.schullv.de/resources/formulas/0503d906c0ab322b6b9375dd5b02ea50364fa90d546dcaf360882cd703bf903e_light.svg)
![\(\begin{array}[t]{rll}
g_A(15) &=& 25 \\[5pt]
g_A](https://www.schullv.de/resources/formulas/7e807d08b927e287cb575edc36d4a794a3d9b3d50b6e6329e75432b6e7285310_light.svg)
![\(\begin{array}[t]{rll}
g_B(15) &\approx& 25 \\[5pt]
g_B](https://www.schullv.de/resources/formulas/bacf7d35b80e10f4303745007cbf7c50e45b44b740f19635c00d7780db8d24c8_light.svg) Bei beiden Funktionen stimmen sowohl Funktionswert als auch der Wert der ersten Ableitungsfunktion näherungsweise mit den Werten von
Bei beiden Funktionen stimmen sowohl Funktionswert als auch der Wert der ersten Ableitungsfunktion näherungsweise mit den Werten von  überein. Die Graphen beider Funktionen verlaufen somit sprung- und knickfrei.
Der Wert der zweiten Ableitung weicht bei
überein. Die Graphen beider Funktionen verlaufen somit sprung- und knickfrei.
Der Wert der zweiten Ableitung weicht bei  im Gegensatz zu
im Gegensatz zu  deutlich von
deutlich von  ab. Die Krümmungsruckfreiheit ist für
ab. Die Krümmungsruckfreiheit ist für  folglich nicht gegeben, was im Punkt
folglich nicht gegeben, was im Punkt  zu einer abrupten Krümmungsänderung und somit zu einer schlagartigen Beschleunigung bzw. zu schlagartigem Abbremsen führen würde.
Die Funktion
zu einer abrupten Krümmungsänderung und somit zu einer schlagartigen Beschleunigung bzw. zu schlagartigem Abbremsen führen würde.
Die Funktion  ist somit besser zur Modellierung geeignet als die Funktion
ist somit besser zur Modellierung geeignet als die Funktion 
3
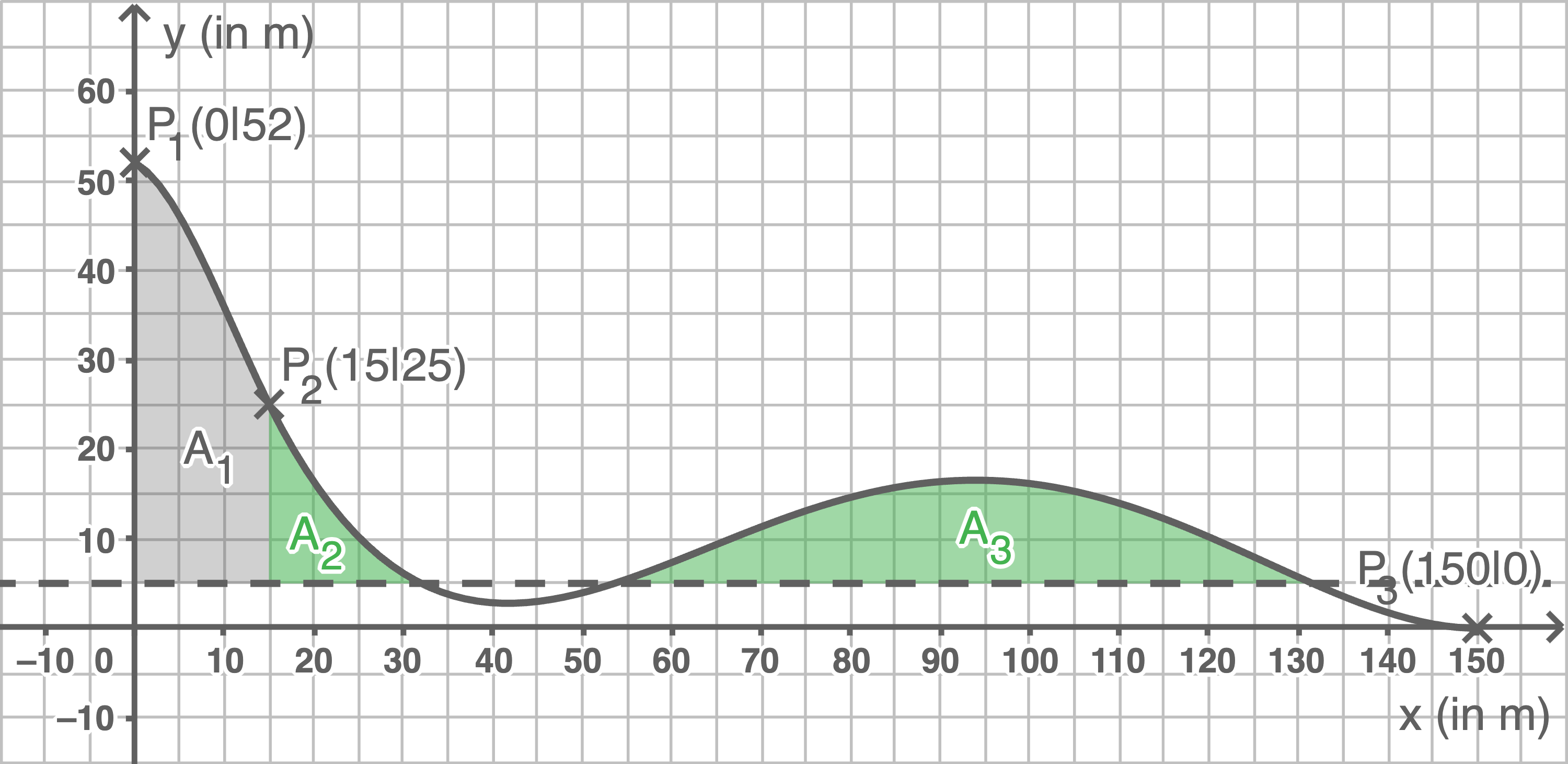
Hilfsskizze
