C - Stochastik
Eine Großbäckerei stellt Toastbrote mit einem (auf ganze Gramm gerundeten) Sollgewicht von  her. Bei
her. Bei  aller Brote tritt eine Abweichung vom Sollgewicht auf.
aller Brote tritt eine Abweichung vom Sollgewicht auf.
1.
Ein Einzelhändler im Gießener Umland erhält eine Lieferung von 50 Toastbroten.
1.1
Berechne, wie viele Brote mit einer Abweichung vom Sollgewicht der Einzelhändler erwarten kann, und erläutere, warum man die Prüfung der Toastbrote auf Abweichung vom Sollgewicht als Bernoullikette auffassen kann.
(3 BE)
1.2
Bestimme jeweils die Wahrscheinlichkeit folgender Ereignisse:
A: In der Lieferung weisen mehr als 4 Brote eine Abweichung vom Sollgewicht auf.
B: In der Lieferung weisen mindestens 47 Brote keine Abweichung vom Sollgewicht auf.
(5 BE)
2.
Ein Hersteller von Teigportioniermaschinen möchte der Großbäckerei eine neue Maschine verkaufen. Um festzustellen, ob die neue Maschine zuverlässiger ist als die alte, werden beide Maschinen empirisch überprüft.
Die Verteilungen für das tatsächliche (auf ganze Gramm gerundete) Brotgewicht  sind in den folgenden Tabellen zu sehen. Bei der alten Maschine betragen der Erwartungswert
sind in den folgenden Tabellen zu sehen. Bei der alten Maschine betragen der Erwartungswert  und die Standardabweichung
und die Standardabweichung  .
alte Maschine
.
alte Maschine
neue Maschine
Berechne für die neue Maschine den Erwartungswert und die Standardabweichung von  und beurteile aufgrund dieser Ereignisse, ob die Anschaffung der neuen Maschine eine Verbesserung in Bezug auf die Einhaltung des Sollgewichts bewirken würde.
und beurteile aufgrund dieser Ereignisse, ob die Anschaffung der neuen Maschine eine Verbesserung in Bezug auf die Einhaltung des Sollgewichts bewirken würde.
| Gewicht in |
Anteil Brote |
|---|---|
| Gewicht in |
Anteil Brote |
|---|---|
(7 BE)
3.
Bei der Überprüfung der Verpackungsmaschine stellt sich heraus, dass  der Brote nicht ordnungsgemäß verpackt werden. Die Warenausgangskontrolle lässt mit einer Wahrscheinlichkeit von
der Brote nicht ordnungsgemäß verpackt werden. Die Warenausgangskontrolle lässt mit einer Wahrscheinlichkeit von  ein fehlerhaft verpacktes Brot passieren und sortiert mit einer Wahrscheinlichkeit von
ein fehlerhaft verpacktes Brot passieren und sortiert mit einer Wahrscheinlichkeit von  ein ordnungsgemäß verpacktes Brot fälschlicherweise aus.
ein ordnungsgemäß verpacktes Brot fälschlicherweise aus.
3.1
Stelle diesen Sachverhalt in einem Baumdiagramm oder einer Vierfeldertafel dar.
(4 BE)
3.2
Berechne die Wahrscheinlichkeit, dass die Verpackung eines aussortierten Brotes tatsächlich fehlerhaft ist.
(4 BE)
3.3
Seit einiger Zeit häufen sich die Reklamationen wegen fehlerhafter Verpackungen. Daraufhin lässt die Großbäckerei die Verpackungsmaschine genauer untersuchen und testet die Nullhypothese  .
Bei einer Stichprobe von 100 Broten werden vier fehlerhaft verpackte Brote gefunden. Die Nullhypothese wird daraufhin nicht verworfen.
Prüfe auf einem Signifikanzniveau von
.
Bei einer Stichprobe von 100 Broten werden vier fehlerhaft verpackte Brote gefunden. Die Nullhypothese wird daraufhin nicht verworfen.
Prüfe auf einem Signifikanzniveau von  , ob diese Entscheidung gerechtfertigt ist.
, ob diese Entscheidung gerechtfertigt ist.
(7 BE)
1.1
Erwartungswert berechnen
Der Aufgabenstellung können die Anzahl der gelieferten Toastbrote sowie die Wahrscheinlichkeit für Brote mit einer Abweichung vom Sollgewicht entnommen werden:
 und
und  Somit gilt für den Erwartungswert
Somit gilt für den Erwartungswert  :
:
![\(\begin{array}[t]{rll}
\mu&=& p \cdot n \\[5pt]
&=& 0,02 \cdot 50 \\[5pt]
&=& 1
\end{array}\)](https://www.schullv.de/resources/formulas/4695d339170a03d331ddf1d534adab567a79c6ca92d99daddc28d64591b3e85c_light.svg) Der Einzelhändler kann erwarten, dass von den 50 gelieferten Toastbroten 1 Toastbrot vom Sollgewicht abweicht.
Aufassung als Bernoullikette erläutern
Bei einer Bernoullikette gibt es nur zwei mögliche Ereignisse. Dies ist bei der Prüfung der Toastbrote auch der Fall, da ein Toastbrot entweder dem Sollgewicht entspricht oder davon abweicht.
Außerdem muss gelten, dass die einzelnen Ereignisse stochastisch unabhängig voneinander sind. Da sich hier die Wahrscheinlichkeit dafür, dass ein Toastbrot vom Sollgewicht abweicht, nicht ändert, kann die Prüfung der Toastbrote folglich als Bernoullikette aufgefasst werden.
Der Einzelhändler kann erwarten, dass von den 50 gelieferten Toastbroten 1 Toastbrot vom Sollgewicht abweicht.
Aufassung als Bernoullikette erläutern
Bei einer Bernoullikette gibt es nur zwei mögliche Ereignisse. Dies ist bei der Prüfung der Toastbrote auch der Fall, da ein Toastbrot entweder dem Sollgewicht entspricht oder davon abweicht.
Außerdem muss gelten, dass die einzelnen Ereignisse stochastisch unabhängig voneinander sind. Da sich hier die Wahrscheinlichkeit dafür, dass ein Toastbrot vom Sollgewicht abweicht, nicht ändert, kann die Prüfung der Toastbrote folglich als Bernoullikette aufgefasst werden.
1.2
Ereignis 
 beschreibt die Anzahl der Toastbrote, die eine Abweichung vom Sollgewicht aufweisen, und ist binomialverteilt mit
beschreibt die Anzahl der Toastbrote, die eine Abweichung vom Sollgewicht aufweisen, und ist binomialverteilt mit  und
und  Es gilt:
Es gilt:  Mit dem CAS ergibt sich für
Mit dem CAS ergibt sich für  :
:
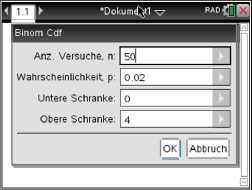
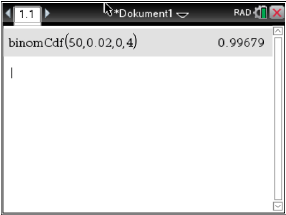 Es folgt also:
Es folgt also:
![\(\begin{array}[t]{rll}
P(X\gt 4)&=& 1- P(X \leq 4)& \quad \scriptsize \mid CAS \\[5pt]
&\approx& 1- 0,99679 & \\[5pt]
&=& 0,00321 & \\[5pt]
&\approx& 0,3 \,\% & \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/ede4d454078a4814f13173349a69b44cf64e7fc3d83f10e1ce9490ebdcc91021_light.svg) Somit tritt das Ereignis
Somit tritt das Ereignis  mit einer Wahrscheinlichkeit von etwa
mit einer Wahrscheinlichkeit von etwa  auf.
Ereignis
auf.
Ereignis 
 beschreibt die Anzahl der Toastbrote, die keine Abweichung vom Sollgewicht aufweisen, und ist binomialverteilt mit
beschreibt die Anzahl der Toastbrote, die keine Abweichung vom Sollgewicht aufweisen, und ist binomialverteilt mit  und
und  Analog zu Ereignis
Analog zu Ereignis  ergibt sich:
ergibt sich:
![\(\begin{array}[t]{rll}
P(Y \geq 47)&=& 1- P(Y \lt 47 )& \\[5pt]
&=& 1- P(Y \leq 46 )&\quad \scriptsize \mid\; CAS \\[5pt]
&\approx & 1- 0,01775&\\[5pt]
&= & 0,98225& \\[5pt]
&\approx & 98,2\,\% & \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/a0b644902da6f41fcd18c724908b15323c698aaefa04a850ccaa12d8c4593757_light.svg) Somit tritt Ereignis
Somit tritt Ereignis  mit einer Wahrscheinlichkeit von etwa
mit einer Wahrscheinlichkeit von etwa  auf.
auf.
5: Wahrscheinlichkeit  5: Verteilungen
5: Verteilungen  D: Binomial Cdf
D: Binomial Cdf


2.
Erwartungswert bestimmen
Für den Erwartungswert des Brotgewichts mit der neuen Maschine gilt:
Der Erwartungswert der neuen Maschine beträgt somit  .
Standardabweichung bestimmen
Die Standardabweichung lässt sich anhand der Varianz wie folgt berechnen:
.
Standardabweichung bestimmen
Die Standardabweichung lässt sich anhand der Varianz wie folgt berechnen:  Varianz
Varianz  berechnen:
Die Standardabweichung
berechnen:
Die Standardabweichung  folgt nun mit:
folgt nun mit:
![\(\begin{array}[t]{rll}
\sigma_{\text{Neu}}(Y)&=&\sqrt{\text{Var}(Y)} \\[5pt]
&=& \sqrt{0,04\text{ g}^2} \\[5pt]
&=& 0,2 \text{g}
\end{array}\)](https://www.schullv.de/resources/formulas/6d867e2d51de438c3e6659b638f689fdcaee38295430903c12ed603ef5976c8e_light.svg) Somit beträgt die Standardabweichung für die neue Maschine
Somit beträgt die Standardabweichung für die neue Maschine  Neue Maschine beurteilen
Der Erwartungswert der beiden Maschinen ist identisch und liegt bei
Neue Maschine beurteilen
Der Erwartungswert der beiden Maschinen ist identisch und liegt bei  . Die Standardabweichung beträgt bei der alten Maschine
. Die Standardabweichung beträgt bei der alten Maschine  und bei der neuen Maschine
und bei der neuen Maschine  .
Da die Standardabweichung bei der neuen Maschine geringer als bei der alten Maschine ist, würde das Gewicht des Toastbrots mit der neuen Maschine also nicht mehr so stark vom Sollgewicht abweichen.
Die Anschaffung einer neuen Maschine würde somit eine Verbesserung in Bezug auf die Einhaltung des Sollgewichts bewirken.
.
Da die Standardabweichung bei der neuen Maschine geringer als bei der alten Maschine ist, würde das Gewicht des Toastbrots mit der neuen Maschine also nicht mehr so stark vom Sollgewicht abweichen.
Die Anschaffung einer neuen Maschine würde somit eine Verbesserung in Bezug auf die Einhaltung des Sollgewichts bewirken.
3.1
Aus der Aufgabenstellung können einige Wahrscheinlichkeiten bereits entnommen werden:



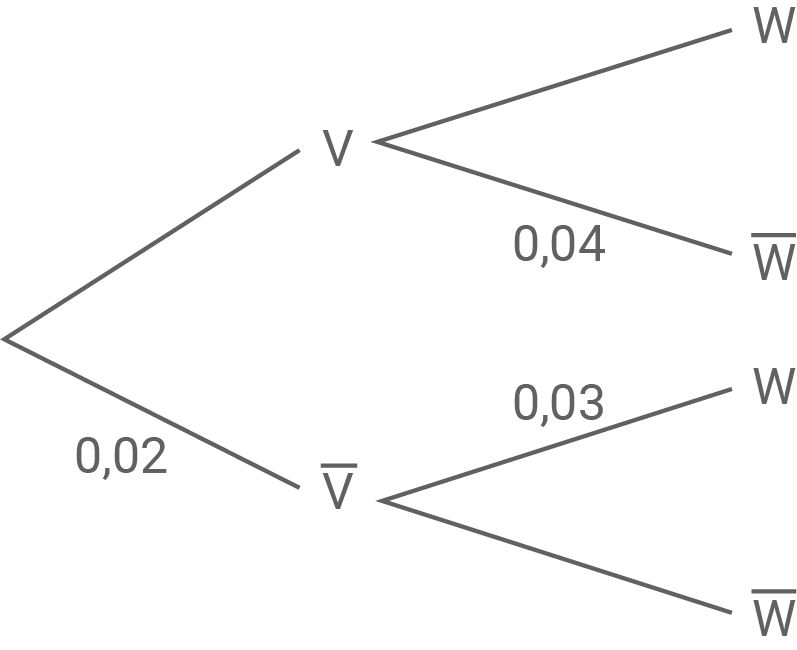
Die fehlenden Wahrscheinlichkeiten können nun durch die Gegenereignisse berechnet werden:



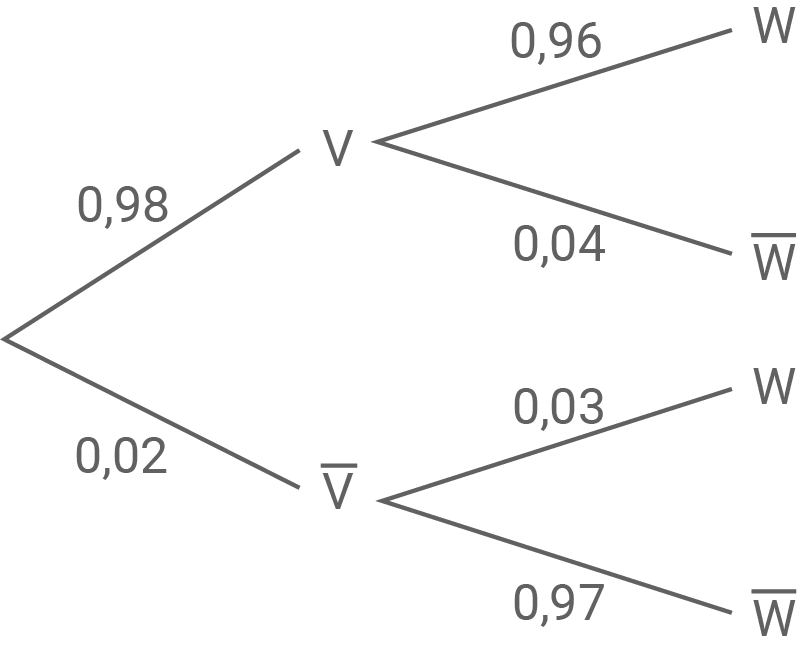
3.2
Gesucht ist die bedingte Wahrscheinlichkeit  .
Mit dem Satz von Bayes ergibt sich:
.
Mit dem Satz von Bayes ergibt sich:
![\(\begin{array}[t]{rll}
P_{\overline{W}}(\overline{V})&=&\dfrac{P_{\overline{V}}(\overline{W})\cdot P(\overline{V})}{P(\overline{W})} & \\[5pt]
&=& \dfrac{0,97 \cdot 0,02}{0,98\cdot 0,04+0,02\cdot 0,97}& \\[5pt]
&=& \dfrac{0,97 \cdot 0,02}{0,586}& \\[5pt]
&\approx& 0,3311& \\[5pt]
&=& 33,11 \,\% & \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/a6673fef5dfcc3532d17a72076362515de06a992747a4ac338009ed80244ca11_light.svg) Somit beträgt die Wahrscheinlichkeit dafür, dass die Verpackung eines aussortierten Brotes tatsächlich fehlerhaft ist,
Somit beträgt die Wahrscheinlichkeit dafür, dass die Verpackung eines aussortierten Brotes tatsächlich fehlerhaft ist,  .
.
3.3
Die Zufallsvariable  beschreibt die Anzahl der fehlerhaft verpackten Brote und ist binomialverteilt mit
beschreibt die Anzahl der fehlerhaft verpackten Brote und ist binomialverteilt mit  Es soll ein rechtsseitiger Hypothesentest mit der Nullhypothese
Es soll ein rechtsseitiger Hypothesentest mit der Nullhypothese  durchgeführt werden:
Der Ablehnungsbereich ist definiert als
durchgeführt werden:
Der Ablehnungsbereich ist definiert als  Es soll also gelten:
Es soll also gelten:
![\(\begin{array}[t]{rll}
P(X\geq k)&\leq& 5 \,\% & \\[5pt]
1- &\leq& 0,05 & \\[5pt]
P(X\leq k-1)&\geq& 0,95& \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/5bbf7ad76c12a4a4435753913d7d30e885408d736fe1836af0e2932a07574b10_light.svg) Aus der Tabelle folgt:
Aus der Tabelle folgt:

 .
Somit folgt für den Ablehungsbereich:
.
Somit folgt für den Ablehungsbereich:
![\(\begin{array}[t]{rll}
\overline{A}&=& {5+1,\dotsc ,100}& \\[5pt]
&=&{6,\dotsc ,100}
\end{array}\)](https://www.schullv.de/resources/formulas/faa3081d63d962894cb7a6a136152f0838117abccf2632b6ecc07cbc995a8768_light.svg) Da nur 4 fehlerhafte Verpackungen vorliegen, wird die Nullhypothese nicht verworfen und die Entscheidung ist somit gerechtfertigt.
Da nur 4 fehlerhafte Verpackungen vorliegen, wird die Nullhypothese nicht verworfen und die Entscheidung ist somit gerechtfertigt.
1.1
Erwartungswert berechnen
Der Aufgabenstellung können die Anzahl der gelieferten Toastbrote sowie die Wahrscheinlichkeit für Brote mit einer Abweichung vom Sollgewicht entnommen werden:
 und
und  Somit gilt für den Erwartungswert
Somit gilt für den Erwartungswert  :
:
![\(\begin{array}[t]{rll}
\mu&=& p \cdot n \\[5pt]
&=& 0,02 \cdot 50 \\[5pt]
&=& 1
\end{array}\)](https://www.schullv.de/resources/formulas/4695d339170a03d331ddf1d534adab567a79c6ca92d99daddc28d64591b3e85c_light.svg) Der Einzelhändler kann erwarten, dass von den 50 gelieferten Toastbroten 1 Toastbrot vom Sollgewicht abweicht.
Aufassung als Bernoullikette erläutern
Bei einer Bernoullikette gibt es nur zwei mögliche Ereignisse. Dies ist bei der Prüfung der Toastbrote auch der Fall, da ein Toastbrot entweder dem Sollgewicht entspricht oder davon abweicht.
Außerdem muss gelten, dass die einzelnen Ereignisse stochastisch unabhängig voneinander sind. Da sich hier die Wahrscheinlichkeit dafür, dass ein Toastbrot vom Sollgewicht abweicht, nicht ändert, kann die Prüfung der Toastbrote folglich als Bernoullikette aufgefasst werden.
Der Einzelhändler kann erwarten, dass von den 50 gelieferten Toastbroten 1 Toastbrot vom Sollgewicht abweicht.
Aufassung als Bernoullikette erläutern
Bei einer Bernoullikette gibt es nur zwei mögliche Ereignisse. Dies ist bei der Prüfung der Toastbrote auch der Fall, da ein Toastbrot entweder dem Sollgewicht entspricht oder davon abweicht.
Außerdem muss gelten, dass die einzelnen Ereignisse stochastisch unabhängig voneinander sind. Da sich hier die Wahrscheinlichkeit dafür, dass ein Toastbrot vom Sollgewicht abweicht, nicht ändert, kann die Prüfung der Toastbrote folglich als Bernoullikette aufgefasst werden.
1.2
Ereignis 
 beschreibt die Anzahl der Toastbrote, die eine Abweichung vom Sollgewicht aufweisen, und ist binomialverteilt mit
beschreibt die Anzahl der Toastbrote, die eine Abweichung vom Sollgewicht aufweisen, und ist binomialverteilt mit  und
und  Es gilt:
Es gilt:  Mit dem CAS ergibt sich für
Mit dem CAS ergibt sich für  :
:
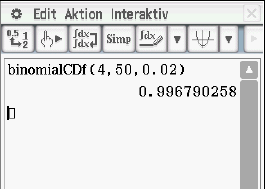 Es folgt also:
Es folgt also:
![\(\begin{array}[t]{rll}
P(X\gt 4)&=& 1- P(X \leq 4)& \quad \scriptsize \mid CAS \\[5pt]
&\approx& 1- 0,99679 & \\[5pt]
&=& 0,00321 & \\[5pt]
&\approx& 0,3 \,\% & \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/ede4d454078a4814f13173349a69b44cf64e7fc3d83f10e1ce9490ebdcc91021_light.svg) Somit tritt das Ereignis
Somit tritt das Ereignis  mit einer Wahrscheinlichkeit von etwa
mit einer Wahrscheinlichkeit von etwa  auf.
Ereignis
auf.
Ereignis 
 beschreibt die Anzahl der Toastbrote, die keine Abweichung vom Sollgewicht aufweisen, und ist binomialverteilt mit
beschreibt die Anzahl der Toastbrote, die keine Abweichung vom Sollgewicht aufweisen, und ist binomialverteilt mit  und
und  Analog zu Ereignis
Analog zu Ereignis  ergibt sich:
ergibt sich:
![\(\begin{array}[t]{rll}
P(Y \geq 47)&=& 1- P(Y \lt 47 )& \\[5pt]
&=& 1- P(Y \leq 46 )&\quad \scriptsize \mid\; CAS \\[5pt]
&\approx & 1- 0,01775&\\[5pt]
&= & 0,98225& \\[5pt]
&\approx & 98,2\,\% & \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/a0b644902da6f41fcd18c724908b15323c698aaefa04a850ccaa12d8c4593757_light.svg) Somit tritt Ereignis
Somit tritt Ereignis  mit einer Wahrscheinlichkeit von etwa
mit einer Wahrscheinlichkeit von etwa  auf.
auf.
Aktion  Verteilungsfunktionen
Verteilungsfunktionen  Diskret
Diskret  binomialCDf
binomialCDf

2.
Erwartungswert bestimmen
Für den Erwartungswert des Brotgewichts mit der neuen Maschine gilt:
Der Erwartungswert der neuen Maschine beträgt somit  .
Standardabweichung bestimmen
Die Standardabweichung lässt sich anhand der Varianz wie folgt berechnen:
.
Standardabweichung bestimmen
Die Standardabweichung lässt sich anhand der Varianz wie folgt berechnen:  Varianz
Varianz  berechnen:
Die Standardabweichung
berechnen:
Die Standardabweichung  folgt nun mit:
folgt nun mit:
![\(\begin{array}[t]{rll}
\sigma_{\text{Neu}}(Y)&=&\sqrt{\text{Var}(Y)} \\[5pt]
&=& \sqrt{0,04\text{ g}^2} \\[5pt]
&=& 0,2 \text{g}
\end{array}\)](https://www.schullv.de/resources/formulas/6d867e2d51de438c3e6659b638f689fdcaee38295430903c12ed603ef5976c8e_light.svg) Somit beträgt die Standardabweichung für die neue Maschine
Somit beträgt die Standardabweichung für die neue Maschine  Neue Maschine beurteilen
Der Erwartungswert der beiden Maschinen ist identisch und liegt bei
Neue Maschine beurteilen
Der Erwartungswert der beiden Maschinen ist identisch und liegt bei  . Die Standardabweichung beträgt bei der alten Maschine
. Die Standardabweichung beträgt bei der alten Maschine  und bei der neuen Maschine
und bei der neuen Maschine  .
Da die Standardabweichung bei der neuen Maschine geringer als bei der alten Maschine ist, würde das Gewicht des Toastbrots mit der neuen Maschine also nicht mehr so stark vom Sollgewicht abweichen.
Die Anschaffung einer neuen Maschine würde somit eine Verbesserung in Bezug auf die Einhaltung des Sollgewichts bewirken.
.
Da die Standardabweichung bei der neuen Maschine geringer als bei der alten Maschine ist, würde das Gewicht des Toastbrots mit der neuen Maschine also nicht mehr so stark vom Sollgewicht abweichen.
Die Anschaffung einer neuen Maschine würde somit eine Verbesserung in Bezug auf die Einhaltung des Sollgewichts bewirken.
3.1
Aus der Aufgabenstellung können einige Wahrscheinlichkeiten bereits entnommen werden:




Die fehlenden Wahrscheinlichkeiten können nun durch die Gegenereignisse berechnet werden:




3.2
Gesucht ist die bedingte Wahrscheinlichkeit  .
Mit dem Satz von Bayes ergibt sich:
.
Mit dem Satz von Bayes ergibt sich:
![\(\begin{array}[t]{rll}
P_{\overline{W}}(\overline{V})&=&\dfrac{P_{\overline{V}}(\overline{W})\cdot P(\overline{V})}{P(\overline{W})} & \\[5pt]
&=& \dfrac{0,97 \cdot 0,02}{0,98\cdot 0,04+0,02\cdot 0,97}& \\[5pt]
&=& \dfrac{0,97 \cdot 0,02}{0,586}& \\[5pt]
&\approx& 0,3311& \\[5pt]
&=& 33,11 \,\% & \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/a6673fef5dfcc3532d17a72076362515de06a992747a4ac338009ed80244ca11_light.svg) Somit beträgt die Wahrscheinlichkeit dafür, dass die Verpackung eines aussortierten Brotes tatsächlich fehlerhaft ist,
Somit beträgt die Wahrscheinlichkeit dafür, dass die Verpackung eines aussortierten Brotes tatsächlich fehlerhaft ist,  .
.
3.3
Die Zufallsvariable  beschreibt die Anzahl der fehlerhaft verpackten Brote und ist binomialverteilt mit
beschreibt die Anzahl der fehlerhaft verpackten Brote und ist binomialverteilt mit  Es soll ein rechtsseitiger Hypothesentest mit der Nullhypothese
Es soll ein rechtsseitiger Hypothesentest mit der Nullhypothese  durchgeführt werden:
Der Ablehnungsbereich ist definiert als
durchgeführt werden:
Der Ablehnungsbereich ist definiert als  Es soll also gelten:
Es soll also gelten:
![\(\begin{array}[t]{rll}
P(X\geq k)&\leq& 5 \,\% & \\[5pt]
1- &\leq& 0,05 & \\[5pt]
P(X\leq k-1)&\geq& 0,95& \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/5bbf7ad76c12a4a4435753913d7d30e885408d736fe1836af0e2932a07574b10_light.svg) Aus der Tabelle folgt:
Aus der Tabelle folgt:

 .
Somit folgt für den Ablehungsbereich:
.
Somit folgt für den Ablehungsbereich:
![\(\begin{array}[t]{rll}
\overline{A}&=& {5+1,\dotsc ,100}& \\[5pt]
&=&{6,\dotsc ,100}
\end{array}\)](https://www.schullv.de/resources/formulas/faa3081d63d962894cb7a6a136152f0838117abccf2632b6ecc07cbc995a8768_light.svg) Da nur 4 fehlerhafte Verpackungen vorliegen, wird die Nullhypothese nicht verworfen und die Entscheidung ist somit gerechtfertigt.
Da nur 4 fehlerhafte Verpackungen vorliegen, wird die Nullhypothese nicht verworfen und die Entscheidung ist somit gerechtfertigt.