A2 - Analysis
Eine Gärtnerei vertreibt ein tunnelförmiges Foliengewächshaus, dessen Bodenfläche  lang und
lang und  breit ist und dessen Höhe
breit ist und dessen Höhe  beträgt (Material 1).
beträgt (Material 1).
 Material 2
Material 2
 Material 3
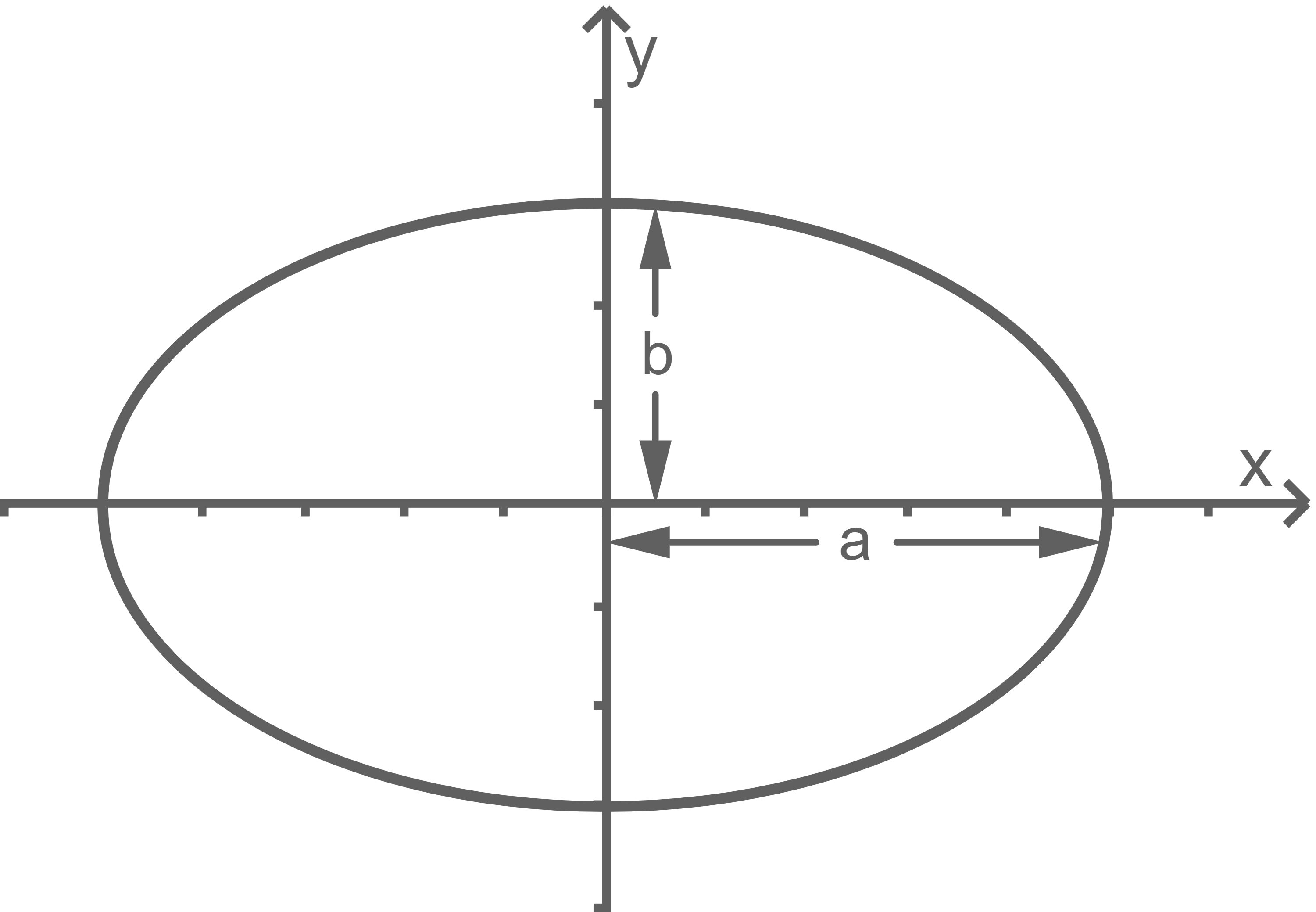
Information: Die Gleichung
Material 3
Information: Die Gleichung  beschreibt eine Ellipse, deren Mittelpunkt im Nullpunkt des Koordinatensystems liegt und deren große Halbachse mit
beschreibt eine Ellipse, deren Mittelpunkt im Nullpunkt des Koordinatensystems liegt und deren große Halbachse mit  die kleine Halbachse mit
die kleine Halbachse mit  bezeichnet wird
bezeichnet wird
1.
Ermittle die Funktionsgleichung einer quadratischen Funktion  deren Graph die parabelförmige Berandung der vorderen Abschlussfläche des Gewächshauses beschreibt.
deren Graph die parabelförmige Berandung der vorderen Abschlussfläche des Gewächshauses beschreibt.
(6 BE)
2.1
Berechne das gesamte Volumen des Gewächshauses unter der Annahme, dass die vordere und hintere Abschlussfläche senkrecht auf der Bodenfläche stehen.
(8 BE)
2.2
Um eine geeignete Arbeitshöhe für die Gärtner zu bekommen, wird in einer Hälfte des Gewächshauses in 1 Meter Höhe über die gesamte Länge des Gewächshauses ein Zwischenboden eingefügt (Material 2).
Ermittle den Flächeninhalt des Zwischenbodens.
Berechne, um wie viel Prozent der Zwischenboden kleiner ist als die Bodenfläche dieser Gewächshaushälfte.
Ermittle den Flächeninhalt des Zwischenbodens.
Berechne, um wie viel Prozent der Zwischenboden kleiner ist als die Bodenfläche dieser Gewächshaushälfte.
(6 BE)
3.
Im Zusammenhang mit dem Gewächshaus wird der folgende Term aufgestellt.

Erläutere mit Hilfe der Information im untenstehenden Kasten den Aufbau dieses Terms und seine Bedeutung im Sachzusammenhang. Die Länge des Graphen einer differenzierbaren Funktion zwischen den Punkten
zwischen den Punkten  und
und  wird durch die folgende Formel berechnet:
wird durch die folgende Formel berechnet:


Erläutere mit Hilfe der Information im untenstehenden Kasten den Aufbau dieses Terms und seine Bedeutung im Sachzusammenhang. Die Länge des Graphen einer differenzierbaren Funktion
(6 BE)
4.
Mehrere Kunden reklamieren, dass das Gewächshaus im oberen Bereich zu eng gebaut sei. Die Firma möchte mit einer elliptischen Form Abhilfe schaffen (Material 3).
4.1
Die ursprüngliche Höhe und die Breite der Bodenfläche des Gewächshauses sollen zunächst beibehalten werden.
Bestimme eine entsprechende Funktion für das Profil des Gewächshauses und skizziere sie in Material 2.
für das Profil des Gewächshauses und skizziere sie in Material 2.
Bestimme eine entsprechende Funktion
(4 BE)
4.2
Allerdings wird der Verbrauch an Folie für die Bedachung jetzt größer. Die Firma möchte den Mehrverbrauch auf  gegenüber der parabelförmigen Bedachung beschränken und dafür die Höhe des Gewächshauses bei gleichbleibender Länge und Breite der Bodenfläche reduzieren. (Die vordere und hintere Abschlussfläche werden nicht betrachtet.)
gegenüber der parabelförmigen Bedachung beschränken und dafür die Höhe des Gewächshauses bei gleichbleibender Länge und Breite der Bodenfläche reduzieren. (Die vordere und hintere Abschlussfläche werden nicht betrachtet.)
Ermittle die dafür notwendige Höhenreduzierung unter Verwendung der in Aufgabe 3 gegebenen Formel.
Material 1
Ermittle die dafür notwendige Höhenreduzierung unter Verwendung der in Aufgabe 3 gegebenen Formel.
(10 BE)



Löst man die Gleichung nach y auf, erhält man für die Funktion des oberen Ellipsenbogens die Funktionsgleichung:

1.
Mit Hilfe der  -Achse als Boden und der
-Achse als Boden und der  -Achse in der Mitte des Durchschnittes des Gewächshaueses, wobei eine Längeneinheit einem Meter entspricht, ergeben sich aus der Aufgabenstellung folgende drei Gleichungen für die allgemeine Funktionsgleichung
-Achse in der Mitte des Durchschnittes des Gewächshaueses, wobei eine Längeneinheit einem Meter entspricht, ergeben sich aus der Aufgabenstellung folgende drei Gleichungen für die allgemeine Funktionsgleichung 
![\(\begin{array}[t]{rll}
p\left(-\dfrac{7}{2}\right)&=& 0 \\[5pt]
p\left(\dfrac{7}{2}\right)&=& 0 \\[5pt]
p(0)&=& 3
\end{array}\)](https://www.schullv.de/resources/formulas/1205525684115f965b8c62afe5cccebadd0140c60198df19e37401df1ce67b83_light.svg) Aufstellen eines linearen Gleichungssystems liefert:
Aufstellen eines linearen Gleichungssystems liefert:
 Lösen des Gleichungssystems mit dem CAS liefert:
Lösen des Gleichungssystems mit dem CAS liefert:
_2015_a2_l1b1_ti.png) Die Funktion
Die Funktion  ist also gegeben durch
ist also gegeben durch 






 wobei
wobei  im Intervall
im Intervall ![\([-3,5 ; 3,5]\)](https://www.schullv.de/resources/formulas/69ea26ba6b7002420ca768d0eb7c5ab083fcf226e4091353238e9069e4d5811a_light.svg) liegt und eine Längeneinheit einem Meter entspricht.
liegt und eine Längeneinheit einem Meter entspricht.
_2015_a2_l1b1_ti.png)
2.1
Das gesamte Volumen des Gewächshauses ergibt sich durch Multiplikation des Flächeninhaltes der Vorderfläche mit der Länge des Gewächshauses. Für den Flächeninhalt der Vorderfläche ergibt sich mit Hilfe der Integralberechnung des CAS unter 4: Analysis  3: Integral:
3: Integral:
![\(A = \displaystyle \int_{-3,5}^{3,5} p(x)\; \mathrm dx = 14 \;[\text{m}^2]\)](https://www.schullv.de/resources/formulas/1f2fb92a2883d119652f3ff522ba5ca3bd0cd8fbeb74548aa40ee0fe38e210f2_light.svg)
_2015_a2_l1b2_ti.png) Damit folgt für das gesamte Volumen des Gewächshauses:
Damit folgt für das gesamte Volumen des Gewächshauses:





![\( = 168 \;[\text{m}^3]\)](https://www.schullv.de/resources/formulas/9145f6518a2705086ca8c13d0db6df3b2ff7fbc7278e513100f6102c68eacc9c_light.svg)
_2015_a2_l1b2_ti.png)
2.2
1. Schritt: Fläche des Zwischenbodens berechnen
Die Fläche des Zwischenbodens hat die Form eines Rechtecks. Die Breite ergibt sich durch den  -Wert der in Material 2 dargestellten Schnittstelle der Geraden
-Wert der in Material 2 dargestellten Schnittstelle der Geraden  mit der Parabel. Mit Hilfe des solve-Befehls des CAS folgt für die Schnittstelle:
mit der Parabel. Mit Hilfe des solve-Befehls des CAS folgt für die Schnittstelle:

_2015_a2_l1b3_ti.png) Da der Zwischenboden in der Skizze rechts von der
Da der Zwischenboden in der Skizze rechts von der  -Achse liegt, ist
-Achse liegt, ist  die gesuchte
die gesuchte  -Koordinate. Für die Breite folgt:
-Koordinate. Für die Breite folgt:



![\( \approx 2,86 \;[\text{m}]\)](https://www.schullv.de/resources/formulas/f2e7c379bccc3c306903229b4710e7d518eb69c57fc9e77ecb7433e7dbeb2219_light.svg) .
Für den Flächeninhalt des Zwischenbodens folgt damit insgesamt:
.
Für den Flächeninhalt des Zwischenbodens folgt damit insgesamt:






![\( \approx 34,3 \;[\text{m}^2].\)](https://www.schullv.de/resources/formulas/f3f2f5b9f9d32620675542c491fb0e4fd9fc9b208a6052ed906bcdb2ba409422_light.svg) 2. Schritt: Flächeninhalt der Bodenfläche der Gewächshaushälfte berechnen
Mit einer Länge von
2. Schritt: Flächeninhalt der Bodenfläche der Gewächshaushälfte berechnen
Mit einer Länge von  und einer Breite von
und einer Breite von  folgt für den Flächeninhalt der Bodenflächenhälfte:
folgt für den Flächeninhalt der Bodenflächenhälfte:



 3. Schritt: Prozentuale Abweichung berechnen
3. Schritt: Prozentuale Abweichung berechnen


 Der Zwischenbodenflächeninhalt misst damit ca.
Der Zwischenbodenflächeninhalt misst damit ca.  der Bodenfläche der Gewächshaushälfte. Somit ist der Zwischenboden etwa
der Bodenfläche der Gewächshaushälfte. Somit ist der Zwischenboden etwa  kleiner.
kleiner.
_2015_a2_l1b3_ti.png)
3.
Einsetzen von  in die Formel aus der Aufgabenstellung zur Berechnung von
in die Formel aus der Aufgabenstellung zur Berechnung von  ergibt mit
ergibt mit  und
und  Das Integral ist somit also die Länge des Graphen zwischen dem Hochpunkt und der positiven Nullstelle von
Das Integral ist somit also die Länge des Graphen zwischen dem Hochpunkt und der positiven Nullstelle von  Die
Die  in dem Term entspricht der Länge des Gewächshauses, das heißt durch Multiplikation ergibt sich die Fläche der rechten Hälfte Gewächshausdaches. Multiplikation mit
in dem Term entspricht der Länge des Gewächshauses, das heißt durch Multiplikation ergibt sich die Fläche der rechten Hälfte Gewächshausdaches. Multiplikation mit  liefert die Fläche des gesamten Daches. Der Term becshreibt also die Fläche des Gewächshausdaches.
liefert die Fläche des gesamten Daches. Der Term becshreibt also die Fläche des Gewächshausdaches.
4.1
Funktion  bestimmen
Bei der allgemeinen Gleichung
bestimmen
Bei der allgemeinen Gleichung 

 einer Funktion für den oberen Ellipsenbogen entspricht
einer Funktion für den oberen Ellipsenbogen entspricht  der Höhe des Gewächshauses und
der Höhe des Gewächshauses und  der Breite. Einsetzen von
der Breite. Einsetzen von  und
und  liefert:
liefert:






 Funktion
Funktion  skizzieren
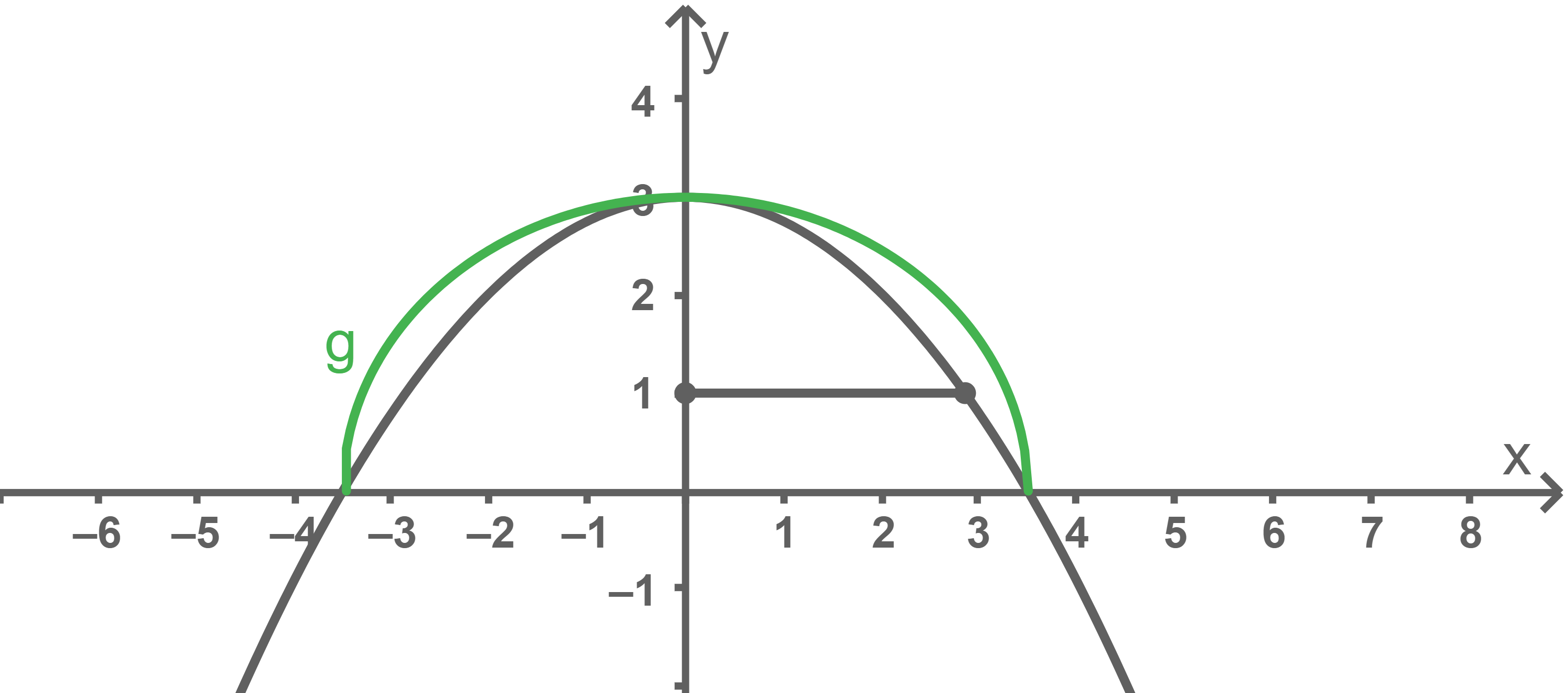
Mit Hilfe der Wertetabelle der Funktion
skizzieren
Mit Hilfe der Wertetabelle der Funktion  die sich im CAS anzeigen lässt, folgt:
die sich im CAS anzeigen lässt, folgt:

4.2
Für die Gleichung von  folgt bei gleichbleibender Breite:
folgt bei gleichbleibender Breite:






 1. Schritt: Größe der neuen Fläche
Berechnung des Termes aus Aufgabe 3 für die alte Fläche und Multiplikation mit
1. Schritt: Größe der neuen Fläche
Berechnung des Termes aus Aufgabe 3 für die alte Fläche und Multiplikation mit  liefert für die Größe der neuen Fläche:
liefert für die Größe der neuen Fläche:






![\( \cdot 115,41 \approx 121,18 \;[\text{m}^2]\)](https://www.schullv.de/resources/formulas/8badf13f55389b23168d95b571ab42588fac77374a847ffe4f77cc75fa9af703_light.svg)
_2015_a2_l1b5_ti.png) 2. Schritt: Neue Höhe bestimmen
Definition der ersten Ableitung
2. Schritt: Neue Höhe bestimmen
Definition der ersten Ableitung  im CAS und Lösen der Gleichung
im CAS und Lösen der Gleichung  mit dem solve-Befehl des CAS liefert für die neue Höhe:
mit dem solve-Befehl des CAS liefert für die neue Höhe:

_2015_a2_l1b6_ti.png) Insgesamt beträgt damit die Höhendifferenz
Insgesamt beträgt damit die Höhendifferenz ![\(3\;\text{m}-2,9\;\text{m}=0,1\;[\text{m}].\)](https://www.schullv.de/resources/formulas/69e82c6efc322f43e93af8409f84924f5cdb6ecb616528696f39d24b661c601f_light.svg)
_2015_a2_l1b5_ti.png)
_2015_a2_l1b6_ti.png)
1.
Mit Hilfe der  -Achse als Boden und der
-Achse als Boden und der  -Achse in der Mitte des Durchschnittes des Gewächshaueses, wobei eine Längeneinheit einem Meter entspricht, ergeben sich aus der Aufgabenstellung folgende drei Gleichungen für die allgemeine Funktionsgleichung
-Achse in der Mitte des Durchschnittes des Gewächshaueses, wobei eine Längeneinheit einem Meter entspricht, ergeben sich aus der Aufgabenstellung folgende drei Gleichungen für die allgemeine Funktionsgleichung 
![\(\begin{array}[t]{rll}
p\left(-\dfrac{7}{2}\right)&=& 0 \\[5pt]
p\left(\dfrac{7}{2}\right)&=& 0 \\[5pt]
p(0)&=& 3
\end{array}\)](https://www.schullv.de/resources/formulas/1205525684115f965b8c62afe5cccebadd0140c60198df19e37401df1ce67b83_light.svg) Aufstellen eines linearen Gleichungssystems liefert:
Aufstellen eines linearen Gleichungssystems liefert:
 Lösen des Gleichungssystems mit dem CAS liefert:
Lösen des Gleichungssystems mit dem CAS liefert:
_2015_a2_l1b1_casio.png) Die Funktion
Die Funktion  ist also gegeben durch
ist also gegeben durch 






 wobei
wobei  im Intervall
im Intervall ![\([-3,5 ; 3,5]\)](https://www.schullv.de/resources/formulas/69ea26ba6b7002420ca768d0eb7c5ab083fcf226e4091353238e9069e4d5811a_light.svg) liegt und eine Längeneinheit einem Meter entspricht.
liegt und eine Längeneinheit einem Meter entspricht.
_2015_a2_l1b1_casio.png)
2.1
Das gesamte Volumen des Gewächshauses ergibt sich durch Multiplikation des Flächeninhaltes der Vorderfläche mit der Länge des Gewächshauses. Für den Flächeninhalt der Vorderfläche ergibt sich mit Hilfe der Integralberechnung des CAS unter Interactive  Calculation
Calculation 
 :
:
![\(A = \displaystyle \int_{-3,5}^{3,5} p(x)\; \mathrm dx = 14 \;[\text{m}^2]\)](https://www.schullv.de/resources/formulas/1f2fb92a2883d119652f3ff522ba5ca3bd0cd8fbeb74548aa40ee0fe38e210f2_light.svg)
_2015_a2_l1b2_casio.png) Damit folgt für das gesamte Volumen des Gewächshauses:
Damit folgt für das gesamte Volumen des Gewächshauses:





![\( = 168 \;[\text{m}^3]\)](https://www.schullv.de/resources/formulas/9145f6518a2705086ca8c13d0db6df3b2ff7fbc7278e513100f6102c68eacc9c_light.svg)
_2015_a2_l1b2_casio.png)
2.2
1. Schritt: Fläche des Zwischenbodens berechnen
Die Fläche des Zwischenbodens hat die Form eines Rechtecks. Die Breite ergibt sich durch den  -Wert der in Material 2 dargestellten Schnittstelle der Geraden
-Wert der in Material 2 dargestellten Schnittstelle der Geraden  mit der Parabel. Mit Hilfe des solve-Befehls des CAS folgt für die Schnittstelle:
mit der Parabel. Mit Hilfe des solve-Befehls des CAS folgt für die Schnittstelle:

_2015_a2_l1b3_casio.png) Da der Zwischenboden in der Skizze rechts von der
Da der Zwischenboden in der Skizze rechts von der  -Achse liegt, ist
-Achse liegt, ist  die gesuchte
die gesuchte  -Koordinate. Für die Breite folgt:
-Koordinate. Für die Breite folgt:



![\( \approx 2,86 \;[\text{m}]\)](https://www.schullv.de/resources/formulas/f2e7c379bccc3c306903229b4710e7d518eb69c57fc9e77ecb7433e7dbeb2219_light.svg) .
Für den Flächeninhalt des Zwischenbodens folgt damit insgesamt:
.
Für den Flächeninhalt des Zwischenbodens folgt damit insgesamt:






![\( \approx 34,3 \;[\text{m}^2].\)](https://www.schullv.de/resources/formulas/f3f2f5b9f9d32620675542c491fb0e4fd9fc9b208a6052ed906bcdb2ba409422_light.svg) 2. Schritt: Flächeninhalt der Bodenfläche der Gewächshaushälfte berechnen
Mit einer Länge von
2. Schritt: Flächeninhalt der Bodenfläche der Gewächshaushälfte berechnen
Mit einer Länge von  und einer Breite von
und einer Breite von  folgt für den Flächeninhalt der Bodenflächenhälfte:
folgt für den Flächeninhalt der Bodenflächenhälfte:



 3. Schritt: Prozentuale Abweichung berechnen
3. Schritt: Prozentuale Abweichung berechnen


 Der Zwischenbodenflächeninhalt misst damit ca.
Der Zwischenbodenflächeninhalt misst damit ca.  der Bodenfläche der Gewächshaushälfte. Somit ist der Zwischenboden etwa
der Bodenfläche der Gewächshaushälfte. Somit ist der Zwischenboden etwa  kleiner.
kleiner.
_2015_a2_l1b3_casio.png)
3.
Einsetzen von  in die Formel aus der Aufgabenstellung zur Berechnung von
in die Formel aus der Aufgabenstellung zur Berechnung von  ergibt mit
ergibt mit  und
und  Das Integral ist somit also die Länge des Graphen zwischen dem Hochpunkt und der positiven Nullstelle von
Das Integral ist somit also die Länge des Graphen zwischen dem Hochpunkt und der positiven Nullstelle von  Die
Die  in dem Term entspricht der Länge des Gewächshauses, das heißt durch Multiplikation ergibt sich die Fläche der rechten Hälfte Gewächshausdaches. Multiplikation mit
in dem Term entspricht der Länge des Gewächshauses, das heißt durch Multiplikation ergibt sich die Fläche der rechten Hälfte Gewächshausdaches. Multiplikation mit  liefert die Fläche des gesamten Daches. Der Term becshreibt also die Fläche des Gewächshausdaches.
liefert die Fläche des gesamten Daches. Der Term becshreibt also die Fläche des Gewächshausdaches.
4.1
Funktion  bestimmen
Bei der allgemeinen Gleichung
bestimmen
Bei der allgemeinen Gleichung 

 einer Funktion für den oberen Ellipsenbogen entspricht
einer Funktion für den oberen Ellipsenbogen entspricht  der Höhe des Gewächshauses und
der Höhe des Gewächshauses und  der Breite. Einsetzen von
der Breite. Einsetzen von  und
und  liefert:
liefert:






 Funktion
Funktion  skizzieren
Mit Hilfe der Wertetabelle der Funktion
skizzieren
Mit Hilfe der Wertetabelle der Funktion  die sich im CAS anzeigen lässt, folgt:
die sich im CAS anzeigen lässt, folgt:


4.2
Für die Gleichung von  folgt bei gleichbleibender Breite:
folgt bei gleichbleibender Breite:






 1. Schritt: Größe der neuen Fläche
Berechnung des Termes aus Aufgabe 3 für die alte Fläche und Multiplikation mit
1. Schritt: Größe der neuen Fläche
Berechnung des Termes aus Aufgabe 3 für die alte Fläche und Multiplikation mit  liefert für die Größe der neuen Fläche:
liefert für die Größe der neuen Fläche:






![\( \cdot 115,41 \approx 121,18 \;[\text{m}^2]\)](https://www.schullv.de/resources/formulas/8badf13f55389b23168d95b571ab42588fac77374a847ffe4f77cc75fa9af703_light.svg)
_2015_a2_l1b5_casio.png) 2. Schritt: Neue Höhe bestimmen
Definition der ersten Ableitung
2. Schritt: Neue Höhe bestimmen
Definition der ersten Ableitung  im CAS und Lösen der Gleichung
im CAS und Lösen der Gleichung  mit dem solve-Befehl des CAS liefert für die neue Höhe den Wert
mit dem solve-Befehl des CAS liefert für die neue Höhe den Wert 
Insgesamt beträgt damit die Höhendifferenz![\(3\;\text{m}-2,9\;\text{m}=0,1\;[\text{m}].\)](https://www.schullv.de/resources/formulas/69e82c6efc322f43e93af8409f84924f5cdb6ecb616528696f39d24b661c601f_light.svg)
_2015_a2_l1b5_casio.png)
Insgesamt beträgt damit die Höhendifferenz