A1 - Analysis
1
Gegeben sind die Funktionen  mit
mit  mit
mit  .
.
Im Folgenden werden die jährlichen Verkaufszahlen von Smartphones in einem Land mit 80 Millionen Einwohnern in den Jahren 2008 bis 2013 betrachtet. Hierzu wird das Jahr 2008 als Startzeitpunkt
1.1
Beschreibe den Einfluss des Parameters  auf die Kurvenverläufe.
auf die Kurvenverläufe.
(5 BE)
1.2
Bestimme die Hochpunkte und Wendepunkte der Graphen von  in Abhängigkeit von
in Abhängigkeit von  und begründe anhand der entsprechenden Ableitungsterme, dass alle Graphen jeweils nur einen Hochpunkt und einen Wendepunkt besitzen.
Hinweis: Für die Bestimmung der Wendepunkte ist die Überprüfung der notwendigen Bedingung ausreichend.
und begründe anhand der entsprechenden Ableitungsterme, dass alle Graphen jeweils nur einen Hochpunkt und einen Wendepunkt besitzen.
Hinweis: Für die Bestimmung der Wendepunkte ist die Überprüfung der notwendigen Bedingung ausreichend.
(7 BE)
1.3
In einem Fachgeschäft wird eine Werbeaktion für ein spezielles Smartphone durchgeführt. Die täglichen Verkaufszahlen lassen sich näherungsweise durch die Funktion  mit
mit  beschreiben. Hierbei steht
beschreiben. Hierbei steht  für die Zeit in Tagen nach Beginn der Werbeaktion und
für die Zeit in Tagen nach Beginn der Werbeaktion und  für die Anzahl der verkauften Smartphones pro Tag.
Bestimme den Zeitpunkt, an dem die meisten Smartphones (pro Tag) verkauft werden, sowie die ungefähre Anzahl der verkauften Geräte an diesem Tag.
Erläutere die Bedeutung der Wendestelle von
für die Anzahl der verkauften Smartphones pro Tag.
Bestimme den Zeitpunkt, an dem die meisten Smartphones (pro Tag) verkauft werden, sowie die ungefähre Anzahl der verkauften Geräte an diesem Tag.
Erläutere die Bedeutung der Wendestelle von  im Sachzusammenhang.
im Sachzusammenhang.
(4 BE)
2
Die Entwicklung der Verkaufszahlen von Smartphones in den Jahren 2008 bis 2013 wird in der folgenden Tabelle angegeben:
| Jahr | Verkaufszahlen in Millionen Stück pro Jahr | |
|---|---|---|
2.1
Zeige, dass die Entwicklung der Verkaufszahlen von Smartphones in diesem Zeitraum annähernd exponentiell verlief.
(2 BE)
2.2
Ermittle durch Regression die Funktionsgleichung einer Exponentialfunktion  der Form
der Form  , welche die Verkaufszahlen von Smartphones modelliert
, welche die Verkaufszahlen von Smartphones modelliert  Zeit in Jahren nach 2008,
Zeit in Jahren nach 2008,  Anzahl verkaufter Smartphones in Millionen Stück pro Jahr
Anzahl verkaufter Smartphones in Millionen Stück pro Jahr
(3 BE)
3.
Im Folgenden wird die Entwicklung der jährlichen Verkaufszahlen der Smartphones durch die Funktion  mit
mit  modelliert (
modelliert ( : Zeit in Jahren nach 2008,
: Zeit in Jahren nach 2008,  : Anzahl verkaufter Smartphones in Millionen Stück pro Jahr).
: Anzahl verkaufter Smartphones in Millionen Stück pro Jahr).
3.1
Skizziere den Verlauf des Funktionsgraphen von  im Intervall
im Intervall ![\([-0,5;\;5,5]\)](https://www.schullv.de/resources/formulas/d8d8f98a5caddad00365d0ef4e1e1a51f3561ab34c1cbd965c6f153b64f9a495_light.svg) in das folgende Säulendiagramm.
in das folgende Säulendiagramm.
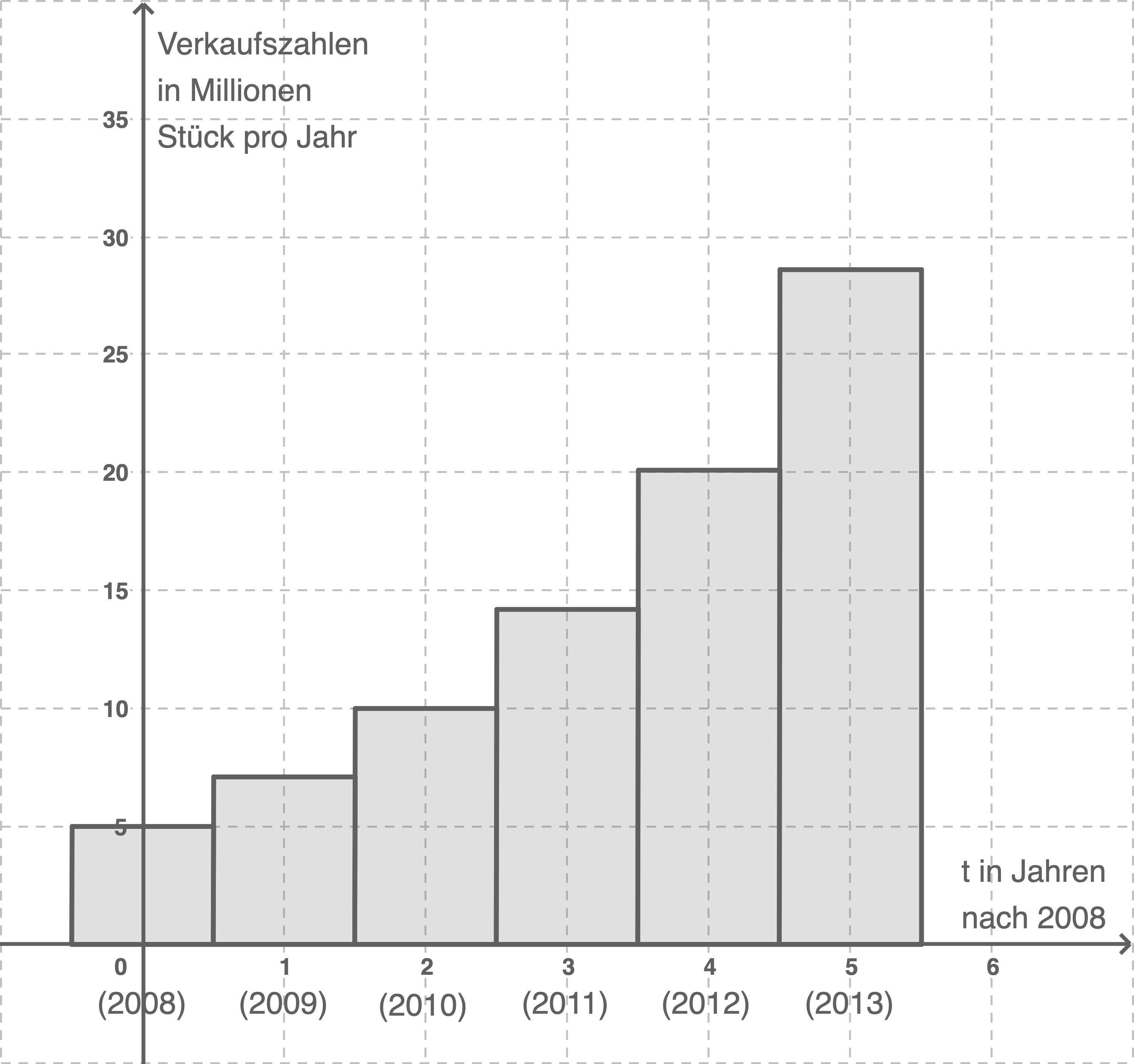

(3 BE)
3.2
Bestimme den Inhalt der Fläche, die der Graph von  mit der
mit der  -Achse im Intervall
-Achse im Intervall ![\([0;\;5]\)](https://www.schullv.de/resources/formulas/5bd4ad8253be773dc9e60f4b7442dbb4a65ba7b1e68fbe3d589c3451276e83e0_light.svg) einschließt, und deute den Wert im Sachzusammenhang.
einschließt, und deute den Wert im Sachzusammenhang.
(4 BE)
3.3
Bestimme unter Verwendung der Tabelle aus Aufgabe 2 die Gesamtzahl der in den Jahren 2008 bis einschließlich 2013 tatsächlich verkauften Smartphones.
Vergleiche diesen Wert mit dem Ergebnis aus Aufgabenteil 3.2 und erkläre die Abweichung.
Erläutere, wie durch Modifikation des Integrals aus Aufgabenteil 3.2 ein besseres Ergebnis erzielt werden kann, und gib eine Modifikation an.
(7 BE)
3.4
Bestimme mithilfe der Modellierungsfunktion  die zu erwartenden Verkaufszahlen von Smartphones im Jahr 2030 in diesem Land.
Beurteile diesen Wert sowie die Güte der Modellierung.
die zu erwartenden Verkaufszahlen von Smartphones im Jahr 2030 in diesem Land.
Beurteile diesen Wert sowie die Güte der Modellierung.
(5 BE)
1.1
Durch Einsetzen verschiedener Werte für  in die Funktion
in die Funktion  und Vergleichen der sich ergebenden Graphen kann der Einfluss des Parameters
und Vergleichen der sich ergebenden Graphen kann der Einfluss des Parameters  auf den Kurvenverlauf untersucht werden:
Hierfür muss die Funktionenschar im CAS definiert werden:
auf den Kurvenverlauf untersucht werden:
Hierfür muss die Funktionenschar im CAS definiert werden:
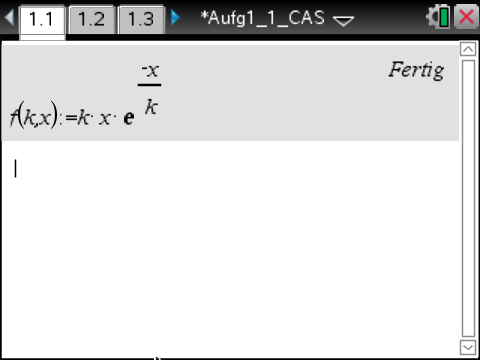 Nun können die Graphen einiger Funktionen mit verschiedenen Werten für
Nun können die Graphen einiger Funktionen mit verschiedenen Werten für  auf dem CAS angezeigt werden:
auf dem CAS angezeigt werden:
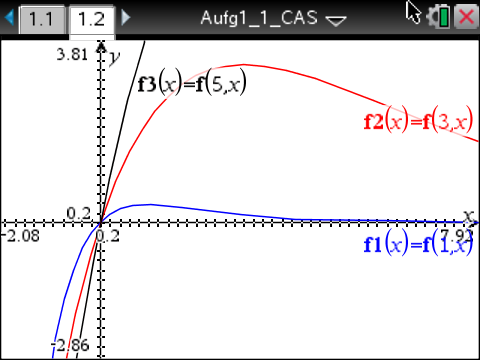 Umso größer
Umso größer  desto langsamer nähert sich der Graph asymptotisch der
desto langsamer nähert sich der Graph asymptotisch der  -Achse an. Mit größerem
-Achse an. Mit größerem  werden zudem die Werte der Koordinaten des Hochpunkts größer, sodass der Graph zunehmend höher und steiler verläuft.
werden zudem die Werte der Koordinaten des Hochpunkts größer, sodass der Graph zunehmend höher und steiler verläuft.


1.2
Hochpunkte bestimmen
1. Schritt: Ableitungen bilden
Mit dem CAS kann die erste und zweite Ableitung bestimmt werden:
Es folgt:

 2. Schritt: Notwendige Bedingung für Extremstellen anwenden
Es soll gelten:
2. Schritt: Notwendige Bedingung für Extremstellen anwenden
Es soll gelten:
![\(\begin{array}[t]{rll}
f_k](https://www.schullv.de/resources/formulas/8ba3513bed559178fca87f5d3b8df604e6ef8bd6984344b9543443df48db8b9f_light.svg) Mit dem solve-Befehl ergibt sich
Mit dem solve-Befehl ergibt sich  3. Schritt: Hinreichende Bedingung für Extremstellen anwenden
3. Schritt: Hinreichende Bedingung für Extremstellen anwenden
![\(\begin{array}[t]{rll}
f_k](https://www.schullv.de/resources/formulas/25f5684282295f9ac165793d4f03b97557d586d2d6dc69895f5becb097ee3737_light.svg) Da
Da  ist, handelt es sich bei
ist, handelt es sich bei  folglich um eine Maximalstelle.
4. Schritt:
folglich um eine Maximalstelle.
4. Schritt:  -Koordinate bestimmen
Mit dem CAS ergibt sich:
-Koordinate bestimmen
Mit dem CAS ergibt sich:
 Die Graphen von
Die Graphen von  besitzen also einen Hochpunkt mit den Koordinaten
besitzen also einen Hochpunkt mit den Koordinaten  .
Wendepunkte bestimmen
1. Schritt: Notwendige Bedingung für Wendestellen anwenden
Es soll gelten:
.
Wendepunkte bestimmen
1. Schritt: Notwendige Bedingung für Wendestellen anwenden
Es soll gelten:
![\(\begin{array}[t]{rll}
f_k](https://www.schullv.de/resources/formulas/e62192ca412363fe641223af2cd7ff8e3a760e649527e0a3369047ae1102eb51_light.svg) Mit dem solve-Befehl des CAS folgt
Mit dem solve-Befehl des CAS folgt  Laut Aufgabenstellung ist die Untersuchung der notwendigen Bedingung ausreichend. Die hinreichende Bedingung muss somit nicht mehr geprüft werden.
2. Schritt:
Laut Aufgabenstellung ist die Untersuchung der notwendigen Bedingung ausreichend. Die hinreichende Bedingung muss somit nicht mehr geprüft werden.
2. Schritt:  -Koordinate bestimmen
Mit dem CAS ergibt sich für
-Koordinate bestimmen
Mit dem CAS ergibt sich für 
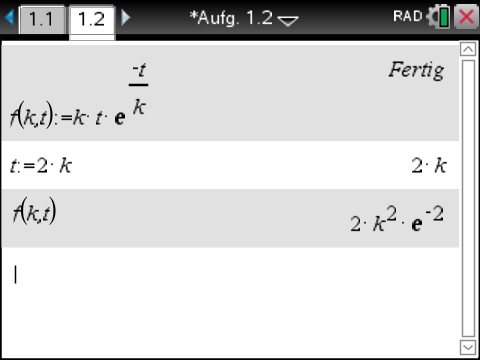 Die Koordinaten des Wendepunkts
Die Koordinaten des Wendepunkts  der Graphen von
der Graphen von  folgen also mit
folgen also mit  .
Begründung
Die notwendige Bedingung für einen Wendepunkt ist gegeben durch:
.
Begründung
Die notwendige Bedingung für einen Wendepunkt ist gegeben durch:
![\(\begin{array}[t]{rll}
f_k](https://www.schullv.de/resources/formulas/98d46e04365d5411e681f7c0d3867c65372b4d1aefd45c936dba4ff41b6eebae_light.svg) Mit dem Satz vom Nullprodukt folgt
Mit dem Satz vom Nullprodukt folgt  für alle
für alle  und somit ist die einzige Lösung des Terms gegeben durch
und somit ist die einzige Lösung des Terms gegeben durch  Da unabhängig von
Da unabhängig von  in allen Fällen nur ein Wert von
in allen Fällen nur ein Wert von  die Gleichung löst, nämlich genau
die Gleichung löst, nämlich genau  erfüllt nur ein Wert von
erfüllt nur ein Wert von  die notwendige Bedingung für Extremstellen. Alle Graphen haben somit genau einen Hochpunkt.
Analog lautet die Begründung für die Existenz genau eines Wendepunkts:
Zum Prüfen der notwendigen Bedingung für einen Wendepunkt muss die zweite Ableitung
die notwendige Bedingung für Extremstellen. Alle Graphen haben somit genau einen Hochpunkt.
Analog lautet die Begründung für die Existenz genau eines Wendepunkts:
Zum Prüfen der notwendigen Bedingung für einen Wendepunkt muss die zweite Ableitung  gleich Null gesetzt werden. Mit dem Satz vom Nullpunkt kann die Gleichung nun gelöst werden.
Da der Faktor
gleich Null gesetzt werden. Mit dem Satz vom Nullpunkt kann die Gleichung nun gelöst werden.
Da der Faktor  mit
mit  für jedes
für jedes  größer Null ist, kann nur noch der Faktor
größer Null ist, kann nur noch der Faktor  Null werden. Da die notwendige Bedingung für eine Wendestelle somit nur für einen Wert von
Null werden. Da die notwendige Bedingung für eine Wendestelle somit nur für einen Wert von  erfüllt wird, besitzen die Graphen von
erfüllt wird, besitzen die Graphen von  foglich genau einen Wendepunkt.
foglich genau einen Wendepunkt.
menu  4: Analysis
4: Analysis  1: Ableitung
1: Ableitung


1.3
Zeitpunkt bestimmen
Der Zeitpunkt, an dem die meisten Smartphones pro Tag verkauft werden, entspricht der Maximalstelle der Funktion  .
Im Aufgabenteil 1.2 wurde bereits der Hochpunkt der Funktion
.
Im Aufgabenteil 1.2 wurde bereits der Hochpunkt der Funktion  in Abhängigkeit des Parameters
in Abhängigkeit des Parameters  bestimmt:
bestimmt:
 Für
Für  folgen die Koordinaten des Hochpunkts also mit
folgen die Koordinaten des Hochpunkts also mit  Die meisten Smartphones werden also am 15. Tag nach Beginn der Werbeaktion verkauft.
Anzahl der verkauften Smartphones berechnen
Die Anzahl der verkauften Smartphones am 15. Tag nach Beginn der Werbeaktion entspricht dem Funktionswert von
Die meisten Smartphones werden also am 15. Tag nach Beginn der Werbeaktion verkauft.
Anzahl der verkauften Smartphones berechnen
Die Anzahl der verkauften Smartphones am 15. Tag nach Beginn der Werbeaktion entspricht dem Funktionswert von  an der Stelle
an der Stelle  Die
Die  -Koordinate des Hochpunkts ist bereits gegeben durch:
-Koordinate des Hochpunkts ist bereits gegeben durch:
 Am 15. Tag werden somit ungefähr 83 Smartphones verkauft.
Bedeutung der Wendestelle erläutern
Die Wendestelle von
Am 15. Tag werden somit ungefähr 83 Smartphones verkauft.
Bedeutung der Wendestelle erläutern
Die Wendestelle von  beschreibt den Zeitpunkt, an dem die Verkaufszahlen am stärksten zu- beziehungsweise abnehmen.
Einsetzen von
beschreibt den Zeitpunkt, an dem die Verkaufszahlen am stärksten zu- beziehungsweise abnehmen.
Einsetzen von  in die Koordinaten des Wendepunkts aus Aufgabenteil 1.2 ergibt
in die Koordinaten des Wendepunkts aus Aufgabenteil 1.2 ergibt  In Zusammenhang mit dem Verlauf des entsprechenden Graphen folgt somit, dass die Verkaufszahlen am 30. Tag nach Beginn der Werbeaktion am stärksten abnehmen.
In Zusammenhang mit dem Verlauf des entsprechenden Graphen folgt somit, dass die Verkaufszahlen am 30. Tag nach Beginn der Werbeaktion am stärksten abnehmen.
2.1
Bei einem exponentiellen Wachstum erhöht sich der Funktionswert pro Zeitschritt immer um den gleichen Faktor:




 Da sich ein annähernd konstanter Wachstumsfaktor erkennen lässt, handelt es sich hierbei um ein exponentielles Wachstum mit einem Mittelwert von 1,42.
Da sich ein annähernd konstanter Wachstumsfaktor erkennen lässt, handelt es sich hierbei um ein exponentielles Wachstum mit einem Mittelwert von 1,42.
2.2
1. Schritt: Werte aus der Tabelle in das 4:Lists&Spreadsheet-Menu eingeben
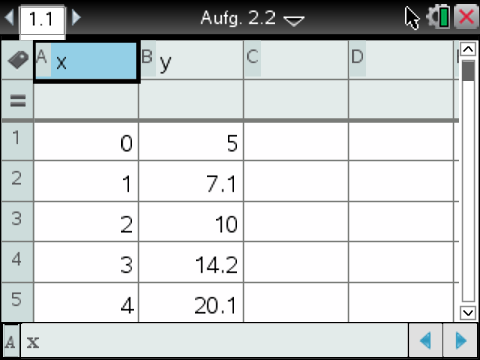 2. Schritt: Exponentielle Regression durchführen
Durch Auswahl von 4:Statistik aus dem 4. Reiter des Menu kann eine exponentielle Regression ausgeführt werden.
Hierzu wird die X-Liste als a[] und die Y-Liste als b[] benannt.
2. Schritt: Exponentielle Regression durchführen
Durch Auswahl von 4:Statistik aus dem 4. Reiter des Menu kann eine exponentielle Regression ausgeführt werden.
Hierzu wird die X-Liste als a[] und die Y-Liste als b[] benannt.
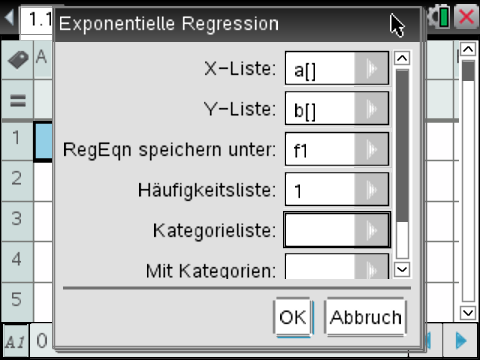 Nach der Bestätigung der Auswahl mit OK können die Werte für die Parameter
Nach der Bestätigung der Auswahl mit OK können die Werte für die Parameter  und
und  aus der Tabelle abgelesen werden:
aus der Tabelle abgelesen werden:
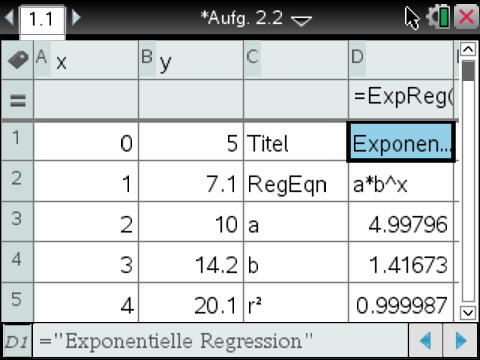 Es ergeben sich also folgende Werte:
Es ergeben sich also folgende Werte:

 Die gesuchte Gleichung lautet also:
Die gesuchte Gleichung lautet also:




3.1
Mit dem CAS kann eine Wertetabelle zur Funktion  erstellt werden:
Die Werte von
erstellt werden:
Die Werte von  können im CAS im 4:Lists&Spreadsheet-Menu unter A eingefügt werden.
Die Funktionsvorschrift
können im CAS im 4:Lists&Spreadsheet-Menu unter A eingefügt werden.
Die Funktionsvorschrift  kann anschließend unter B eingefügt werden.
Der CAS berechnet nun die jeweiligen
kann anschließend unter B eingefügt werden.
Der CAS berechnet nun die jeweiligen  -Werte für
-Werte für 
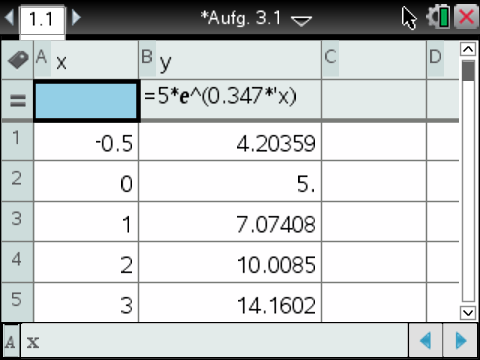 Durch Eintragen der gegebenen Punkte aus der Wertetabelle in das Säulendiagramm und Verbinden der benachbarten Punkte kann nun der Verlauf des Funktionsgraphen skizziert werden:
Durch Eintragen der gegebenen Punkte aus der Wertetabelle in das Säulendiagramm und Verbinden der benachbarten Punkte kann nun der Verlauf des Funktionsgraphen skizziert werden:
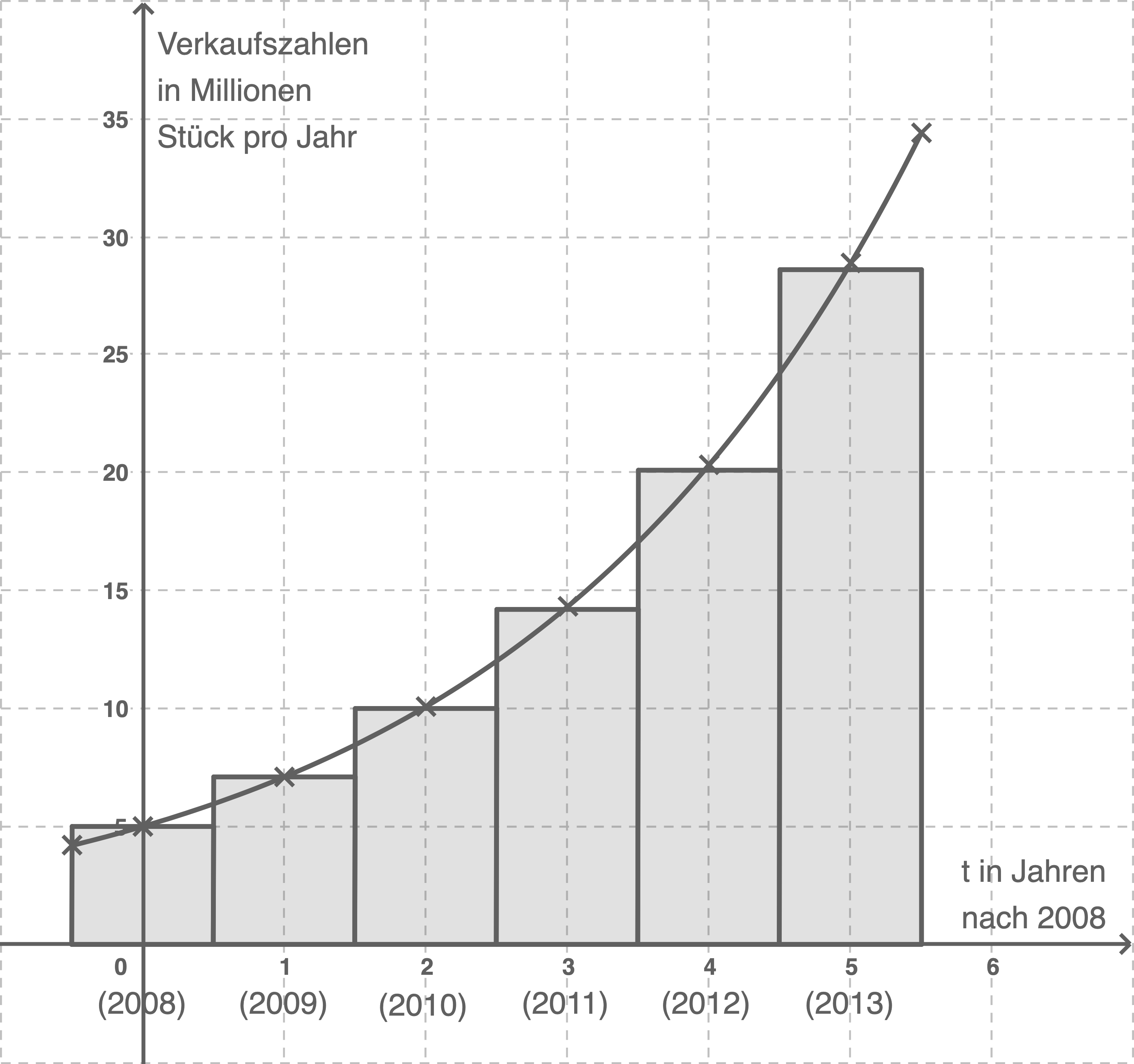


3.2
Inhalt der Fläche bestimmen
Der Funktionsterm von  kann im CAS gespeichert werden und anschließend kann unter 4:Analysis der 2. Reiter Numerisches Integral gewählt werden.
Die Integrationsgrenzen sind gegeben durch
kann im CAS gespeichert werden und anschließend kann unter 4:Analysis der 2. Reiter Numerisches Integral gewählt werden.
Die Integrationsgrenzen sind gegeben durch ![\([0;5].\)](https://www.schullv.de/resources/formulas/659ef5483ce5cb640d326dd5b366008ecca85ad92da628bbb9b16df35227ba5a_light.svg)
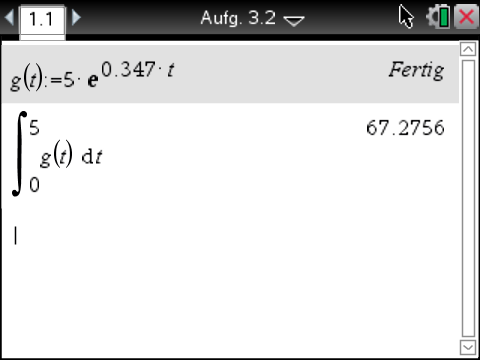 Es ergibt sich:
Es ergibt sich:
![\(\begin{array}[t]{rll}
\displaystyle\int_{0}^{5}g(t)\;\mathrm dt \approx 67,28 \; [ \; \text{Mio.}]\quad \scriptsize \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/455b8918640194cace0a9a2ddcfe434765d26a839f47760bf7cfbabe2f9b864a_light.svg) Wert im Sachzusammenhang deuten
Das Integral beschreibt den Flächeninhalt unter dem Graphen zwischen
Wert im Sachzusammenhang deuten
Das Integral beschreibt den Flächeninhalt unter dem Graphen zwischen  und
und  Dieser Flächeninhalt entspricht der Anzahl aller zwischen Mitte 2008 und Mitte 2013 verkauften Smartphones.
Zwischen Mitte 2008 und Mitte 2013 wurden somit etwa 67,28 Millionen Smartphones verkauft.
Dieser Flächeninhalt entspricht der Anzahl aller zwischen Mitte 2008 und Mitte 2013 verkauften Smartphones.
Zwischen Mitte 2008 und Mitte 2013 wurden somit etwa 67,28 Millionen Smartphones verkauft.

3.3
Gesamtzahl bestimmen
Aufsummieren der Verkaufszahlen der Jahre 2008 bis 2013 aus der Tabelle ergibt:
Zwischen 2008 und 2013 wurden folglich 85 Millionen Smartphones verkauft.
Abweichung erklären
In Aufgabenteil 3.2 ergab sich die gesamte Verkaufszahl mit Hilfe das Integrals durch etwa 67,28 Millionen Smartphones.
Im Säulendiagramms kann abgelesen werden, dass der Zeitpunkt  nicht mit dem Anfang des Jahres 2008 übereinstimmt, sondern in der Mitte der entsprechenden Säule liegt.
In der Berechnung mit dem Integral fehlt folglich das erste Halbjahr von 2008. Analog verhält es sich mit dem zweiten Halbjahr von 2013. Somit fehlt jeweils die Hälfte der Verkaufszahlen von 2008 und 2013.
Der mit dem Integral berechnete Wert ist deshalb deutlich kleiner als der tatsächliche Wert der Verkaufszahl.
Modifikation erläutern
Um den gesamten Zeitraum von Anfang 2008 bis Ende 2013 im Integral zu berücksichtigen, müssen die Grenzen des Integrals verändert werden. Das Jahr 2008 beginnt zum Zeitpunkt
nicht mit dem Anfang des Jahres 2008 übereinstimmt, sondern in der Mitte der entsprechenden Säule liegt.
In der Berechnung mit dem Integral fehlt folglich das erste Halbjahr von 2008. Analog verhält es sich mit dem zweiten Halbjahr von 2013. Somit fehlt jeweils die Hälfte der Verkaufszahlen von 2008 und 2013.
Der mit dem Integral berechnete Wert ist deshalb deutlich kleiner als der tatsächliche Wert der Verkaufszahl.
Modifikation erläutern
Um den gesamten Zeitraum von Anfang 2008 bis Ende 2013 im Integral zu berücksichtigen, müssen die Grenzen des Integrals verändert werden. Das Jahr 2008 beginnt zum Zeitpunkt  und das Jahr 2013 endet zum Zeitpunkt
und das Jahr 2013 endet zum Zeitpunkt  .
Die untere Grenze des Integrals soll also nun
.
Die untere Grenze des Integrals soll also nun  sein, die obere Grenze
sein, die obere Grenze  .
Modifikation angeben
Das modifizierte Integral lautet:
.
Modifikation angeben
Das modifizierte Integral lautet: 
3.4
Verkaufszahlen bestimmen
Für das Jahr 2030 gilt:
![\(\begin{array}[t]{rll}
2008& \mathrel{\widehat{=}}&t = 0 & \\[5pt]
2030& \mathrel{\widehat{=}}&t = 22
\end{array}\)](https://www.schullv.de/resources/formulas/1eebbaee9feac19d05fa7d397ac46ed0d0aece39cc0a4dd61201447669d23da1_light.svg) Einsetzen von
Einsetzen von  in die Funktionsgleichug von
in die Funktionsgleichug von  ergibt:
ergibt:
![\(\begin{array}[t]{rll}
g(22)&=& 5 \cdot \mathrm e^{0,347 \cdot 22}&; \\[5pt]
&\approx& 10336,5 \; \text{[Mio.]}
\end{array}\)](https://www.schullv.de/resources/formulas/adb9ff07fe02595201471ea28e930bd3229e13a50b89032d5a7df3cd1f00d19f_light.svg) Die zu erwartende Verkaufszahl von Smartphones im Jahr 2030 entspricht etwa 10336,5 Millionen, also mehr als 10 Milliarden Smartphones.
Modellierung bewerten
Die errechnete Verkaufszahl für 2030 von über 10 Milliarden Smartphones ist nicht plausibel, da ein Land von 80 Millionen Einwohnern betrachtet wird. Es ist sehr unwahrscheinlich, dass 80 Millionen Menschen im Jahr 2030 10 Milliarden Smartphones kaufen.
Zudem erfährt der Markt eine zunehmende Sättigung, wodurch die Nachfrage nach einem Produkt sinkt. Ein dauerhaft exponentielles Wachstum der Verkaufszahlen ist also nicht realistisch.
Die zu erwartende Verkaufszahl von Smartphones im Jahr 2030 entspricht etwa 10336,5 Millionen, also mehr als 10 Milliarden Smartphones.
Modellierung bewerten
Die errechnete Verkaufszahl für 2030 von über 10 Milliarden Smartphones ist nicht plausibel, da ein Land von 80 Millionen Einwohnern betrachtet wird. Es ist sehr unwahrscheinlich, dass 80 Millionen Menschen im Jahr 2030 10 Milliarden Smartphones kaufen.
Zudem erfährt der Markt eine zunehmende Sättigung, wodurch die Nachfrage nach einem Produkt sinkt. Ein dauerhaft exponentielles Wachstum der Verkaufszahlen ist also nicht realistisch.
1.1
Durch Einsetzen verschiedener Werte für  in die Funktion
in die Funktion  und Vergleichen der sich ergebenden Graphen kann der Einfluss des Parameters
und Vergleichen der sich ergebenden Graphen kann der Einfluss des Parameters  auf den Kurvenverlauf untersucht werden:
auf den Kurvenverlauf untersucht werden:
 Umso größer
Umso größer  desto langsamer nähert sich der Graph asymptotisch der
desto langsamer nähert sich der Graph asymptotisch der  -Achse an. Mit größerem
-Achse an. Mit größerem  werden zudem die Werte der Koordinaten des Hochpunkts größer, sodass der Graph zunehmend höher und steiler verläuft.
werden zudem die Werte der Koordinaten des Hochpunkts größer, sodass der Graph zunehmend höher und steiler verläuft.

1.2
Hochpunkte bestimmen
1. Schritt: Notwendige Bedingung für Extremstellen anwenden
Mit dem CAS können der Funktionsterm von  und die erste Ableitung
und die erste Ableitung  definiert werden.
Es soll gelten:
definiert werden.
Es soll gelten:  Mit dem solve-befehl folgt:
Mit dem solve-befehl folgt:
 Als mögliche Extremstelle ergibt sich somit
Als mögliche Extremstelle ergibt sich somit  2. Schritt: Hinreichende Bedingung für Extremstellen anwenden
Nach dem Definieren der zweiten Ableitung
2. Schritt: Hinreichende Bedingung für Extremstellen anwenden
Nach dem Definieren der zweiten Ableitung  im CAS kann der Wert von
im CAS kann der Wert von  berechnet werden:
berechnet werden:
 Es ergibt sich also:
Es ergibt sich also:
 Bei
Bei  handelt es sich folglich um eine Maximalstelle.
3. Schritt:
handelt es sich folglich um eine Maximalstelle.
3. Schritt:  -Koordinate bestimmen Mit dem CAS ergibt sich:
-Koordinate bestimmen Mit dem CAS ergibt sich:
 Die Graphen von
Die Graphen von  besitzen also einen Hochpunkt mit den Koordinaten
besitzen also einen Hochpunkt mit den Koordinaten  .
Wendepunkte bestimmen
1. Schritt: Notwendige Bedingung für Wendestellen anwenden
Die zweite Ableitung
.
Wendepunkte bestimmen
1. Schritt: Notwendige Bedingung für Wendestellen anwenden
Die zweite Ableitung  ist bereits im definiert.
Es soll gelten:
ist bereits im definiert.
Es soll gelten:  Mit dem solve-Befehl des CAS folgt:
Mit dem solve-Befehl des CAS folgt:
 Laut Aufgabenstellung ist die Untersuchung der notwendigen Bedingung ausreichend. Die hinreichende Bedingung muss somit nicht mehr geprüft werden.
Die Wendestelle ergibt sich also an der Stelle
Laut Aufgabenstellung ist die Untersuchung der notwendigen Bedingung ausreichend. Die hinreichende Bedingung muss somit nicht mehr geprüft werden.
Die Wendestelle ergibt sich also an der Stelle  2. Schritt:
2. Schritt:  -Koordinate bestimmen
Mit dem CAS ergibt sich für
-Koordinate bestimmen
Mit dem CAS ergibt sich für 
 Die Koordinaten des Wendepunkts
Die Koordinaten des Wendepunkts  der Graphen von
der Graphen von  folgen also mit
folgen also mit  .
Begründung
Die notwendige Bedingung für einen Wendepunkt ist gegeben durch:
.
Begründung
Die notwendige Bedingung für einen Wendepunkt ist gegeben durch:
![\(\begin{array}[t]{rll}
f_k](https://www.schullv.de/resources/formulas/98d46e04365d5411e681f7c0d3867c65372b4d1aefd45c936dba4ff41b6eebae_light.svg) Mit dem Satz vom Nullprodukt folgt
Mit dem Satz vom Nullprodukt folgt  für alle
für alle  und somit ist die einzige Lösung des Terms gegeben durch
und somit ist die einzige Lösung des Terms gegeben durch  Da unabhängig von
Da unabhängig von  in allen Fällen nur ein Wert von
in allen Fällen nur ein Wert von  die Gleichung löst, nämlich genau
die Gleichung löst, nämlich genau  erfüllt nur ein Wert von
erfüllt nur ein Wert von  die notwendige Bedingung für Extremstellen. Alle Graphen haben somit genau einen Hochpunkt.
Analog lautet die Begründung für die Existenz genau eines Wendepunkts:
Zum Prüfen der notwendigen Bedingung für einen Wendepunkt muss die zweite Ableitung
die notwendige Bedingung für Extremstellen. Alle Graphen haben somit genau einen Hochpunkt.
Analog lautet die Begründung für die Existenz genau eines Wendepunkts:
Zum Prüfen der notwendigen Bedingung für einen Wendepunkt muss die zweite Ableitung  gleich Null gesetzt werden. Mit dem Satz vom Nullpunkt kann die Gleichung nun gelöst werden.
Da der Faktor
gleich Null gesetzt werden. Mit dem Satz vom Nullpunkt kann die Gleichung nun gelöst werden.
Da der Faktor  mit
mit  für jedes
für jedes  größer Null ist, kann nur noch der Faktor
größer Null ist, kann nur noch der Faktor  Null werden. Da die notwendige Bedingung für eine Wendestelle somit nur für einen Wert von
Null werden. Da die notwendige Bedingung für eine Wendestelle somit nur für einen Wert von  erfüllt wird, besitzen die Graphen von
erfüllt wird, besitzen die Graphen von  foglich genau einen Wendepunkt.
foglich genau einen Wendepunkt.





1.3
Zeitpunkt bestimmen
Der Zeitpunkt, an dem die meisten Smartphones pro Tag verkauft werden, entspricht der Maximalstelle der Funktion  .
Im Aufgabenteil 1.2 wurde bereits der Hochpunkt der Funktion
.
Im Aufgabenteil 1.2 wurde bereits der Hochpunkt der Funktion  in Abhängigkeit des Parameters
in Abhängigkeit des Parameters  bestimmt:
bestimmt:
 Für
Für  folgen die Koordinaten des Hochpunkts also mit
folgen die Koordinaten des Hochpunkts also mit  Die meisten Smartphones werden also am 15. Tag nach Beginn der Werbeaktion verkauft.
Anzahl der verkauften Smartphones berechnen
Die Anzahl der verkauften Smartphones am 15. Tag nach Beginn der Werbeaktion entspricht dem Funktionswert von
Die meisten Smartphones werden also am 15. Tag nach Beginn der Werbeaktion verkauft.
Anzahl der verkauften Smartphones berechnen
Die Anzahl der verkauften Smartphones am 15. Tag nach Beginn der Werbeaktion entspricht dem Funktionswert von  an der Stelle
an der Stelle  Die
Die  -Koordinate des Hochpunkts ist bereits gegeben durch:
-Koordinate des Hochpunkts ist bereits gegeben durch:
 Am 15. Tag werden somit ungefähr 83 Smartphones verkauft.
Bedeutung der Wendestelle erläutern
Die Wendestelle von
Am 15. Tag werden somit ungefähr 83 Smartphones verkauft.
Bedeutung der Wendestelle erläutern
Die Wendestelle von  beschreibt den Zeitpunkt, an dem die Verkaufszahlen am stärksten zu- beziehungsweise abnehmen.
Einsetzen von
beschreibt den Zeitpunkt, an dem die Verkaufszahlen am stärksten zu- beziehungsweise abnehmen.
Einsetzen von  in die Koordinaten des Wendepunkts aus Aufgabenteil 1.2 ergibt
in die Koordinaten des Wendepunkts aus Aufgabenteil 1.2 ergibt  In Zusammenhang mit dem Verlauf des entsprechenden Graphen folgt somit, dass die Verkaufszahlen am 30. Tag nach Beginn der Werbeaktion am stärksten abnehmen.
In Zusammenhang mit dem Verlauf des entsprechenden Graphen folgt somit, dass die Verkaufszahlen am 30. Tag nach Beginn der Werbeaktion am stärksten abnehmen.
2.1
Bei einem exponentiellen Wachstum erhöht sich der Funktionswert pro Zeitschritt immer um den gleichen Faktor:




 Da sich ein annähernd konstanter Wachstumsfaktor erkennen lässt, handelt es sich hierbei um ein exponentielles Wachstum mit einem Mittelwert von 1,42.
Da sich ein annähernd konstanter Wachstumsfaktor erkennen lässt, handelt es sich hierbei um ein exponentielles Wachstum mit einem Mittelwert von 1,42.
2.2
Im Tabellenkalkulat-Menu können die Werte aus der Tabelle unter A eingetragen werden.
Mit folgendem Befehl kann anschließend die Regression durchgeführt werden:
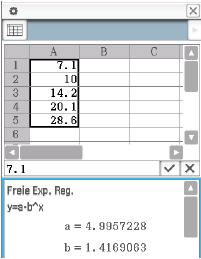 Es ergeben sich also folgende Werte:
Es ergeben sich also folgende Werte:

 Die gesuchte Gleichung lautet also:
Die gesuchte Gleichung lautet also:

Calc  Regressionen
Regressionen  Freie Exp. Regression
Freie Exp. Regression

3.1
Mit dem CAS kann im Grafik & Tabelle-Menu die Funktionsvorschrift  eingegeben werden.
In der Symbolleiste kann nun der 4. Reiter gewählt werden und der Startwert zu 0.5, das Ende zu 5.5 und die Schrittw. zu 0.5 definiert werden.
Die zugehörigen
eingegeben werden.
In der Symbolleiste kann nun der 4. Reiter gewählt werden und der Startwert zu 0.5, das Ende zu 5.5 und die Schrittw. zu 0.5 definiert werden.
Die zugehörigen  -Werte können durch Anwählen des Listensymbols im 3. Reiter bestimmt werden.
-Werte können durch Anwählen des Listensymbols im 3. Reiter bestimmt werden.
 Durch Eintragen der gegebenen Punkte aus der Wertetabelle in das Säulendiagramm und Verbinden der benachbarten Punkte kann nun der Verlauf des Funktionsgraphen skizziert werden:
Durch Eintragen der gegebenen Punkte aus der Wertetabelle in das Säulendiagramm und Verbinden der benachbarten Punkte kann nun der Verlauf des Funktionsgraphen skizziert werden:



3.2
Inhalt der Fläche bestimmen
Nach dem Definieren der Funktion  im CAS kann im Keyboard-Modus unter dem 3. Reiter Math3 das Integrationssymbol mit Integrationsgrenzen gewählt werden.
Die untere Grenze ist hierbei gegeben durch
im CAS kann im Keyboard-Modus unter dem 3. Reiter Math3 das Integrationssymbol mit Integrationsgrenzen gewählt werden.
Die untere Grenze ist hierbei gegeben durch  und die obere Grenze durch
und die obere Grenze durch  Durch EXE kann die Funktion bestätigt werden und durch den Befehl approx ergibt sich im Anschluss der gerundete Wert des Integrals.
Durch EXE kann die Funktion bestätigt werden und durch den Befehl approx ergibt sich im Anschluss der gerundete Wert des Integrals.
 Es ergibt sich:
Es ergibt sich: ![\(\begin{array}[t]{rll}
\displaystyle\int_{0}^{5}g(t)\;\mathrm dt \approx 67,28 \; [ \; \text{Mio.}]\quad \scriptsize \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/455b8918640194cace0a9a2ddcfe434765d26a839f47760bf7cfbabe2f9b864a_light.svg) Wert im Sachzusammenhang deuten
Das Integral beschreibt den Flächeninhalt unter dem Graphen zwischen
Wert im Sachzusammenhang deuten
Das Integral beschreibt den Flächeninhalt unter dem Graphen zwischen  und
und  Dieser Flächeninhalt entspricht der Anzahl aller zwischen Mitte 2008 und Mitte 2013 verkauften Smartphones.
Zwischen Mitte 2008 und Mitte 2013 wurden somit etwa 67,28 Millionen Smartphones verkauft.
Dieser Flächeninhalt entspricht der Anzahl aller zwischen Mitte 2008 und Mitte 2013 verkauften Smartphones.
Zwischen Mitte 2008 und Mitte 2013 wurden somit etwa 67,28 Millionen Smartphones verkauft.

3.3
Gesamtzahl bestimmen
Aufsummieren der Verkaufszahlen der Jahre 2008 bis 2013 aus der Tabelle ergibt:
Zwischen 2008 und 2013 wurden folglich 85 Millionen Smartphones verkauft.
Abweichung erklären
In Aufgabenteil 3.2 ergab sich die gesamte Verkaufszahl mit Hilfe das Integrals durch etwa 67,28 Millionen Smartphones.
Im Säulendiagramms kann abgelesen werden, dass der Zeitpunkt  nicht mit dem Anfang des Jahres 2008 übereinstimmt, sondern in der Mitte der entsprechenden Säule liegt.
In der Berechnung mit dem Integral fehlt folglich das erste Halbjahr von 2008. Analog verhält es sich mit dem zweiten Halbjahr von 2013. Somit fehlt jeweils die Hälfte der Verkaufszahlen von 2008 und 2013.
Der mit dem Integral berechnete Wert ist deshalb deutlich kleiner als der tatsächliche Wert der Verkaufszahl.
Modifikation erläutern
Um den gesamten Zeitraum von Anfang 2008 bis Ende 2013 im Integral zu berücksichtigen, müssen die Grenzen des Integrals verändert werden. Das Jahr 2008 beginnt zum Zeitpunkt
nicht mit dem Anfang des Jahres 2008 übereinstimmt, sondern in der Mitte der entsprechenden Säule liegt.
In der Berechnung mit dem Integral fehlt folglich das erste Halbjahr von 2008. Analog verhält es sich mit dem zweiten Halbjahr von 2013. Somit fehlt jeweils die Hälfte der Verkaufszahlen von 2008 und 2013.
Der mit dem Integral berechnete Wert ist deshalb deutlich kleiner als der tatsächliche Wert der Verkaufszahl.
Modifikation erläutern
Um den gesamten Zeitraum von Anfang 2008 bis Ende 2013 im Integral zu berücksichtigen, müssen die Grenzen des Integrals verändert werden. Das Jahr 2008 beginnt zum Zeitpunkt  und das Jahr 2013 endet zum Zeitpunkt
und das Jahr 2013 endet zum Zeitpunkt  .
Die untere Grenze des Integrals soll also nun
.
Die untere Grenze des Integrals soll also nun  sein, die obere Grenze
sein, die obere Grenze  .
Modifikation angeben
Das modifizierte Integral lautet:
.
Modifikation angeben
Das modifizierte Integral lautet: 
3.4
Verkaufszahlen bestimmen
Für das Jahr 2030 gilt:
![\(\begin{array}[t]{rll}
2008& \mathrel{\widehat{=}}&t = 0 & \\[5pt]
2030& \mathrel{\widehat{=}}&t = 22
\end{array}\)](https://www.schullv.de/resources/formulas/1eebbaee9feac19d05fa7d397ac46ed0d0aece39cc0a4dd61201447669d23da1_light.svg) Einsetzen von
Einsetzen von  in die Funktionsgleichug von
in die Funktionsgleichug von  ergibt:
ergibt:
![\(\begin{array}[t]{rll}
g(22)&=& 5 \cdot \mathrm e^{0,347 \cdot 22}&; \\[5pt]
&\approx& 10336,5 \; \text{[Mio.]}
\end{array}\)](https://www.schullv.de/resources/formulas/adb9ff07fe02595201471ea28e930bd3229e13a50b89032d5a7df3cd1f00d19f_light.svg) Die zu erwartende Verkaufszahl von Smartphones im Jahr 2030 entspricht etwa 10336,5 Millionen, also mehr als 10 Milliarden Smartphones.
Modellierung bewerten
Die errechnete Verkaufszahl für 2030 von über 10 Milliarden Smartphones ist nicht plausibel, da ein Land von 80 Millionen Einwohnern betrachtet wird. Es ist sehr unwahrscheinlich, dass 80 Millionen Menschen im Jahr 2030 10 Milliarden Smartphones kaufen.
Zudem erfährt der Markt eine zunehmende Sättigung, wodurch die Nachfrage nach einem Produkt sinkt. Ein dauerhaft exponentielles Wachstum der Verkaufszahlen ist also nicht realistisch.
Die zu erwartende Verkaufszahl von Smartphones im Jahr 2030 entspricht etwa 10336,5 Millionen, also mehr als 10 Milliarden Smartphones.
Modellierung bewerten
Die errechnete Verkaufszahl für 2030 von über 10 Milliarden Smartphones ist nicht plausibel, da ein Land von 80 Millionen Einwohnern betrachtet wird. Es ist sehr unwahrscheinlich, dass 80 Millionen Menschen im Jahr 2030 10 Milliarden Smartphones kaufen.
Zudem erfährt der Markt eine zunehmende Sättigung, wodurch die Nachfrage nach einem Produkt sinkt. Ein dauerhaft exponentielles Wachstum der Verkaufszahlen ist also nicht realistisch.