Anstiegswinkel einer Geraden
Anstiegswinkel
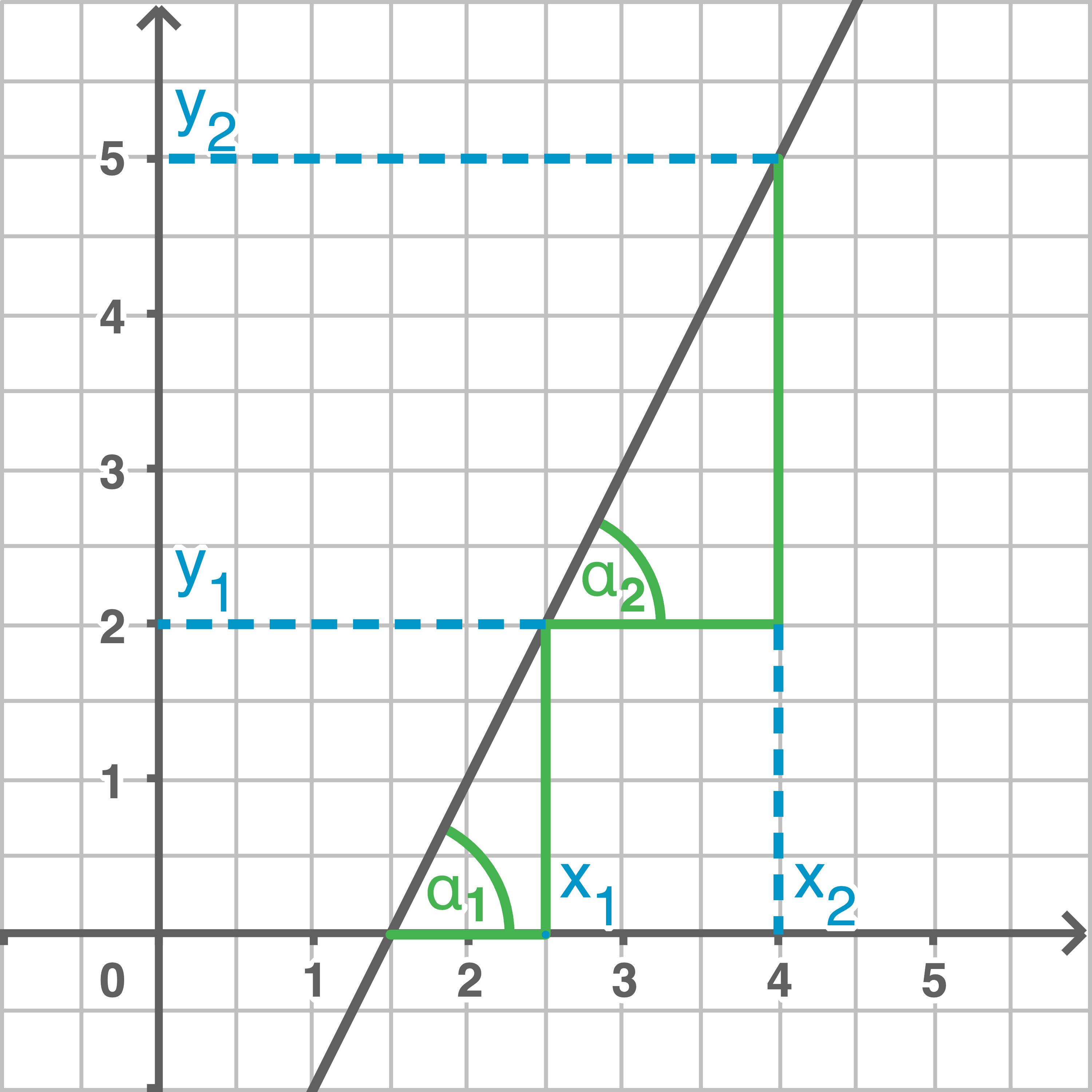
In einem rechtwinkligen Steigungsdreieck gilt:
![\(\begin{array}[t]{rll}
m&=& \dfrac{y_2-y_1}{x_2-x_1} & \\[5pt]
&=& \dfrac{\text{Gegenkathete}}{\text{Ankathete}} & \\[5pt]
&=& \tan(\alpha )
\end{array}\)](https://mathjax.schullv.de/3cb49f5d46186ebe63e61bac37cfaa63b8db6fb6104aa16fdcffcce6571f11c9?color=5a5a5a)
Der Anstieg 
einer Geraden entspricht somit dem Tangens ihres Anstiegswinkels. Für 
gilt also:
Hat eine Gerade die Gleichung 
ist also parallel zur 
-Achse, so gilt 
.
Schnittwinkel
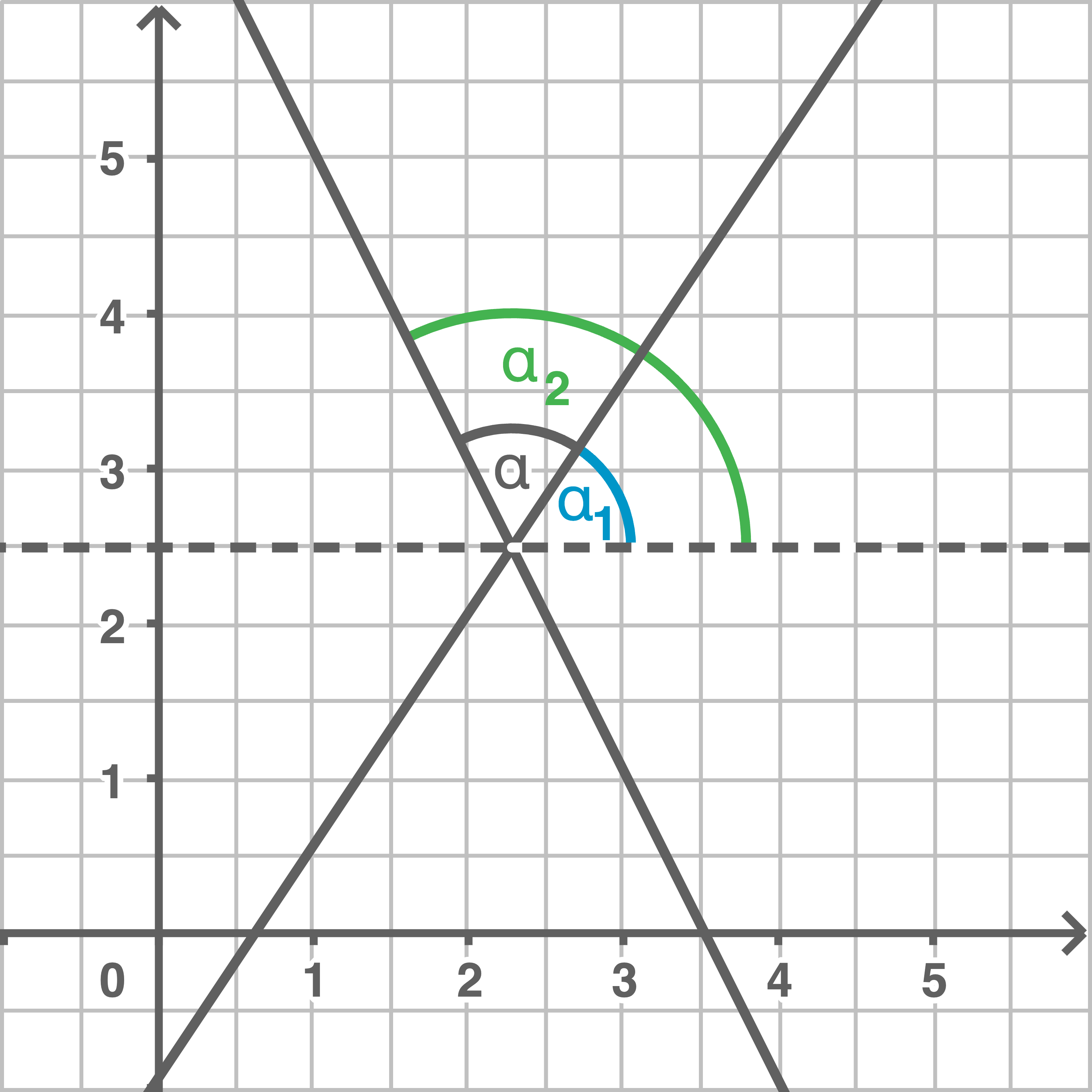
Wenn sich zwei Geraden schneiden, entstehen zwei mögliche Winkel als Schnittwinkel.
Der Schnittwinkel 
ist dann definiert als der kleinere der beiden Winkel und es gilt:
Dieser kann durch Einzeichnen einer zur 
-Achse parallelen Hilfsgeraden berechnet werden:
1
a)
Zeichne die Geraden in ein geeignetes Koordinatensystem und berechne jeweils den Anstiegswinkel.
![\(\begin{array}[t]{rll}
g_1: & y&=& \dfrac{1}{2}x+2& \\[5pt]
g_2: & y&=& 2x+1 & \\[5pt]
g_3: & y&=& x-2
\end{array}\)](https://mathjax.schullv.de/40c61dc50e907b77b988e12b2ac68f7dbd84b8d0bb1e2a2eca20db4dffebeba3?color=5a5a5a)
b)
Berechne den Schnittwinkel der beiden Geraden 
und 
2
Bestimme eine Gleichung der Geraden, die durch den Punkt 
verläuft und einen Anstiegswinkel von 
besitzt.
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
Geraden einzeichnen
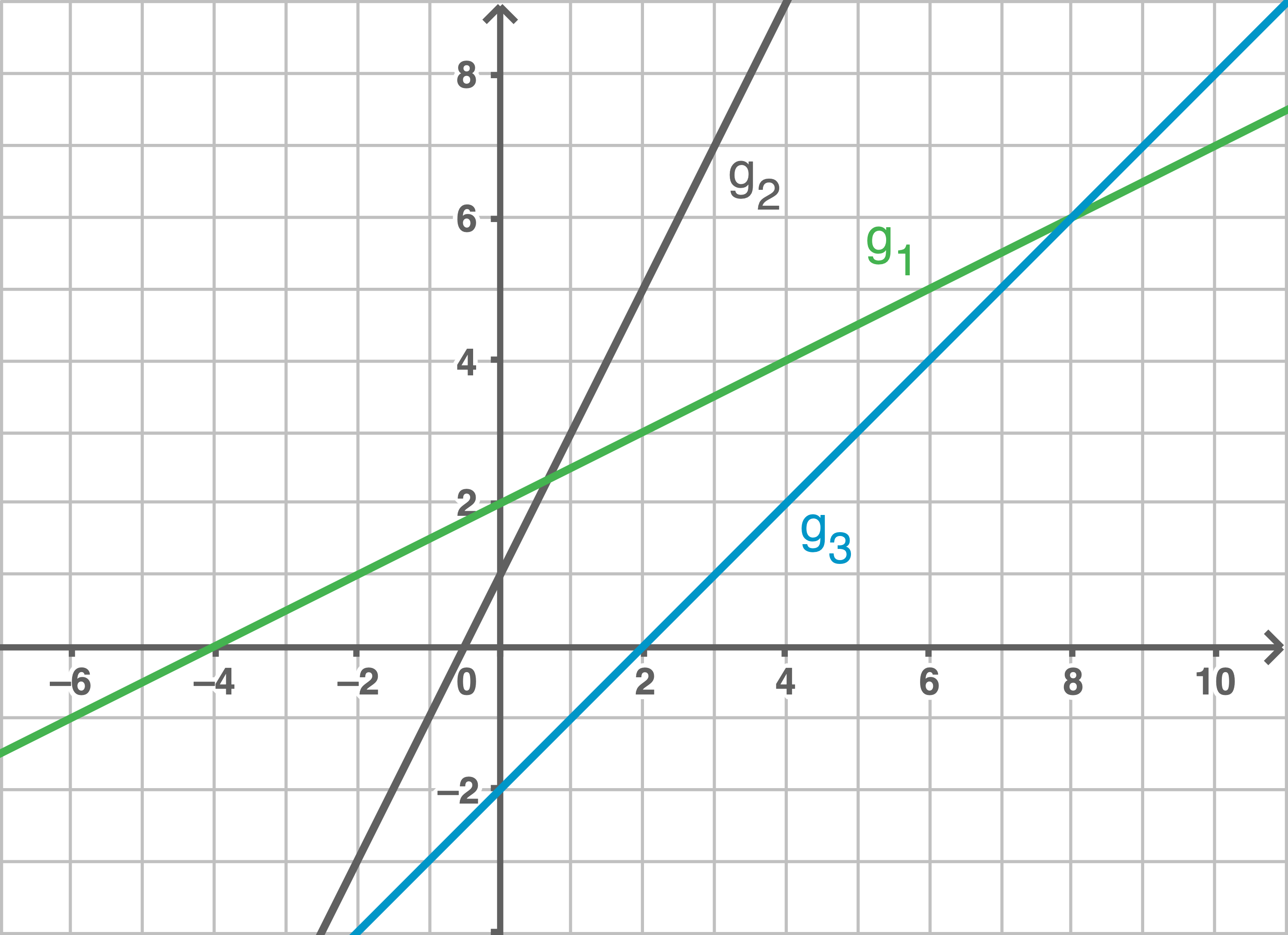Anstiegswinkel berechnen
Die Anstiege der Geraden können aus den Gleichungen abgelesen werden. Mit der Formel 
zur Berechnung des Anstiegswinkel folgt:
![\(\begin{array}[t]{rll}
g_1:& \dfrac{1}{2}&=& \tan(\alpha_1)&\quad \scriptsize \mid\; \tan^{-1} \\[5pt]
&26,57^\circ&=& \alpha_1
\end{array}\)](https://mathjax.schullv.de/defc0c660dd40fac6058da4aeb4124484bb8db991db3623548cba2a7f27d0234?color=5a5a5a)
![\(\begin{array}[t]{rll}
g_2:&2&=& \tan(\alpha_2)&\quad \scriptsize \mid\; \tan^{-1} \\[5pt]
&63,43^\circ&=& \alpha_2
\end{array}\)](https://mathjax.schullv.de/98c4a4935318f70bc5bb1619957d71243374999842c1b417e594ff2bcd23f987?color=5a5a5a)
![\(\begin{array}[t]{rll}
g_3:& 1&=& \tan(\alpha_3)&\quad \scriptsize \mid\; \tan^{-1} \\[5pt]
& 45^\circ&=& \alpha_3
\end{array}\)](https://mathjax.schullv.de/f371d134aebe7f4676cece0e41eda81b409002308cbc8329bae883518bace23f?color=5a5a5a)
b)
Für den Schnittwinkel der Geraden und 
gilt:
![\(\begin{array}[t]{rll}
\alpha&=& \alpha_2-\alpha_1&\\[5pt]
&=& 63,43^\circ-26,57^\circ &\\[5pt]
&=& 36,86 ^\circ
\end{array}\)](https://mathjax.schullv.de/a92b80215abef9a58edefa0e14f5d7b60826fe7055b819b04a396fb044b5f568?color=5a5a5a)
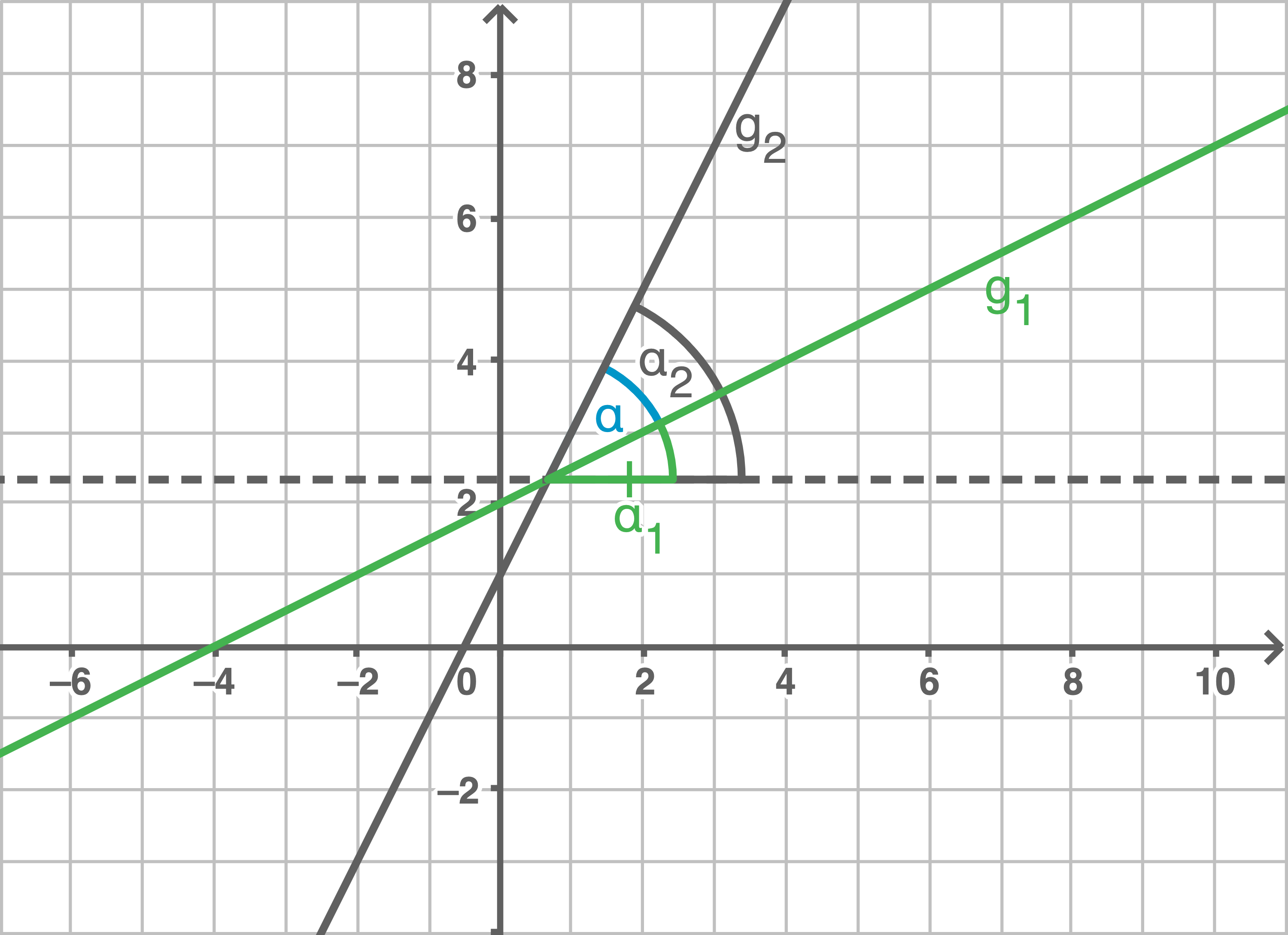
Hilfsskizze
2
Anstieg der Geraden berechnen:
![\(\begin{array}[t]{rll}
m&=& \tan(\alpha)&\\[5pt]
&=& \tan(135^\circ)&\\[5pt]
&=& -1
\end{array}\)](https://mathjax.schullv.de/633e8ade9fbb0b0d7b18ea3efe9a5950fcda4e33089479ae22443d71c7439709?color=5a5a5a)
Einsetzen des Anstiegs in die allgemeine Geradengleichung ergibt:
Da die Gerade durch den Punkt 
verläuft, gilt außerdem:
![\(\begin{array}[t]{rll}
y&=& -x+c&\quad \scriptsize \mid\; (2\mid 3) \\[5pt]
3&=& -2+c&\quad \scriptsize \mid\; +2\\[5pt]
5&=& c
\end{array}\)](https://mathjax.schullv.de/b82b205366da317a5ac08e14bf8b961c004dd2c133bd6e3f06213bd05be48a27?color=5a5a5a)
Eine Gleichung der beschriebenen Geraden folgt also mit:
