Substitutionsmethode
Definition
Eine Gleichung der FormVorgehen zum Lösen einer Gleichung durch Substitution
- Variablen substituieren
Die Variable
wird durch die Variable
(und
durch
) ersetzt.
- Quadratische Gleichung lösen Die entstandene quadratische Gleichung kann mit der Lösungsformel für quadratische Gleichungen in Normalform gelöst werden.
- Variablen resubstituieren
Die zuvor durchgeführte Substitution wird rückgängig gemacht, indem die ersetzten Variablen wieder in ihre ursprüngliche Form zurückgeführt werden. Die Variable
nach der aufgelöst wurde, wird also wieder durch die Variable
(und
durch
) ersetzt.
- Gleichung lösen
Die Lösungen der biquadratischen Gleichung ergeben sich nun durch Wurzelziehen der Resubstitution
1
Bestimme die Lösungsmenge.




a)
b)
c)
d)
2
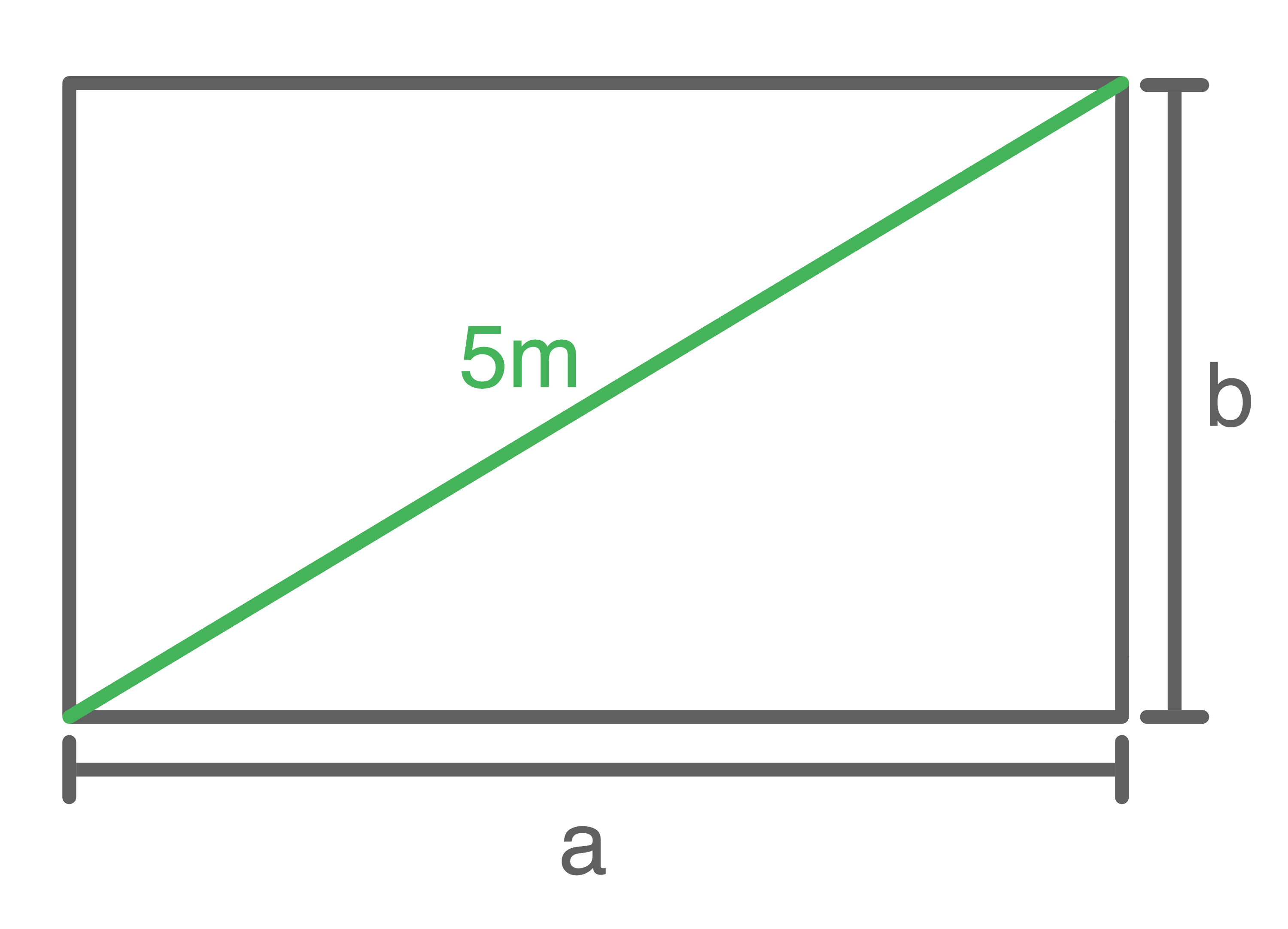
In einem Rechteck mit dem Flächeninhalt  ist die Diagonale
ist die Diagonale  lang.
Berechne die Seitenlängen des Rechtecks.
lang.
Berechne die Seitenlängen des Rechtecks.
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
b)
c)
Durch die Substitution  folgt
folgt  Mit der Lösungsformel ergeben sich die Lösungen zu:
Mit der Lösungsformel ergeben sich die Lösungen zu:
![\(\begin{array}[t]{rll}
z_1&=& -\dfrac{10}{2}+\sqrt{\left(\dfrac{10}{2}\right)^2-9} & \\[5pt]
&=& -5 + 4 & \\[5pt]
&=& -1
\end{array}\)](https://www.schullv.de/resources/formulas/ce0ba282d0295573b606fac970aed2c4a3c315f88d89ab416186a919ac95e135_light.svg)
![\(\begin{array}[t]{rll}
z_2&=& -\dfrac{10}{2}-\sqrt{\left(\dfrac{10}{2}\right)^2-9} & \\[5pt]
&=& -5-4 & \\[5pt]
&=& -9
\end{array}\)](https://www.schullv.de/resources/formulas/2a036e12f81e8e5140d99c88b193697720e8e21b2a5988dc151a0b4c5f8d6220_light.svg) Resubstitution der Variablen:
Resubstitution der Variablen:
![\(\begin{array}[t]{rll}
x^2&=& z_1 &\\[5pt]
x^2&=& -1 &\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/bcec0a13574102d2df19a3f994b578708d7e69722bd1bd8c65f23d84cf639c25_light.svg)
![\(\begin{array}[t]{rll}
x^2&=& z_2 &\\[5pt]
x^2&=& -9 &\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/c0795151b1570903dc069e19fcf1e6ca661de0a74a0b0551d829a062242d25c3_light.svg) Da die Quadratwurzel von negativen Zahlen im Bereich der reellen Zahlen nicht definiert ist, hat die biquadratische Funktion folglich keine Lösungen.
Da die Quadratwurzel von negativen Zahlen im Bereich der reellen Zahlen nicht definiert ist, hat die biquadratische Funktion folglich keine Lösungen.
d)
2
1. Schritt: Funktionsgleichung aufstellen
Für die Längen  und
und  der Seiten des Rechtecks gilt:
der Seiten des Rechtecks gilt:
![\(\begin{array}[t]{rll}
a\cdot b&=& 12 &\quad \scriptsize \mid\; :a\\[5pt]
b&=&\dfrac{12}{a}
\end{array}\)](https://www.schullv.de/resources/formulas/e7e3c3a80c1f7401cadc4e2299d674e7ac9dbf279e5dde617453f580d30183df_light.svg) Einsetzen in die dritte Bedingung liefert nun:
Einsetzen in die dritte Bedingung liefert nun:
![\(\begin{array}[t]{rll}
a^2+\left(\dfrac{12}{a}\right)^2&=& 5^2& \\[5pt]
a^2+\dfrac{144}{a^2}&=& 25&\quad \scriptsize \mid\; \cdot a^2\\[5pt]
a^4+144&=& 25a^2&\quad \scriptsize \mid\; -25a^2\\[5pt]
a^4-25a^2+144&=& 0
\end{array}\)](https://www.schullv.de/resources/formulas/c166da3d0d74ac1375b68df1295024de97fcc2260917c5b73387c5b8897bce41_light.svg) 2. Schritt: Variable substituieren
Die entstandene biquadratische Gleichung kann durch Substitution von
2. Schritt: Variable substituieren
Die entstandene biquadratische Gleichung kann durch Substitution von  durch
durch  in eine quadratische Gleichung überführt werden. Mit
in eine quadratische Gleichung überführt werden. Mit  folgt also:
folgt also:
![\(\begin{array}[t]{rll}
a^4-25a^2+144&=& 0 & \\[5pt]
(a^2)^2-25a^2+144&=& 0 &\quad \scriptsize \mid\; a^2=z\\[5pt]
z^2-25z+144&=& 0
\end{array}\)](https://www.schullv.de/resources/formulas/7f5f777b6782dc3c18782c9a0303a6bfdaf0f6b35120f8519101c8be05374380_light.svg) 3. Schritt: Quadratische Gleichung lösen
Mit der Lösungsformel für quadratische Gleichungen in Normalform und
3. Schritt: Quadratische Gleichung lösen
Mit der Lösungsformel für quadratische Gleichungen in Normalform und  sowie
sowie  ergibt sich:
ergibt sich:
![\(\begin{array}[t]{rll}
z_1&=& -\dfrac{(-25)}{2}+\sqrt{\left(\dfrac{-25}{2}\right)^2-144} & \\[5pt]
&=& 12,5+ 3,5 & \\[5pt]
&=& 16
\end{array}\)](https://www.schullv.de/resources/formulas/a8c59e8aff99a419e7da35ba8313d799288963378b49adb45f141f76ad74dcba_light.svg)
![\(\begin{array}[t]{rll}
z_2&=& -\dfrac{(-25)}{2}-\sqrt{\left(\dfrac{-25}{2}\right)^2-144} & \\[5pt]
&=& 12,5- 3,5 & \\[5pt]
&=& 9
\end{array}\)](https://www.schullv.de/resources/formulas/8aff1b0186a88978155e136072dbc9f7e846f8bcd68644f95634c9fabf3b9dcf_light.svg) 4. Schritt: Variable resubstituieren
Ersetzen von
4. Schritt: Variable resubstituieren
Ersetzen von  durch
durch  liefert:
liefert:
![\(\begin{array}[t]{rll}
a^2&=& z_1& \\[5pt]
a^2&=& 16&\quad \scriptsize \mid\; \sqrt{\;} \\[5pt]
a&=& \pm4
\end{array}\)](https://www.schullv.de/resources/formulas/87f55883be64a842ddc080b0678a749e047cab943a13e658ac403576fa251d82_light.svg)
![\(\begin{array}[t]{rll}
a^2&=& z_2& \\[5pt]
a^2&=& 9&\quad \scriptsize \mid\; \sqrt{\;} \\[5pt]
a&=& \pm3
\end{array}\)](https://www.schullv.de/resources/formulas/779f8081f19aede5d8fd134221a8edf275d40519b4e06c4844b7ea8ad26eca61_light.svg) Da
Da  gelten muss, kommen nur die positiven Lösungen
gelten muss, kommen nur die positiven Lösungen  und
und  als eine Seitenlänge des Rechtecks in Betracht.
5. Schritt: Gleichung lösen
als eine Seitenlänge des Rechtecks in Betracht.
5. Schritt: Gleichung lösen
![\(\begin{array}[t]{rll}
a\cdot b&=& 12&\quad \scriptsize \mid\; a_1=4\\[5pt]
4\cdot b&=& 12&\quad \scriptsize \mid\; :4 \\[5pt]
b&=& 3
\end{array}\)](https://www.schullv.de/resources/formulas/c4697592864a5d8f0d704333174da762e87f1d86bb1479655244a682df5e654f_light.svg)
![\(\begin{array}[t]{rll}
a\cdot b&=& 12&\quad \scriptsize \mid\; a_2=3\\[5pt]
3\cdot b&=& 12&\quad \scriptsize \mid\; :3\\[5pt]
b&=& 4
\end{array}\)](https://www.schullv.de/resources/formulas/d7a5ccaa6766d41c254b368bba2095f5442c9494fca8158c4de2f50d92b6e114_light.svg) Die Seitenlängen des Rechtecks betragen somit
Die Seitenlängen des Rechtecks betragen somit  und
und 