Linearfaktorzerlegung quadratischer Terme
Definition
Hat die quadratische Funktion mit
die Nullstellen 
und 
so ergibt sich die Linearfaktorzerlegung zu 
Die Terme 
und 
werden als Linearfaktoren des Funktionsterms bezeichnet.
Hat die quadratische Funktion 
nur eine Nullstelle 
, so gilt 
.
Hat die Funktion keine Nullstelle, so kann ihr Funktionsterm nicht in Linearfaktorzerlegung angegeben werden.
Funktionsterme quadratischer Funktionen
Der Funktionsterm einer quadratischen Gleichung kann in verschiedenen Formen angegeben werden:
- Allgemeine Form:
Aus dieser Darstellung kann der 
-Achsenabschnitt 
abgelesen werden. - Scheitelpunktform:
Aus dieser Form kann der Scheitelpunkt 
abgelesen werden. - Linearfaktorzerlegung:
Aus dem Produkt der linearen Terme können die Nullstellen und abgelesen werden.
Beispiel
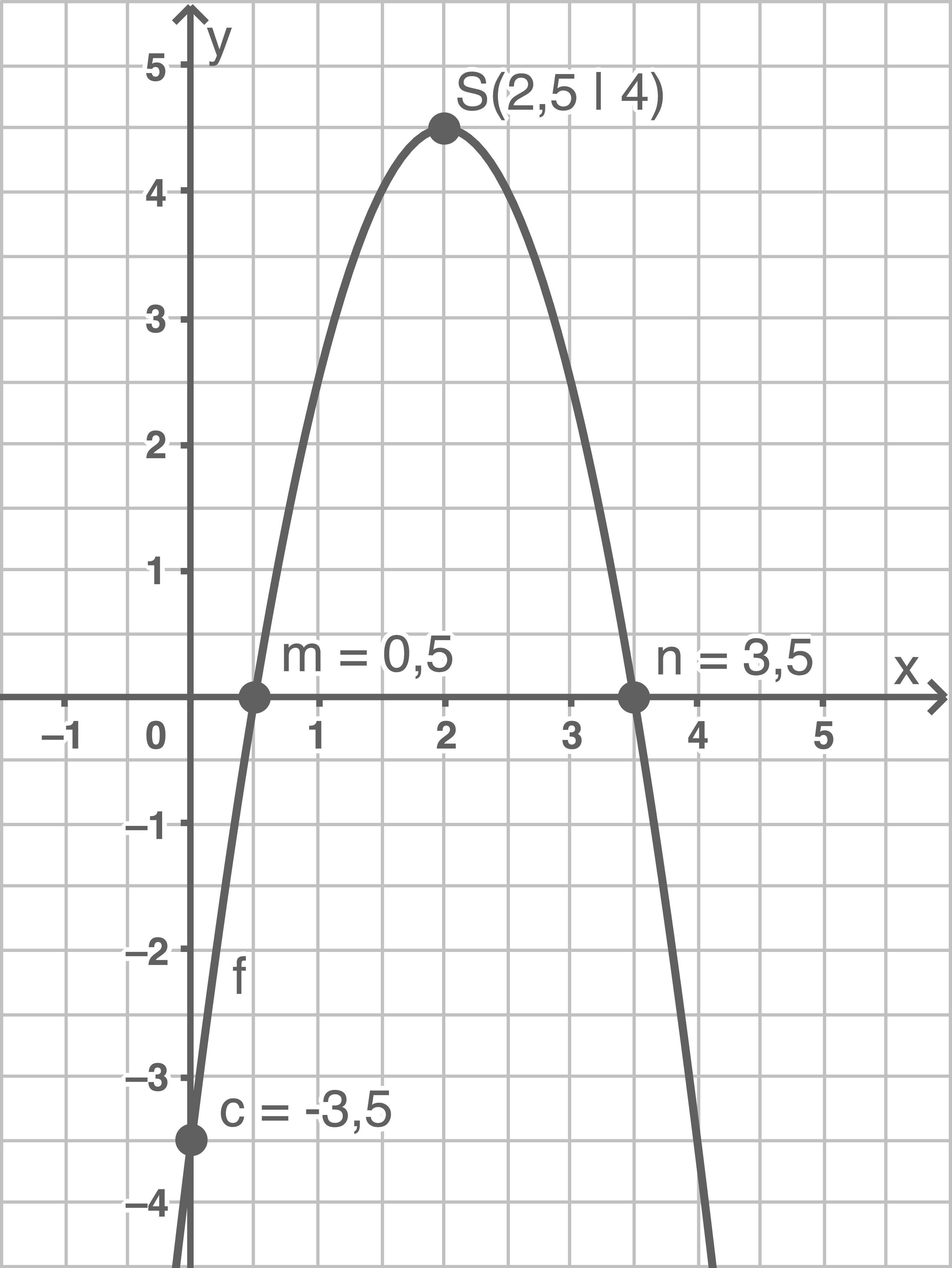
Satz von Vieta
Ist eine quadratische Gleichung in der Normalform
angegeben und die Lösungen bestimmt mit 
und 
dann gilt:
und 
Stimmen die beiden Lösungen und 
überein, so hat die Gleichung nur eine Lösung und es gilt:
und 
1
Ermittle aus den Funktionsgleichungen in Normalform die Linearfaktorzerlegungen.
a)
b)
c)
d)
2
Forme die Funktionsgleichungen in die allgemeine Form und in die Scheitelpunktform um und zeichne die dazugehörigen Graphen in ein passendes Koordinatensystem.
a)
b)
c)
Weiter lernen mit SchulLV Plus!
monatlich kündbarSchulLV Plus-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
Mit der Lösungsformel für quadratische Gleichungen in Normalform ergeben sich die Nullstellen von zu:
![\(\begin{array}[t]{rll}
x_{1;2}&=& -\dfrac{(-3)}{2}\pm\sqrt{\left(\dfrac{-3}{2}\right)^2-(-10)}& \\[5pt]
x_{1;2}&=& 1,5\pm \sqrt{1,5^2+10}& \\[5pt]
x_{1;2}&=& 1,5 \pm 3,5 & \\[5pt]
x_1&=& -2& \\[5pt]
x_2&=& 5
\end{array}\)](https://www.schullv.de/resources/formulas/e699b53cb2f094b6bcc8405ef09c47493666bd94858fe816702c430ca7a1e9f8_light.svg)
Die Linearfaktorzerlegung folgt also mit:
zu:
Die Linearfaktorzerlegung folgt also mit:
b)
Es gilt:
![\(\begin{array}[t]{rll}
f(x)&=& -x^2-8 x+9 & \\[5pt]
&=& -(x^2+8x-9) & \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/97f28c4d5823983e69cc98ca57ca5c0a5544b7c49750432132e5ab60f570170d_light.svg)
Mit der Lösungsformel für quadratische Gleichungen in Normalform folgt:
![\(\begin{array}[t]{rll}
x_{1;2}&=& -\dfrac{8}{2}\pm\sqrt{\left(\dfrac{8}{2}\right)^2-(-9)}& \\[5pt]
x_{1;2}&=& -4\pm \sqrt{16+9}& \\[5pt]
x_{1;2}&=& -4\pm 5 & \\[5pt]
x_1&=& -9& \\[5pt]
x_2&=& 1
\end{array}\)](https://www.schullv.de/resources/formulas/db499c3d6001699e6681e0ef689f10a6b8b8b749703c0318f3bf9d7e88a38002_light.svg)
Die Linearfaktorzerlegung ergibt sich also zu:
Mit der Lösungsformel für quadratische Gleichungen in Normalform folgt:
Die Linearfaktorzerlegung ergibt sich also zu:
c)
Mit der Lösungsformel für quadratische Gleichungen in Normalform ergeben sich die Nullstellen von zu:
![\(\begin{array}[t]{rll}
x_{1;2}&=& -\dfrac{4}{2}\pm\sqrt{\left(\dfrac{4}{2}\right)^2-4}& \\[5pt]
x_{1;2}&=& -2\pm \sqrt{4-4}& \\[5pt]
x_{1;2}&=& -2\pm 0& \\[5pt]
x_1&=& -2& \\[5pt]
x_2&=& -2
\end{array}\)](https://www.schullv.de/resources/formulas/413b023eeb6a3d4aa920ab01a954ff1883263d75a182df649a8a9ebade7c78ec_light.svg)
Da die Funktion also nur eine Nullstelle besitzt, gilt für die Linearfaktorzerlegung:
zu:
Da die Funktion also nur eine Nullstelle besitzt, gilt für die Linearfaktorzerlegung:
d)
Mit der Lösungsformel für quadratische Gleichungen in Normalform ergeben sich die Nullstellen von zu:
![\(\begin{array}[t]{rll}
x_{1;2}&=& -\dfrac{(-6)}{2}\pm\sqrt{\left(\dfrac{(-6)}{2}\right)^2-10}& \\[5pt]
x_{1;2}&=& 3\pm \sqrt{9-10}& \\[5pt]
x_{1;2}&=& 3\pm \sqrt{-1}& \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/bb4010c01d3e06cc43cfe1a6978abae4c52d6d277dc52405deba641f833fc459_light.svg)
Da die Wurzel einer negativen Zahl in den reellen Zahlen nicht definiert ist, besitzt die Funktion keine Nullstelle und kann somit auch nicht in Linearfaktorzerlegung angegeben werden.
zu:
Da die Wurzel einer negativen Zahl in den reellen Zahlen nicht definiert ist, besitzt die Funktion keine Nullstelle und kann somit auch nicht in Linearfaktorzerlegung angegeben werden.
2
Funktionen umformen
a)
Ausmultiplizieren ergibt:
![\(\begin{array}[t]{rll}
f(x)&=& (x-3)(x-1)& \\[5pt]
&=& x^2-1x-3x+3& \\[5pt]
&=& x^2-4x+3
\end{array}\)](https://www.schullv.de/resources/formulas/742e9b173cd620fc1309394535f81d67573b1c3c571ada72ddb9702816b3a87c_light.svg)
Die Normalform von ist somit gegeben durch 
Mit quadratischer Ergänzung folgt außerdem:
Die Scheitelpunktform folgt also mit 
Die Normalform von ist somit gegeben durch
Mit quadratischer Ergänzung folgt außerdem:
Die Scheitelpunktform folgt also mit 
![\(\begin{array}[t]{rll}
f(x)&=& x^2-4x+3 &\quad \scriptsize \mid\; +2^2 \quad \scriptsize \mid\;-2^2 \\[5pt]
&=& x^2-2\cdot 2\cdot x+2^2-2^2+3&\quad \scriptsize \mid\; \text{2. bin. Formel} \\[5pt]
&=& (x-2)^2-4+3 & \\[5pt]
&=& (x-2)^2-1
\end{array}\)](https://www.schullv.de/resources/formulas/32591983bbc43dce2d57734dea8326299372f723ff48726bccbcc1b40cdcbd42_light.svg)
b)
Ausmultiplizieren ergibt:
![\(\begin{array}[t]{rll}
g(x)&=& 2(x-2)(x+4)& \\[5pt]
&=& 2(x^2+4x-2x-8)& \\[5pt]
&=& 2x^2+4x-16
\end{array}\)](https://www.schullv.de/resources/formulas/7aeed2bd2ba771c89b5863583bdd85ddec67b8f7b891694e0a86d99644893d6d_light.svg)
Die Normalform von ist somit gegeben durch 
Mit quadratischer Ergänzung folgt außerdem:
Die Scheitelpunktform folgt also mit 
Die Normalform von ist somit gegeben durch
Mit quadratischer Ergänzung folgt außerdem:
Die Scheitelpunktform folgt also mit 
![\(\begin{array}[t]{rll}
g(x)&=& 2\cdot (x^2+2x-8)&\quad \scriptsize \mid\; +1^2 \quad \scriptsize \mid\;-1^2 \\[5pt]
&=& 2\cdot (x^2+2\cdot 1\cdot x + 1^2 -1^2 -8)& \\[5pt]
&=& 2\cdot ((x^2+2\cdot 1\cdot x + 1^2) -9)&\quad \scriptsize \mid\; \text{1. bin. Formel} \\[5pt]
&=& 2\cdot (x+1)^2-2\cdot 9 &\\[5pt]
&=& 2\cdot (x+1)^2-18
\end{array}\)](https://www.schullv.de/resources/formulas/9f138b124cb9b18d553e953be784453082d0a1124cca16a8cbdcd2a579e07762_light.svg)
c)
Ausmultiplizieren ergibt:
![\(\begin{array}[t]{rll}
h(x)&=& -\dfrac{1}{2}(x+8)(x-2)& \\[5pt]
&=& -\dfrac{1}{2}(x^2-2x+8x-16)& \\[5pt]
&=& -\dfrac{1}{2}x^2-3x+8
\end{array}\)](https://www.schullv.de/resources/formulas/37e0c88b127b433d9ab3397cb91772505e0e18cc3223f37e1ee285869fbe812c_light.svg)
Die Normalform von ist somit gegeben durch 
Mit quadratischer Ergänzung folgt außerdem:
Die Scheitelpunktform folgt also mit 
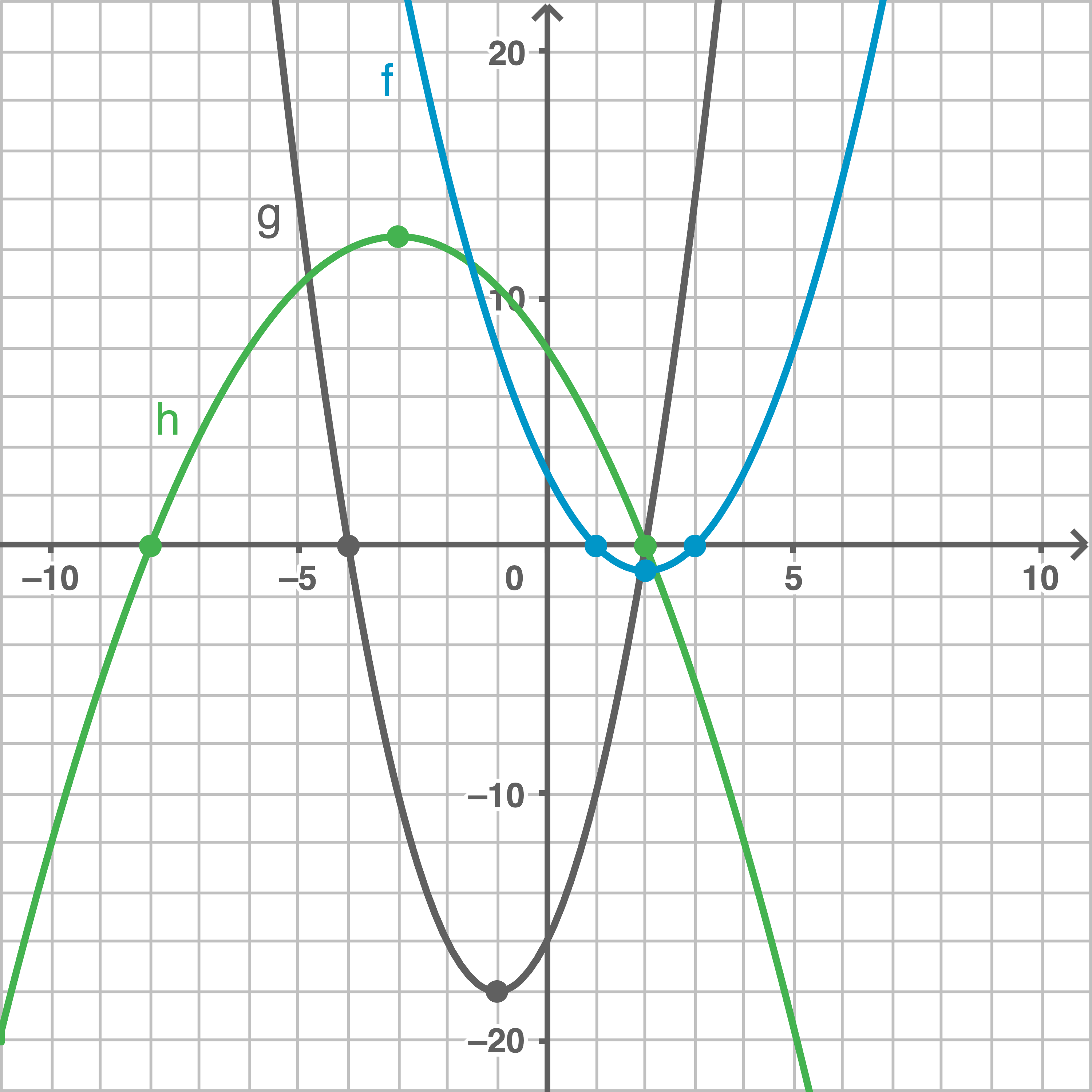
Graphen einzeichnen
Aus der Scheitelform können jeweils die Koordinaten des Scheitelpunkts abgelesen werden. Die Linearfaktorzerlegungen geben zudem die Nullstellen der Funktionen an. Somit folgt:
Die Normalform von ist somit gegeben durch
Mit quadratischer Ergänzung folgt außerdem:
Die Scheitelpunktform folgt also mit 
![\(\begin{array}[t]{rll}
h(x)&=& -\dfrac{1}{2}\cdot (x^2+6x-16)&\quad \scriptsize \mid\; +3^2 \quad \scriptsize \mid\;-3^2 \\[5pt]
&=& -\dfrac{1}{2}\cdot (x^2+2\cdot 3\cdot x + 3^2 -3^2 -16)& \\[5pt]
&=& -\dfrac{1}{2}\cdot ((x^2+2\cdot 3\cdot x + 3^2) -25)&\quad \scriptsize \mid\; \text{1. bin. Formel} \\[5pt]
&=& -\dfrac{1}{2}\cdot (x+3)^2+\dfrac{1}{2}\cdot 25 &\\[5pt]
&=& -\dfrac{1}{2}\cdot (x+3)^2+12,5
\end{array}\)](https://www.schullv.de/resources/formulas/c8b430b2cd5feab2a477aa4034af801989ec33e2ae38a59f90ecba7d1b8e9255_light.svg)