Quadratische Funktionen – Definition
Definition
Eine FunktionBeispiel: Maximierungsproblem
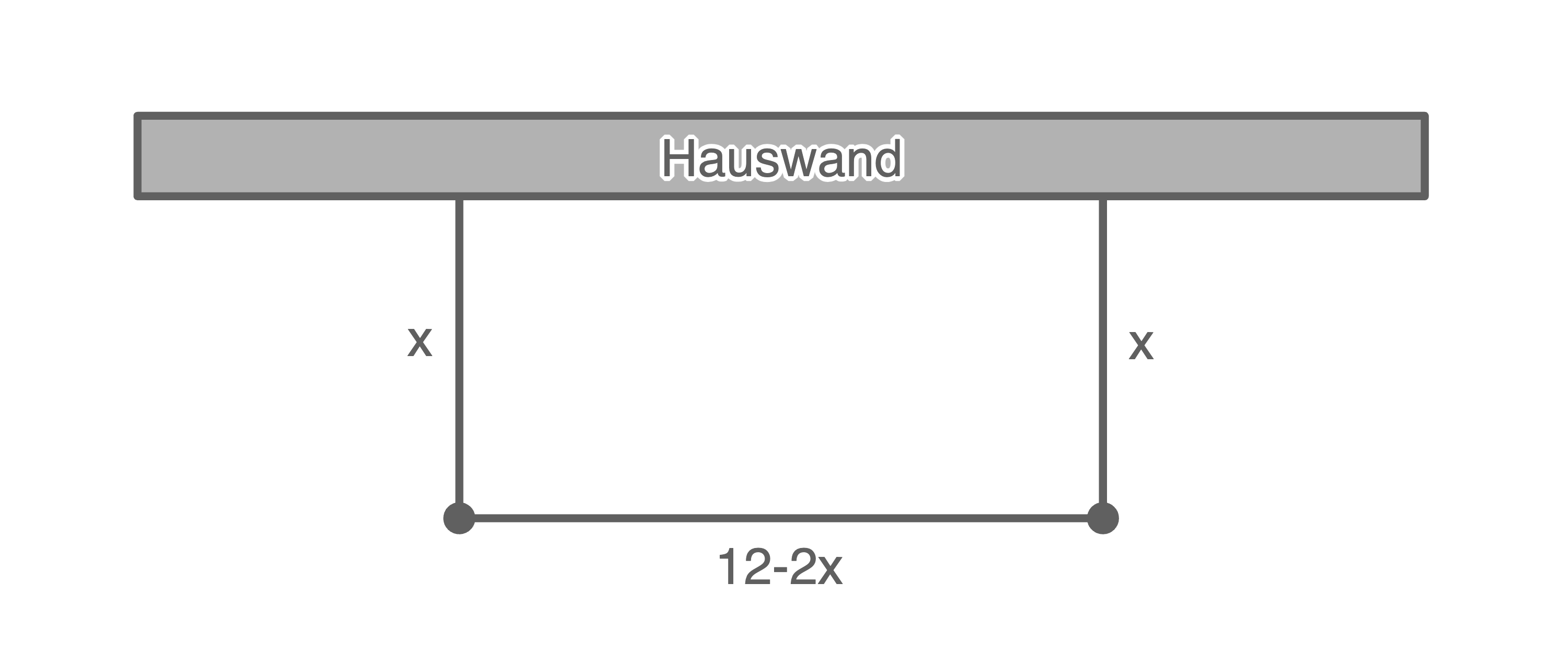
Entlang einer Hauswand soll ein rechteckiger Gemüsegarten mit einem Holzzaun abgegrenzt werden. Das Budget reicht für genau 12 Meter Holzzaun. Berechne, in welchem Abstand von der Hauswand die Eckpfosten des Zauns gesetzt werden müssen, sodass der Gemüsegarten eine möglichst große Fläche hat. 1. Schritt: Funktionsgleichung aufstellen
Da eine Seite des Rechtecks bereits durch die Hauswand abgegrenzt ist, müssen die restlichen drei Seiten insgesamt eine Länge von 12 Metern haben. Wird der Abstand eines Eckpfostens zur Hauswand als  bezeichnet, so bleibt für den Abstand der beiden Pfosten zueinander eine Zaunlänge von
bezeichnet, so bleibt für den Abstand der beiden Pfosten zueinander eine Zaunlänge von  übrig.
übrig.
 Für den Flächeninhalt des rechteckigen Gemüsegartens gilt also:
Für den Flächeninhalt des rechteckigen Gemüsegartens gilt also:
![\(\begin{array}[t]{rll}
A&=& x\cdot (12-2x) & \\[5pt]
&=& 12x-2x^2
\end{array}\)](https://www.schullv.de/resources/formulas/ff5e25eeeaa9cd4011778b57bb92f95d3984da5b82e1e07112a5140b13d69172_light.svg) Da der Abstand der beiden Pfosten von der Hauswand nicht Null oder negativ sein kann, gilt
Da der Abstand der beiden Pfosten von der Hauswand nicht Null oder negativ sein kann, gilt  Da die beiden Abstände außerdem zusammen nicht größer als die vorgegebene Zaunlänge sein können, gilt
Da die beiden Abstände außerdem zusammen nicht größer als die vorgegebene Zaunlänge sein können, gilt  also
also 
2. Schritt: Maximalen Flächeninhalt bestimmen

Hilfsskizze
(nicht maßstäblich)
(nicht maßstäblich)
Um den Abstand  zu finden, für den der Flächeninhalt
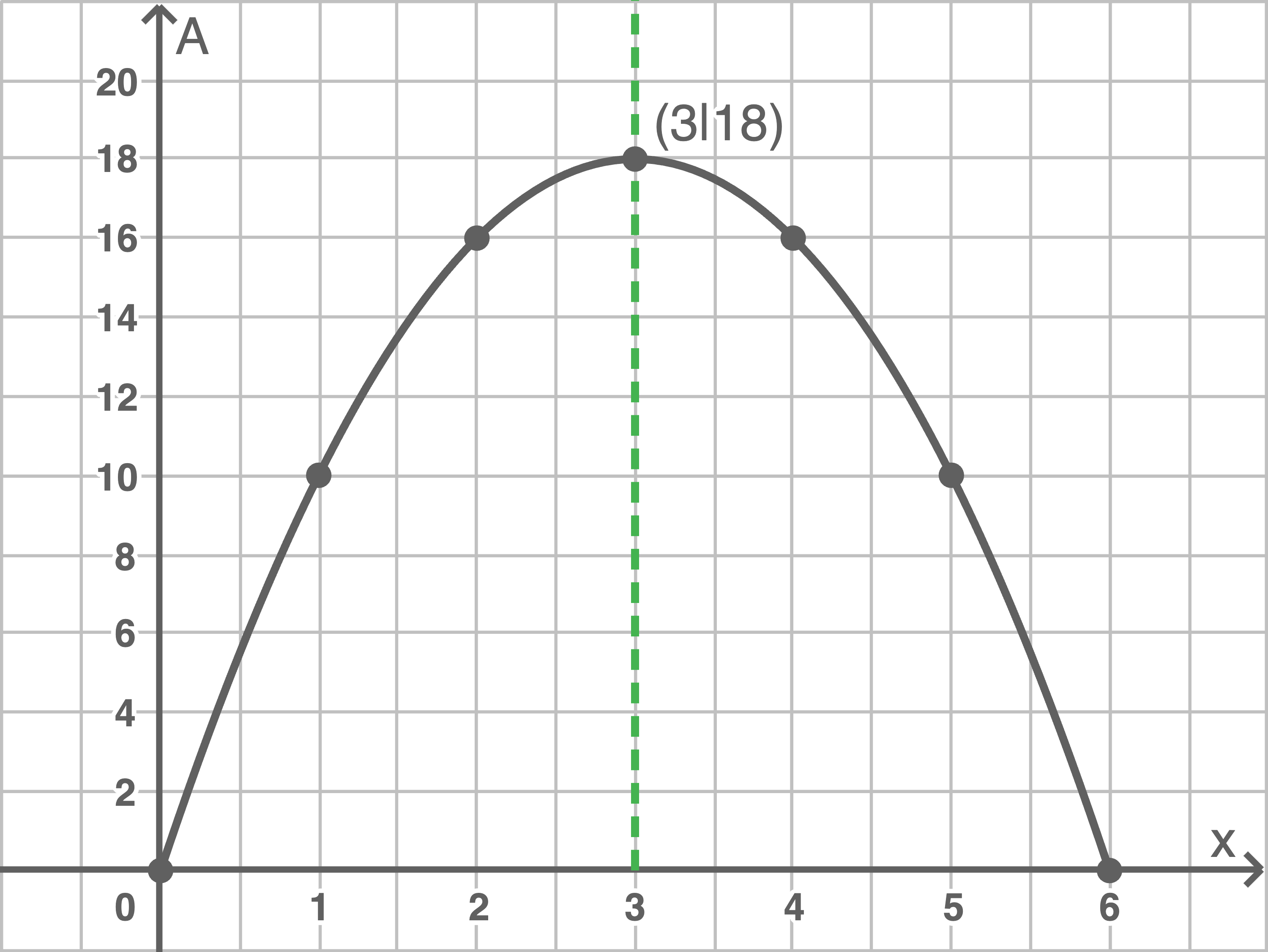
zu finden, für den der Flächeninhalt  am größten ist, kann mit Hilfe einer Wertetabelle der entsprechende Graph gezeichnet werden. Zum besseren Zeichnen können die Randwerte hinzugenommen werden.
am größten ist, kann mit Hilfe einer Wertetabelle der entsprechende Graph gezeichnet werden. Zum besseren Zeichnen können die Randwerte hinzugenommen werden.
Der Graph ist symmetrisch und hat seinen höchsten Punkt an der Stelle  Der zugehörige Funktionswert ist 18.
Die Eckpfosten müssen also 3 Meter von der Hauswand und somit
Der zugehörige Funktionswert ist 18.
Die Eckpfosten müssen also 3 Meter von der Hauswand und somit  voneinander entfernt gesetzt werden, sodass der Gemüsegarten den größtmöglichen Flächeninhalt von
voneinander entfernt gesetzt werden, sodass der Gemüsegarten den größtmöglichen Flächeninhalt von  besitzt.
besitzt.
1
Ein Architekt plant, ein Modell eines quaderförmigen Gebäudes mit quadratischer Grundfläche aus einem Drahtstück mit einer Länge von 4 Metern zu erstellen.
Bestimme die Abmessungen des Gebäudes so, dass der Oberflächeninhalt möglichst groß ist.
2
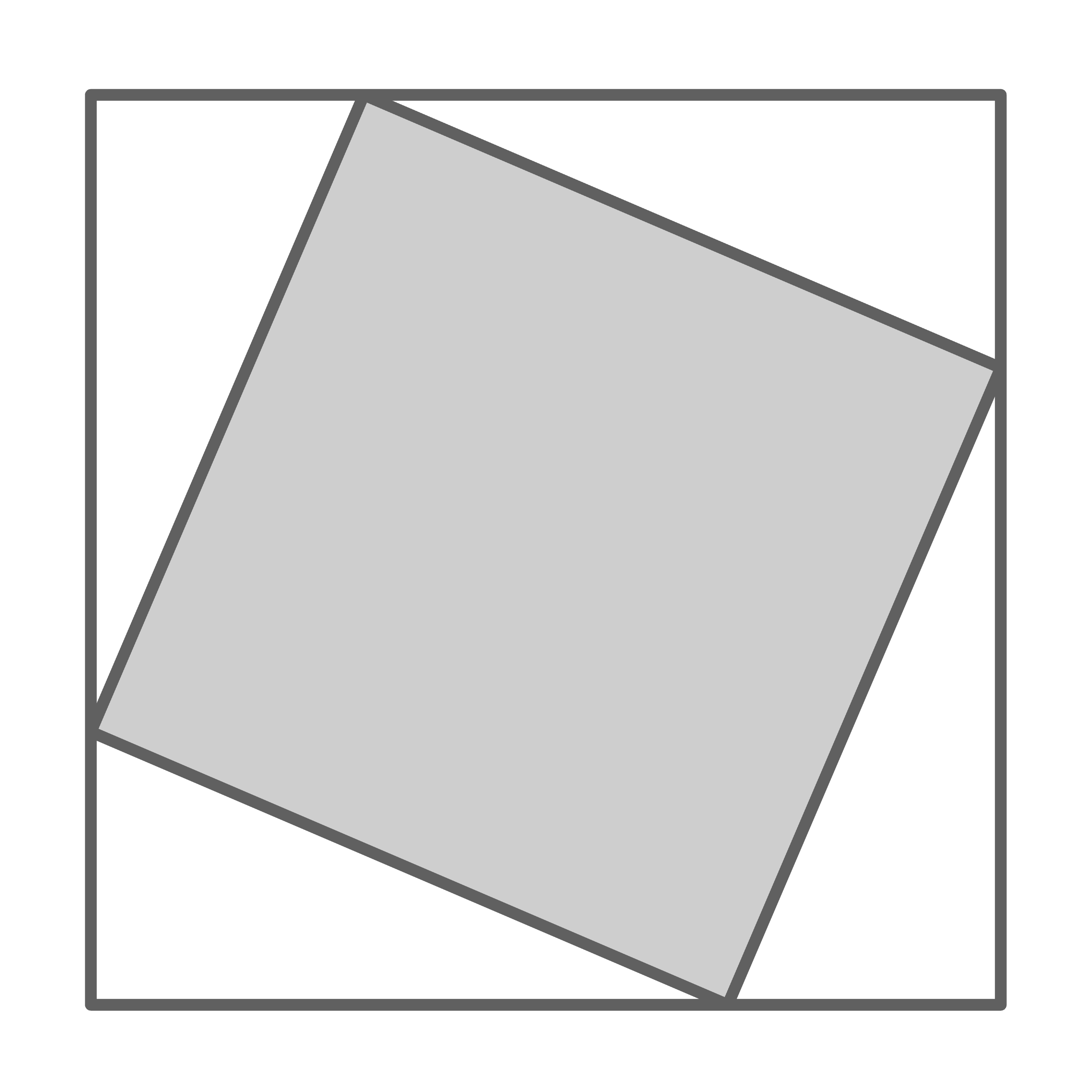
Die quadratische Grundfläche eines Gebäudes soll mit einem Mosaikboden gestaltet werden.
Die Seitenlänge der Grundfläche beträgt  In diese Fläche soll gekippt ein kleineres Quadrat mit vergoldeten Fließen eingefügt werden.
Um den Verbrauch an goldenen Fließen zu minimieren, soll das innere Quadrat möglichst klein sein. Für welche Lage des inneren Quadrats ist dieses am kleinsten?
In diese Fläche soll gekippt ein kleineres Quadrat mit vergoldeten Fließen eingefügt werden.
Um den Verbrauch an goldenen Fließen zu minimieren, soll das innere Quadrat möglichst klein sein. Für welche Lage des inneren Quadrats ist dieses am kleinsten?
Hilfsskizze
(nicht maßstäblich)
(nicht maßstäblich)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
1. Schritt: Funktionsgleichung aufstellen
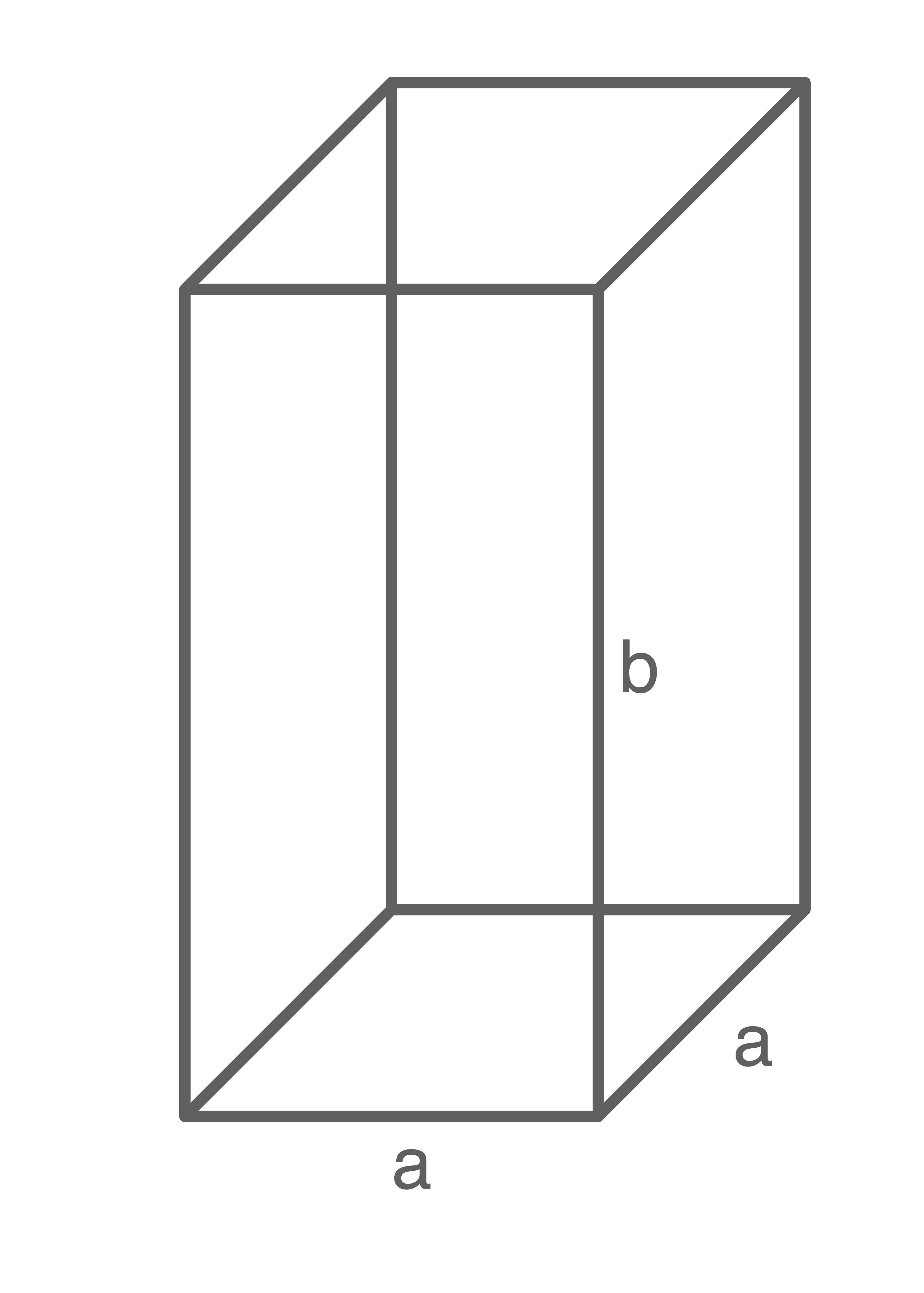 Für den Oberflächeninhalt eines Quaders mit quadratischer Grundfläche gilt:
Für den Oberflächeninhalt eines Quaders mit quadratischer Grundfläche gilt:
 Da der Draht eine Länge von 4 Metern hat, darf die gesamte Kantenlänge diesen Wert nicht überschreiten:
Da der Draht eine Länge von 4 Metern hat, darf die gesamte Kantenlänge diesen Wert nicht überschreiten:
![\(\begin{array}[t]{rll}
4&=& 8a+4b &\quad \scriptsize \mid\; -8a \\[5pt]
4-8a&=& 4b &\quad \scriptsize \mid\; :4 \\[5pt]
1-2a&=& b
\end{array}\)](https://www.schullv.de/resources/formulas/f039cdbfe721776beaccae6378689c4136486d15b30bafe9646cd09b95757eb4_light.svg) Es muss somit
Es muss somit  gelten.
Der Oberflächeninhalt kann also mit folgender Formel berechnet werden:
gelten.
Der Oberflächeninhalt kann also mit folgender Formel berechnet werden:
![\(\begin{array}[t]{rll}
O&=& 2a^2+4a\cdot (1-2a)&\\[5pt]
&=& 2a^2+4a-8a^2&\\[5pt]
&=& -6a^2+4a
\end{array}\)](https://www.schullv.de/resources/formulas/bec004a69a2514637531f2a36798099b044365477aaa2071c9089f859fae007b_light.svg) Da die Kantenlänge
Da die Kantenlänge  der Grundfläche nicht null oder negativ sein kann, muss
der Grundfläche nicht null oder negativ sein kann, muss  gelten. Die Summe der Kantenlängen darf außerdem nicht größer als
gelten. Die Summe der Kantenlängen darf außerdem nicht größer als  sein. Da die Kantenlänge
sein. Da die Kantenlänge  im Quader genau acht mal vorkommt, muss also auch
im Quader genau acht mal vorkommt, muss also auch  und somit
und somit  gelten.
2. Schritt: Maximalen Oberflächeninhalt bestimmen
gelten.
2. Schritt: Maximalen Oberflächeninhalt bestimmen

Hilfsskizze
(nicht maßstäblich)
(nicht maßstäblich)
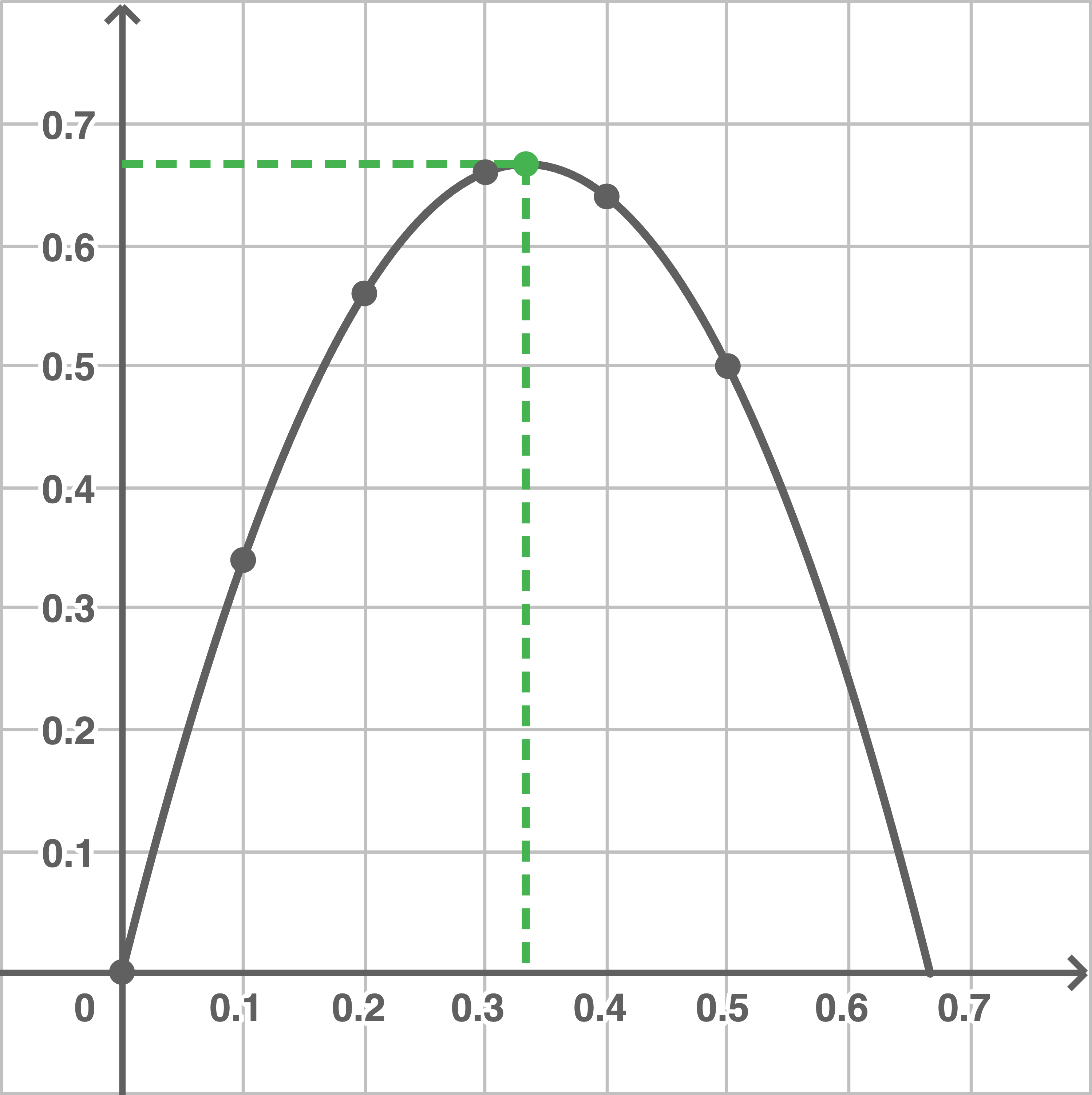
Um die Kantenlänge  der Grundfläche zu finden, für die der Oberflächeninhalt
der Grundfläche zu finden, für die der Oberflächeninhalt  am größten ist, kann mit Hilfe einer Wertetabelle der entsprechende Graph gezeichnet werden. Zum besseren Zeichnen können die Randwerte hinzugenommen werden.
am größten ist, kann mit Hilfe einer Wertetabelle der entsprechende Graph gezeichnet werden. Zum besseren Zeichnen können die Randwerte hinzugenommen werden.

Der Graph hat seinen höchsten Punkt etwa an der Stelle  Der zugehörige Funktionswert ist ungefähr 0,67.
Die Breite und Länge des Gebäudes müssen im Modell somit etwa
Der zugehörige Funktionswert ist ungefähr 0,67.
Die Breite und Länge des Gebäudes müssen im Modell somit etwa  und die Höhe dementsprechend
und die Höhe dementsprechend  betragen, sodass das Modell einen größtmöglichen Oberflächeninhalt von
betragen, sodass das Modell einen größtmöglichen Oberflächeninhalt von  besitzt.
Dies bedeutet, dass der Oberflächeninhalt des Quaders genau dann am größten ist, wenn alle Kantenlängen gleich groß sind. Das Modell entspricht in diesem Fall also einem Würfel.
besitzt.
Dies bedeutet, dass der Oberflächeninhalt des Quaders genau dann am größten ist, wenn alle Kantenlängen gleich groß sind. Das Modell entspricht in diesem Fall also einem Würfel.
2
1. Schritt: Funktionsgleichung aufstellen
Aufgrund der Symmetrie teilen die Eckpunkte des kleinen Quadrats die Seiten des großen Quadrats jeweils in gleich lange Abschnitte. Da die Seitenlänge des äußeren, größeren Quadrats  beträgt, ergeben sich für die beiden unterteilten Abschnitte jeweils die Längen
beträgt, ergeben sich für die beiden unterteilten Abschnitte jeweils die Längen  und
und 
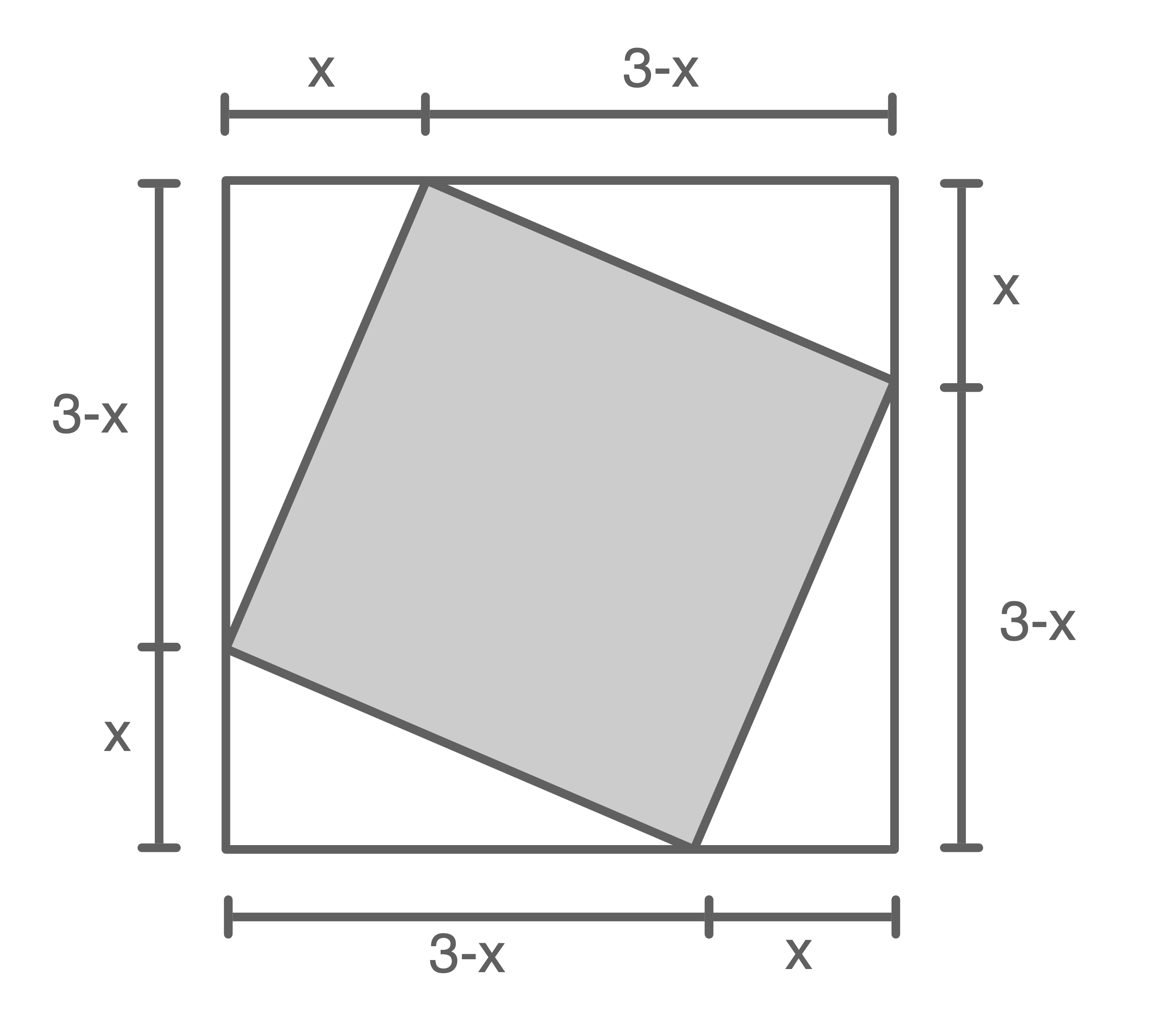 Die dabei entstehenden rechtwinkligen Dreiecke zwischen den beiden Quadraten sind kongruent zueinander. Für ihren Flächeninhalt gilt:
Die dabei entstehenden rechtwinkligen Dreiecke zwischen den beiden Quadraten sind kongruent zueinander. Für ihren Flächeninhalt gilt:
 Der Flächeninhalt des kleineren Quadrats ergibt sich nun aus dem Flächeninhalt des größeren Quadrats, von welchem der Flächeninhalt der vier kongruenten Dreiecke abgezogen wird. Es ergibt sich:
Der Flächeninhalt des kleineren Quadrats ergibt sich nun aus dem Flächeninhalt des größeren Quadrats, von welchem der Flächeninhalt der vier kongruenten Dreiecke abgezogen wird. Es ergibt sich:
![\(\begin{array}[t]{rll}
A&=& 3^2-4\cdot A_Δ&\\[5pt]
&=& 3^2-4\cdot \dfrac{1}{2}\cdot x\cdot (3-x) &\\[5pt]
&=& 9-2x\cdot (3-x)&\\[5pt]
&=& 9-6x+2x^2&\\[5pt]
&=& 2x^2-6x+9
\end{array}\)](https://www.schullv.de/resources/formulas/046e443ee54b8af704bfd01b35ccb6a2676cdf7c6ce430e66418ca8878f11266_light.svg) Da die Seitenlänge des äußeren Quadrats
Da die Seitenlänge des äußeren Quadrats  beträgt, muss auch
beträgt, muss auch  gelten.
gelten.
2. Schritt: Minimalen Flächeninhalt bestimmen

Hilfsskizze
(nicht maßstäblich)
(nicht maßstäblich)
Um die Länge  zu bestimmen, für die der Flächeninhalt des kleineren Quadrats minimal ist, kann mit Hilfe einer entsprechenden Wertetabelle der Graph für den Flächeninhalt
zu bestimmen, für die der Flächeninhalt des kleineren Quadrats minimal ist, kann mit Hilfe einer entsprechenden Wertetabelle der Graph für den Flächeninhalt  in Abhängigkeit von
in Abhängigkeit von  gezeichnet und dessen Tiefpunkt bestimmt werden. Zum vereinfachten Zeichnen können die Randwerte hinzugenommen werden, auch wenn diese im Sachzusammenhang bedeutungslos sind.
gezeichnet und dessen Tiefpunkt bestimmt werden. Zum vereinfachten Zeichnen können die Randwerte hinzugenommen werden, auch wenn diese im Sachzusammenhang bedeutungslos sind.
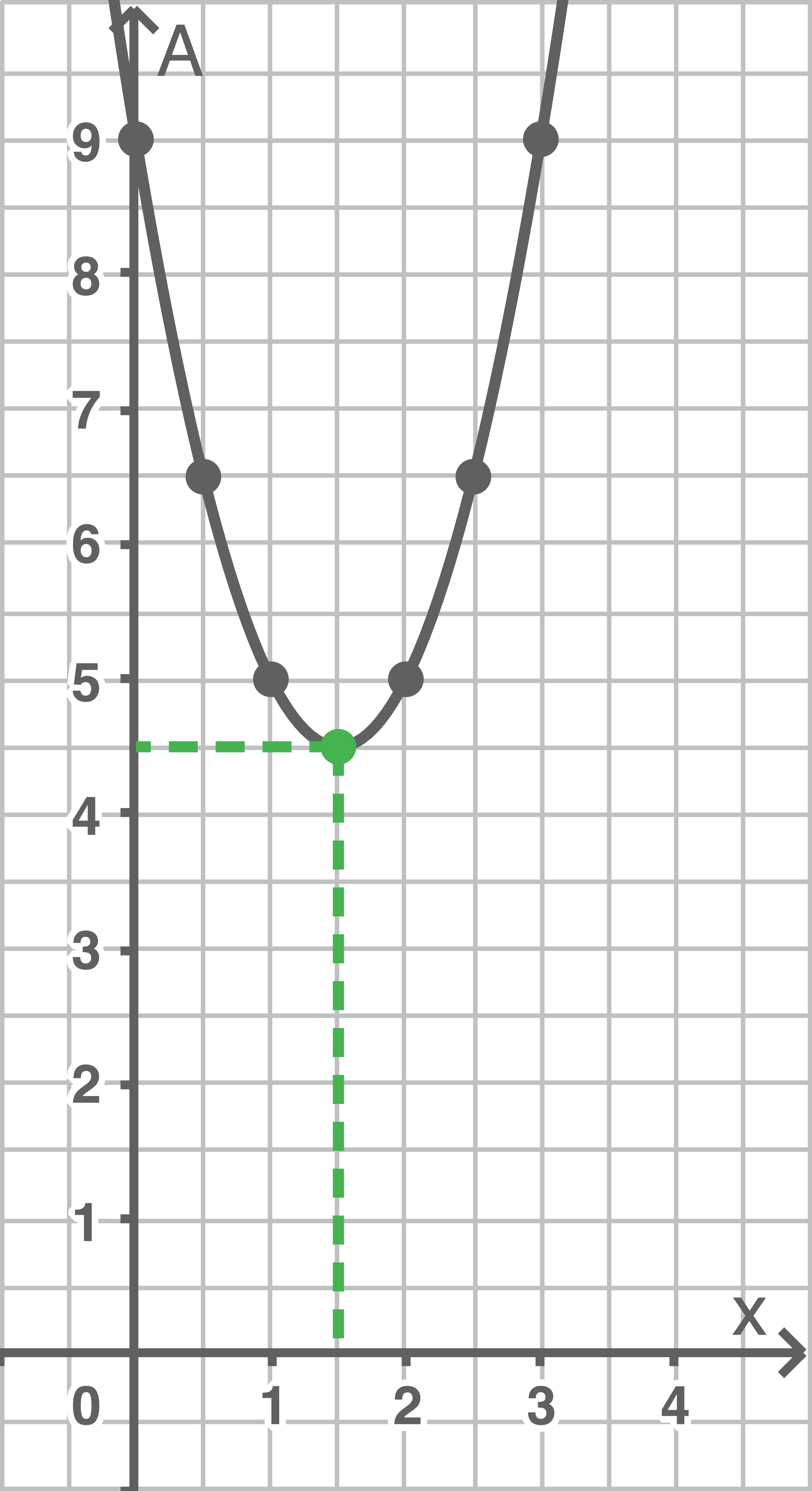
Der Graph ist symmetrisch und hat seinen tiefsten Punkt an der Stelle  Der zugehörige Funktionswert ist 4,5.
Für die Unterteilung in die Abschnitte
Der zugehörige Funktionswert ist 4,5.
Für die Unterteilung in die Abschnitte  und
und  ist der Flächeninhalt mit einem Wert von
ist der Flächeninhalt mit einem Wert von  am kleinsten.
Die Eckpunkte des inneren Quadrats unterteilen die Seiten des äußeren Quadrats somit jeweils genau in der Hälfte und stellen deren Mittelpunkte dar.
am kleinsten.
Die Eckpunkte des inneren Quadrats unterteilen die Seiten des äußeren Quadrats somit jeweils genau in der Hälfte und stellen deren Mittelpunkte dar.