Optimierungsprobleme mit quadratischen Funktionen
Ein Optimierungsproblem ist ein mathematisches Problem, bei dem eine Größe maximiert oder minimiert werden soll, die von einer oder mehreren Variablen abhängt und bestimmte Bedingungen erfüllen soll.
Definition
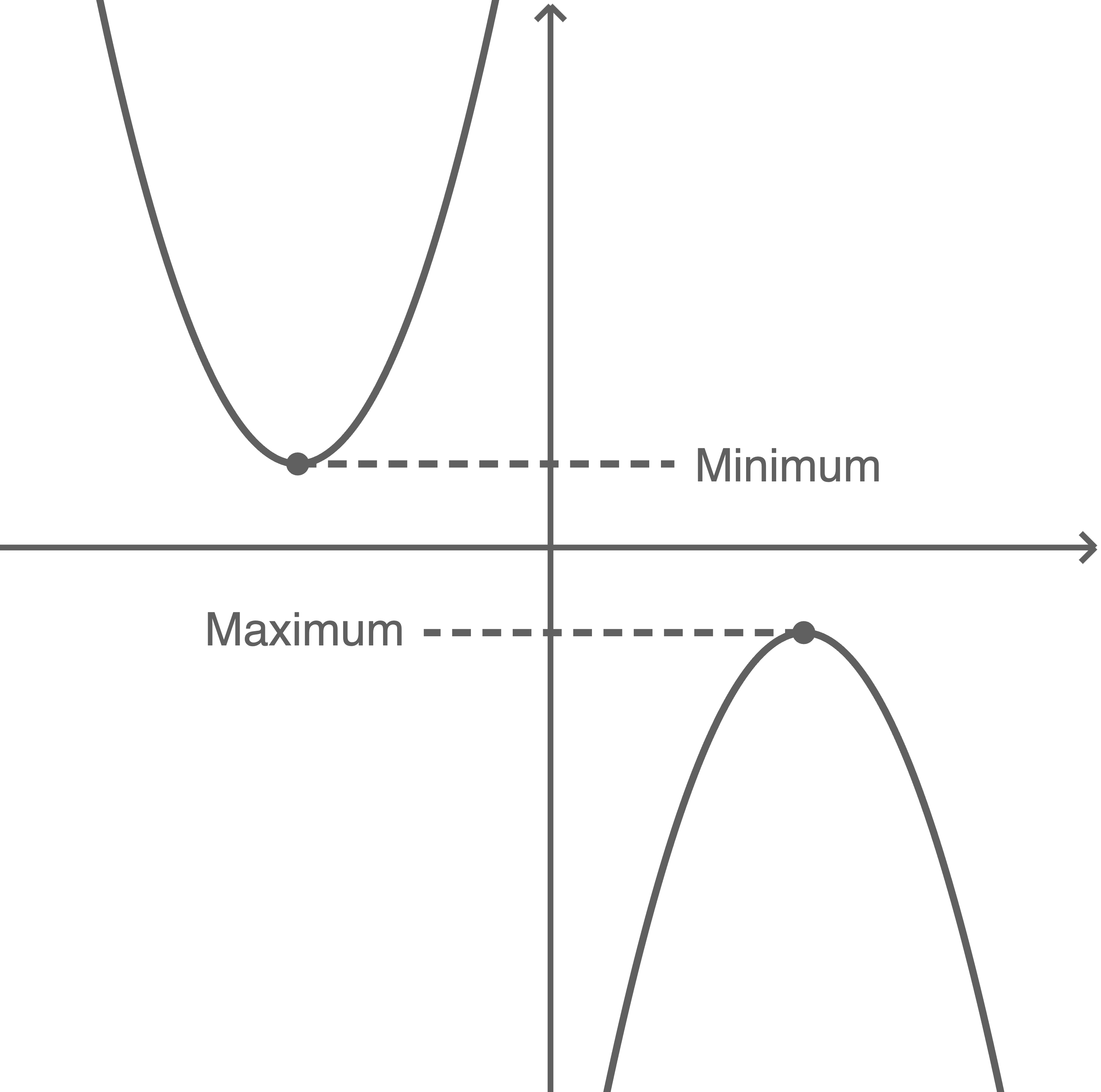
Ist der Graph einer quadratischen Funktion eine nach oben geöffnete Parabel, so entspricht der Scheitelpunkt dem Tiefpunkt des Graphen. Die 
-Koordinate des Tiefpunkts ist somit der kleinstmögliche Funktionswert und wird als Minimum der Funktion bezeichnet.
Hat eine quadratische Funktion eine nach unten geöffnete Parabel als Graphen, so ist deren Scheitelpunkt der Hochpunkt. Die -Koordinate des Hochpunkts ist somit der größtmögliche Funktionswert und wird als Maximum bezeichnet.
Der Überbegriff Extremwert umfasst die beiden Begriffe Minimum und Maximum.
Lösungsstrategien
Der Extremwert einer quadratischen Funktion kann mit unterschiedlichen Methoden bestimmt werden:- Tabellarisch Durch systematisches Probieren kann eine Wertetabelle erstellt und aus dieser ein Näherungswert für den Extremwert abgelesen werden. Umso kleiner die Schritte, desto genauer der Näherungswert.
- Grafisch
Da der Extremwert bei quadratischen Funktionen der
- Algebraisch
Mit der Funktionsgleichung kann der Extremwert auf zwei Weisen bestimmt werden:
- Aus der Scheitelpunktform
können die Koordinaten des Scheitelpunkts
direkt abgelesen werden. Die
entspricht dann dem Extremwert.
- Besitzt die quadratische Funktion zwei Nullstellen, so liegt die
-Koordinate des Scheitelpunkts aufgrund der Symmetrie genau in deren Mitte. Berechnen der
- Aus der Scheitelpunktform
1
Ein Fitnessstudio hat 150 Mitglieder, die monatlich 40€ für die Mitgliedschaft zahlen. Das Management plant eine Preissenkung, um die Mitgliederzahl zu steigern. Es wird erwartet, dass für jede Senkung um 5 € die Mitgliederzahl um 30 zunimmt.
Ermittle algebraisch den optimalen Preis, um die Einnahmen zu maximieren.
2
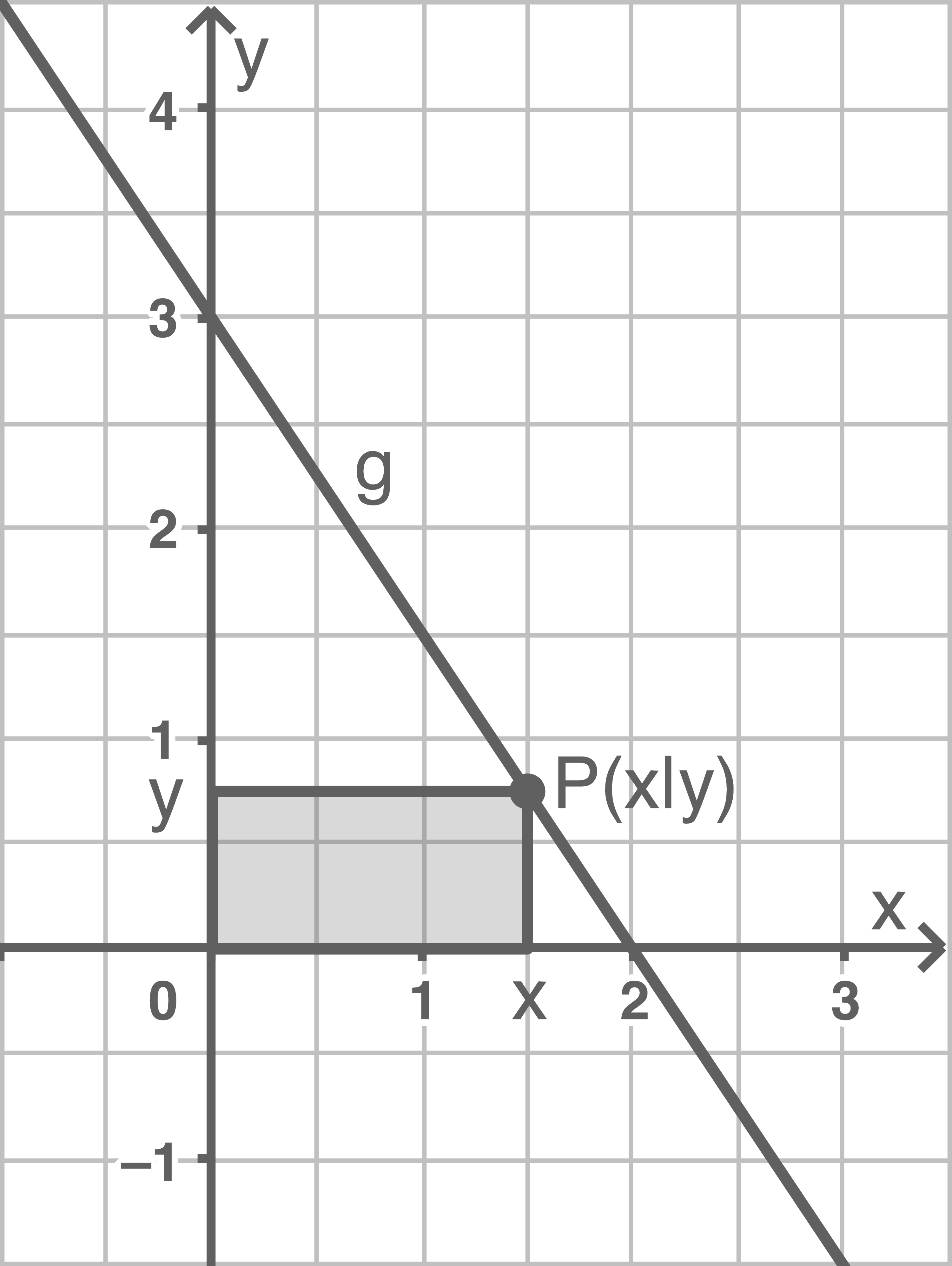
Ein Rechteck soll im Koordinatensystem so positioniert werden, dass es mit dem Ursprung 
und einem Punkt 
auf der Geraden 
mit 
den größtmöglichen Flächeninhalt hat.
Berechne die Koordinaten von 
für die der maximale Flächeninhalt erreicht wird.
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
Wird der Preis für eine Mitgliedschaft -fach um 
gesenkt, so gilt für den neuen Betrag in 
Da die Mitgliederzahl gleichzeitig -mal um 30 zunimmt, gilt für diese nach der Peissenkung:
Die Gesamteinnahmen nach einer -fachen Preissenkung um je ergeben sich also mit:
Die Koordinaten des Scheitelpunkts dieser quadratischen Funktion können auf zwei Weisen bestimmt werden:
1. Möglichkeit: Umformen zur Scheitelpunktform
Durch Ausmultiplizieren und quadratische Ergänzung ergibt sich:
Aufgrund des negativen Vorzeichens ist die Parabel nach unten geöffnet. Der Scheitelpunkt 
ist somit der höchste Punkt der Parabel.
Wird der Preis also um 
pro Monat gesenkt, so werden mit einer monatlichen Gebühr von 
und 
Mitgliedern maximale Einnahmen von 
erzielt.
2. Möglichkeit: Berechnung mit Hilfe der Nullstellen
An den Nullstellen gilt:
Der Term wird genau dann null, wenn einer der beiden Faktoren null ist:
![\(\begin{array}[t]{rll}
40-5x_1&=& 0&\quad \scriptsize \mid\; +5x_1 \\[5pt]
40&=& 5x_1&\quad \scriptsize \mid\; :5 \\[5pt]
8&=& x_1
\end{array}\)](https://mathjax.schullv.de/49c105fa854016f5c37f050c15bbb5e4c7fe4ce4c8df40a15e2c3e727d054ba6?color=5a5a5a)
![\(\begin{array}[t]{rll}
150+30x_2&=& 0&\quad \scriptsize \mid\; -30x_2\\[5pt]
150&=& -30x_2&\quad \scriptsize \mid\; :(-30) \\[5pt]
-5&=& x_2
\end{array}\)](https://mathjax.schullv.de/75ed5c7f000d48cc1f85e7f829220b354ee9822e209e9212a160d4a0d08f00a2?color=5a5a5a)
Da die beiden Nullstellen symmetrisch zur Symmetrieachse der Parabel liegen, verläuft diese durch die Mitte der Nullstellen:
Der Funktionswert an der Stelle 
folgt nun mit:
![\(\begin{array}[t]{rll}
y&=& (40-5\cdot 1,5)\cdot (150+30\cdot 1,5)& \\[5pt]
&=& 6337,5
\end{array}\)](https://mathjax.schullv.de/f519b0c661002c568dbf1c2d9700a888aa08efc6ae103fdf0808f3fc5efa93de?color=5a5a5a)
Der Scheitelpunkt ist somit der höchste Punkt der Parabel.
Wird der Preis also um pro Monat gesenkt, so werden mit einer monatlichen Gebühr von und Mitgliedern maximale Einnahmen von erzielt.
2
1. Schritt: Funktionsgleichung aufstellen
In Abhängigkeit von den Koordinaten des Punktes besitzt das Rechteck die Seitenlängen und 
Für den Flächeninhalt gilt also: 
Da der Punkt auf der Geraden liegt, gilt außerdem 
Einsetzen in die Gleichung für den Flächeninhalt liefert:
![\(\begin{array}[t]{rll}
A&=& x\cdot \left(-\dfrac{3}{2}x+3\right)& \\[5pt]
&=& -\dfrac{3}{2}x^2+3x
\end{array}\)](https://mathjax.schullv.de/1782aa523abd5e89462fd207f748a0c063344267a5ae9df8bc35cd462ce03bfb?color=5a5a5a)
2. Schritt: Nullstellen berechnen
Der Term 
wird genau dann null, wenn einer der beiden Faktoren null ist. Es folgt direkt 
Für den zweiten Term ergibt sich weiterhin:
![\(\begin{array}[t]{rll}
-\dfrac{3}{2}x_2+3&=& 0&\quad \scriptsize \,\bigg \vert \, \; +\dfrac{3}{2}x_2 \\[5pt]
3&=& \dfrac{3}{2}x_2 &\quad \scriptsize \,\bigg \vert \, \; : \dfrac{3}{2} \\[5pt]
2&=& x_2
\end{array}\)](https://mathjax.schullv.de/75cddd973c539b4678fc1954de2f98647fe4c9432f9dec17e02232e1abe25ec8?color=5a5a5a)
Die Symmetrieachse verläuft also durch 
3. Schritt: -Koordinate berechnen
An der Stelle 
gilt:
![\(\begin{array}[t]{rll}
y&=& -\dfrac{3}{2}\cdot 1+3 & \\[5pt]
&=& \dfrac{3}{2}
\end{array}\)](https://mathjax.schullv.de/915aa2535a5ddcf163b40cbdc46a9c49cc323c295869237140767e5a091003e1?color=5a5a5a)
Für die Koordinaten 
wird also der maximale Flächeninhalt von 
erreicht.