Boxplots
Aufbau
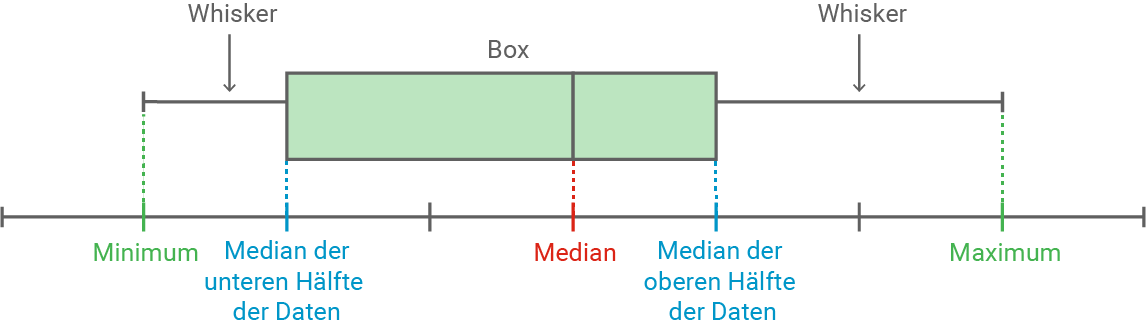
Ausreißer bei Boxplots
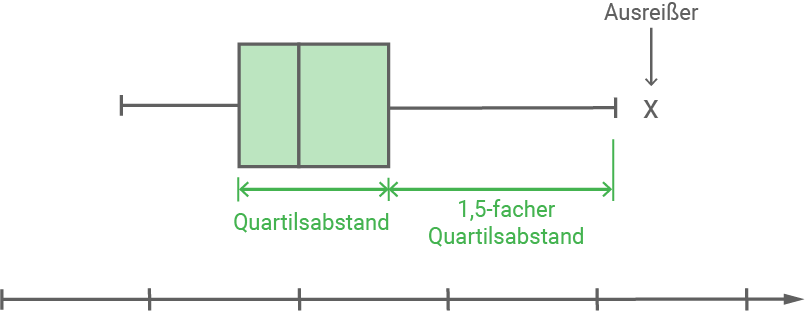
Datenpunkte, die deutlich außerhalb des Bereichs der übrigen Daten liegen, werden als Ausreißer bezeichnet.
Im Boxplot werden diese als einzelne Punkte jenseits der Whisker dargestellt. Die Whisker reichen dann nicht vom kleinsten bis zum größten Wert, sondern sind mit ihrer Länge auf das 1,5-fache des Quartilsabstandes beschränkt.
1
Lena und Hannah fahren jeden Tag mit dem Fahrrad in die Schule. Um herauszufinden, wer für den gleichen Schulweg länger braucht, notieren beide über einen Zeitraum von zwei Wochen jeden Tag ihre benötigte Zeit in Minuten:
Lena: 
Hannah: 
Stelle die Daten jeweils in einem Boxplot dar und vergleiche die benötigten Zeiten für den Schulweg.
2
Begründe oder widerlege die folgenden Aussagen anhand eines geeigneten Beispiels.
a)
Der Median liegt stets im Inneren der Box.
b)
Die Breite der Box im Boxplot ist direkt mit der Stichprobengröße verbunden.
c)
Wenn eine Datenreihe aus 50 Einträgen besteht, so muss die Breite der Box größer als null sein.
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
1. Schritt: Werte ordnen
Lena: 
Hannah: 
2. Schritt: Median ermitteln
Da beide Messreihen 10 Werte umfassen, entspricht der Median jeweils dem arithmetischen Mittel aus dem 5. und 6. Wert.
Für Lena gilt: 
Für Hannah gilt: 
3. Schritt: Median der oberen und unteren Hälfte bestimmen
Die untere Hälfte besteht aus den ersten 5 Werten und die obere Hälfte aus den letzten fünf Werten. Der Median der unteren Hälfte der Daten entspricht somit dem 3. Wert und der Median der oberen Hälfte dem 8. Wert.
Bei Lena entspricht der untere bzw. obere Median also 25 bzw. 40.
Bei Hannah entspricht der untere bzw. obere Median 18 bzw. 49.
Die Quartilsspannweite beträgt somit bei Lena 
und bei Hannah 
Bei beiden Datenreihen gibt es also keine Ausreißer, die über das 1,5-fache des jeweiligen Quartilsabstand hinausgehen.
4. Schritt: Boxplots zeichnen
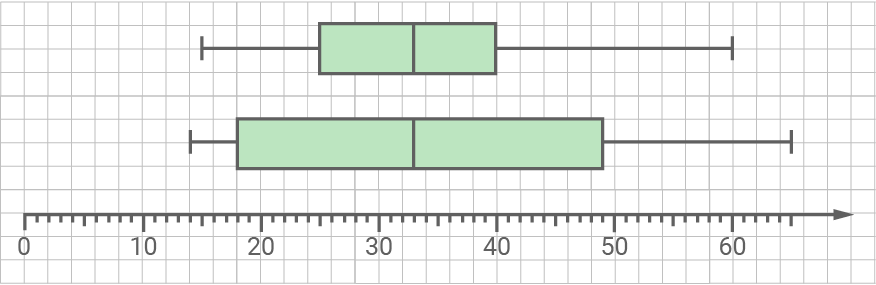5. Schritt: Boxplots vergleichen
Die Messwerte von Lena und Hannah stimmen in ihrem Median überein und sowohl die kürzeste als auch die längste benötigte Zeit für den Schulweg sind bei beiden ähnlich.
Bei Lena liegen jedoch die meisten gemessenen Zeiten näher am Median als bei Hannah.
Während Lena also meist eher ähnlich lange für den Schulweg braucht, schwanken die täglichen Fahrtzeiten bei Hannah stärker.
2
a)
Diese Aussage ist richtig.
Im Boxplot repräsentiert die Box den Bereich zwischen dem unteren und dem oberen Quartil und umfasst also die mittleren 
der Daten. Da der Median den mittleren Wert der geordneten Datenreihe darstellt und die Box vom ersten Viertel bis zum Dreiviertel der Daten reicht, liegt der Median folglich immer in der Box.
Beispiele, die dies bestätigen, sind die Boxplots aus Aufgabe 1.
b)
Diese Aussage ist falsch.
Die Breite der Box im Boxplot wird durch den Interquartilsbereich bestimmt, der die mittleren der Daten umfasst. Dieser hängt von der Streuung der Daten ab und hängt nicht direkt mit der Stichprobengröße zusammen.
Ein Beispiel sind die beiden Datenreihen 
und 
Trotz der gleichen Stichprobengröße von fünf Daten und identischem Median unterscheiden sich die jeweiligen Boxen in ihrer Breite. Die Box von 
reicht von 3 bis 7 und Box von 
von 4 bis 6.
c)
Diese Aussage ist falsch.
Die Breite der Box im Boxplot wird durch den Interquartilsbereich bestimmt, der von der Streuung der Daten abhängt. Stimmen das untere und obere Quartil miteinander überein, sind die Werte also alle identisch, so kann die Box eine Breite von null haben.
Würde beispielsweise 50 Mal eine Fahrtzeit von 20 Minuten für den Schulweg gemessen werden, dann würde die Box im Boxplot nur aus einer Linie bei dem Wert 50 bestehen und ihre Breite folglich null sein.