Quadratfunktion – Normalparabel
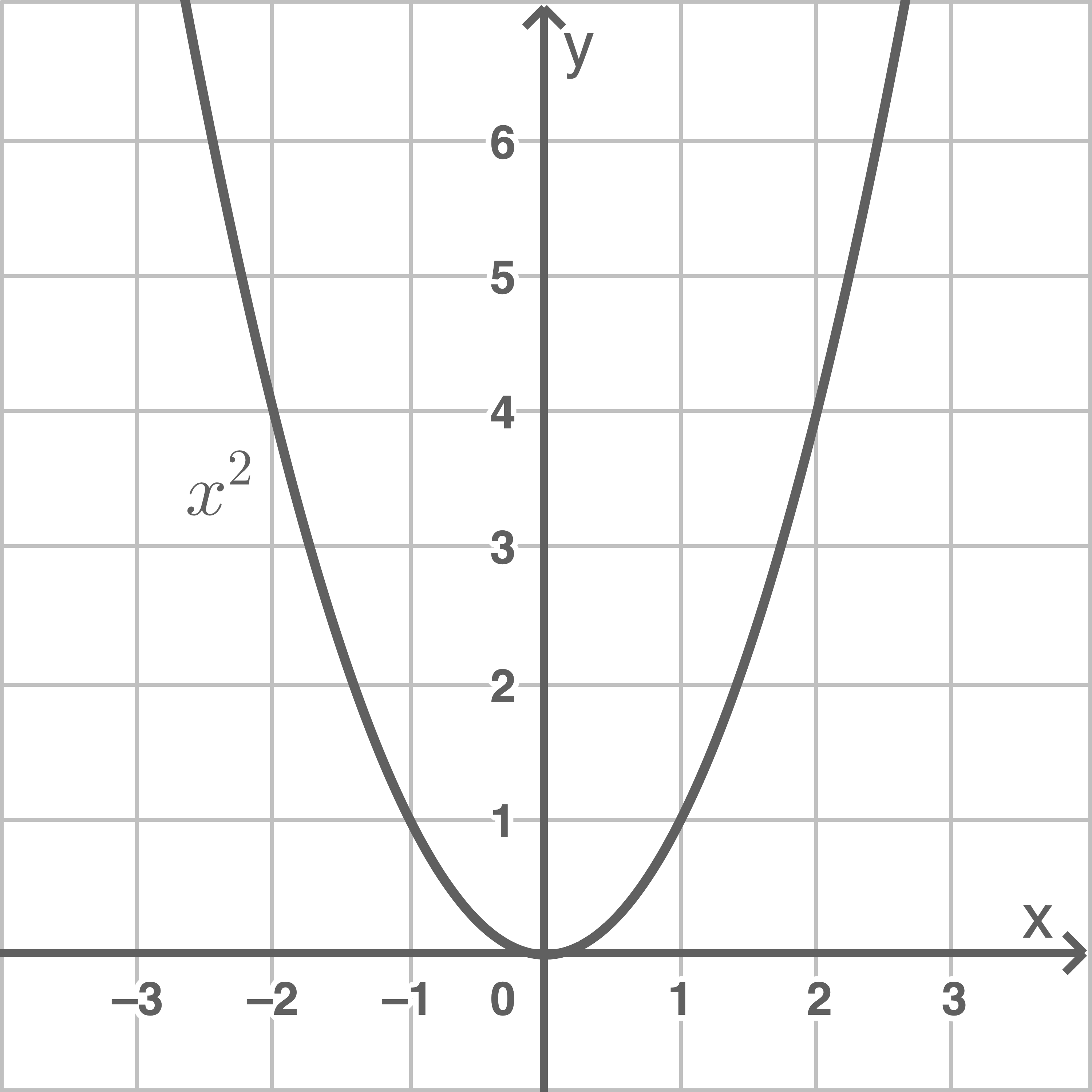
Der Graph der quadratischen Funktion 
mit 
heißt Normalparabel. Die Normalparabel
-Wert mit dem Faktor 
vervielfacht, so wird der zugehörige 
-Wert mit dem Faktor 
vervielfacht.
mit heißt Normalparabel. Die Normalparabel
- fällt für
- steigt für
- hat den Tiefpunkt
im Koordinatenursprung. Dieser Punkt wird Scheitelpunkt genannt. - ist symmetrisch zur -Achse.
-Wert mit dem Faktor vervielfacht, so wird der zugehörige -Wert mit dem Faktor vervielfacht.
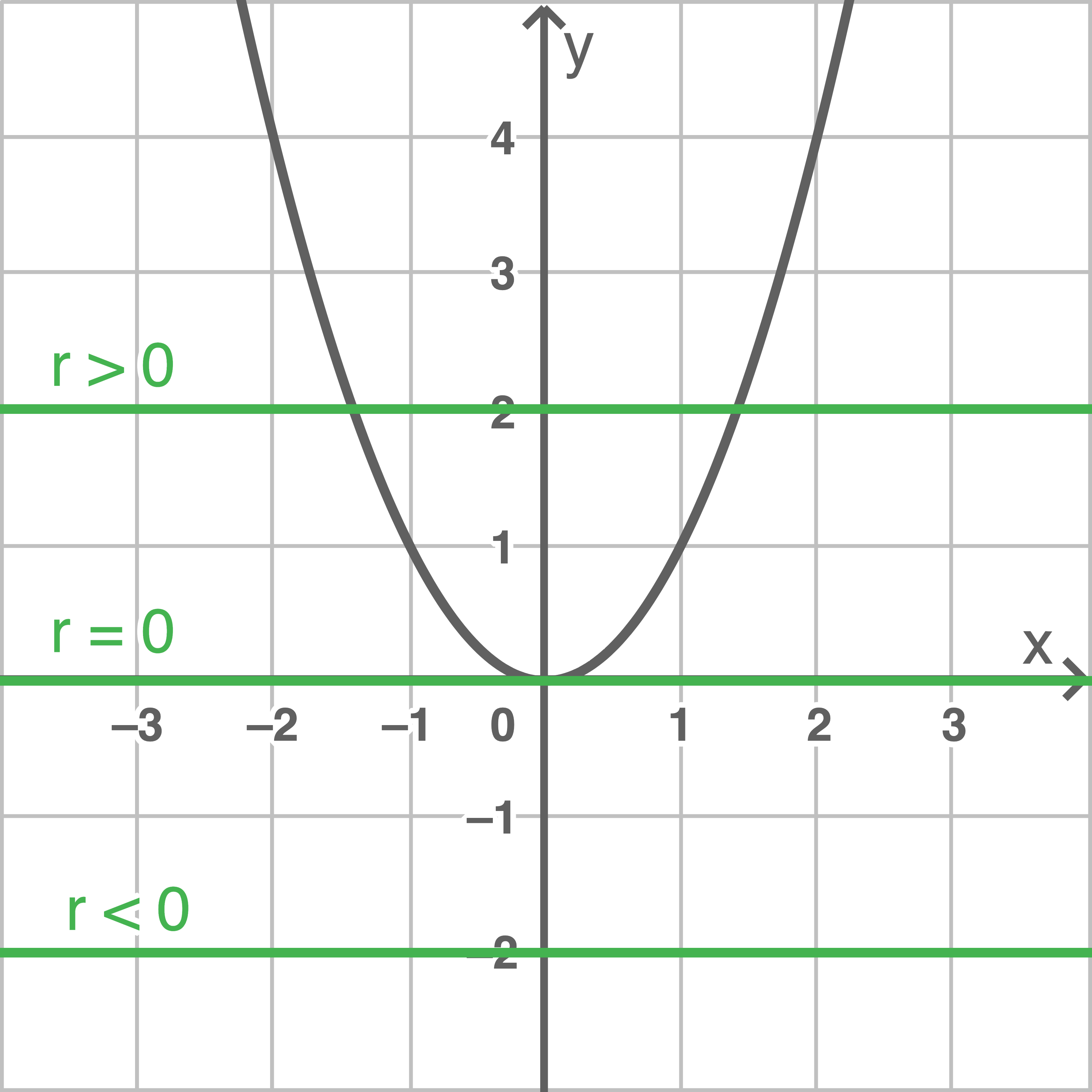
Grafisches Bestimmen der Lösungsmenge
Grafisch bedeutet das Lösen der Gleichung 
das Bestimmen der Schnittpunkte zwischen dem Graphen von 
und der Geraden 
Die Anzahl der Lösungen hängt vom Wert 
ab:
das Bestimmen der Schnittpunkte zwischen dem Graphen von und der Geraden
Die Anzahl der Lösungen hängt vom Wert ab:
Es gibt zwei Schnittpunkte, die Gleichung hat also zwei Lösungen.
Es gibt einen Schnittpunkt, die Gleichung hat die Lösung 
Es gibt keinen Schnittpunkt, die Gleichung hat also keine Lösung.
1
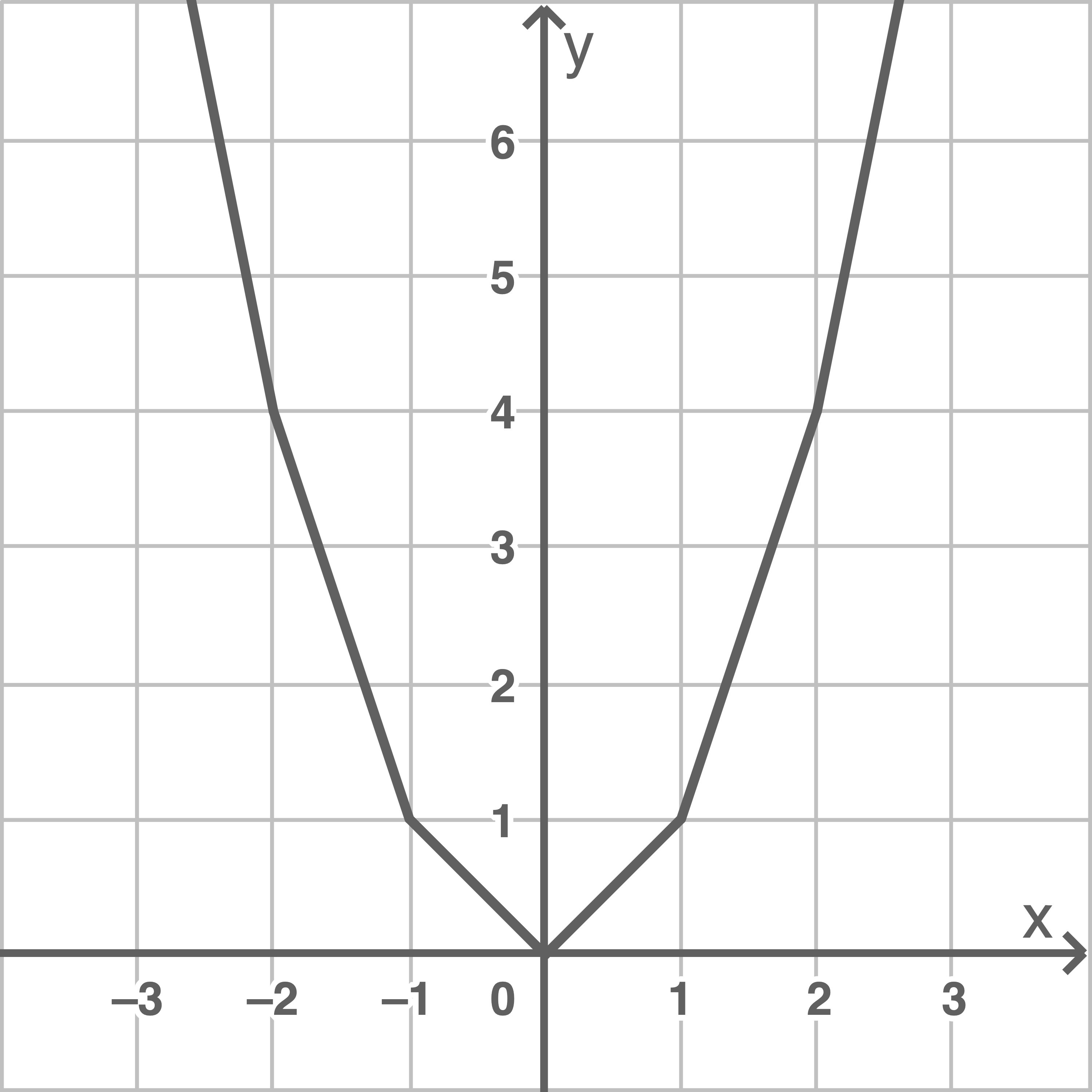
Erkläre, welcher Fehler beim Zeichnen der Normalparabel gemacht wurde und zeichne eine korrekte Normalparabel.
2
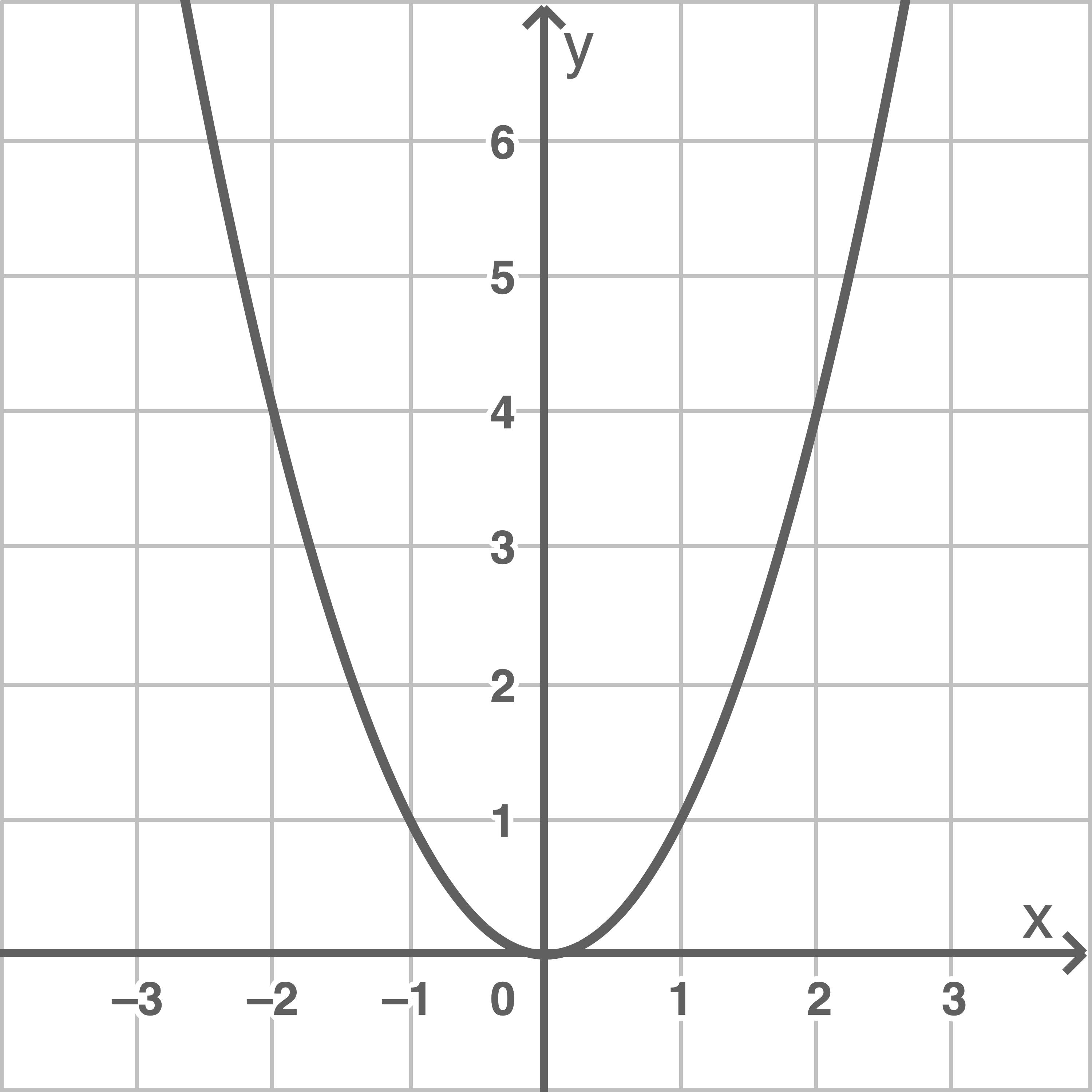
Gib an, wie viele Lösungen die quadratische Gleichung hat und bestimme diese.
a)
b)
c)
d)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
Die Punkte auf der Normalparabel wurden mit geraden Strecken verbunden. Eine Parabel ähnelt jedoch eher einer Kurve, daher müssen die Verbindungsstrecken gekrümmt sein.
2
a)
Wegen 
hat die quadratische Gleichung zwei Lösungen.
![\(\begin{array}[t]{rll}
x_1&=& 2 \\
x_2&=& -2
\end{array}\)](https://www.schullv.de/resources/formulas/3e6b39029e5e78eb2122da3a4c966a6fd17846805be12b704b1b17c1ed3f6bca_light.svg)
hat die quadratische Gleichung zwei Lösungen.
b)
Wegen 
hat die quadratische Gleichung keine Lösung.
hat die quadratische Gleichung keine Lösung.
c)
Wegen 
hat die quadratische Gleichung zwei Lösungen.
![\(\begin{array}[t]{rll}
x_1&=& 1,5 \\
x_2&=& -1,5
\end{array}\)](https://www.schullv.de/resources/formulas/0d3789703fa2ace957f01b5518c614553122daaf365737959a3ab4622e64cd44_light.svg)
hat die quadratische Gleichung zwei Lösungen.
d)
Wegen 
hat die quadratische Gleichung die Lösung
hat die quadratische Gleichung die Lösung