Bestimmen von Werten für Sinus, Kosinus und Tangens
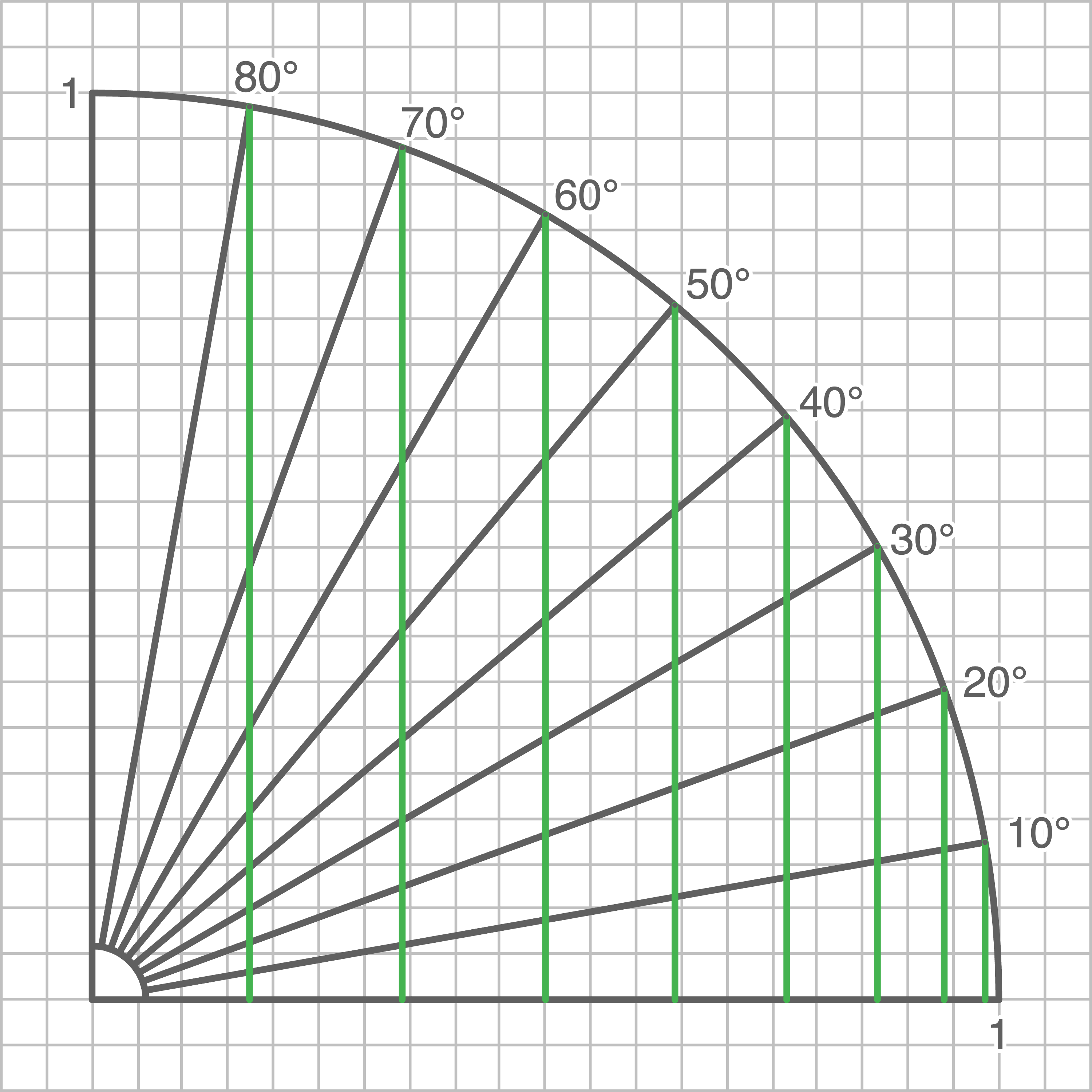
Zeichnerische Bestimmung von Näherungswerten
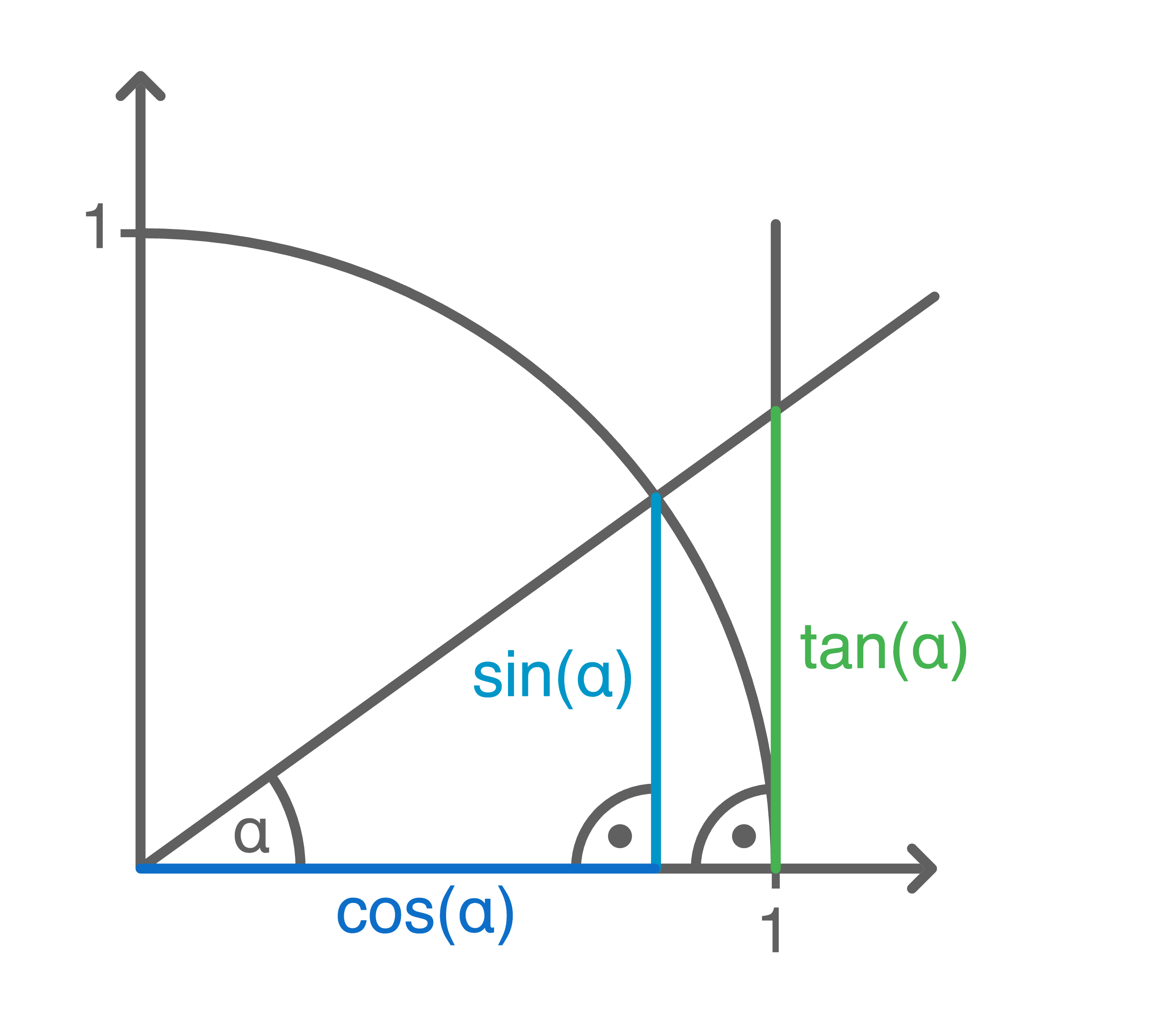
Der Einheitskreis ist der Kreis um den Koordinatenursprung  mit dem Radius 1. Die Werte und Eigenschaften für Sinus, Kosinus und Tangens können durch Einzeichnen eines Viertels des Einheitskreises sowie verschiedener rechtwinkliger Dreiecke mit den Winkelgrößen
mit dem Radius 1. Die Werte und Eigenschaften für Sinus, Kosinus und Tangens können durch Einzeichnen eines Viertels des Einheitskreises sowie verschiedener rechtwinkliger Dreiecke mit den Winkelgrößen  am Kreismittelpunkt bestimmt werden.
Die Hypotenuse entspricht hierbei jeweils dem Kreisradius. Durch Messen der jeweiligen Ankathete und Gegenkathete können folgende Werte berechnet werden:
am Kreismittelpunkt bestimmt werden.
Die Hypotenuse entspricht hierbei jeweils dem Kreisradius. Durch Messen der jeweiligen Ankathete und Gegenkathete können folgende Werte berechnet werden:
Beziehungen zwischen Sinus, Kosinus und Tangens
Für
a)
b)
c)
d)
1
Zeichne ein geeignetes rechtwinkliges Dreieck und berechne jeweils Sinus, Kosinus und Tangens für:



a)
b)
c)
2
a)
Bestimme mit dem Taschenrechner die Werte für Sinus, Kosinus und Tangens mit folgenden Werten von 
Was fällt auf?
b)
Bestimme mit dem Taschenrechner die Werte für Sinus, Kosinus und Tangens mit folgenden Werten von 
Was fällt auf?
c)
Vergleiche  und
und  für die folgenden Werte von
für die folgenden Werte von 
Was fällt auf? Erkläre die Beobachtung am Einheitskreis.
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
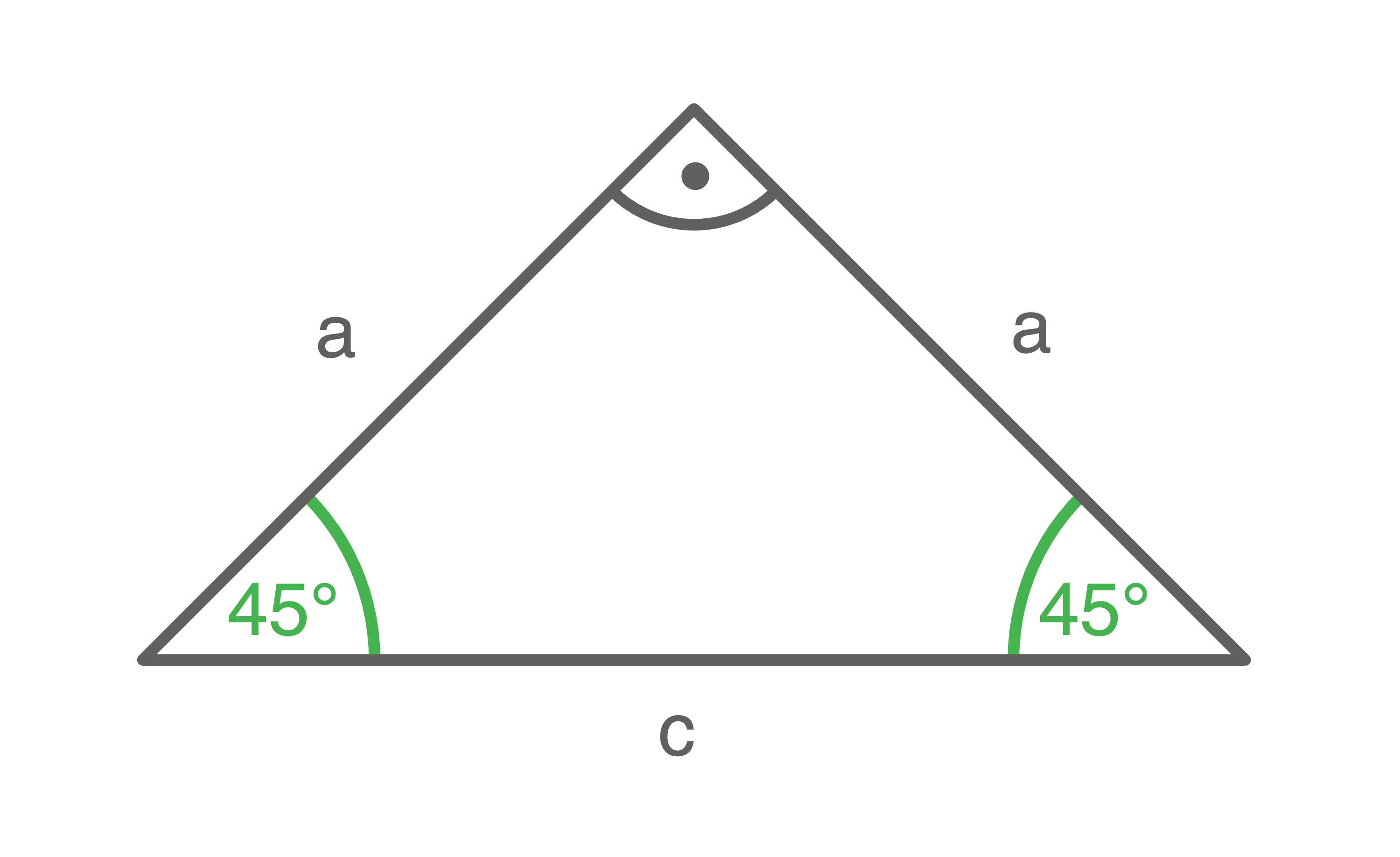
a)
Da das Dreieck einen rechten Winkel sowie einen Winkel von  besitzen soll, folgt für den übrigen Winkel
besitzen soll, folgt für den übrigen Winkel 
 Das Dreieck ist somit gleichschenklig mit der Schenkellänge
Das Dreieck ist somit gleichschenklig mit der Schenkellänge  Für die Hypotenuse
Für die Hypotenuse  folgt mit dem Satz des Pythagoras:
folgt mit dem Satz des Pythagoras:
![\(\begin{array}[t]{rll}
c^2&=& a^2+b^2 & \quad \scriptsize \mid\;b=a \\[5pt]
c^2&=& 2a^2 &\quad \scriptsize \mid\; \sqrt{\,}\\[5pt]
c&=& \sqrt{2}a
\end{array}\)](https://www.schullv.de/resources/formulas/a1efabc380128944d203014d56c8ed1d0bcb55a4e72df65c8365dbb205dfbe60_light.svg) Damit ergibt sich:
Damit ergibt sich:
![\(\begin{array}[t]{rll}
\sin(45^\circ)&=& \dfrac{a}{c}& \\[5pt]
&=& \dfrac{a}{\sqrt{2}a}&\\[5pt]
&=&\dfrac{1}{\sqrt{2}} &\quad \scriptsize \,\bigg \vert \, \; \cdot \dfrac{\sqrt{2}}{\sqrt{2}} \\[5pt]
&=& \dfrac{1\cdot \sqrt{2}}{\sqrt{2}\cdot \sqrt{2}}& \\[5pt]
&=& \dfrac{1}{2} \sqrt{2}
\end{array}\)](https://www.schullv.de/resources/formulas/0ba92632d800677f03b317b15b519053d2e5a5ffe3e51c3f080cfc7a3a3b7d14_light.svg) Aufgrund der Gleichschenkligkeit gilt:
Aufgrund der Gleichschenkligkeit gilt:
 Außerdem ergibt sich:
Außerdem ergibt sich:

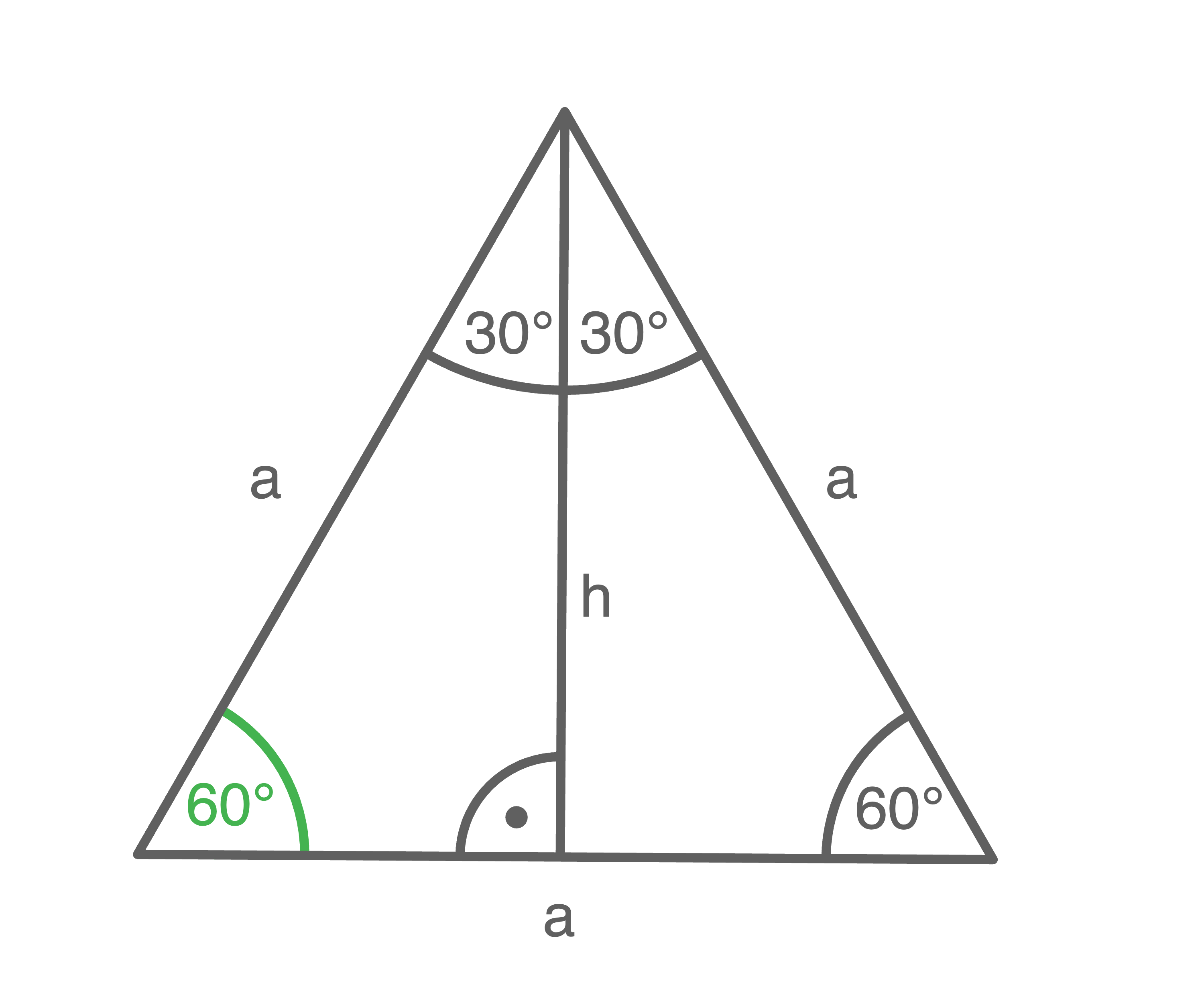
b)
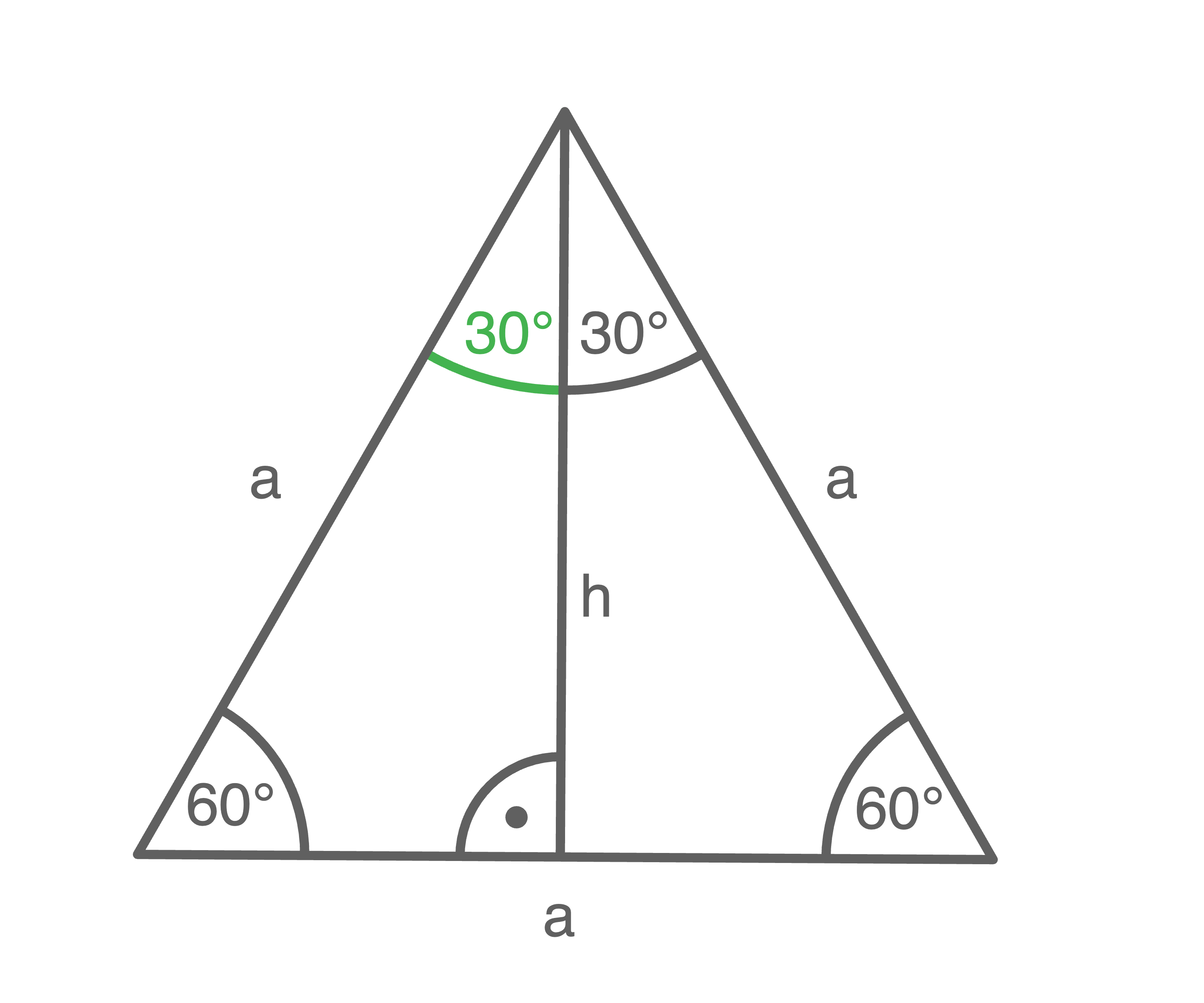
In jedem gleichseitigen Dreieck sind alle Winkel  groß. Die Höhe einer Seite
groß. Die Höhe einer Seite  halbiert hierbei das gleichseitige Dreieck mit dem gegenüberliegenden Winkel in zwei rechtwinklige Dreiecke mit den Winkelgrößen
halbiert hierbei das gleichseitige Dreieck mit dem gegenüberliegenden Winkel in zwei rechtwinklige Dreiecke mit den Winkelgrößen  und
und  .
Die Höhe
.
Die Höhe  entspricht nun der Gegenkathete und ergibt sich mit dem Satz des Pythagoras zu:
entspricht nun der Gegenkathete und ergibt sich mit dem Satz des Pythagoras zu:
![\(\begin{array}[t]{rll}
a^2&=& h^2+\left(\dfrac{a}{2}\right)^2 &\quad \scriptsize \,\bigg \vert \, \; -\left(\dfrac{a}{2}\right)^2 \\[5pt]
a^2 -\left(\dfrac{a}{2}\right)^2 &=& h^2 & \\[5pt]
\dfrac{4a^2}{4} -\dfrac{a^2}{4} &=& h^2 & \\[5pt]
\dfrac{3}{4}\cdot a^2 &=& h^2 &\quad \scriptsize \,\bigg \vert \, \;\sqrt{\;} \\[5pt]
\dfrac{\sqrt{3}}{\sqrt{4}}\cdot a &=& h &\ \\[5pt]
\dfrac{a}{2}\sqrt{3}&=& h
\end{array}\)](https://www.schullv.de/resources/formulas/aa17519cfa4c4ea30f33bcb35abf537c98ac25737eff9c7eb5befa039a7a7e98_light.svg) Damit ergeben sich:
Damit ergeben sich:



c)
Analog zu Aufgabenteil b) ergibt sich mit der Höhe  und dem Winkel
und dem Winkel 
![\(\begin{array}[t]{rll}
\sin(30^\circ)&=& \cos(90^\circ-30^\circ)& \\[5pt]
&=& \cos(60^\circ )& \\[5pt]
&=& \dfrac{1}{2}
\end{array}\)](https://www.schullv.de/resources/formulas/d0e1556a5b5034f51e4bb4c05ace7e05e043d0fa018ce2c4d41cf38ab8d2f4d1_light.svg)
![\(\begin{array}[t]{rll}
\cos(30^\circ)&=& \sin(90^\circ-30^\circ) & \\[5pt]
&=& \sin(60^\circ)& \\[5pt]
&=& \dfrac{1}{2}\sqrt{3}
\end{array}\)](https://www.schullv.de/resources/formulas/85591250855a128350e7d1f87734a7464b2e2a0dcc5b775243a798fdb091dbc0_light.svg)
![\(\begin{array}[t]{rll}
\tan(30^\circ)&=& \dfrac{\frac{a}{2}}{h}& \\[5pt]
&=& \dfrac{\frac{a}{2}}{\frac{a}{2}\sqrt{3}} & \\[5pt]
&=& \dfrac{1}{\sqrt{3}}&\quad \scriptsize \,\bigg \vert \,\; \cdot \dfrac{\sqrt{3}}{\sqrt{3}}\\[5pt]
&=& \dfrac{1\cdot \sqrt{3}}{\sqrt{3}\cdot \sqrt{3}}& \\[5pt]
&=&\dfrac{1}{3}\sqrt{3}
\end{array}\)](https://www.schullv.de/resources/formulas/009d5d41e4ffcdf9d1df206853344a04147e369356c166b7ae3445ea3289129b_light.svg)
2
a)
b)
c)